基于散乱点云的飞机蒙皮缝隙识别算法

李红卫，戴佳佳，谢 乾，汪 俊+

(1.航空工业西安飞机工业(集团)有限责任公司，陕西 西安 710089； 2.南京航空航天大学 机电学院，江苏 南京 210016)

0 引 言

随着飞机制造向智能制造方向发展的趋势，高精度的数字化测量技术在飞机制造领域得到广泛的应用[1,2]，是飞机制造过程中的关键技术之一。飞机蒙皮是飞机气动外形及承力、传力结构体系的重要组成部分[2]。该类零件具有厚度薄、刚度弱、易变形、尺寸大[2]等结构特征。蒙皮通过铆接、螺接等形式与飞机机体骨架连接，由于装配过程中铆钉的应力作用，导致蒙皮缝隙的测量结果与设计不相符，这是对飞机飞行性能影响较大的关键因素之一[3]，因此对于蒙皮接缝的识别是机身自动化检测的基础和必要步骤。

目前对于蒙皮缝隙的检测多采用手持非接触式设备进行测量，而缝隙识别仍采用人工辨别。但随着机器人技术的快速发展，机械臂等机器人设备能够进行部分重复性工序，有效减少人力的消耗，在制造领域得到广泛的应用。结合机械臂的检测过程中，针对检测目标的自动化识别是必不可少的步骤之一，对于蒙皮缝隙的识别是飞机机身智能化检测的重要前提。

本文结合机械臂与三维激光扫描设备，研究飞机蒙皮特征提取和对缝识别等内容。主要创新点在于提出基于散乱点云的蒙皮对缝识别方法，研究点云的内在几何规律，设计三维点云的张量投票方法以及强化决策机制的多直线拟合算法，高效解决飞机蒙皮对缝自动化识别的效率问题。

1 相关工作

近几年相关检测技术在我国航空制造业进行了一定的研究与探索，也取得了一定的成绩，大多采用非接触式测量方式。根据采用设备的不同，已有的非接触式测量又分为基于线结构光的方法和基于三维扫描仪的方法。

余飞翔等将飞机缝隙特征视作为蒙皮的边缘特征进行提取，利用邻域搜索方法进行曲率信息的计算，从而识别测量点，并进一步拟合直线[3]。许大帅和杜福洲结合结构光视觉技术和iGPS测量系统实现了阶差间隙的实时动态测量，在线结构光测量设备进行飞机蒙皮对缝测量的同时，iGPS跟踪测量的位置，并将测量结果和位置信息转换为全局坐标系中，实现飞机蒙皮对缝的动态测量[4]。

严成等开发了基于三维点云的缝隙测量系统，通过激光设备获取蒙皮对缝点云数据，构建蒙皮对缝间隙、阶差的数学模型[2]。陈松林等利用光栅投影技术同时获取散乱点云和二维图像，在图像上提取对缝区域，根据二维图像与三维点云之间的对应关系，将图像上的对缝区域定位到三维点云上，从而实现三维点云的对缝区域提取，并进一步实现三维空间中间隙阶差的测量[5]。张洪瑶等提出一套飞机蒙皮自动化检测系统，通过机器人和三维激光扫描仪的结合，对飞机蒙皮模型对缝间隙与阶差测量方法进行深入研究，建立了对缝的缝宽与阶差的数学模型，实现飞机蒙皮对缝区域的自动定位、检测和分析，实现对缝的高效率、高精度的自动化检测与分析[6]。

国外对于蒙皮接缝测量技术的研究已进入实际工程应用阶段，配套研发相应的间隙测量设备，受到测量领域的大量推广和应用，其中包括飞机装配检测的应用，一定程度上提高飞行器的生产效率与制造精度。国外的相关研究已与产业相结合，生产了专业的数字化测量设备用于对缝间隙和阶差的测量[7,8]，例如英国Third Dimension Software公司的激光间隙枪GapGun应用在汽车制造行业，测量车身的间隙；加拿大LMI Technologies公司的线激光轮廓传感器Gocator系列产品使用投影激光线进行高分辨率扫描、测量和控制，美国LAP公司生产的ANTARIS系列产品多应用在工业制造中。这类产品通常是手持的方式进行测量，虽然测量结果准确，但是单次测量只能得到一次测量数据，存在测量的局限。

现有的研究以及已成型的测量设备，多采用线结构光的检测模式，而线结构光通常一次只能从一个角度采集一次数据进行接缝间隙和阶差的测量计算，计算速度较快、精度较高，但对于飞机蒙皮接缝来说，因飞机机体尺寸大、刚度小、易变形，单次的蒙皮接缝测量数据的具有一定的“偶然性”，测量结果往往不能作为最终的测量结果，而同时人工手持设备进行测量的方式则提高了人力成本和时间消耗，在一定程度上不能满足生产需求。本文针对效率问题，提出利用三维点云进行蒙皮接缝检测，能够一定程度上减少测量数据的“偶然性”，提高后续蒙皮对缝检测效率。

2 算法概述

本文结合机械臂和三维扫描仪设备，对飞机蒙皮零件分别进行扫描，并通过三维点云数据采集、特征提取、建模分析等技术处理，实现快速、精准的对缝自动化、智能化识别，提升飞机蒙皮对缝检测的技术能力。

本文的目标是从原始点云数据中识别缝隙点。通过三维扫描仪设备扫描捕获的真实点云数据中，仅有一小部分点能够作为有效的缝隙区域点云，大部分数据点为噪声和离群点[2]，针对大量的噪声点和离群点，本文首先分析散乱点云的数据分布，运用点云数据的几何信息构造点云张量，并通过邻近点进行张量投票，随后利用张量分解后的显著性值进行对缝区域的提取。这样的对缝区域中仍存在少量离群点，且这些离群点与缝隙点十分相近，两者之间的相似度较高，对这类离群点的排除具有较大的技术难度。

为进一步识别精细的缝隙点，本文采用多模型拟合的方法对接缝区域的点集进行多直线拟合。将拟合直线上的点视为对缝点，其余点均视为离群点。同时针对多条直线，还需考虑伪离群点对拟合过程的影响。本文算法基于迭代的方法逐步拟合直线，并结合强化决策机制实现优化拟合的结果。

具体流程如图1所示。

3 算 法

本文利用机械臂搭载扫描设备进行飞机蒙皮数据的采集。原始点云数据往往包含大量孤立点，可能会对本文的算法产生一定的影响，前期预处理主要采用双边滤波的方法，删除这些孤立点。同时结合k-邻近算法和PCA主成分分析法计算点云数据的法向量，以便为后面的识别算法提供更丰富的几何信息。下面详细介绍本文的算法内容。

3.1 缝隙区域提取

根据本文的研究目标，定义蒙皮表面缝隙点所在区域为对缝区域，除此之外的区域为非对缝区域。对缝区域主要由缝隙点与少量离群点组成，非对缝区域的数据点均为离群点。其中仅有一小部分点能够标记为有效的对缝区域。本文首先通过分析散乱点云的数据分布，结合点云的几何信息构造点云张量，并利用张量投票和张量分解后的显著性值构造阈值进行对缝区域的提取。

3.1.1 张量投票原理

张量投票理论是一种计算机视觉和机器学习的感知编码法，对噪声数据具有较强的鲁棒性，通过各点的张量及其邻近点的信息传递来提取数据中隐含的几何结构[9]，近年来被广泛应用在三维数据特征提取中。张量投票算法[9]主要由张量描述、张量投票及张量分解3部分组成。主要是利用三维数据的几何信息构造的各离散点的张量矩阵，随后通过该矩阵向周围的邻近点进行信息投票。投票完成后，每个离散点都记录着从邻近点所获取的几何信息。这些几何信息使得张量投票理论能够进行数据结构特征的推理。

本文提出一种基于张量投票的三维点云对缝特征标定方法。该方法充分利用原始点云数据中含有的几何信息，计算各点的张量，每个张量都编码各点与其相邻点之间的基本几何信息；随后进行投票并分解获取特征值，并设定阈值，根据特征值与设定阈值之间的比较进行三维点云的对缝区域标定。

3.1.2 对缝区域标定

定义输入数据为离散点云P，对于P中的任意一点pi(x,y,z)， 获取点pi的k邻近点集N(pi)。 计算各点的张量，由邻近点pj对点pi进行投票，定义投票结果为Ti，公式[9]如下

Ti=∑ci(I3-(rTei)2)

(1)

通过张量投票计算Ti，然后利用式(2)获得其特征值

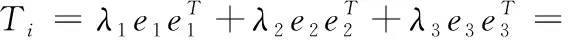
(2)

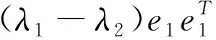
根据三维的椭圆球来解析张量分解后的3个分量，如图2所示，其中棒张量分量由e1构成，对应空间平面法向，其显著性值(λ1-λ2)代表点pi所属平面的倾向度；板张量分量由e1e2构成，对应空间直线的切向，其显著性值(λ2-λ3)表示该点所属直线的倾向度；e1e2e3构成球张量分量，对应角点，其显著性值λ3表示所属角点的倾向度。设定阈值ε针对显著性值进行过滤，具体公式如下

(3)

图2 张量分解对应的椭圆球

将ωi设为各点的权值，结合实际点云数据权值的分布与式(3)，设置阈值ε，权值大于等于阈值的点定义为对缝区域的点，反之则该点隶属于非对缝区域，即为离群点。其中阈值的设置主要根据实际数据张量投票的计算结果。

张量投票能够在存在严重噪声的情况下快速的检测出特征点，能够获得蒙皮点云数据中点集的局部固有结构。因此，通过张量投票算法，能够获得了含有对缝结构的局部点云数据。但是由于点云数据的不均匀分布特点，该局部点云中仍然存在少量的离群点，如图3所示，其中虚线框中均为离群点，椭圆中表示对缝形状中也存在部分离群点。接下来需要进一步精细精准提取对缝点。

图3 含有对缝形状的缝隙区域

3.2 缝隙点识别

通过上述技术处理，我们利用原始点云数据内在几何属性能够捕获缝隙的形状特征。为了尽可能多地获得精确识别的有效判断信息，从张量投票中捕获的点来进行缝隙点的识别分类，根据同一类别的缝隙点即隶属于一条直线的几何属性，结合多模型拟合方法进行多条直线的拟合，以此精确识别缝隙点。

3.2.1 对缝点定义

通过提取缝隙区域，可以有效降低其它区域点集对缝隙点识别过程的影响，能够获得较为准确的缝隙点。上述方法获得的对缝区域包含内点所属的对缝形状的直线部分，以及少量的离群点。对缝形状由待识别的缝隙点组成，为准确识别这些缝隙点，分析对缝形状的几何属性，缝隙点之间隶属于同一条直线的概率较大，且至少需要进行两条直线的拟合，因此对缝直线拟合可视为多模型拟合问题。

当数据中存在多个模型时，针对当前指定的模型，其它模型的内点虽然不属于离群点，但因不符合当前模型的分布规律，被称之为当前模型的伪离群点[10]，如图3所示。伪离群点与离群点同样对特定模型具有一定程度的干扰性，增加了缝隙点精确识别的难度。

3.2.2 基于强化决策的识别

本文采用一种强化决策机制进行多模型拟合[11]。模型变量的选择可以看作是一个决策，多模型的拟合是由一系列决策组成的过程，通过奖励机制可以有效地优化决策过程。

设D∈3为对缝特征点集，特征直线拟合的目标是找到一个最相似的直线模型，且对缝形状中至少包含两条对缝特征直线，因此至少需要拟合两条直线，设M为多模型的并集，即M=∪i=1nMgθi， 其中n为拟合模型的总个数，Mgθ是由给定的参数规则g定义的模型，而参数规则g由变量θ获得。特征直线拟合算法主要步骤如下：

(1)初始化：设置参数的初值，包括拟合模型总个数n，随机初始化变量 (θ1*,θ2*,…,θn*)， 迭代次数itermax；

(2)迭代判断：若迭代次数iter≤itermax则重复步骤(3)至步骤(6)；

(3)单模型拟合：若i

(4)随机选点：随机选择2个点，计算该直线参数f(x,y,z)；

(6)参数更新：当内点个数发生变化，即Num(q(1),q(2),…,q(n))>Num(θ1*,θ2*,…,θn*)， 当前计算获得的内点的个数大于上一次迭代的变量的个数，则 (θ1*,θ2*,…,θn*)=(q(1),q(2),…,q(n)) 更新内点数。

由于对缝区域点云所属两条直线的间隙较小，非常容易将两条直线拟合为一条直线，因此本文采用迭代的形式逐步排除离群点。在拟合一条直线后，计算各点到该条直线的距离，根据距离值设定阈值进一步区分离群点和内点，距离值小于设定阈值的点为内点，反之则为离群点。随后抛出属于该直线的内点，利用余下的点进行下一条直线的拟合。以此循环迭代，直至最终拟合直线的个数达到预设值。

4 实验分析

为验证本文算法的可靠性和有效性，本文进行了飞机蒙皮对缝直线识别实验。首先通过机械臂持高精度扫描仪在飞机的缝隙区域进行扫描操作，得到真实的点云，图4展示了UR机械臂持扫描仪在飞机模型表面获取的蒙皮对缝的真实数据。其中图4中使用的机械臂负重为5 kg。从图4中点云数据的分布可直观判断，对缝区域的点具有较为明显的线条特征，将该数据作为本文算法的输入，进行对缝直线特征的自动识别，以此来验证本文算法对散乱点云数据的可实施性。

图4 蒙皮缝隙与真实扫描点云数据 注：图4中的飞机为飞机模型，并非真实的飞机

针对同一项扫描任务，若采用人工手持扫描仪进行数据采集，则至少需要安排2名～3名人员来进行这一步骤，需要花费时间约为30 min，其中由于人工扫描的不便，工作人员需要全程高度参与扫描过程；而采用机械臂持扫描仪采集数据则最多只需要1人即可，前期扫描路径的规划算法由本项目组其它人员进行开发，加载该算法耗时较短(1 s之内)可忽略不计，机械臂扫描所需时间约为20 min，但是在机械臂扫描过程中，并不需要工作人员的高度参与，工作人员只需在后端监控扫描数据是否完整即可，也可以同时做其它的任务。相较于人工手持的扫描方式，通过机械臂采集数据的方式明显较少了人力的消耗，时间上也能并行作业。

4.1 缝隙区域提取结果

散乱点云的缝隙区域的提取过程如图5所示，根据点云张量计算方法计算输入点云的张量，并进行张量投票和张量分解，将获得的显著性值根据式(3)计算得到该点的权值。

图5 散乱点云对缝区域提取过程

如图5所示，将各点的权值转化为该点的灰度值进行可视化显示，颜色从白色到黑色分别表示权值从0到1的变化趋势，点的颜色越深说明该点的权值越大。同时点的权值分布图右边的条状图为不同颜色对应的点个数的分布结果。如图5(a)所示，将各点的显著性值直接相加的结果赋为各点的权值，并进行归一化操作，图5(c)为利用式(3)计算的本文的权值的分布结果。对比图5(a)与图5(c)，图5(c)中灰色的区域明显大于图5(a)中的灰色区域，且图5(a)右侧的条状图中点多数分布在中间区域，而图5(c)右侧的条状图表明点的分布靠近白色，同时图5(c)中对缝区域要略小于图5(a)中的对缝区域，大部分的非对缝区域点的权值要小于对缝区域点的权值。对缝区域的收缩有利于标记对缝区域的点，具体标记结果如图5(b)和图5(d)所示。图5(b)为根据图5(a)中的权值进行对缝区域提取的结果，图5(d)为根据图5(c)中的权值进行对缝区域提取的结果，对比图5(b)和图5(d)，图5(b)中的提取结果含有较多的离群点。视觉上直观对比图5(c)与图5(d)，可确认对缝区域提取这一操作已经排除了大量的噪声和离群点。

4.2 缝隙点识别结果

缝隙点识别过程如图6所示，运用多模型拟合算法进行缝隙点的准确识别。图6(a)为输入的原始点云数据，图6(b)为对通过张量投票计算之后的图6(a)的缝隙区域的识别结果，并将该结果作为模型拟合的输入，逐步迭代优化来判断各直线的所属内点，并根据最小二乘拟合直线，计算归于同一条直线的模型参数。如图6(c)所示，将识别的缝隙点拟合后的黑色直线表示为识别结果，同时具体的直线量化结果见表1。

图6 对缝识别过程

由于本文中采用的数据为三维扫描仪获取的飞机蒙皮缝隙处的真实散乱点云，缝隙点没有对应的人工标注。但是由于缝隙点在飞机蒙皮上均隶属于缝隙直线，可以根据缝隙点与缝隙直线的关联特征来评判缝隙点的识别结果。因此本文引入直线度[12]的概念来评定拟合直线的精度，具体公式[12]如下

直线度=max(Δi)-min(Δi)

(4)

其中，Δi为缝隙点到直线的距离，空间直线的点向式方程[13]为

(5)

其中，m,n,p为拟合直线在各方向上的系数，x0,y0,z0为该直线上的已知点。

表1 对缝直线拟合精度

如图7所示，针对同一点云数据，本文方法与文献[14]提出基于Hough变换的直线检测算法进行对比。其中图7(b)与图7(c)分别为基于Hough变换方法的直线检测结果和拟合直线的结果。从图中可以看出，该方法虽然能够检测对缝直线，但是同时也相应的有一定的误检测结果，且误检结果会严重干扰对缝直线的识别。对比文献[14]，本文的识别结果不存在明显的误检，能够清晰识别对缝直线。

利用所有被识别为缝隙点的点集进行直线的拟合，并计算直线度。若直线度越大，则表明该直线上存在某一点距离该直线较远，而根据缝隙点隶属于同一条直线的属性，距离拟合直线较远的点不应该是缝隙点，由此可进行缝隙点识别结果的判定，因此直线度越小，识别结果越好。针对上述拟合的两条直线进行精度评定，具体如表1所示。获得的拟合直线参数与空间直线点向式方程参数一致，说明本文拟合直线的正确性与可靠性，直线1和直线2的内点个数分别为166和153，而基于Hough变换直线检测提取的内点数为156和146，均低于本文方法识别的点个数。根据式(4)计算两条直线的直线度，表1中两直线的直线度较小，直线度越小，说明各个缝隙点越接近于拟合直线。本文方法计算的直线度均低于基于Hough变换方法得到的直线的直线度。

图7 本文与文献[14]的结果对比

5 结束语

本文提出了一种基于散乱点云的飞机蒙皮对缝识别算法，针对机器人与三维扫描设备获取的飞机蒙皮散乱点云数据，引入张量投票理论，充分利用点云数据的内在几何信息，快速剔除大量噪声点和离群点，随后进行缝隙点的精准识别，建立对缝直线方程，为飞机蒙皮缝隙点的识别计算构建数学模型，再进一步根据模型进行飞机蒙皮对缝的直线拟合。实验结果表明，本文提出的方法能够实现一次测量完成三维扫描区域飞机蒙皮所有对缝的自动定位和高效率、高精度的自动识别与提取。