正则化HSS预处理鞍点矩阵的多尺度算法

董朝丽，汪钰斌

(江西农业大学南昌商学院，江西 共青城 332020)

1 引言

在众多重要领域，例如计算流体力学、电磁场推算及对众多偏微分方程的有限差分与有限元离散中，均会生成大规模的线性方程组[1]。鞍点问题作为一种特殊的线性方程组，在线性弹力学、图像处理等科学研究中拥有极为广泛的应用[2]。

近年来，相关研究学者对种类繁多的鞍点求解问题进行了不同方面的研究，并给出很多行之有效的求解方法。曹阳等[3]提出正则化HSS预处理鞍点矩阵的特征值估计，分析复特征值及实特征值的上下边界，并以特征值均为实数作为充分条件，最终证明该方法测得的复特征值更精确。董贝贝等[4]提出求解鞍点问题的广义正定和反Hermitian分裂方法，利用矩阵的正定分裂构造鞍点矩阵的两种分裂格式，结合迭代收敛充要条件，利用分裂格式构造算法迭代。刘李楠等[5]提出基于超松弛预处理的精细积迭代反演算法，将方程组求解归结为初值问题的极限形式，利用超松弛法预处理正演所得鞍点矩阵，降低条件数以减少测量扰动对反演计算的影响。鞍点系统中系统矩阵对角块具有奇异性，在系数矩阵阶数较大的情况下，受到计算机CPU、内存与偏差等众多外界因素干扰，上述的某些鞍点求解方法就不能给予较为准确的收敛解。

为了完善鞍点问题的计算收敛速度，减少计算机CPU占用率，使计算结果更加精准，本文提出一种正则化HSS(Regularrized Hermitian and skew-Hermitian splitting，RHSS)预处理鞍点矩阵的多尺度算法。在鞍点求解时，加入正则化方法，令方程的收敛效率得到显著提高，同时对HSS方法进行预处理，得到全新的预处理子，且对其参变量采取择优选取，保证算法的可靠性。通过多尺度参变量数值仿真，结果证明本文算法的收敛性极强，具有较高的实用价值。

2 基于正则化选取最优参数

因为方程系数矩阵具备相当程度的复杂度，只使用单纯的迭代算法来求解式(1)，其计算效率较低。而正则化技术则可以充分改进系数矩阵的特质，令方程的求解过程更加便利。

下文将求解式(1)的大规模稀疏线性代数方程组

Ax=b

(1)

式(1)中，A为非奇异矩阵，x，b为列向量。在使用正则化手段的过程中，挑选适当的正则化系数是重要的一步，如果选择的系数太大，即便能够显著改善矩阵条件数，也会使获得的结果与真实结果相差较多，准确度不高；若系数太小又会令条件数无法得到改善，方程收敛速率也很小。因此找到一个合适的正则化系数是加快方程收敛效率的重要保证。

Tikhonov方法是使用最为普遍且高效的正则化方法[6]，其Gauss Markon模型可表示为

(2)

对式(2)采用信道估计算法可得到如下方程

(3)

若式(3)中的条件数较大，也就是在式(3)的方程为病态时，该方程求解结果准确性较低，因此获取的参数估值也相对不可信。按照Tikhonov正则化原则，可把式(2)的正则化估计标准描述为

(4)

式(4)中，K为一个对称的正则化矩阵。由此，可将式(2)方程的求解过程重新表达为

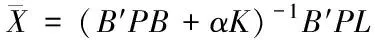
(5)

在K=I的情况下，I为单位阵，可通过式(5)得到

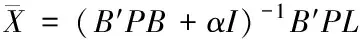
(6)

与式(3)相比较，式(6)左端系数阵增添了α、I，如果α≥0，则称其为正则化参变量。因为增添了这两项系数可以预防方程系数阵产生病态问题，所以可获得参变量的稳定解。可以看出，在均方误差的迹为最小的情况下，Tikhonov正则化方法可以准确得到较为正确的结果，提升了算法的可靠性。由此，可将式(1)方程利用Tikhonov正则化方法转变成求解最小平方解的问题，具体表达为

(7)

式(7)中，L为一个和系数矩阵奇数相等的矩阵，λ为正则化参变量，且此参变量是正数。一般情形下，假设L是单位矩阵I，则式(7)与(8)的求解方程为相等关系

(ATA+λ2I)xλ=ATb

(8)

式(8)中AT是系数矩阵A的转置，xλ是使用正则化处理后的值。在求解式(8)时，如果系数λ的值过大，那么就会导致系数矩阵ATA+λ2I和初始方程的系数矩阵ATA相差较多，最后得到的矢量值与真实矢量值有较大误差；相反，如果系数λ的值过小，正则化算子ATA+λ2I和初始方程ATA过于靠近，就无法具备加速收敛的效果。并且，在式(8)方程的真实操作下，ATA会致使运算数量成倍上升，条件数的数量也会增多，令方程的收敛过程变得更加困难，所以，应该按照原始方程系数矩阵的特征来适时调整正则化方程[7]。

根据ATA算子会引发条件数增多这一规律，在此次研究方法中使用ATA+λ2I算子并不是一个最好的选择。此时，可把式(8)转换成等价模式

(Α+λI)xλ=b

(9)

式(9)将式(8)方程内的λ2利用正实数λ替换。能否选择一个合适的正则化参变量λ是求得精确结果的重要依据。通过上述方程式可知，λ越大，就会越趋近主对角占优，条件数越小，方程组的求解越简单。

在式(9)方程中，A+λI算子和原始系数矩阵的算子的根本区别就是主对角元素，所以λ的选取和系数矩阵有着密切关联。若对额外的矩阵信息为已知状态，如特征值、条件数等，则较容易获取正则化参变量λ。

3 HSS预处理鞍点矩阵的多尺度算法

在明确如何使用正则化方法选取合适的系数后，下面对鞍点矩阵的HSS预处理进行进一步分析，以此将鞍点问题求解的性能实现最优。

HSS是一种对称/反对称分裂的单参数分裂迭代方法，并验证了在α>0时，HSS分裂迭代无条件收敛与线性方程组的唯一解。通常情况下，可将迭代法的模式表示为

x(k)=φk(x(k-1)，…，x(k-l))，k=l，l+1

(10)

式(10)中，φk为迭代算子，x(k-1)，…，x(k-l)为迭代初始值，此种迭代方法为l步迭代算法。在l=1的状态下，则被称之为单步迭代算法；在φk和k互不相关时，也就是φk=φ，则称之为定常迭代法，反之称为非定常迭代法。本文将HSS迭代方法作如下描述：

首先对系数矩阵A进行分裂

A=H+S

(11)

(12)

通常状况下，迭代方法的收敛速率和线性方程的系数矩阵特质有较大关联[8]。在系数矩阵无法满足相关条件时，迭代算法的收敛速率相对缓慢，此时采取预处理可以很好地解决这一问题。通过预处理后的线性方程，其系数矩阵特征被重新完善，可将处理较为困难的线性方程求解问题转变成求出其近似解问题[9]。接下来对HSS迭代方法的预处理子采取进一步研究。

在不更改预处理矩阵结构的基础上，为了提升鞍点问题的求解速度，本文将HSS预处理子的衍生模式表示为

(13)

待求解的线性系统自身是以块结构化所构成的，鉴于该结构的良好性能，提出一新的HSS预处理子(NHSS)

(14)

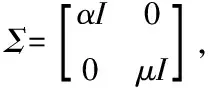
这样，就形成了全新的两步迭代方程组，可将其描述为

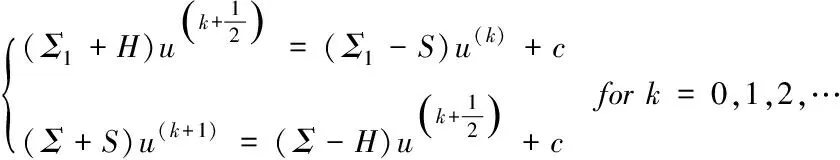
(15)

考虑到有如下预处理子的存在

Mα，β=(Σ+Σ1)-1(Σ1+H)(Σ+S)

(16)

假设μ在Σ中块结构处起到了正则化作用，利用相关运算可得到式(17)，β可以选择任意值

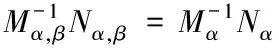
(17)

相应地转变参变量范围也能重新组合成另一种预处理子，将其表达为

(18)

因为其中一个选择参变量和原始矩阵内固定的参变量是相同的，因此能够很直接地看出两种预处理子的差别，两种预处理子内的Σ与Σ1为相等关系。

本文想要构建一种多参数化的预处理子，此种预处理子可以不受到原始矩阵内参变量的影响，防止参变量方位调整所造成的差异化问题。所以要让Σ满足以下条件

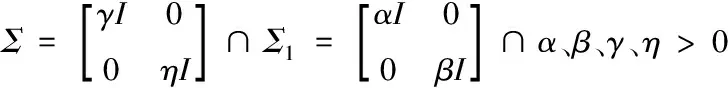
(19)

式(19)中，四个参变量均和原始矩阵A内的参变量无关且各不相同，不是一般性，可构建出如下预处理子

M=(Σ+Σ1)-1(Σ+H)(Σ1+S)

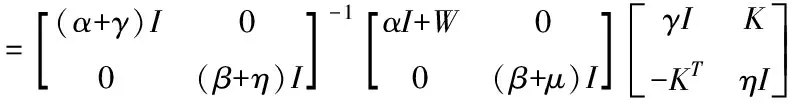
(20)

从式(20)中，可以得到

N=M-A

=(Σ+Σ1)-1(Σ-H)(Σ1-S)

(21)

式(20)中，N为M关于A的剩余矩阵。为了更加具体地分析预处理后的鞍点矩阵的特征值分布状态，需要择优选取预处理子内的参变量，以此保证算法的收敛速率。

将式(20)中的M作为例子，可以看出能够将A分解成

A=M-N

(22)

N=(Σ+Σ1)-1(Σ-H)(Σ1-S)

(23)

同时在式(22)中还隐含M-1A=I-M-1N，由此可以得到

λ(M-1A)=1-λ(M-1N)

(24)

(25)

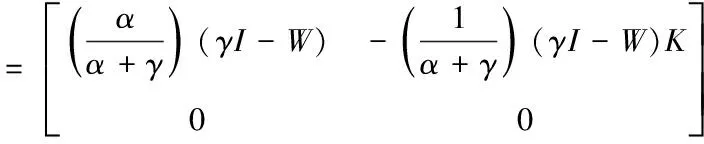
(26)

根据式(26)可以看出β对N的F-范及预处理子M的预处理效果不会产生任何影响。由此可得出以下结论：

正则化参变量μ对运算过程具有十分重要的作用，若Σ—H的块取值是0，则Σ1—S的块对N的F-范不会发生影响，即块内全部的参变量可以选择任意数值；

利用最小化N的迹找出最优参变量，且该参变量可将Σ—H中的块取值为0；

按照式(25)和(26)中A的有效多参数，HSS预处理子可简化为

M=(Σ+Σ1)-1(Σ1+H)(Σ+S)

(27)

通过上述过程，可以加速鞍点矩阵的收敛速度，使线性方程的求解更准确，保证了算法的有效性与适用性。

4 仿真研究

为了验证研究方法的可靠性，进行了仿真。仿真环境采用MATLAB R2012a版软件，文献[10]实验中所使用IFISS软件包生成此次实验所用的线性系统。所用计算机的处理器为Inte1(R) Core(TM)2 Duo CPU T5450@1.66GHZ，Pentium双核2.8 GHz，运行内存为2GB，选用64位Windows 7系统。将研究方法与文献[3]方法(正则化HSS预处理鞍点矩阵的特征值估计)和文献[4]方法(求解鞍点问题的广义正定和反Hermitian分裂方法)进行多尺度参变量数值比较。

若原始矢量均为零矢量，右端矢量是c=He，其中e=ones(m+n，1)，迭代数量为IT，则相对残差可描述为

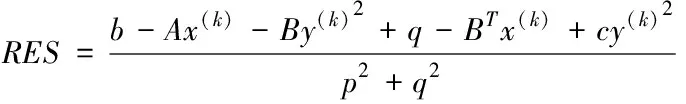
(28)

式(28)中，(x(k)T，y(k)T)T为鞍点矩阵的第k次迭代近似解，在残差符合RES<10-6的条件时，则算法结束。

考虑如下鞍点问题，其系数矩阵依次为

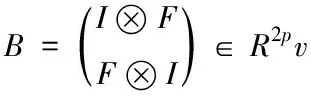
(29)

在此例中，将给定常量v的值设置为0.1和0.01，，针对不同的v，取相应的p=15，20，25，同时α、β∈[0.0001，1]，数值实验结果如表1、表2所示。

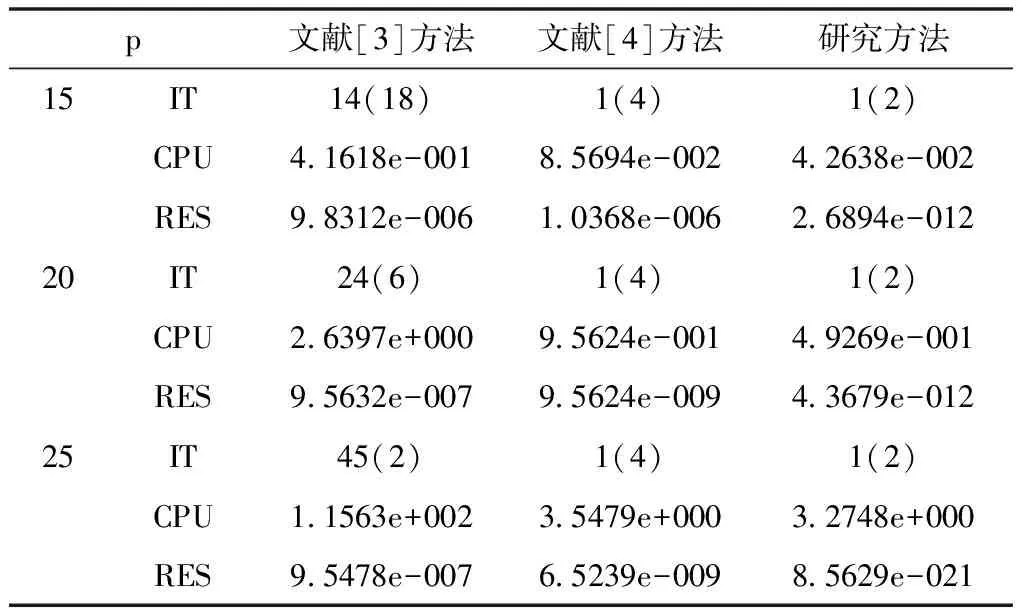
表1 v=0.1的数值实验结果

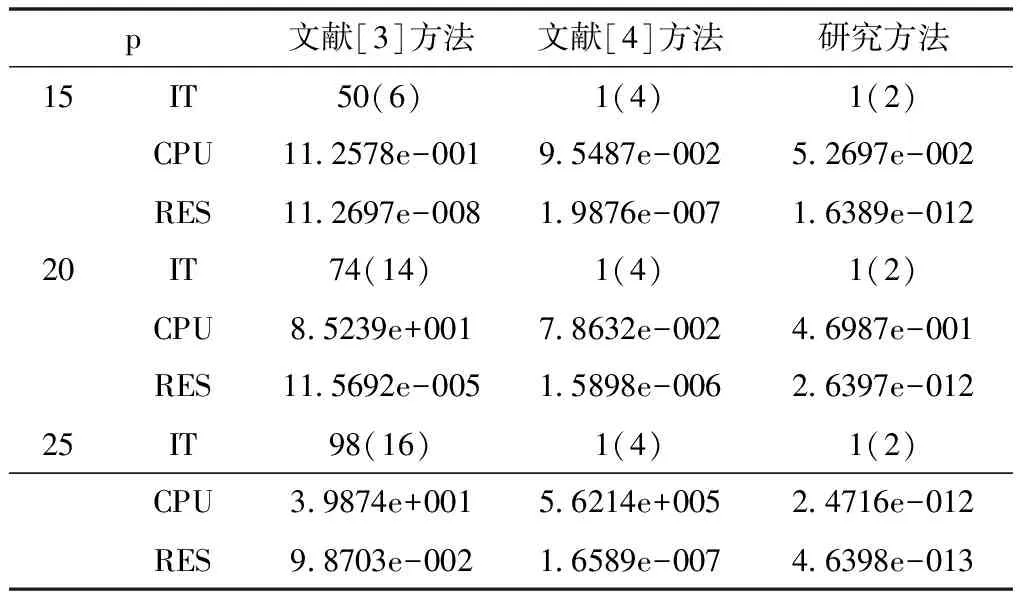
表2 v=0.01的数值实验结果

从表1和表2中可知，在α与β的取值不同时，不管是迭代次数还是CPU，研究方法的数据实验结果均比其它两种方法要好，证明研究方法的可靠性较高，CPU占用率较低。因为对线性方程进行了预处理，重新完善了系数矩阵特征，所以在鞍点矩阵求解有较好的收敛性，使数值结果的准确性较高。

5 结论

为了加强线性方程中鞍点问题求解的收敛性，提高求解的准确性，本文提出一种正则化HSS预处理鞍点矩阵多尺度算法。该方法可以显著提高求解过程的收敛性，且CPU占用率较低，拥有较好的适用性，可为大型线性方程求解提供新的思路。