基于优化导向滤波的模糊图像特征提取仿真

陈 莹，林京君

(1. 吉林建筑科技学院电气信息工程学院，吉林 长春 130114；2. 长春工业大学电气与电子工程学院，吉林 长春 130000)

1 引言

图像作为传递信息的重要载体，对其进行有效的研究与表示，是信息数据处理中的关键之处[1]。图像特征提取作为信息数据处理中的关键技术，常常成为图像信息研究的热点和难点，针对于模糊图像的特征提取，更是大大增加了图像处理的复杂程度，因此，如何准确地提取模糊图像特征成为目前对图像信息研究的重点[2]。

贾旭[3]等人提出基于改进非负矩阵分解的模糊图像特征提取方法，建立非负矩阵分解模型，利用该模型对图像特征进行降维处理；其次把稀疏约束作为该模型的其中一个正则项，便于获取较小数量系数，通过该系数来描述图像特征，对模型的梯度下降进行优化与求解，得到特征基向量与图像特征向量，从而实现模糊图像的特征提取。该方法没有通过导向滤波进行优化，图像边缘保持能力较差，导致图像特征提取运行速度较慢。李钦[4]等人提出基于卷积神经网络的模糊图像特征提取方法，利用卷积神经网络生成图像特征图，对卷积输出层选取对应的特征图，通过特征图建立图像阶层结构，并对此结构进行匹配测试获取到最佳的层级组合，采用信息熵与区域平均的方法分别表示低层级与高层级特征图，最后建立高能力的DHF特征，实现模糊图像的特征提取。该方法没有通过导向滤波进行优化，图像细节信息的滤波效果较弱，导致图像纹理识别率较低。陈超[5]等人提出基于多阈值的模糊图像特征提取方法，采用最大类间方差模糊约束法对模糊图像提取隶属度函数，通过模糊隶属函数对模糊图像中的目标轮廓阈值进行计算，并对阈值进行约束，最终根据曲率符号对模糊图像的轮廓特征提取。该方法没有通过导向滤波进行优化，易丢失图像边缘细节信息，导致图像特征提取结果准确性较低。

为了解决上述方法存在的问题，提出基于优化导向滤波的模糊图像特征提取方法，该方法首先对模糊图像进行去噪处理，其次利用导向滤波对图像进行优化，最终结合图像特征提取方法对模糊图像进行分析与计算以及特征提取[6]。

2 图像预处理

硬阈值及小波阈值去噪方法在对图像处理领域中得到广泛应用，且取得较好的去噪效果，但美中不足的是，对于硬阈值去噪方法来说，对小波系数进行阈值处理时，获取到的估计小波系数值连续性较差，导致对估计小波系数进行小波重构时，取得的信号会处于动荡状态；对于软阈值去噪方法来说，获取到的估计小波系数值虽然连续性较好，但是当小波系数大于阈值时，小波系数与估计出来的小波系数会出现恒定的偏差情况，会影响到重构信号与实际信号间的接近程度，并且重构信号的误差会有所增加[7]。因此，对于以上问题将小波阈值去噪方法进行优化，得到改进的小波阈值去噪方法，其具体步骤如下

下式为新阈值函数，式中，α=0.5。

(1)

式中，Xj，k为小波系数，exp(x)为阈值函数，γ为小波重构值，通过新阈值函数进行小波重构，获取估计信号，即经过去噪后的信号

(2)

3 模糊图像的导向滤波优化

上述获得去噪后的模糊图像，然后对待优化的模糊图像进行假设，定义为R，通过导向滤波进行优化的目的是将获取的输出图像与输入的模糊图像R相似，并且在边缘、纹理等方面要与去噪后的图像Q相同，输出优化后的模糊图像，定义为P。通过导向滤波对图像进行假设，以像素值k为中心的窗口内，其窗口可表示为wk，利用去噪后图像Qi与滤波输出图像Pi间的存在关系建立局部线性模型，即

Pi=akQi+bk，∀i∈wk

(3)

对上式进行求导，得到ΔPi=ak∇Qi。由此可知，去噪后图像Q与输出图像P间存在相同的梯度信息，对去噪后图像的边缘信息可以有效地进行保留，对模糊图像的优化奠定基础，并且促进了模糊图像中的基本形态辨识度。使输出图像P以最大程度保留原始图像R中的模糊信息，需通过最小化代价函数进行计算，即

(4)

对式(6)进行偏导计算，得到下式(5)，式中ε表示正则化参数，wk表示以像素值k为中心的窗口，Qi表示上述去噪后的输出图像，Ri表示初始待优化的模糊图像，从而对最小化代价函数ak和bk进行求解。

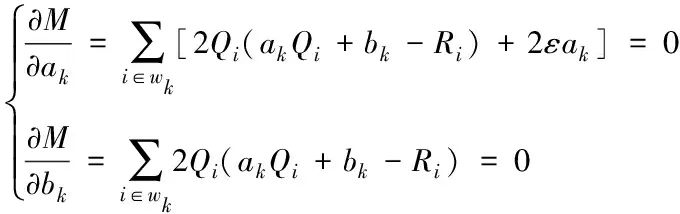
(5)

其中

(6)

4 基于优化导向滤波的模糊图像特征提取方法

在上述对模糊图像进行去噪处理以及对去噪后的图像通过导向滤波进行优化的基础上，对模糊图像进行特征提取，首先建立模糊BP神经网络模型，如图1所示，在组建网络时，首先对输入数据的类型进行分析，由于输入数据是图像类型，图像信息不易量化，并且大部分为模糊型数据，因此需引入模糊集，对数据进行处理，主要是通过隶属函数对图像数据进行分析与计算，隶属函数可将图像信息进行划分，分为高、中、低三个层次，并以此作为输入层的三个节点，通过神经网络的输入层将图像信息进行输入，并进行相应训练与提取[9]。

图1 模糊BP神经网络模型

由于对模糊图像信息进行计算时，引入的是模糊集合，模糊集合作为输入层的输入数据，需对每个输入点赋予相应的加权算子，且取值区间在[0，1]内，模糊加权算子分别由模糊特征隶属度与特征矩阵构成，并定义为E，其模糊加权算子的构成具体定义为E={e1，e2，e3}。

其中

(7)

式中，模糊图像归一化的模糊特征隶属度表示为E，所对应的特征矩阵表示为A，对模糊图像特征隶属度进行计算，对于图像所对应的特征矩阵通过特征判别式进行判断，当矩阵满足条件时，证明该矩阵中具有该特性，依次进行判断与记录，直到整个图像进行完，最终对特征的记录值表示为Earc，Erect，Ethread。

隐含层的主要作用是将上述三个节点所对应的三种结果，进行结合，因为在最终输出层，只需要一种结果来体现，为了解决该问题，利用点与点之间的相关性概念进行结合[10]。

对最终获取的向量设置为K，其到达隐含层相对三个节点的对应向量则表示为K1，K2，K3，相应均方差计算公式为

E2=(K-K1)2+(K-K2)2+(K-K3)2

(8)

采用最小二乘法对K值进行确定w1，w2，w3

(i=1，2，3)

(9)

通过上式计算取得w1，w2，w3，均会具有归一性，把三个结果进行归一化处理，得到一个输出结果，即输出对特征矩阵的提取结果[11]。

5 实验与结果

为了验证基于优化导向滤波的模糊图像特征提取方法的有效性，需对基于优化导向滤波的模糊图像特征提取方法进行相关实验，实验在Eclipse软件中ARM(armeabi-v7a)CPU，343M，Android4.4系统的计算机上进行相关测试。实验中选取的移动设备配置：SamsungI9100，CPU型号为Exynos4210，双核处理器，内存为2GB。实验数据是在互联网中获取以及实际移动设备拍摄的图片，形成模糊图像集，并将模糊图像集按照图像大小类型进行划分，分为a1～a1010种模糊图像集类型，分别作为本次实验的模糊图像测试数据，由于不同图片含有不同的旋转角度、亮度以及含有不同噪声等变换形成的图像集，进行相关实验，使实验结果更具有说服力，以及方法可行性更强。

分别采用文献[3]方法、文献[4]方法、所提方法进行相关实验，将3种不同方法对模糊图像集a1～a10进行特征提取运行时间(s)对比，对比结果如表1所示。

表1 不同方法对图像特征提取运行时间对比(s)

由表1数据可知，所提方法对模糊图像特征提取的时间最小，证明所提方法的提取特征性能更好，因为所提方法在对模糊图像特征进行提取时，利用导向滤波对图像进行优化，通过窗口内的求和运算快速实现图像优化，且图像边缘保持能力较高，进而缩短了对图像特征提取的运行时间。

将图像纹理特征值作为测试指标，对比不同方法的图像纹理识别率，具体测试结果如表2所示。

表2 不同方法对图像纹理识别率对比(%)

分析表2数据可知，文献方法的图像纹理识别率均低于所提方法，证明所提方法提取图像特征更加准确，图像纹理识别率更高，所提方法在对模糊图像特征进行提取时，通过导向滤波对图像进行优化，使图像细节信息呈现较为平滑状态，并获得较好的滤波效果，促使图像特征提取的纹理识别率更高。

为了验证不同方法对模糊图像特征的提取效果，将3种方法对模糊图像特征提取进行相关测试，测试结果如图2所示。

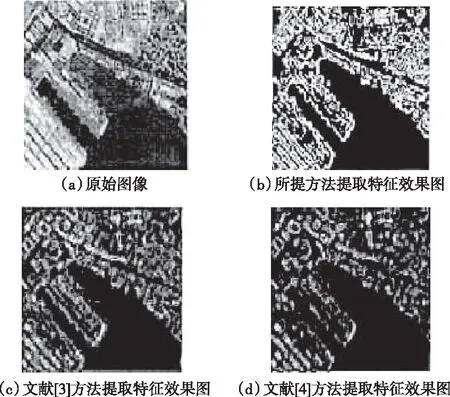
图2 不同方法对模糊图像特征提取效果对比

据图2数据可知，所提方法的特征提取效果好于方法2和方法3，特征提取准确性更高，所提方法在对模糊图像特征进行提取时，利用导向滤波对图像进行优化，有效避免了图像边缘细节信息丢失以及图像细节信息被损坏，使边缘保持能力恰好满足于模糊图像优化时的需求，从而提高了对模糊图像特征提取的准确性与高效性。

6 结束语

提出基于优化导向滤波的模糊图像特征提取方法，首先对模糊图像进行去噪处理，其次利用导向滤波对模糊图像进行优化，通过窗口内的求和运算快速实现图像优化，最终在导向滤波优化的基础上对模糊图像进行特征提取，构建模糊BP神经网络模型，采用隶属函数对图像数据进行计算与提取。该方法有效解决了目前方法中存在的问题，在提高图像特征提取运行速度的同时，增加了对图像特征提取的准确性。