基于混合模拟退火算法的机场进场程序优化
陈 昇,周 隽,2*,胡小兵,马 霁,2
(1.中国民航大学中欧航空工程师学院,天津 300300;2.中国民航大学中法联合空管应用数学研究中心,天津 300300;3.中国民航大学电子信息与自动化学院,天津 300300)
0 引言
机场终端区作为空中交通运输的起点和终点,是最为复杂的空域类型之一,同时也是保证航班高效有序运行的关键环节。目前,由于终端区空域容量饱和,国内外许多大型机场都面临航班延误的问题,只有突破机场终端区空域的容量瓶颈,才能保障民航运输的稳健发展。传统的终端区扩容方式以新建机场和跑道为主,需要投入大量的人力物力且工期较长。此外,也可以通过合理设计机场进离场程序来从战略层面提升空域资源利用率,进而达到提升终端区容量的目的。相比之下,后者具有成本较低、易实施的优势。区域导航RNAV(Rules for implementation of area NAVigation)是一种新兴的导航规范[1],与传统导航方式相比具有导航精度高、航路规划较灵活等优势,尤其适用于机场终端区空域的程序设计。
当前绝大部分机场进离场程序是根据机场地理位置和周边环境,以国际民航组织文件DOC8168-POS/611 为标准,通过人工设计并借助计算机辅助软件绘制完成的[2-3],设计过程比较耗时,且方案的有效性大多取决于人员经验,缺乏对于路径长度等指标的定量分析。特别是对于吞吐量较大的机场,进场程序通过逐步汇聚的方式将交通流由终端区边界的多个进场点逐步引导至最终进近点(Final Approach Fix,FAF)。进场程序的汇聚构型与航路汇聚顺序、组合方式及汇聚点位置紧密相关。鉴于其拓扑结构的复杂性,单纯基于经验进行人工设计很难充分发挥终端区的空域资源优势,因此,借助优化算法进行自动化的程序设计可以为程序设计人员提供必要的决策支持,提高设计效率,并且有利于从战略层面优化终端区空域资源配置。
进场程序的优化属于路径规划问题的范畴[4-5]。按照空间维度可以将相关研究划分为二维和三维,按照路径数量又可以划分为单一路径和多条路径。二维层面的研究成果比较丰富[6-9],研究关键点在于对障碍物的建模方式以及规避障碍物的路径搜索算法。例如,文献[6]将障碍物建模成二维凸包,通过顺时针或逆时针转弯的方式规避障碍物,并应用遗传算法搜索最短航路。二维层面的路径规划不符合终端区内航空器的实际运行特点,因此需要对模型和算法进行三维的拓展[10-12]。文献[11]对航路及障碍物进行了三维建模,提出了顺时针转弯、逆时针转弯、保持飞行高度三种障碍物规避方式,并应用了分支定界法对一条进离场程序进行优化。文献[12]应用改进的遗传算法对一条三维的无人机路径进行规划,并采用三次B 样条曲线对规划出的路径进行平滑,算法具有较好的环境适应性。三维空间的多条路径规划问题复杂度较高,相关研究还比较有限[13-14]。文献[13]提出了基于A*算法的多条进离场程序优化,考虑了包括最大最小爬升及下降角度、平滑转弯等航空器的运行约束。文献[14]在文献[11]的基础上增加了多条程序间最小安全间隔的约束,并应用改进的分支定界法设计多条进离场程序。
进场程序汇聚结构的优化对于大型机场有重要意义。当前国内对于航路汇聚的研究侧重于点汇聚进近程序的设计和风险评估[15-16],以及交汇航路的交通流特征研究[17],国外的相关研究也比较有限[18-20]。文献[18]通过改变航路汇聚方式及汇聚点位置构造不同的汇聚结构,并测试其对空域容量的影响。文献[19]将二维空域进行网格化划分,在考虑规避障碍物、最大航向角改变量等约束下,建立整数规划模型进而生成具有汇聚结构的多条二维进场程序。文献[20]对进离场程序进行三维建模,每条程序由一条水平面的折线和竖直平面的扇形区域构成,考虑了障碍物规避和航路间安全间隔的约束,应用模拟退火算法优化进离场程序的汇聚和发散结构。
虽然针对航空器的路径规划问题已经进行了诸多研究,但仍然存在以下两点不足:
1)进场程序的模型没有充分考虑同一航路上各航空器下降角度不同的特点;
2)多条进场程序的优化,尤其是针对其三维汇聚结构的优化研究仍有待拓展。
本文针对上述问题,首先结合RNAV 的导航规范及航空器在竖直平面内下降角度的特点,建立单一的进场程序三维模型;在此基础上以最小化进场程序总长度为目标,以障碍物规避、进离场程序间安全间隔、航向角改变量为主要限制条件,建立完整的数学模型。其次,开发了一种基于模拟退火算法与改进A*算法的混合启发式算法,其中模拟退火算法用于控制解空间的搜索过程,即确定与进场程序汇聚构型相关的决策变量取值;改进A*算法用于搜索邻域最优解,即求解与决策变量相应的总长度最短的汇聚构型。最终仿真实验验证了本文模型和算法的有效性。
1 进场程序汇聚结构模型
首先建立单一的进场程序三维模型,在此基础上提出关于多条进场程序汇聚结构的决策变量;其次给出所需考虑的约束条件及相应的数学表达式;最后明确优化问题的目标函数。
1.1 单一进场程序三维模型
单一进场程序的三维模型由水平平面分量与竖直平面分量组成。在水平平面,程序的投影为一条连接一系列散点的折线,起点为一个进场航路点,终点为FAF,中间散点为航路汇聚点或导航点。连接两个相邻散点的直线段在实际运行中对应一个点对点的直飞航路段,满足RNAV 的导航规范。在竖直平面,由于航空器的性能差异和外界环境的影响(风向、风速等),同一航路上的不同航空器有不同的下降角度。因此将进场程序在竖直平面建模成由最大下降角αmax,LD和最小下降角αmin,LD所包围的类似扇形区域,如图1(a)中的阴影部分所示。程序水平分量上的任意一点p对应竖直分量上的一个高度区间[hp,inf,hp,sup](如式(1)、(2)所示):

其中:hFAF表示FAF 点的高度;d(p,FAF)表示点p到FAF 的水平面飞行距离。图1(b)为一条进场程序的三维示意图,其水平分量是依次连接p1、p2、p3和FAF 的一条折线,折线上任意点在竖直平面对应的高度区间构成了程序在竖直平面的分量,如图中阴影区域所示。

图1 进场程序建模示意图Fig.1 Schematic diagrams of arrival procedure modeling
多条进场程序通过彼此汇聚最终收敛到FAF。图2 所示的汇聚结构包含五条进场程序。以加粗线段所表示的进场程序为例,其水平面分量是由8 个散点{pi∪FAF|i=1,2,…,7}依序相连所组成的折线,其中p1为进场点,p3、p5、p7为汇聚点,其余为普通导航点。为便于后文表述,给出“航路段”的定义:航路水平分量上的以相邻进场点、汇聚点或FAF 点为端点的部分折线段。令点p、q表示一个航路段的两个端点,则将该航路段记作。
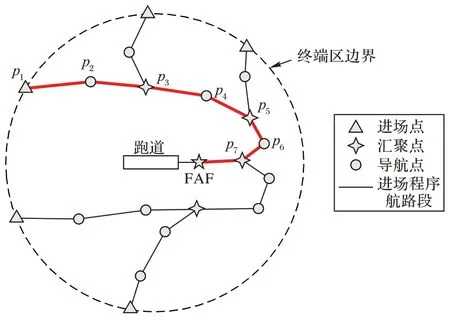
图2 进场程序汇聚结构示意图Fig.2 Schematic diagram of merging structure of arrival procedures
1.2 汇聚结构决策变量
多条进场程序汇聚结构的布局主要与两方面因素相关:一方面是进场程序汇聚方式的决策,即参与汇聚的程序的组合方式和汇聚的先后顺序;另一方面是由汇聚所形成的汇聚点的具体位置。为避免多条进场程序同时汇聚于一处而造成过大的管制负荷,人为地规定每次汇聚只有两条程序参与。为了便于表示汇聚结构,以下首先介绍对进场点与汇聚点的排序标号方法,随后提出模型的决策变量。
1.2.1 进场点与汇聚点编号
令Ne∈N+表示进场点个数,则进场点的编号由1 递增至Ne,将进场点及其相应水平面坐标的集合记作{ei(xei,yei),i=1,2,…,Ne},具体的排序方式为:构造以跑道中心点P(xP,yP)为起点、以FAF 点为终点的基准向量PF,同时构造以P(xP,yP)为起点、以各进场点为终点的向量集合V={Pei|i=1,2,…,Ne}。选取V中与PF沿顺时针方向夹角最小的进场点,并将其标记为1 号点,其他进场点按顺时针方向夹角递增的顺序进行标号。图2 的汇聚结构中共有5 个进场点,其编号如图3 所示。
令Nm∈N+表示汇聚点个数,则汇聚点的编号由Ne+1递增至Ne+Nm,将汇聚点及其相应水平面坐标的集合记作{mj(xmj,ymj)|j=1,2,…,Nm}。由于人为地规定每次汇聚只有两条程序参与,通过简单计算可知,汇聚点数量比进场点数量少一个,即Nm=Ne-1。在对汇聚点进行排序编号前,需要确定汇聚点所在“层数”:将进场点定义为第1 层汇聚点,将由两个以进场点为起点的航路段汇聚所形成的汇聚点定义为第2 层汇聚点,当k≥3 时,将由以第k-1 层和第l层(l≤k-1)的两个汇聚点为起点的航路段汇聚所形成的汇聚点定义为第k层汇聚点。汇聚点的排序首先取决于该汇聚点所在的汇聚层数,层数越小的排序越靠前;对于同层汇聚点,需要比较该汇聚点所在航路段的起始端点的标号,起始端点标号较小的汇聚点的排序靠前。图2 的汇聚结构中共有4 个汇聚点,其标号如图3 所示。为简化表述,将生成第k层汇聚点所对应的汇聚过程称为“第k层汇聚”。
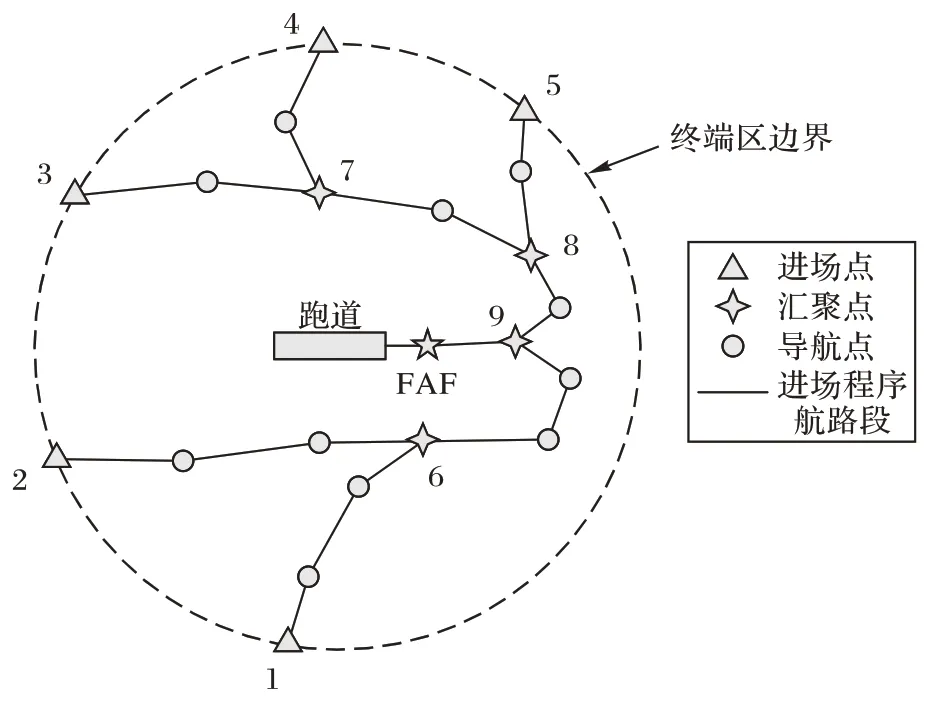
图3 进场点、汇聚点编号示意图Fig.3 Schematic diagram of arrival points and merging points numbering
1.2.2 汇聚方式的决策
引入大小为Nr×Ne的矩阵M1以表征进场程序的汇聚过程,其中Nr为汇聚结构的层数(按1.2.1 节定义),Ne为进场点个数。矩阵M1中元素取值的集合为{0,1,…,Ne+Nm},除0 外每个数值代表一个进场点或汇聚点的编号(按1.2.1节定义)。
同时引入含有Nr-1 个行向量的集合M2={V1,V2,…,}以表示参与汇聚航路段组合方式的决策。行向量Vi表示矩阵M1第i行中元素值所对应的进场点或汇聚点在第i+1 层汇聚中的组合方式。每个行向量中元素的取值为0 或1,分别表示以相应的进场点或汇聚点为起点的航路段不参与或参与下一层汇聚。
确定矩阵M1和集合M2中元素取值的过程实际上即是确定汇聚方式决策的过程,具体步骤如下:
1)根据进场点编号生成矩阵M1中的第一行元素,即[1,2,…,Ne];
2)根据矩阵M1第i行中元素的取值,选择集合M2中行向量Vi的取值;
3)根据集合M2中的行向量Vi的取值,确定矩阵M1中第i+1 行中元素的取值;
4)重复第2)~3)步直至所有进场程序全部汇聚,此时矩阵M1和集合M2中所有元素的取值确定。
其中第2)步是生成不同汇聚组合方式的关键步骤,具体来说:将矩阵M1的第i行中连续两个及以上取值相同的元素归为一组。在对Vi的第j个元素进行赋值时,假设该元素前面的j-1 个元素中有k1个“1”和k2个“0”,则当第j个元素取“0”时,表示以矩阵M1第i行中的第2k1+k2+1 个元素组对应的进场点或汇聚点为起点的航路段不参与下一层汇聚;取“1”则表示以矩阵M1第i行中的第2k1+k2+1 和2k1+k2+2 个元素组对应的进场点或汇聚点为起点的航路段在下一层汇聚。第3)步的具体实现过程为:令aij表示矩阵M1中第i行第j列元素的值,当以max({akj|k=1,2,…,i-1})为起点的航路段不参与第i层汇聚时,取aij=0;当以max({akj|k=1,2,…,i-1})为起点的航路段参与第i层汇聚时,取aij∈{Ne+1,Ne+2,…,Ne+Nm},具体取值按1.2.1 节定义。以图3 中的汇聚结构为例,相应的汇聚方式决策对应的矩阵,集合。
1.2.3 汇聚点位置的决策
进场程序通过汇聚结构逐渐向FAF 点收敛。根据这一特点,基于汇聚的层数及参与汇聚两航路段起始点的位置,人为地设定每个汇聚点位置的选择范围,其原则是令位于较高汇聚层的点比位于较低汇聚层的点更靠近跑道。设以点A(xA,yA)、点B(xB,yB)为起点的航路段汇聚到点C(xC,yC),且点C位于第k层汇聚,则点C水平面坐标(xC,yC)的选择范围为扇环ϒC,如图4 所示。其中表示连接点p和点q的直线段。具体计算方法如下:

图4 汇聚点位置的取值范围示意图Fig.4 Schematic diagram of value range for locations of merging points
1)计算所有进场点到FAF 的最短直线距离,记作R1=,其中表示连接FAF 点与进场点ei的直线段的长度。
2)令K1表示矩阵M1的行数,构造以FAF 为圆心的K1个同心圆,其中第j个同心圆Πj的半径为Rj=。
3)以FAF 为圆心、RC为半径作圆ΠC,其中RC=分别表示连接FAF 与点A、点B的线段的长度。
1.3 约束条件
机场终端区进场程序规划需要考虑的主要限制条件包括:障碍物的规避、进离场程序间的安全间隔以及航向角的最大改变量。
1.3.1 障碍物的规避
机场终端区的障碍物包括禁飞区、山区、城市等。对于一个障碍物(包括其保护区),令Γobst表示包裹该障碍物水平面投影的最紧凸集,令hobst,inf和hobst,sup分别表示该障碍物在竖直平面高度的下确界与上确界,则该障碍物的三维模型记作Ωobst={(x,y,z)|(x,y)∈Γobst,z∈[hobst,inf,hobst,sup]}。令表示连接导航点p、q的直线段,判断与Ωobst是否存在冲突的方法为:当时,二者不存在冲突;否则需要进一步在竖直平面检测,若式(3)或(4)成立,则与Ωobst不存在冲突。


1.3.2 进离场程序间的安全间隔
为从战略层面减少进离场航班流之间的潜在冲突,进离场程序间需要满足最小安全距离,其中最小水平和竖直安全距离分别记作δH、δV。令p、q表示某进场程序上的两个相邻散点,令p′、q′表示某离场程序上的两个相邻散点,则当线段的最小距离大于δH时,二者不存在冲突;否则需要进一步验证二者在竖直平面的相对位置关系,当式(5)或(6)成立时可以判定二者不存在冲突。
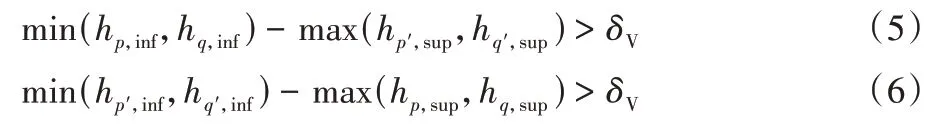
1.3.3 航向角的最大改变量
过大地改变航向角量会使航空器发生大幅度滚转,不利于正常飞行。因此,进场程序水平分量上的任意两个相邻直线段对应的向量夹角应满足式(7):

其中:θmax为最大航向角改变量。
1.4 目标函数
考虑到汇聚后的航路段实际上由多个进场程序共同使用,因此本文的优化目标为各个航路段长度的加权和,即加权航路长,如式(8)所示:

其中:Nt表示航路段总数量;Li(i∈[1,Nt])表示第i个航路段的长度;αi表示经过第i个航路段的进场程序个数。以图3中的汇聚结构为例,连接汇聚点6 和9 的航路段是由连接进场点1 和汇聚点6 的航路段及连接进场点2 和汇聚点6 的航路段汇聚而成的,因此该航路段对应的权值为2。
综上所述,本问题的输入参数为:
1)机场跑道中心点坐标P(xP,yP);
2)FAF 点坐标及高度hFAF;
3)进场点坐标集合{ei(xei,yei),i=1,2,…,Ne};
4)进场程序最大、最小下降角度:αmax,LD、αmin,LD;
5)离场程序构型;
6)机场终端区内障碍物信息;
7)进离场程序间最小水平、竖直间隔:δH、δV;
8)最大航向角改变量θmax。
进场程序汇聚结构模型可表示为:


对本问题的求解可分解为两个关键子问题:第一个子问题是求解合理的汇聚方式决策和汇聚点位置决策,这是一个典型的组合优化问题。其中,汇聚点位置决策的组合数量随进场程序数量呈指数增长。第二个子问题是在已知汇聚方式和汇聚点决策后,求解满足约束条件的最优路径,这是一个典型的路径规划问题,其求解难度在于如何在三维空间处理路径规划的多个约束条件。
2 算法实现
根据对数学模型的分析,规划进场程序的汇聚结构首先需要搜索合理的决策变量组合,其次要针对给定的决策变量构造满足约束条件的最短航路。对于决策变量的求解,确定性算法(例如分支定界法)能够收敛到全局最优解,但在类似问题的应用中,其计算效率较低。例如,文献[19]建立了进场程序汇聚结构的二维整数规划模型,并应用分支定界法求解。当进场程序数量为4 时,根据不同的目标函数,其最短和最长计算耗时分别为993 s 和9 447 s。随着数学模型扩展到三维空间、进场程序数量和汇聚点备选位置数量的进一步增加,分支定界法的计算耗时将显著增长。与确定性算法相比,启发式算法具有一定随机性,但是能够在合理的计算时间内提供比较优质的解。因此,为了在提升计算效率的同时得到比较满意的解,本文提出了基于模拟退火算法与改进A*算法的混合优化方法。其中,模拟退火算法用于控制对决策变量组合解空间的搜索;对于每一个模拟退火算法的邻域解,改进A*算法用于逐段计算满足限制条件的最优航路段,进而获得与决策变量相对应的进场程序汇聚结构。
2.1 模拟退火算法
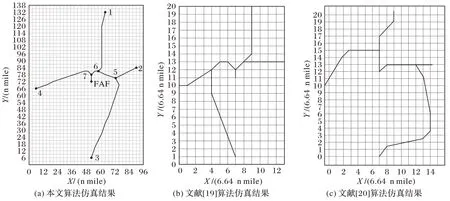
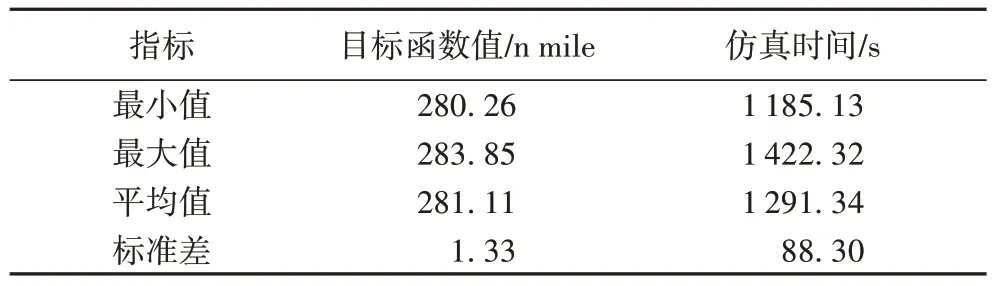
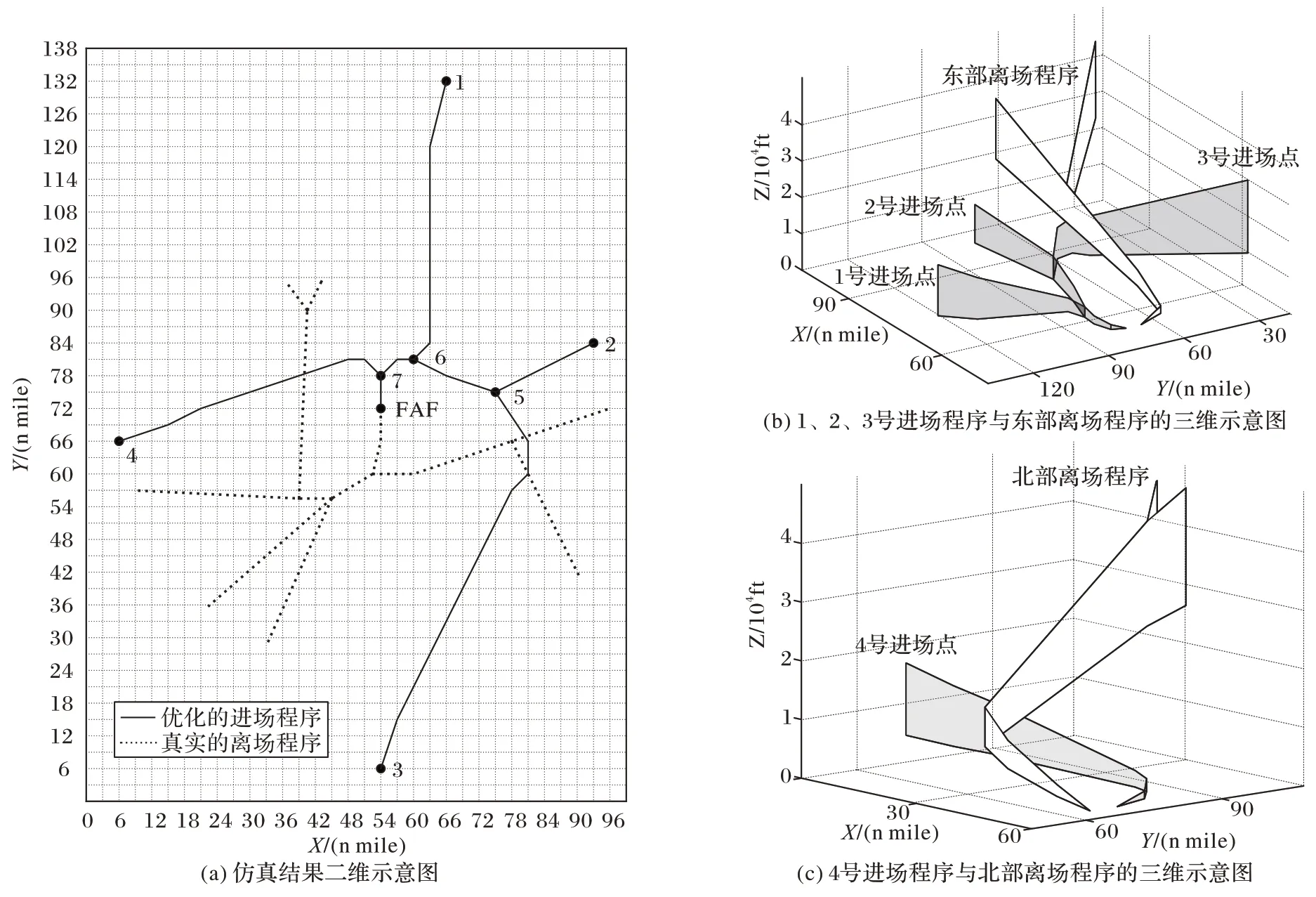
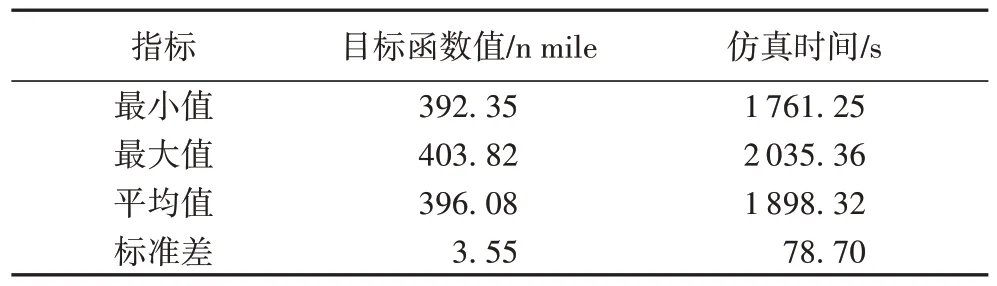
模拟退火算法借鉴了对固体物质进行退火处理的过程。以控制参数T模拟固体温度,每一个温度阶梯需进行K次迭代,将初始温度、终止温度和温度衰减系数分别记作T0、Tf、β。在求解过程中,每个解X相应的成本函数记作F(X)。每次迭代基于当前解Xcur生成新的邻域解Xnew,并比较F(Xcur)与F(Xnew)。若F(Xnew) 本文提出的模拟退火算法中的每一个当前解Xcur包含着一组汇聚方式决策和汇聚点位置决策的组合。在生成Xcur的过程中:第一步应生成汇聚方式的决策,并在此基础上确定汇聚结构中汇聚点的数量及每一条进场程序由进场点起按序所经过的每一个汇聚点(见1.2.2 节);第二步再生成相应的汇聚点位置决策,即确定每一个汇聚点的坐标(见1.2.3 节)。随后,应用改进A*算法(见2.2 节)逐段计算每条进场程序上连接相邻进场点、汇聚点、FAF 的航路段最优构型,并根据式(8)计算相应的加权航路长,记作F(Xcur)。 基于当前解Xcur生成邻域解Xnew是模拟退火算法的核心内容,也是算法遍历决策变量组合解空间的关键。解Xcur的品质主要取决于两方面:一方面是航路汇聚方式是否合理;另一方面是汇聚决策不变时,汇聚点位置选择是否仍能改进。因此,在本文提出的模拟退火算法中,为了避免上述不合理的决策变量组合,构造了“汇聚方式修正算子”和“汇聚点位置修正算子”,分别用来检测相应决策变量的合理性并予以必要的修正。每次迭代以概率P0执行汇聚方式修正算子,以概率(1-P0)执行汇聚点位置修正算子,进而基于当前解Xcur生成邻域解Xnew。两个算子的具体运算过程如下。 2.1.1 汇聚方式修正算子 不合理的汇聚方式会导致不同进场程序的航路段间发生交叉,如图5(a)中虚线圆圈标识的区域所示;或导致某段航路为规避冲突而大幅度绕弯,如图5(b)中连接2 号进场点和6 号汇聚点的航路段所示。上述情况均不利于飞行员操作及空管员管理,应尽量避免。因此,对于每个当前解Xcur,首先执行航路交叉的检测和标记:对于当前解Xcur的进场航路段进行逐对逐段检测,若发生航路段交叉,则将这两条航路段的两个端点分别标记1 次。若不存在航路交叉,则执行航路段弧弦比的检测和标记,其中弧弦比是指某航路段的实际长度与连接其两个端点的直线段的长度的比值。逐段计算当前解Xcur中每条进场程序上各航路段的弧弦比,当比值大于阈值ε1时,对相关的航路段的两个端点标记1 次。检测完成后,选取被标记次数最多的进场点或汇聚点,在Xnew的决策向量集合M2,new中修改与该点相关的决策方式。若两种情况均不存在,则随机选择Xcur的决策向量集合M2,cur中的一个向量,从该向量起进行微调,生成新的M2,new。最后,根据M2,new中元素取值的改变重新生成相应的汇聚点位置决策。 图5 不合理的汇聚方式的示意图Fig.5 Schematic diagram of unreasonable merging modes 2.1.2 汇聚点位置修正算子 当汇聚点位置不合理时,相关航路段会出现为满足最大航向角改变量的约束而绕弯的情况。对于当前解Xcur中的每条进场程序,逐段计算各航路段上的航向角改变量的绝对值之和。若大于阈值ε2则对该航路段的两个端点标记1 次。检测完成后,选择被标记次数最多的汇聚点,并在1.2.3 节中定义的相应扇环内随机选取新的位置坐标。若未检测出上述情况,则随机选取一个汇聚点并改变其位置坐标。 在每次模拟退火算法生成一个新的邻域解后,相应汇聚结构中每条进场程序由进场点起到FAF 点为止按序所经过的每一个汇聚点也随之确定。则对于每条进场程序上的每一个航路段,其两个端点坐标已知,因此可以应用A*算法构造连接两个端点且满足约束条件的最优航路段。A*算法是解决最短路径问题最常用的算法之一,一般应用于网格图或加权图中。为了对搜索空间进行离散化,采用二维网格覆盖终端区在水平平面的投影,其中每一个单元格边长记作δ。进场点、汇聚点、FAF 点及定义障碍物边界的散点均取在二维网格的节点处。结合本问题模型的特点与求解难点,与传统的A*算法相比,本文算法做了如下三方面改进: 1)传统的A*算法在每次迭代中只扩展与当前最优节点直接相邻的8 个节点,这种方法可能会导致最优路径的航向改变过于频繁,路径不够平滑且总长度较长。因此,在改进A*算法中将展点数量扩大为48 个。设当前点p的坐标为(xp,yp),改进后的备选展点集合为,为避免在同一方向重复展点,将展点方向重复的外层点剔除。 2)传统的A*算法主要在二维平面进行路径规划,改进A*算法拓展到三维空间,每个节点对应一个高度区间。以备选节点qi为例,它所对应的高度区间为,根据式(10)~(11)计算: 其中:(hp,inf,hp,sup)表示当前节点的高度区间;(αmin,LD,αmax,LD)表示进场程序的最小、最大下降角。 3)传统的A*算法通常只考虑障碍物规避这一单一约束,改进A*算法考虑1.3 节中所有约束条件。首先是航向角改变量约束,令节点u(xu,yu)表示节点p的父节点,则向量up和pqi应满足式(7);其次是根据1.3.1 节的方法判断线段是否满足障碍物规避的约束;最后,对已知的离场程序构型进行离散化,再将离场程序上离散后的线段按照1.3.2 节的方法逐个与进行冲突检测,以判断是否满足航路间隔约束。只有满足所有约束才能对该节点进行展点。 为测试算法的有效性和运算效率,并与现有相关研究的仿真结果[19-20]进行对比,选取瑞典阿兰达(Arlanda)机场和上海浦东机场的终端区空域布局进行仿真实验,将机场跑道位置、进场点数量及坐标、离场程序构型作为已知参数。离场程序的模型与1.1 节中定义的进场程序模型相似。测试中,根据实际进离场航班航迹剖面图选取进场程序最小、最大下降角分别为1°和3°,离场程序最小、最大爬升角分别为4.5°和7.5°。与模拟退火算法相关的参数如表1 所示,其他用户设置的参数如表2 所示。在图6~8 中,实线表示优化的进场程序,虚线和点划线分别表示该机场实际的离场程序和进场程序,与进场点、汇聚点相邻的数字表示其编号(按1.2.1 节定义)。所有仿真测试均在3.0 GHz 处理器,16 GB 运行内存的Windows 10 平台运行。 表1 模拟退火算法的相关参数Tab.1 Related parameters of simulated annealing algorithm 表2 其他用户设置参数Tab.2 Other user-defined parameters 在笛卡儿坐标系中,以经纬度(58.87°N,16.73°E)为坐标原点,跑道中心点P和FAF 所对应的坐标点分别为(54,66)和(54,72)、(54,72),FAF 高度为0。在图6(a)和图7(a)中,网格的单元格边长为δ=3 n mile。 1)算例1:4 个进场点且不考虑离场程序的仿真实验。 首先对4 个进场点且不考虑离场程序的情况进行10 次仿真实验,仿真结果的统计数据见表3。其中第2 次实验最终解的目标函数值最小且计算耗时最短,加权航路长度为277.02 n mile,计算耗时为127 s,相应的进场程序汇聚构型如图6(a)所示。在相同进场点布局且不考虑离场程序的情况下,文献[19]中的最优解如图6(b)所示,其中网格单元的边长为6.64 n mile,相应汇聚结构的加权航路长度为286 n mile,计算耗时为993 s。经对比,本文提出的混合模拟退火算法在航路长度上缩短了约3%,计算耗时减少了约87%。虽然文献[19]应用了确定性算法求解,但其网格单元边长是本文算法中的2.2 倍。因此,在相同终端区范围内,本文算法的网格节点数量较多,为汇聚点位置的决策和A*算法的展点提文供了更多可能性,最终求得的路径更加平滑且长度更短。文献[20]也针对相同算例进行测试,最优解如图6(c)所示,相应汇聚结构的加权航路长度为339 n mile,计算耗时约为3 s,虽然运算效率较高但航路长度较本文结果增加了22%。通过对比可见,本文提出的混合模拟退火算法所规划的路径长度最短,计算耗时比较合理,更适合以最小化路径长度为目标的战略层面的进场程序设计。 表3 算例1的10次仿真结果统计Tab.3 Result statistics of 10 simulations of example 1 图6 算例1仿真结果的示意图Fig.6 Schematic diagrams of simulation results of example 1 2)算例2:4 个进场点且考虑离场程序的仿真实验。 将阿兰达机场实际离场程序作为已知参数,构造进场程序汇聚结构,此时需要考虑进离场程序间的最小安全距离的约束。进行10 次仿真实验,仿真结果的统计数据见表4。其中,最短的加权航路长度为280.26 n mile,相应的进场程序汇聚构型如图7(a)所示。通过与图6(a)的进场程序结构对比发现,由于考虑航路安全间隔约束,连接3 号进场点和5 号汇聚点的航路段为规避终端区东部的离场程序而发生转弯绕飞,使得3 号进场程序长度增加。此时3 号进场程序与东部的离场程序不存在三维冲突,如图7(b)所示。类似地,4 号进场程序与终端区北部的离场程序在水平面相交,但二者在竖直平面满足最小安全间隔,如图7(c)所示。与算例1仿真结果对比,在考虑离场程序时,由于问题复杂度增加,算法运行时间明显增加。 表4 算例2的10次仿真结果统计Tab.4 Result statistics of 10 simulations of example 2 图7 算例2仿真结果的示意图Fig.7 Schematic diagrams of simulation results of example 2 在笛卡儿坐标系中,以经纬度(29.87°N,120.27°E)为坐标原点,跑道中心点P和FAF 所对应的坐标点分别为(80,81.2)和(84,72)。在图8(a)中,网格的单元格边长为δ=3n mile。 将浦东机场实际离场程序作为已知参数,构造进场程序汇聚结构。进行10 次仿真实验,仿真结果的统计数据见表5。其中第4 次实验最终解的目标函数值最小,为392.35 n mile,相应的进场程序汇聚构型如图8(a)所示。以7 号汇聚点和9 号进场点对应的航路段的三维结构为例,它们与终端区东南部的离场程序不存在三维冲突,如图8(b)所示。 表5 上海浦东机场的10次仿真结果统计Tab.5 Result statistics of 10 simulations of Shanghai Pudong Airport 上海浦东机场实际的进场程序如图8(a)中灰色点划线所示,其加权航路长为420.25 n mile;则优化后的进场程序总长度缩短了约6.6%,平均每条进场程序的长度缩短了5.6 n mile。上海浦东机场的日起降约为1 450 架次/天,则其中进场航班数量约为725 架次/天。假设每架航班完全遵循一条进场程序进行进场并着陆,则全部进场航班的总飞行长度减少了4 046 n mile/d。从经济角度分析,这将在燃油消耗费上减少大量开支。以空客A320 机型为例,其在进场过程中的平均油耗为6 kg/km,则总的油耗减少量为4 4954 kg。以2021 年1 月发布的航油价格2.8 元/千克来计算,则优化后的进场程序相较于真实的进场程序要减少约12.6 万元/天的燃油开销,每年的燃油费用可节省约4 600 万元。除了节约燃油成本外,更短的飞行距离有利于减少航空器的尾气排放和噪声污染。在不考虑空中交通拥堵的情况下,应用优化的进场程序,每架航空器对空域的平均占用时间降低,因此有利于提高空中交通运行效率,减轻管制员的工作负荷。 图8 上海浦东机场的仿真结果示意图Fig.8 Schematic diagrams of simulation results of Shanghai Pudong Airport 本文针对机场终端区进场程序规划的模型和算法存在的不足,首先建立了符合区域导航规范的进场程序三维模型,在竖直剖面考虑了处于同一航路的航空器在下降过程中下降角度的差异;其次,给出了表征进场程序汇聚构型的决策变量;最后,提出了基于模拟退火算法与改进A*算法的混合算法,前者主导对汇聚方式决策和汇聚点位置决策的组合优化过程,后者在前者的基础上逐段计算符合约束的最短航路段。基于瑞典阿兰达机场和上海浦东机场的仿真测试表明,算法针对不同的空域布局均能够有效规划多条具有汇聚结构的进场程序,仿真结果在航路总长度和计算耗时两方面较现有相关研究有一定优越性。应用优化的进场程序一方面有利于在战略层面提升终端区空域资源利用效率,另一方面有利于机场和航空公司的节能减排。在后续研究中,将进一步扩展模型和算法,实现对离场程序发散构型的规划,提出一套完整的机场进离场程序优化方法。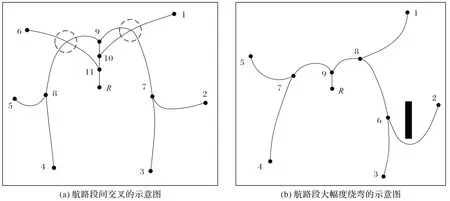
2.2 改进A*算法

3 仿真结果


3.1 瑞典阿兰达机场仿真实验

3.2 上海浦东机场仿真实验

4 结语

