基于E-CARGO模型的开发者推荐方法
李 炜,吴群群,张以文
(安徽大学计算机科学与技术学院,合肥 230601)
0 引言
随着传统开发与互联网协作开发相结合的理念[1]被提出,软件开发不再受限于小型群体,而是延伸到各个开发团队之间的共同协作[2-3],来自不同地域、不同组织的开发者依托互联网为媒介,进行开源软件的在线协作开发[4-7],诞生了以众包[8]、开发者社区为代表的群智协同开发平台。开发者社区将地理位置上分散的开发者和以企业为代表的雇主结合起来,以较少的成本调动丰富的开发者资源。雇主将任务发布到开发者社区,并将任务分解成一系列相关联的子任务集合,在开发者社区进行搜索匹配,最终寻找到合适的开发者完成软件开发任务。以开发者社区GitHub 为例,它拥有超过1 000 万的开发者,共同协作完成了接近4 000 万的软件开发项目[9]。在带来巨大利益的同时,开发者社区庞大的用户、项目等资源数目,不可避免地造成了信息过载问题,使得寻求合适的开发者变得困难。
在此背景下,对开发者能力评估以及开发者推荐技术的研究成为热点。然而,开发者推荐具有新的特征:1)开发者能力具有明显的动态和不确定性;2)软件开发的显著特征是协作性,多个开发者共同协作完成软件开发任务。因此,本文引入模糊评价思想[10],在优化开发者能力评估结果的基础上,将软件开发过程描述为基于角色的协作(Role-Based Collaboration,RBC)[11]问题并对其建模,从而优化开发者推荐结果。
本文的主要工作如下:
1)针对开发者综合能力值的动态性和不确定性,首先,使用模糊层次分析(Fuzzy Analytic Hierarchy Process,FAHP)法构建模糊判断矩阵,得到开发者能力指标权重,进而求得开发者历史综合能力集合;然后,结合云模型理论,利用欧氏距离度量综合能力云模型相似度,求得开发者完成各项任务的综合能力值,最终得到开发者综合能力评估矩阵。
2)将开发者协同开发过程描述为基于角色的协作问题,并使用E-CARGO(Environment-Class,Agent,Role,Group,and Object)模型对其建模,提出了基于E-CARGO 模型的开发者推荐方法。在复杂的约束条件下,通过cplex 优化包对开发者推荐问题求解,最终得到开发者推荐矩阵。
1 相关工作
1.1 开发者推荐
随着互联网协作开发浪潮的兴起,开发者社区资源和人员数量呈指数型增长,造成信息过载,按任务需求匹配合适的开发者变得困难,于是,将推荐技术引入开发者社区应运而生。Sun 等[12]提出了一种名为EDR SI(Enhancing Developer Recommendation with Supplementary Information)的方法,通过考虑开发人员的专业知识和开发习惯来增强开发人员推荐。Zhang 等[13]提出了 DevRec(Developer Recommendation system for open source repositories)混合推荐系统,将基于开发活动的方法和基于知识共享活动的方法相结合,为开源项目推荐合适的开发人员;此外,基于协同过滤(Collaborative Filtering,CF)[14-16]的开发者推荐取得了巨大成功,首先计算待完成任务和已完成任务之间的相似性,然后为待完成任务分配与之相似的已完成任务的开发者。Xie等[17]提出了一种多关系融合的开发者推荐方法,该方法考虑了多元隐式关系,然后基于联合矩阵分解来整合这些关系,并基于深度神经网络来生成推荐结果。Zhang 等[18]提出了一种基于元学习的策略模型,它首先过滤掉那些不太可能参与给定挑战的开发者,然后推荐可能赢得挑战的前k名开发者。现有方法更注重学习开发者的专业能力以及与任务间的交互信息,忽略了开发者之间的协作性,造成任务的整体完成质量不高。为解决开发者间协作性低的问题,弥补任务完成质量不高的缺陷,本文考虑开发者之间的协作性并将开发者协作开发描述为RBC 问题,以优化整体任务完成质量为导向,进行开发者推荐。
1.2 E-CARGO模型
RBC 是一种计算方法,从角色的角度出发,考虑角色间合作及约束条件,使用一系列方法对真实世界的复杂关系进行模拟、分解。2006 年,朱海滨等[11,19]在RBC 的基础上,提出E-CARGO 模型并迅速成为研究RBC 问题中使用最为广泛的框架。E-CARGO 模型将RBC 系统定义为∑::=〈C,O,A,M,R,E,G,s0,H〉,各元素含义为:C是类(Class);O是对象(Object);A是代理(Agent);M是消息(Message);R是角色(Role);E是系统环境(Environment);G是群组(Group);s0是协作系统的初始状态;H是用户。
使用E-CARGO 模型建模RBC 系统的关键在于解决组角色分配问题,即在复杂约束条件下,为角色分配满足需求的多个代理,进而形成一个群组,群组中各代理之间相互协作,共同完成协作任务[11,19-20]。近年来,使用E-CARGO 模型解决组角色分配问题的研究包括:组角色分配(Group Role Assignment,GRA)[20];代理间包含冲突的组角色分配(GRA with Conflicting Agents on Roles,GRACAR)[21];组多角色分配(Group Multi-Role Assignment,GMRA)[22],包含冲突和合作因素的组角色分配[23];树形结构的任务分配[24];考虑代理偏好的组角色分配[25]等。最近,朱海滨等[26]对具有角色和代理双重冲突的组多角色分配(group multi-role assignment with conflicting roles and agents)问题进行了研究。开发者推荐问题的本质,是研究如何将任务分配给合适的开发者,可以转化为组角色分配问题。因此,本文首次将E-CARGO 模型应用到开发者推荐场景中,结合cplex 优化包求解开发者推荐问题。
2 开发者推荐
2.1 问题描述
假设雇主将任务Ω发布到开发者社区。首先,将任务Ω分解成相关联的子任务集合,即Ω={Ω1,Ω2,…,Ωn},Ωn表示第n个子任务,每个子任务由一个或多个开发者来协作完成;然后,从开发者社区获取开发者历史信息,令Λ={Λ1,Λ2,…,Λm},Λm代表第m个开发者,每个开发者一次只能完成一项子任务。令表示开发者Λm完成子任务Ωn的第k个能力指标值。由于每个雇主的要求不同,开发者完成同一项任务获得的评分存在差异,并且不同开发者的能力不尽相同,完成同一项任务的质量也存在差异。因此,针对开发者完成各项任务的能力度量是首要重点。最后,使用E-CARGO 模型建模开发者和任务间的映射关系,求解开发者推荐问题。
2.2 基于E-CARGO的开发者推荐模型
将E-CARGO 模型应用于开发者推荐场景中,重点关注E、C、O、R、A、G六个元素,赋予的实际含义分别为:E表示求解开发者推荐所涉及的各种问题环境;C是一组将概念进行抽象的类,和E关联;O是实例化C的具体对象;R表示开发子任务集合;A是候选开发者集合;G是一个开发组,即完成开发者推荐流程后,所有开发者共同协作完成任务,形成一个开发团队。基于以上定义,使用E-CARGO 进行建模,流程如图1 所示:首先,将任务分解成相关联的子任务集合并发布到开发者社区;然后,搜索候选开发者集合,为每项任务推荐合适的开发者。其中,将任务映射为角色,任务集合Ω={Ω1,Ω2,…,Ωn}对应角色集合R={R1,R2,…,Rn};将开发者映射为代理,开发者集合Λ={Λ1,Λ2,…,Λm}对应代理集合A={A1,A2,…,Am};将开发者完成任务映射为代理扮演角色,开发者能力指标集合SS=对应代理资格值集合VV=。到此,E-CARGO 建模完成。于是,可使用求解组角色分配的方法求解开发者推荐问题,最终通过cplex 得到开发者推荐结果。求解开发者推荐问题还需以下定义:

图1 基于E-CARGO的开发者推荐模型Fig.1 Developer recommendation model based on E-CARGO
定义1任务范围向量L。L是n维整数向量,L[j](0≤j
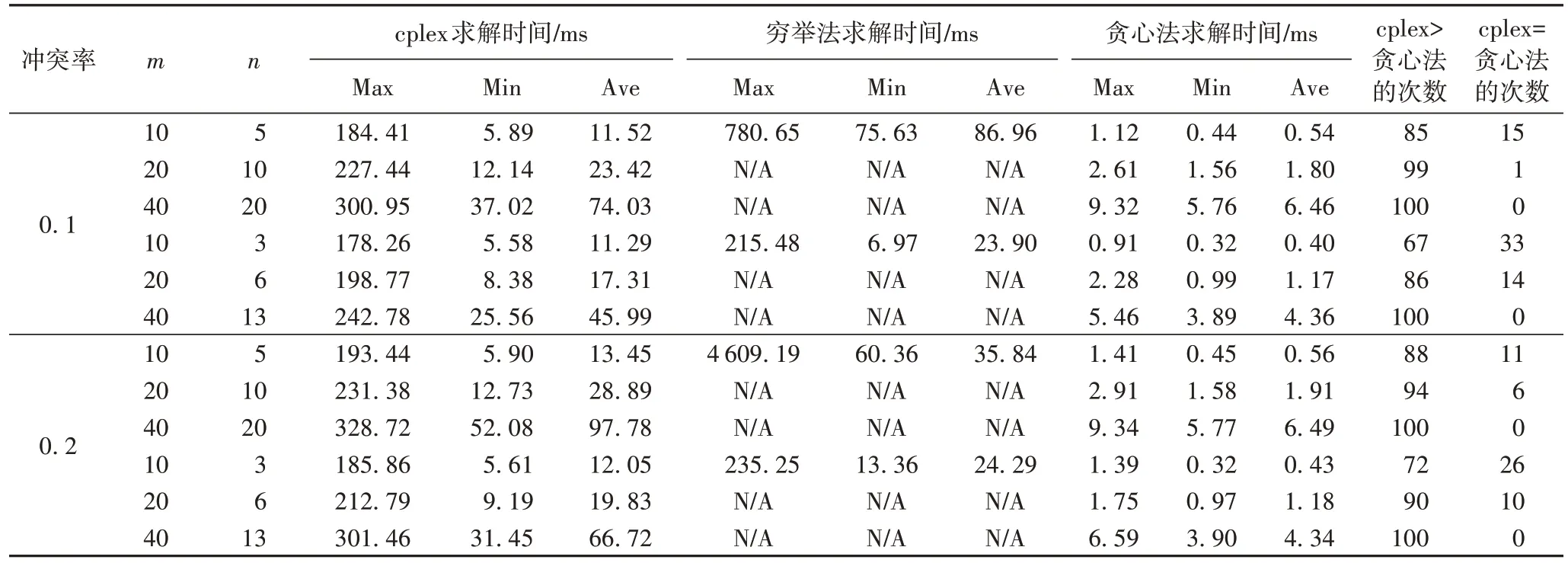
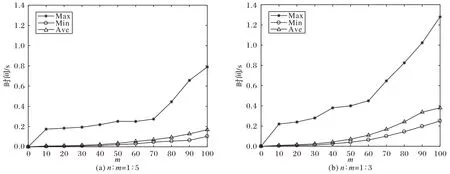
定义2开发者综合能力评估矩阵Q。Q是m×n维的矩阵,Q[i,j](0≤i 定义3任务整体完成质量值ρ。ρ代表开发者之间协作完成各项子任务后的任务总体质量。ρ越大,代表任务完成质量越高。 定义4开发者推荐矩阵T。T是m×n维的矩阵,表示开发者推荐结果,T[i,j](0≤i 定义5冲突矩阵C。C是m×m维的矩阵,C[i,j](0≤i 基于以上定义,开发者推荐问题即求得一个开发者推荐矩阵T。目标函数如下: 其中:式(2)表示开发者只有被推荐和不被推荐两种可能;式(3)表示开发者人数应当满足任务范围向量L的约束;式(4)表示每个开发者一次只能完成一个任务;式(5)表示完成同一个任务的两个开发者应当满足冲突矩阵C的约束。 开发者能力评估矩阵Q的计算过程主要包含两个部分:首先基于各个专家的模糊判断矩阵X,运用FAHP 来计算指标的权重向量W;然后基于云模型理论和权重向量W即可获得开发者能力评估矩阵Q。 2.3.1 基于FAHP的指标权重计算 开发者在项目上的能力体现为不同的度量指标,而每个指标的重要程度明显又是不同的,因此,在对开发者综合能力评估之前,需要先计算各个指标的重要性。本文采用经典的FAHP 方法[10]来计算各项能力指标的权重。FAHP 是层次分析(Analytic Hierarchy Process,AHP)法[27]的一个衍生,是定性和定量相结合的多评价指标优选排序方法。FAHP 方法确定各项指标权重的步骤如下: 步骤1 首先,依托FAHP 方法,根据能力评估的具体任务构建合适的层次模型,即专家对开发者能力量化的依据。如图2 所示,层次模型自上而下分别为目标层、中间层和最低层。其中目标层是开发者能力指标,中间层包括基本指标,任务完成质量指标以及任务完成效率指标,最低层是对中间层的细粒度刻画。然后,专家对n个指标进行评估,即可获得模糊判断矩阵X,其中,X中的元素xij(1≤i≤n,1≤j≤n)是集合{0.1,0.2,…,0.9}中的一个元素。具体地,若xij∈[0.1,0.5),则表示指标i没有指标j重要;若xij∈(0.5,0.9],则表示指标i比指标j重要;若xij=0.5,表示指标i和指标j同等重要。特别地,如果xii=0.5,xij+xji=1,则称X为模糊互补判断矩阵。如果没有特别说明,本文采用的均为模糊互补判断矩阵。 图2 开发者能力指标层次结构Fig.2 Developer ability index hierarchical structure 接下来,根据得到的模糊互补判断矩阵X,即可计算出指标权重,计算公式如下所示: 步骤2 根据等式(6)求得的指标权重W是否合理,还应将模糊互补判断矩阵X与其对应的特征矩阵进行相容性验证。 定义6给定两个矩阵A=(aij)n×n和B=(bij)n×n,规定: 为A与B的相容性指标。 定义7设模糊互补判断矩阵X的权重向量为W=(w1,w2,…,wn),满足wi≥0,=1(1≤i≤n)。则X的特征矩阵W*=定义如下: 在实际问题中,一般由m(m≥2)个专家对某一特定任务进行指标权重评估,建立m个模糊互补判断矩阵Xk=,从而求得对应的指标权重向量Wk=和特征矩阵Wk*。为验证指标权重的合理性,还需完成如下两个步骤: 1)m个模糊互补判断矩阵与其相对应的特征矩阵的相容性验证: I(Xk,Wk*)≤α;1≤k≤m 2)m个模糊互补判断矩阵之间的相容性验证: I(Xk,Xp)≤α;k≠p,1≤k,p≤m 其中:α一般取值为0.1。当满足以上两个条件时,m个指标权重集的均值则可以作为某一特定任务的指标权重值。最终,确定指标权重向量为: 其中:wi=。 举例说明,每完成一项任务,雇主会对开发者的沟通协作能力、专业技能水平、任务完成质量、任务完成效率四个指标进行打分。获取开发者完成某任务的历史能力指标评价集合SS={(0.5,0.5,0.6,0.6),(0.6,0.8,0.8,0.9)},假设通过FAHP 方法计算出指标权重向量W=(0.2,0.2,0.3,0.3),最终,加权求和得到开发者的综合能力集合QS={0.56,0.79}。 2.3.2 基于云模型理论的综合能力评估 在2.3.1 节中,通过FAHP 方法得到了开发者针对某一特定任务的客观合理的综合能力评价集合QS,然而,Q矩阵的建立需要的是单一的综合能力评价值,因此,为了准确衡量开发者Λm对某一子任务Ωn的胜任能力,引入了云模型理论[28-29]。云模型由三个数值特征组成,即期望Ex(expectation)、熵En(entropy)和超熵He(hyper entropy),定义为cm={Ex,En,He}。Ex是综合能力最具代表性的值,En表示综合能力的粒度范围,He描述了综合能力粒度的不确定性。众多云滴组成综合能力云模型,开发者综合能力值可被视为云滴,发送到反向云生成器中,综合能力云模型的三个数值特征可由如下公式计算: 其中:Ex是集合QS的平均值;σ是Ex的标准差;S2是Ex的样本方差;total是集合QS 中的元素个数。为了推荐合适的开发者完成任务,通过计算综合能力云模型间的相似性来识别综合能力差异是至关重要的。本文使用欧氏距离计算相似性,公式如下: 将所有候选开发者的综合能力值转化为综合能力云模型,若历史记录中开发者只完成过一次子任务,则设p为唯一的综合能力值,得到一个具体的综合能力云模型{p,0,0}。因此,对m个开发者进行综合能力评价的云模型矩阵可以描述为: 其中:cmi,j=是开发者Λi对于子任务Ωj的综合能力云模型。由于开发者状态存在波动性以及任务类型的不同,同一开发者执行多次任务会得到不同的综合能力值。而一个好的开发者应当提供稳定的综合能力值。En和He的值越小,综合能力值越稳定,根据这一性质,定义cm+代表最好和cm-代表最坏情况下的理想解: 因此,开发者Λi对于子任务Ωj的胜任能力可用如下公式计算: Q[i,j]的值越大,说明开发者Λi完成子任务Ωj的质量越高,Q[i,j]即作为Q矩阵中开发者Λi完成子任务Ωj的综合能力值。最终,完成Q矩阵的取值。 基于上述分析,解决开发者推荐问题的关键步骤描述如下: 步骤1 确定开发任务的范围向量L,开发者之间的冲突矩阵C。 步骤2 利用FAHP 方法分析指标间的相对重要程度,并根据式(9)计算出开发者能力指标权重,最终加权求和得到开发者历史综合能力评价集合。 步骤3 进一步将开发者综合能力值转化为综合能力云模型,通过式(14)计算出开发者对每个任务的胜任能力,得到开发者综合能力评估矩阵Q。 步骤4 在满足式(2)~(5)的约束条件下求解式(1),最终得到开发者推荐矩阵T。 依据上述步骤,本文使用Java 中的cplex 优化包来实际获得一个开发者推荐问题的解决方案。首先,确定cplex 所需的约束系数、目标函数系数、右侧约束值以及上界和下界。通过Q、L、C、T来定义cplex 中的线性规划问题。其中:T是一个变量,它的上界为1,下界为0。Q是目标函数系数。然后,添加约束和目标表达式,开发者推荐问题的目标应使用矩阵C、Q、T的一维数组形式以及L的线性表达式来描述。伪代码如算法1 所示。 不同于传统的推荐方法,基于E-CARGO 模型的开发者推荐的重点是考虑推荐完成后开发者之间的协作性,即开发者协同合作以求高质量地完成特定的项目。因此,为了解决这一问题,本文考虑了开发者之间的协作性并使用E-CARGO 建模,以优化整体任务完成质量为导向,进行了开发者推荐。通过上述cplex 求解算法可以得到任务完成质量达最大值ρ的推荐矩阵T。 假设某公司向开发者社区发布一项Web 开发任务Ω={Ω1,Ω2,Ω3},共有5 位开发者愿意接受任务,构成候选开发者集合Λ={Λ1,Λ2,Λ3,Λ4,Λ5}。由于Ω1、Ω2任务较重,各需2 人一起完成,任务范围向量L=(2,2,1)。指标集合k={k1,k2,k3,k4},分别表示沟通协作能力、专业技能水平、任务完成质量、任务完成效率。通过开发者社区获取各开发者完成同类任务的历史能力指标评价信息如表1 所示。 表1 能力指标评价信息Tab.1 Ability index evaluation information 为了评估指标权重,公司邀请两位领域专家对各指标进行一一比较,得到模糊互补判断矩阵。由第一位专家给出的模糊互补判断矩阵为: 根据式(6)计算出指标权重向量W1=(0.275,0.225,0.250,0.250),根据式(8)得到X1的特征矩阵为: 由式(7)得到I(X1,W1*)=0.056 <0.1,满足相容性,所以指标权重向量W1的计算是正确合理的。同理,第二位专家给出的模糊互补判断矩阵为: 计算出权重向量W2=(0.275,0.242,0.250,0.233),X2的特征矩阵为: I(X2,W2*)=0.038 <0.1,满足相容性,故W2的计算正确合理。验证X1、X2的相容性I(X1,X2)=0.038 <0.1,满足相容性。最后,综合两位专家的评估结果,根据式(9)确定最终指标权重向量W=(0.275,0.234,0.250,0.241)。对表1 进行加权求和,得到开发者历史综合能力集合如表2所示。 表2 开发者历史综合能力集合Tab.2 Historical comprehensive ability set of developers 根据式(10),计算出各开发者对各子任务的综合能力云模型如表3 所示。 表3 各开发者对各子任务的综合能力云模型Tab.3 Comprehensive ability cloud model of developers for different subtasks 根据式(13),得到综合能力云模型的理想解为:cm+={0.809,0,0},cm-={0.626,0.081,0.03}。再根据式(14)得到开发者综合能力评估矩阵Q如下所示: 另外,考虑开发者之间可能存在的冲突因素,添加冲突矩阵为: 最终,通过cplex 计算出任务完成质量最大值ρ=3.236,得到开发者推荐矩阵T如表4 所示。 表4 开发者推荐矩阵TTab.4 Developer recommendation matrix T 因此,推荐开发者Λ3、Λ5完成子任务Ω1;开发者Λ1、Λ4完成子任务Ω2,开发者Λ2完成子任务Ω3。共同协作,得到最大的任务完成质量ρ=3.236。 为了验证所提方法的有效性和性能,通过使用仿真数据,将本文方法与穷举法及贪心法[21,29]相比较,进行实验分析。本实验在采用Intel Core i5-6200U 处理器@2.3 GHz 和8 GB 内存的联想笔记本上执行,并使用Windows 10 操作系统、Eclipse 开发环境和Java 开发语言。在每一轮测试中,重复实验100 次,每一次的Q、L、C随机生成,并记录下问题求解所花费的最大时间、最小时间、平均时间。实验设定了不同的冲突率、不同的任务数和开发者人数比率,对比本文方法与穷举法、贪心法的求解时间,N/A 表示超过30 min 没有得到结果,同时对比本文方法求解值大于及等于贪心法的次数,实验数据如表5 所示。 从表5 可以看出:随着开发者人数的增加,求解所耗费的时间也在增长。本文方法性能优于穷举法,例如,当m=10,n=5,冲突率为0.1 时,本文方法平均求解时间为11.52 ms,穷举法平均求解时间为86.96 ms。因为穷举法考虑每一步中的所有情况,所以耗费大量时间,并且只有当m=10 时,穷举法才可以在30 min 内获得想要的结果,因此,穷举法不适用于实际的开发者社区中。从表5 还可以看出,随着冲突率的上升,本文方法所耗费的时间也在增加,而穷举法所耗费的时间与冲突率之间没有关联。和贪心法进行对比,由于贪心算法只考虑小范围内的局部最优解,所以求解时间更短,但在ms 的量级上可以忽略不计;而且贪心法获得最优解的次数远远小于本文方法,当问题增大到一定规模时,贪心法并不能获得全局最优解,这说明,本文方法是优于贪心法的。 从表5 还可以发现,随着n∶m的比值增大,问题求解的时间耗费更多,例如,当m=40,n=13,冲突率为0.1(n∶m=1∶3)变为m=40,n=20,冲突率为0.1(n∶m=1∶2)时,本文方法的平均求解时间由45.99 ms 增长为74.03 ms。可见n和m的比值对本实验的性能有很大影响。为了详细研究其影响,设立了两组实验进行对比,每一组的m由10 变为100,步长为10,n和m的比值分别为1∶5 及1∶3,冲突率为0.1,每一组重复实验300 次,实验结果如图3 所示。 表5 本文方法与穷举法及贪心法求解性能对比Tab.5 Solving performance comparison among the proposed method,exhaustive method and greedy method 由图3 可以观察到,随着开发者人数和任务数的增长,求解时间也在增加,说明在实际求解过程中,随着问题规模的增大,所耗费的时间也会增加。同时,当任务数和开发者人数的比率(n∶m)出现增长,所耗费的求解时间也会增加,例如,当m=100,比率由1∶5 增长为1∶3 时,最大、最小、平均求解时间由0.79 s、0.10 s、0.17 s 增加到1.28 s、0.20 s、0.30 s。尽管随着问题规模增大,耗费时间会增加,但从实验结果来看,问题规模即使提升到最大时,所耗费的最大时间也仅为1.28 s,完全在可接受范围内。因此,本文方法能够以较快的速度求得最优的开发者推荐结果,在实际的应用中是有效的且性能良好的。 图3 n∶m不同比值的性能对比Fig.3 Performance comparison of different ratios of n∶m 本文考虑软件开发具有协作性这一显著特点,将其描述为基于角色的协作系统,并使用E-CARGO 模型对其建模,通过E-CARGO 模型中求解组角色分配的方法解决开发者推荐问题,提出了一种基于E-CARGO 模型的开发者推荐方法。首先使用E-CARGO 模型建模开发者与任务间的映射关系,然后结合FAHP 方法和云模型理论计算开发者的综合能力值,最终通过cplex 得到最优开发者推荐结果。在未来的研究工作中,将考虑开发者与任务间以及任务与任务间存在的冲突因素,解决在更为复杂约束条件下的开发者推荐问题。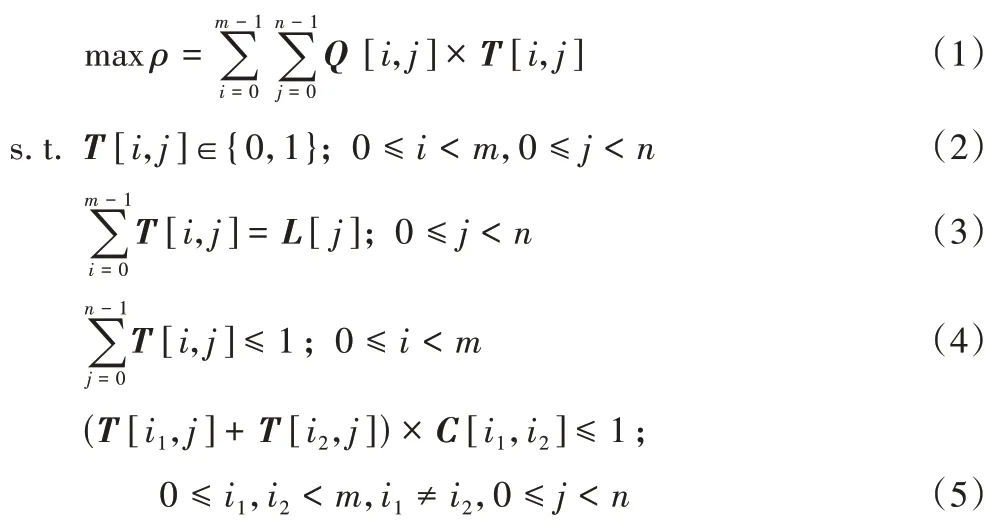
2.3 开发者综合能力评估矩阵Q










2.4 开发者推荐问题求解

3 实验与结果分析
3.1 实例










3.2 实验分析
4 结语

