面向深度学习可解释性的对抗攻击算法

陈 权，李 莉，陈永乐，段跃兴

（太原理工大学信息与计算机学院，山西晋中 030600）

0 引言

深度神经网络（Deep Neural Network，DNN）在计算机视觉、语音识别、自然语言处理等方面取得了巨大成功，但是由于其不透明性，使用者往往在得到决策结果时，却理解不了其预测过程，模型究竟学到了什么有效特征，如何作出预测和判断，整个过程是缺乏可解释性的［1］。

近年来，由于深度神经网络的“黑盒”问题受到了许多学者的广泛关注，解释方法层出不穷，它们在对目标信息进行识别的同时，也会对识别结果进行“解释”，如图1。虽然这种表示方法帮助使用者以人类的认知角度去理解智能机器的推理过程。但是这些解释区域同时也会为对抗攻击带来有利条件。

对抗攻击的目的是对原始图像添加人眼不可分辨的扰动，使得深度神经网络模型进行错误决策。Goodfellow 等［2］曾以一张熊猫照片为例，为其添加微小扰动后成功被模型误分类。许多经典的对抗攻击算法，如BIM（Basic Iterative Method）［3］、C&W（Carlini &Wagner attack）［4］等，它们都基于损失函数的梯度方向进行攻击，梯度的方向决定了对抗样本该如何朝着决策边界移动。文献［5］利用前向导数可以找到能够最大效率扰动样本的输入特征点，但是其计算代价很大，并且准确率低。近些年，一些新的对抗攻击算法，如Ada-FGSM（Adaptive Fast Gradient Sign Method）［6］，它们对原始算法进行了优化，能够根据梯度信息自适应地分配噪声的步长，Superpixel-guided attack［7］则加入注意力机制作为扰动添加的依据。PPBA（Projection &Probability-driven Black-box Attack）［8］和TREMBA（TRansferable EMbedding based Blackbox Attack）［9］的提出，有效减少了黑盒攻击中的查询次数，它们在实验中均有较好的表现。

事实上，本文发现解释方法可以本能地为对抗样本的生成提供特定区域，此外，某些解释方法是基于显著图（Saliency Map，SM）［10］产生，它量化解释区域中每一个像素点，其值的大小代表影响神经网络模型预测结果的程度，故可以利用解释方法定位关键区域，通过显著图进一步细化到其中值最大的像素位置为其添加扰动。基于上述调查，本文对解释方法中的安全性进行了研究。

本文的主要工作为：首先，从众多解释方法中选取了Grad-CAM（Gradient-weighted Class Activation Mapping）［11］作为样例说明，验证了在白盒环境中利用显著图进行对抗攻击的可行性。其次，考虑到目前深度神经网络模型中解释方法的多样性，对于大多数不依赖显著图产生解释区域的解释方法，提出了一种在黑盒环境下的动态遗传算法进行对抗攻击。“动态”强调的是扰动像素数量和扰动值大小的变化关系，通过逐步逼近的方式找到最佳扰动像素集合，即扰动的添加需要多轮遗传算法的支持。相较于传统的遗传算法，本文改进了选择算子，并通过解释区域的变化作为适应度函数引导对抗样本的生成，该方法在不同的神经网络模型中均能以较高的成功率欺骗模型。

1 相关工作

1.1 对抗攻击

文献［12］首先证明了图像中存在着微小的扰动，使得添加扰动后的图像可以欺骗深度学习模型进行错误分类。随后的提出的FGSM［2］、C&W［4］、JSMA（Jacobian-based Saliency Map Attack）［5］、DeepFool［13］等算法都是在模型参数、数据集已知的情况下进行攻击，而在实际情况中，攻击者往往并不清楚模型的结构。文献［14］利用差异进化（Differential Evolution，DE）算法来生成对抗扰动，并且在极端条件下只需要修改图片的一个像素即可完成攻击。文献［15］从一个敌对图片出发，通过拒绝采样，将由敌对初始化的图像逐渐向原始样本靠近，直到找到决策边界，并在决策边界上找到与原始样本最近的对抗样本。下面具体介绍一些经典对抗攻击算法。

1）FGSM。

Goodfellow 等［2］实现了一种高效的对抗样例的生成算法——FGSM，通过在其损失函数相反的方向上添加扰动来实现，其实质是输入图片在模型的权重方向上增加了一些扰动（方向一样，点乘最大），让图片在较小的扰动下出现较大的改变，从而得到对抗样本，ε表示限制扰动范数的超参数，Y为真实标签。公式如下：

FGSM 是通过在增加分类器损失的方向（即一步梯度上升）上迈出一大步来扰动图像。为了避免一次性产生多余的扰动，Kurakin 等［3］提出了BIM，其想法是迭代地采取多个小步骤，控制扰动的大小，同时在每个步骤后调整方向，具体公式如下：

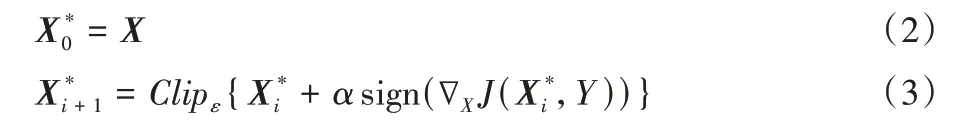
其中：α为步长；Clipε{X′}表示在参数ε下对图像X′裁剪。

2）DeepFool。

FGSM 虽然不需要迭代过程即可计算对抗样本，但是它只是提供了最优扰动的一个粗略估计，并且由于执行梯度的方法，经常得到的是局部最优解。为此，Moosavi-Dezfooli等［13］提出了DeepFool 来获得更小的扰动。该方法是基于超平面分类的攻击方法，如果想改变某个图像的分类，最小的扰动就是将其移动到超平面上，那么这个图像到超平面的距离就是代价最小的距离。

3）One-pixel。

Su 等［14］提出了一种只需要修改图片一个像素的攻击方法，即利用进化算法来生成相应的对抗扰动。这种攻击方式属于黑盒攻击，通过进化算法得到的内在特征，仅需要知道很少的信息，就能够欺骗很多类型的网络。

4）boundary-attack。

这是一种基于决策的攻击，它从较大的对抗性扰动开始，在保持对抗性的同时减少扰动。即在算法中，样本将由初始化的图像逐渐向原始样本靠近，直到找到决策边界，并在决策边界上找到与原始样本最近的对抗样本。同时，与上述的攻击算法相比，基于决策的攻击对梯度防御，内在随机性或鲁棒训练等标准防御具有更强大的潜力。

文献［16］和文献［17］的研究内容与本文很相似，作者利用解释方法与待解释模型之间的不一致性而威胁可解释系统的自身安全；提出了可解释模型的两类对抗样本：1）在不改变模型决策结果的前提下，使解释方法解释出错；2）使模型决策出错而不改变解释方法的解释结果。此外，Ye 等［18］利用显著图的可解释性提出了一种策略来检测敌意示例，如果某实例与图像的激活区域是一致的，则该实例为良性；否则是对抗性的。

本文研究在解释方法环境中如何进行对抗攻击，主要包含如下工作：1）分析了在不同神经网络模型下进行白盒攻击的效果，对失败样本的像素位置选取进行了优化；2）探究了动态遗传算法的收敛性和最优解集，并对比了不同解释方法下生成的对抗样本效果图。

1.2 解释方法

对于目前存在的解释方法可以大致分为以下三类：

1）基于隐层表征的解释方法。这类解释器利用DNN 中间层的特征映射来生成属性映射。其中Grad-CAM 是这类的代表性解释方法。该方法利用加权梯度类激活映射，使任何目标特征的梯度经过最后一个卷积层后产生大致的局部特征统，显示出图像中对目标预测分类重要的区域。值得注意的是，除了直接生成解释图之外，Grad-CAM 还可以与其他经典的显著图方法相结合，得到点乘后的Guided Grad-CAM 图。

2）基于模型指导的解释方法。模型引导的方法不依赖于中间层的深层表示，而是训练元模型来直接预测单次前馈传递中任何给定输入的解释图。本文认为RTS（Real-Time Saliency）［19］是这类方法中的代表性方法。

3）基于摄动引导的解释方法。通过以最小的噪声扰动输入并观察模型预测的变化来制定寻找解释图的方法。其中较为典型方法为Fong 提出的一种通用框架［20］，用Mask代指。

上述解释方法的结果如图1 所示，并且本文将解释方法为图片做出的解释称为解释图。

图1 不同解释方法的解释区域Fig.1 Interpretation areas of different interpretation methods

1.3 显著图

显著图的提出是为了解决DNN 图像分类模型的可视化问题。Simonyan 等［10］认为显著图是衡量图片X的某个像素点对分类c的评分函数Sc(X)的影响；并且通过计算一阶泰勒展开式将线性模型扩展到了复杂模型中，让其在X的邻域内用线性函数近似Sc(X)。即：

其中：wc和b分别是模型的权重向量和偏差。则Sc相较于图像X在点xi处的导数为：

计算wc其实是在整个网络进行反向传播，也就是计算输入X的梯度（梯度即表示变化最快的方向）。相较于绝大多数的对抗攻击都依赖损失函数产生对抗样本来说，显著图虽然在扰动的添加方向上优势较弱，但却以视图的方式可以呈现出针对不同目标类别的显著图，进而可以与解释方法联系起来。此外，文献［21］优化了显著图在反向传播中经过ReLU（Rectified Linear Unit）层的处理策略，提出了导向反向传播，它与普通反向传播不同，得到的显著图基本没有噪声，而且使特征很明显的集中在物体部位上。文献［22］也将改进后的显著图用在解释方法中。

2 本文算法

2.1 算法原理

白盒攻击原理：1.3 节中介绍的显著图式（4）可以理解为：梯度的大小表示某个像素点改变后对预测结果的影响。即值越大的像素位置，添加相同的扰动量越过决策边界的可能性越大，所以有如下公式：

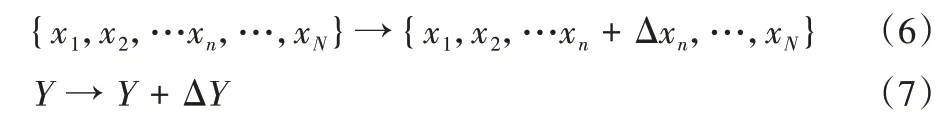
其中：Δxn表示为图像xn位置添加的扰动；ΔY为预测结果发生的变化。如果试图通过改变一个像素位置来翻转Y，类如One-pixel 攻击，那么修改后像素位置极其明显，而且扩展到分辨率更高的图片中，只针对一个像素位置的攻击很难成功。故本文算法通过与显著图的结合来生成对抗样本。

利用全部的Guided Grad-CAM 图中信息生成对抗样本，即扰动添加策略为整个解释区域中显著图相对应的位置。详细过程在算法1 中给出。

黑盒攻击原理：Grad-CAM 由于其特殊性（模型的解释是基于显著图）在白盒环境中有较好的表现。为使攻击更具一般性，需要进一步探讨不同解释方法下给出的解释图该如何有效添加扰动。本文发现，白盒实验中每次为图片加入轻微的扰动后，其解释图均会发生变化，而产生这种现象的原因在于决策空间中的任意一个状态均对应一个解释图（本文称在某一网络模型下图片X的所有决策状态所对应的解释图集合称为解释空间）。即当对抗样本进行像素点修改时未使标签发生翻转时，解释图仍将随之改变，因此通过这种关系能够推测对抗样本在决策空间的移动。

简单地使用遗传算法来寻找最优的像素位置是低效率的，因此，本文提出了一种动态的遗传算法来生成对抗样本，即在多轮的遗传算法中，某一扰动值下的初始扰动像素点的生成会基于较大扰动值下得出的最优扰动解，随着扰动值减小，扰动像素点集合不断增加，直至结果集使预测标签发生改变。具体来说：

1）适应度函数为D，该轮的扰动系数为θ，随机生成规模为N的初始种群在迭代次数内进行遗传算法L，记录找到最优解的像素位置Γ。如果某次的遗传算法改变了预测标签，则提前结束本轮的遗传算法，减小扰动值θ，进行下一轮遗传算法。

2）在Γ像素位置的基础上添加N个位置，继续使用L找到当前扰动值下的像素位置Γ（当前值为2N），θ减小。以此循环，直至找到最佳的扰动像素位置使原始标签Y发生改变。具体过程详见算法2。

2.2 收敛性和最优扰动集合分析

文献［23］对标准遗传算法（Conventional Genetic Algorithm，CGA）的收敛性有以下结论：

定理1CGA 不能收敛至全局最优解。

定理2带有最优保持操作的遗传算法一定收敛至全局最优解。

为使每次迭代中保留最优个体，本文对遗传算法中的选择算子作出了优化，在使用“精英保留”策略时考虑到每一张图片的显著图均集中在物体轮廓周边这一事实，给出新的适应度函数公式：

它由两部分构成：

1）相似性度量：

2）固定半径几何分形描述点的分布情况。

其中：ω1和ω2为权重系数，本文分为别0.8 和0.2。

由定理2 可知，在不同扰动值下的遗传算法一定会收敛，同时，得到的扰动集合也是最优的。但是，随着扰动值不断减少，扰动像素集合每次线性增加N，最终解集对于对抗样本却不是最优解。因为N是一个区间，某一次集合的改变极大概率会超过最优解集的个数，理论上当N为1 时，每次减少扰动值时只增加一个像素点位置，当满足不超过最大失真阈值时，得到像素集为最优扰动集合。但如此解决问题会花费大量的时间。如图6 所示，修改像素数量N的值与迭代次数成指数关系。因此，在保持较高攻击成功率的情况下，选取最少迭代次数相对应的修改像素数量作为增量N生成的扰动集合也可以当作最优解。

2.3 性能分析

为描述动态遗传算法的时间复杂度，本文计算了其运行时间，同时对比了与灰狼算法、布谷鸟算法和樽海鞘群算法的性能优劣。在VGG-19 模型中选取了CIFAR-10 数据集［24］100 个图片样例进行对抗攻击，标准函数选取式（8）。实验数据如图2 所示。

图2 迭代收敛图Fig.2 Iterative convergence graph

动态遗传算法在迭代次数为110 时已经收敛，同时有效使预测标签发生翻转的个数多达93 例，明显优于其他算法。并且由表1 可知，本算法的运行时间少于灰狼算法和布谷鸟算法，虽然樽海鞘群算法的运行时间最少，但对抗攻击的效果却不如动态遗传算法。

表1 不同优化算法的运行时间Tab.1 Running times of different optimization algorithms

3 实验与结果分析

本文采用ImageNet 数据集［25］来评估实验，它由来自1 000 个类的120 万张图像组成，每幅图像都被居中裁剪到224×224 像素，随机抽样1 000 个由模型正确分类的图像作为实验测试集。

本文讨论的攻击只针对无目标设置，即添加的扰动将原始样本的标签翻转到任何其他标签即可。为衡量攻击的性能，本文定义攻击成功率为：

因为在基于Guided Grad-CAM 图添加扰动时，无法确定扰动的方向，所以本实验分别讨论了不同S（S=-1 或者S=1）下的攻击情况。

3.1 白盒攻击

为实例化DNN 模型，本文将Grad-CAM 解释方法部署在由pytorch 提供的预先训练的网络VGG-19［26］、ResNet-50［27］和SqueezeNet［28］和AlexNet［29］中，并严格定义对抗样本的产生，同时将每种攻击的最大迭代次数固定为80 次，扰动系数θ设置为0.01。

表2 总结了在Grad-CAM 解释方法下对不同DNN 模型的攻击成功率与BIM、DeepFool 攻击算法的对比情况。如图3所示，在ResNet-50 模型下使用算法1 确实产生了对抗样本，并且其扰动量更少，扰动位置更精确。原始图片的预测真实值由287（猫）在添加扰动后，变为了104（袋鼠），原因在于显著图和解释区域同时限制了扰动添加的区域范围，所以使攻击更具针对性。文中以不同的背景颜色分别表示S=1 和S=-1 的情况。

表2 不同模型下的无目标攻击成功率 单位：%Tab.2 Untargeted attack success rate under different models unit：%

图3 算法1下的攻击结果Fig.3 Attack result graphs under algorithm 1

但是对同一图片的解释区域增加或减少噪声均可以成功欺骗模型的例子并不多。实验发现S=1 时的成功率普遍高于S=-1 时的情况，在图4 中，具体展示了ResNet-50 模型下的对抗样本生成情况。其中：S=1 时超过47%的样本只需10 次以内迭代次数就可以成功误导DNN 模型；而S=-1时的效果并不好，这可能是因为降低像素会减少输入图片的信息，让网络难以提取特征，也难以进行分类。此外，不同模型下的实验结果差距较大的原因在于不同模型的鲁棒性不同。以下实验默认均基于S=1 的条件下添加扰动。

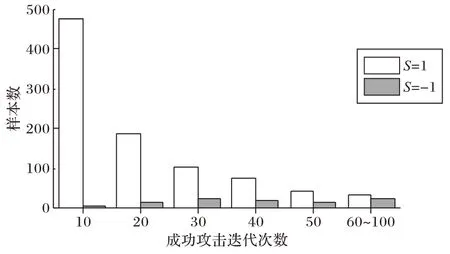
图4 样本成功攻击迭代次数分布Fig.4 Distribution of iteration numbers of sample successful attack

接着讨论几张攻击失败的图片，如图5 所示，它们的失败是由于扰动量超过了最大失真值，可以观察到对抗样本相较于原图片增添了许多深色像素点，这是由于：1）待识别物体几乎占据了整个图片的大小，在此基础上得到解释方法下的显著图同样很大，这与不使用解释方法得到的显著图差别很小；2）不同显著图方法下得到图片细腻度不同，如图5 中得到的显著图有许多不同程度的模糊区域。因此，攻击失败的根本原因在于扰动的添加无法真正集中在重要的像素位置集合中。每次添加像素的位置均包含了显著图中的较小值，虽然它们对结果有影响，但不是起决定性的，众多的较小值影响了攻击效果。

图5 攻击失败结果Fig.5 Attack failure results

为使添加噪声的数量可以更精确，本文改进了算法1，最直接的方法是减小解释图的解释区域，但不同的解释方法计算得出的解释区域难以统一，反观不同模型下的目标显著图却是确定的，故给出式（12）选取扰动位置：

该公式表明每次迭代从显著图中挑选出值最大的前n个位置为图像I添加扰动，如果图中某一点的扰动量超过了最大失真阈值ϒ，则重新选取下一个较大值。

实验结果如图6（a）所示。随着修改像素位置集合N的不断缩小，攻击成功率逐渐提高，并且达到90%以后的变化不再明显，结合图6（b），实验在获取更加精确扰动的同时迭代次数成倍增加。表3 展示了每次修改图片像素数量为50情况下的攻击数据，攻击成功率均达到了90%以上。

表3 改进后不同模型下的无目标攻击成功率 单位：%Tab.3 Untargeted attack success rate under different models after improvement unit：%

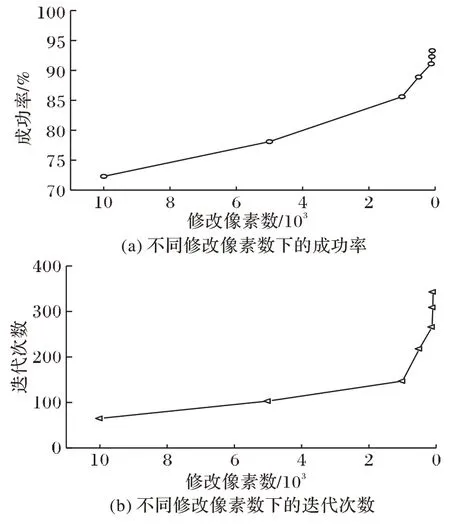
图6 不同修改像素数量下的成功率和迭代次数的关系Fig.6 Relationship between success rate and iteration number under different numbers of modifiedpixels

本文具体分析了改进后的攻击过程，如图7 所示，在给定N为20 的情况下，随着每次为图片添加显著值最大的像素位置，噪声逐渐聚集在物体的轮廓上，并且解释图也在发生变化。算法1 改进后产生的扰动数量更少，分布也更加集中，同时预测结果不再依赖于非必须像素位置，扰动值也随之减小。

图7 迭代攻击过程Fig.7 Iterative attack process

3.2 黑盒攻击

算法2 介绍了为图片添加扰动的主要思路，但在实验中，本文改进了算法2，因为在对图像I添加不同的扰动后，其解释图会相应出现不同的解释区域。为选取最佳的候选扰动像素区域，本文对解释空间进行了探讨，希望解释图在解释空间中尽可能朝向它的边界方向移动，而不是任由其在解释区域中随意移动，如图8 所示。然而，对于如何选择每次移动的方向，本文在图9 中以二维平面进行说明，如果一个点连续移动两次，第一次移动后的位置与初始点之间的距离d1，大于第二次移动后的位置与初始点之间的距离d2，则认为两次移动的方向发生了严重变化。即在选择当前解释图变化最优值的同时也会考虑上一次解释图与当前解释图的像素变化情况。

图8 解释空间和决策空间示意图Fig.8 Schematic diagram of interpretation space and decision space

图9 二维平面上点的移动示意图Fig.9 Schematic diagram of movement of a point on two-dimensional plane

本文实验参数设置如表4 所示，在N为18 时，对比了1.2节中三种解释方法下的黑盒攻击效果，如图10 所示，同一图片产生了不同扰动，本文认为是由于解释器方法与模型的不一致性所导致，即某一方法的解释只能解释部分模型的行为。

图10 不同解释方法下的扰动结果Fig.10 Disturbance results under different interpretation methods

表4 参数设置Tab.4 Parameter settings

MASK 侧重于输入-预测对应，而忽略了内部表示；CAM利用了中间层的深层表示，而忽略了输入-预测对应；RTS 使用辅助编码器的内部表示和训练数据中的输入解释对应，但这可能会偏离DNN 的真实行为。因此即便对于同一图片，不同解释方法产生的对抗样本也会略有不同；同时扰动也全部集中在重要区域，均使网络模型给出错误预测。

此外，本文以Grad-CAM 解释方法为例，对比了五种同样是黑盒攻击的算法One-pixel attack、boundary attack、Ada-FGSM、TREMBA 和PPBA，其中对One pixel 算法中攻击的像素个数增加至5 个，因为在ImageNet 数据集中使用一个像素攻击的成功率太低。实验结果如表5 所示。

表5 不同模型下的黑盒攻击成功率 单位：%Tab.5 Black-box attack success rate under different models unit：%

本文提出的黑盒攻击算法在不同网络模型中有较好的攻击效果，结合表6，平均攻击成功率高于Ada-FGSM 3.18 个百分点，高于PPBA 8.63 个百分点，此外，尽管One pixel 的运行时间较少，但攻击成功率却降低了16.53 个百分点，TREMBA 攻击成功率高于本文算法，但该算法需要额外训练编码器-解码器产生对抗扰动，同时消耗的时间为1.6 倍。本文认为略差于Boundary-attack 的原因在于：1）早熟。这是遗传算法最大的缺点，即对空间的探索能力是有限的，容易导致收敛至局部最优解，类似如图4 中白盒攻击出现的问题。2）虽然改进了选择算子，但对于交叉率和变异率参数，目前的选择大部分是依靠经验。3）解释方法到目前为止，并没有一个权威的性能评价指标，无法衡量一个解释方法的好坏，也就出现不同的解释方法得到攻击成功率存在差异。此外模型的泛化性与可解释性之间始终存在一个平衡，泛化性好的网络模型透露的信息越少，也越难以捕捉到有用的信息。

表6 平均50张图片的处理时间 单位：sTab.6 Average processing time of 50 images unit：s

除此之外，本文在表7 中还对比了不同关键参数下的实验效果。组1 为本文实验参数，如果只考虑高性能，如组2，减少修改像素位置的代价是巨大的，其运行时间增长了接近两倍，但成功率仅仅提高了1.32 个百分点。同时，扰动系数决定了步长的大小，能够提高求解的速度，但过大会越过最优解，如组3。因此，本文综合考虑时间复杂度和成功率的情况，从众多参数指标中挑选出了较为合理的取值。

表7 参数性能对比（SqueezeNet）Tab.7 Performance comparison of different parameters（SqueezeNet）

最后本文解释了算法对初始值的依赖问题。不同像素数量相对应下的遗传算法，均会在上一次的最优解中随机添加新的像素位置，即便不同的像素位置得到不一样的结果集合，没有找到最优解集，仍不会影响最后的结果，因为之后新添加的像素点会在适应度函数的约束下沿着上一轮错误标签的方向移动，直到越过决策边界。最优解的出现会加快算法的运行。对于神经网络模型来说，单独讨论某一像素点的增加和消失是没有意义的，决定预测结果的是像素点之间的空间关系。

4 结语

本文讨论了深度学习中解释方法存在的安全性问题，即依据显著图为图片添加扰动后可以成功欺骗神经网络模型，除此之外，利用解释图与决策空间的联系，可以评判扰动对预测结果的影响，因为解释图比预测结果的变化更加敏感细腻。当图片被添加轻微扰动时，解释区域会随之改变但是预测结果却未发生改变。正是基于这种联系，本文提出了一种动态的遗传算法产生对抗样本，通过在不同神经网络模型下测试验证，实验数据均到达预期结果。由此可见，解释方法虽然作为一个新领域受到了不少学者的追捧，但同时也带来了危险，它给出了模型本身之外的信息，使恶意图片的生成更加简单，攻击方式也更加多样化。

此外，本文并没有在白盒环境中进行目标攻击实验，因为在JSMA 攻击中已经提及了类似的算法。在黑盒实验中，虽然实验成功率较高，但是运行时间却与其成正比，多轮的遗传算法占据了大部分时间。

最后仍需指出两点值得继续研究的问题，首先对于图片噪声添加的取值S并没有深入研究，S=1 时结果更优的事实还需进一步解释。其次是否还存在一些更好的算法能够在有效降低时间复杂度的同时保持最优解也值得进一步研究。