近似概念的遗传生成算法及其推荐应用

刘忠慧，王梓宥，闵 帆，2*

（1.西南石油大学计算机科学学院，成都 610500；2.西南石油大学人工智能研究院，成都 610500）

0 引言

形式概念分析（Formal Concept Analysis，FCA）［1］是一种在形式背景上进行的数据分析与规则提取方法，近年来被广泛应用于机器学习、数据挖掘、知识发现等领域。形式背景包含了对象、属性以及它们之间的二元关系，由形式背景生成的概念是对象集合与属性集合组成的二元组，包含了二者之间的对应关系，能很好地描述推荐系统中用户的消费记录或偏好，因此FCA 被引入推荐系统当中。

由于形式概念的定义非常严格，在形式背景中存在许多不完全满足该定义，但有实际意义的二元组，因此有研究者通过弱化概念生成中的条件提出近似概念［2-7］。范妍等［4］提出k级近似概念的相关理论知识，Li 等［2］研究了近似概念的构建及其在知识约简与规则获取领域的应用。然而，这些研究处于理论阶段，还未与推荐系统结合。

概念格［1］是将形式概念通过偏序关系连接起来的格结构。FCA 应用于推荐系统的最初方案是构建概念格，根据概念格中的层次关系向目标用户进行推荐［8］。概念格构建［9-10］方式主要有批处理式构造算法、渐进式构造算法以及并行算法［11］，但其时空复杂度都会随着形式背景的规模增大而急剧增加。推荐系统的实际应用场景往往面临的是大规模数据集，因此概念格在推荐系统中的应用受到了限制。

针对该问题，刘忠慧等［12］提出了利用启发式信息生成概念集合代替概念格进行推荐应用。启发式概念构造的组推荐（Group Recommendation based on Heuristic Concept set，GRHC）算法利用面积作为启发式信息，生成包含每一个对象的概念集合，实施推荐。该算法与概念格推荐算法的效果相当，算法运行效率远优于后者。但GRHC 算法只考虑了面积约束，忽略了相似度和近似概念的作用。

本文提出基于遗传算法的近似概念生成算法（Approximate Concept Generate Algorithm，ACGA）及其推荐应用方案。首先利用启发式方法生成初始概念集合；其次以外延相似度以及外延与内涵阈值为约束条件，对概念进行交叉、选择及变异操作，得到近似概念；最后根据邻居用户的偏好，向目标用户进行个性化推荐。本文工作的优势主要表现在两方面：一方面，启发式概念集合生成保证了较低的时间复杂度；另一方面，近似概念提升了推荐的精度。

1 相关工作

本章给出形式概念分析以及遗传算法的基本概念。

1.1 形式概念分析相关知识

定义1形式背景［1］。三元组T=(G，M，R)为一个形式背景，其中：G是对象的集合；M是属性的集合；R是G和M之间的二元关系，R⊆G×M。若(g，m)∈R，记为gRm，表示对象g拥有属性m。

对对象集X⊆G和属性集B⊆M，分别定义如下运算：

表1 是一个简单的形式背景，记录了10 位用户对7 部电影的观看情况。若用户ui(0≤i≤9)观看过电影mj(0≤j≤6)，则(ui，mj)=1；反之(ui，mj)=0。

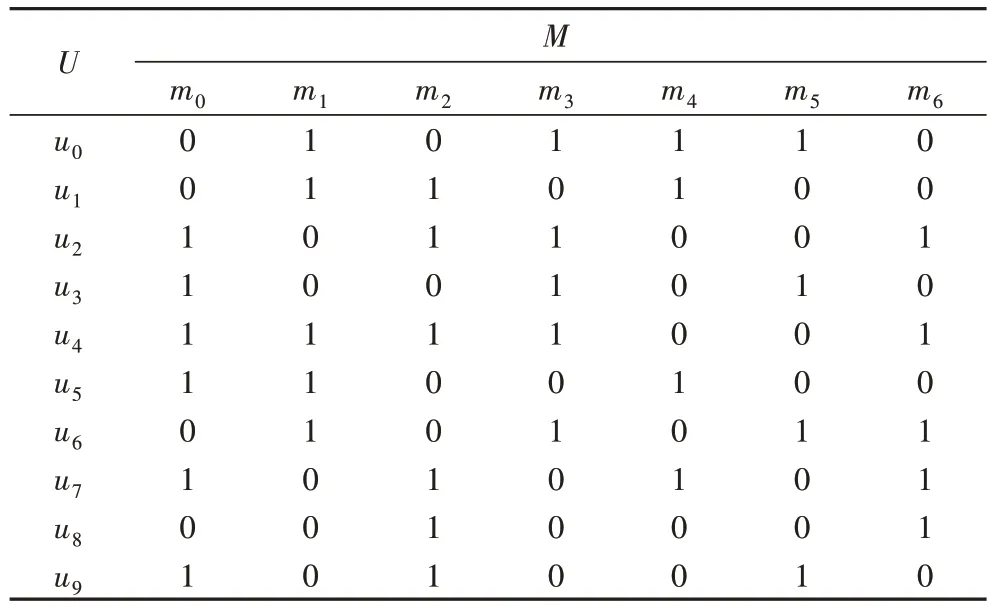
表1 一个形式背景的例子Tab.1 Example of formal context

定义2评分形式背景［13］。三元组O=(G，M，S)为一个评分形式背景，其中：G是对象集，M是属性集，S是对象对属性的评分数据。

表2 是一个简单的评分形式背景示例，其中记录了10 位用户对7 部电影的评分情况，分值范围为0～5。若用户ui(0≤i≤9)观看过电影mj(0≤j≤6)，则(ui，mj)表示用户ui对电影mj的评分，(ui，mj)=0 代表用户ui未观看过电影mj。

表2 一个评分形式背景的例子Tab.2 Example of scoring formal context

定义3形式概念［1］。在形式背景T=(G，M，R)中，令E⊆G，I⊆M，若二元组(E，I)满足E*=I，I*=E，则称(E，I)为形式背景T的一个形式概念，简称概念。E称为概念的外延，I称为概念的内涵。

C=({u2，u3，u4}，{m0，m3})为表1 所示形式背景的一个概念，其中{u2，u3，u4}为外延，{m0，m3}为内涵。

定义4偏序关系［1］。给定形式背景T的概念C1=(E1，I1)和C2=(E2，I2)，若E1⊆E2(⇔I1⊇I2)，则称C1为C2的子概念，记作C1≼C2，显然，“≼”定义了概念之间的一个偏序关系。

定义5概念格［1］。在形式背景T=(G，M，R)中所有概念通过概念之间的偏序关系构成的格结构称为概念格，记为L(G，M，R)。

定义6近似概念［4］。给定形式背景T=(G，M，R)，二元组P=(E，I)，由定义2 可知若E*=I，且I*=E则二元组P称为T中的一个概念；相反地，若E*=I但I*≠E，则二元组P称为T中的一个近似概念。

1.2 遗传算法相关知识

遗传算法［14-15］是一种基于自然选择和遗传机制的随机搜索算法。遗传算法对自然选择和自然遗传过程中的繁殖、交叉和变异进行了模拟。在每一次的迭代过程中均按照某种指标对当前种群进行筛选，保留较优个体，再利用交叉、变异、选择算子产生下一代种群，重复直到满足某种收敛指标为止。

概念的生成过程与此类似，需要外延对象相似度高，同时内涵具有一定规模。交叉、变异操作会增加更多样性的概念，包括近似概念，丰富概念集合。杜鹃等［16］利用遗传算法生成了概念集合，证明了遗传算法可以应用到概念生成过程中。

1.3 推荐系统相关知识

当今时代，互联网联系着人们生活的方方面面，也因此使人们进入了一个大数据时代。在规模庞大的数据中，用户如何快速获取有用信息成为一个待解决的问题。推荐系统［17-18］为该问题提供了一个高效的解决方案。组推荐［19-20］、社会化推荐［21-22］等方法都为用户提供了高效准确的推荐方案。同时，利用形式概念分析进行推荐［23-24］，也是一种有效的解决方案。

2 问题分解

本章主要介绍近似概念生成及推荐过程所涉及到的两个子问题：一是基于遗传算法构造近似概念集合；二是利用近似概念进行推荐。

2.1 近似概念集合构造

在对该问题进行描述之前，先给出该问题所涉及的相关定义。

本文利用用户之间的距离表示用户相似度，定义如下：

定义7用户相似度。给定评分形式背景O=(G，M，S)，用户ui，uj∈G，则ui，uj基于M的相似度计算公式定义如下：

其中：mk∈R，R为用户ui、uj共同拥有的项目集合；s(u，m)表示在形式背景O中对象u对于属性m的评分。特别地，若i=j，simM(ui，uj)=0。

由定义7 可相应地给出外延相似度的计算公式如下：

其中：uk∈E-{u}。

问题1 基于遗传算法的近似概念集合构造。

输入 评分形式背景O=(G，M，S)，初始概念集合CR。

输出 近似概念集合SP。

约束条件 ∀C1，C2⊂CR，u∈C1∩C2，simP(u)≥。

优化目标 max(simP(u))。

约束条件表示得到的近似概念P的外延相似度至少应大于或等于参与生成的原概念外延相似度的最小值；优化目标为近似概念的相似度最大。

2.2 基于近似概念的推荐

为推荐更加准确，给出推荐置信度的定义如下：

定义8推荐置信度［12］。给定形式背景T=(G，M，R)，其中的一个概念C=(E，I)，x∈E，r(x，i)=0，则基于概念C向x推荐i的推荐置信度计算公式如下：

问题2 基于近似概念的推荐

输入 评分形式背景O=(G，M，S)，近似概念集合SP，推荐阈值α。

输出 推荐矩阵L。

约束条件 ∀(E，I)∈SP，∀u∈E，m∈M-I满足向u推荐m的用户数量在该概念的外延长度中所占比例不低于α。

优化目标 max(F1)。

约束条件表示向用户进行推荐时，外延中拥有待推荐项目的用户数量应大于推荐阈值；优化目标为推荐时的F1 值最大化，以达到更好的推荐效果。

3 方案与算法设计

本章针对上述问题，给出了相应的算法方案以及伪代码描述，最后对算法的复杂度进行了分析，并给出了一个算法运行实例。

将遗传算法引入概念生成，需要对交叉、选择和变异算子根据算法方案进行重新定义。

定义9交叉算子。设C1=(E1，I1)，C2=(E2，I2)是形式背景T中的两个概念，且E1∩E2≠∅，交叉算子cross 的计算为：

式（6）对两个概念的外延求交集，得到新外延后更新内涵。

定义10选择算子。设P=(E，I)是形式背景T的一个近似概念，且u∈E，λ为外延相似度阈值，α为内涵阈值，β为外延阈值，SP为近似概念集合，选择算子select 的计算式为：

满足外延相似度阈值、外延个数和内涵个数的近似概念P被选中。

定义11变异算子。设P=(E，I)是形式背景T的一个近似概念，且u∈E，若u′满足max(simM(u，u′))，则变异算子mutate 的计算为：

根据相似度为近似概念的外延添加新用户。

3.1 近似概念集合生成算法

近似概念生成算法（ACGA）是在启发式方法［12］生成的概念集合上进行操作，包含两个子算法：算法1 对概念进行交叉和选择运算，算法2 对概念进行变异和选择运算。

启发式算法以每个对象为代表，逐一添加属性到内涵中，直至概念面积不再增加，生成了新概念。

算法1 对两个概念进行交叉运算。SPC为变异运算概念候选集，SP为近似概念集合。首先在包含用户u的概念集合Cu（Cu⊆CR）中选取两个概念Ci、Cj，对其外延取交集，见算法第4）行。接着，根据取交集得到的用户集合E来更新内涵，得到I，见算法第5）行。若P满足外延相似度大于Ci、Cj外延相似度的最小值且其内涵与外延长度均满足阈值，则存入SP；否则，将其存入SPC中进行下一步操作。

算法2 对算法1 得到的变异运算候选集进行变异操作。第3）行表示对形式背景中的对象按用户相似度降序排列并存入Du。向P′的外延依次添加Du中的用户u′，见算法第5）～7）行。每添加一个用户计算一次外延相似度，见算法第10）行。若外延长度达到阈值或外延相似度不再增加，则存入SP。

3.2 基于近似概念集合的推荐算法

基于近似概念集合的推荐算法（Recommendation method based on Approximate Concept Set，RACS）是基于所有包含用户u的近似概念，向用户u推荐其未拥有的项目。第5）行表示对于u未拥有的项目m，若基于近似概念P得到的推荐置信度大于推荐阈值γ，则向用户u给出对于项目m的推荐。

3.3 时间复杂度分析

下面对算法1、算法2 进行时间复杂度分析。假定形式背景的规模为n×m，即其中有n个对象、m个属性。在算法1 中，对两个概念外延进行交叉操作时，最坏的情况就是参与交叉的两个概念的外延长度均为n，因此交叉操作的时间复杂度为O(n3)；算法2 中变异操作的最坏情况就是对一个长度为n的外延的每一个位置都进行变异，则其时间复杂度为O(n2)；算法3 中利用近似概念为每一个用户进行推荐的时间复杂度为O(n2m)，则算法的总时间复杂度为O(n3+n2m)。但实际应用中属性个数小于对象个数，包含相同对象的概念数远小于n，因此算法的时间复杂度小于O(n3)。

3.4 运行实例

下面以表2 所示的形式背景为例，描述针对用户u2的近似概念生成以及推荐过程。其中外延阈值β=4，推荐阈值γ=0.5。

在表2 所示的形式背景中，以启发式方法为每个用户生成相应的概念，u2参与生成的其中两个概念分别为C1=({u2，u3，u4}，{m0，m3})，C2=({u2，u4，u7}，{m0，m2，m6})。首先对C1和C2的外延求交集，得到E′={u2，u4}，接着根据E′更新内涵，得到I′={m0，m2，m3，m6}，由此得到用户u2的一个候选 近似概念P=({u2，u4}，{m0，m2，m3，m6})；接下来计算P的外延相似度simP(u2)=1.5，而=1.5，=1.9，近似概念P满足相似度不小于C1或C2，但由于概念P的外延长度小于外延阈值，因此需对其进行变异操作。按照用户相似度降序排序，首先向P的外延E中添加1 号用户，得到E={u1，u2，u4}，由此得到内涵I={m2}，此时P=({u1，u2，u4}，{m2})，且计算可得simP(u2)=2；继续向E中添加9 号用户，得到E={u1，u2，u4，u9}，由此得到I={m2}。此时P=({u1，u2，u4，u9}，{m2})，计算可得simP(u2)=2.33；若再继续向E中添加用户，得到的内涵长度将变为0，因此停止添加。至此，得到用户u2的一个近似概念P=({u1，u2，u4，u9}，{m2})。重复上述过程可得到每一个用户的近似概念。

以近似概念P向用户u2推荐m1为例描述推荐过程。在概念P中，用户u2的邻居用户为u1、u4、u9，其中用户u1、u4观看过电影m1，因此cfP(u2，m1)=0.67，大于推荐阈值，因此向u2推荐m1。

4 实验与结果分析

4.1 实验数据集

实验数据集采用ML-100K（Movielens-100K）、ML-1M（Movielens-1M）、EachMovie、Jester，以及它们的抽样数据集，并在实验中将每一个数据集都划分为训练集及测试集两个部分，其中80%数据作为训练集，20%数据作为测试集。表3 是四个数据集的详细信息。

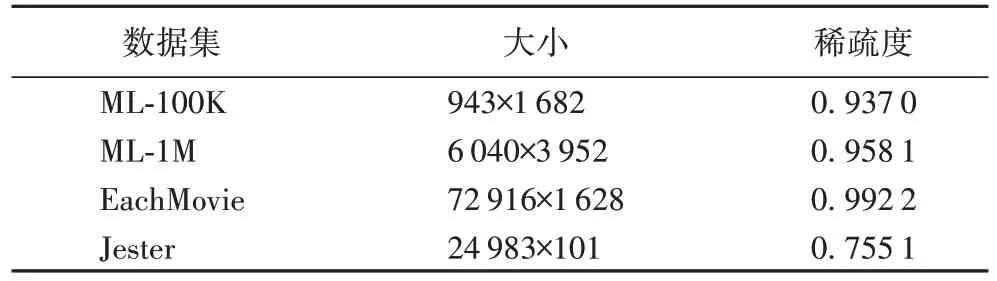
表3 实验数据集Tab.3 Experimental datasets

4.2 推荐效果评价指标

在本文中对推荐效果的评价主要采用精确度、召回率以及F1 三个值作为指标。

精确度［25］表示预测为正的样本中真正为正样本的数目，其计算式为：

其中：TP表示预测为正，实际也为正的样本数；FP表示预测为正，实际为负的样本数。

召回率［25］表示样本整体中正样本被预测为正的数目，其计算式为：

其中：FN表示预测为负、实际为正的样本数。

F 值［26］是将精确度与召回率综合评价的一个指标，其计算式为：

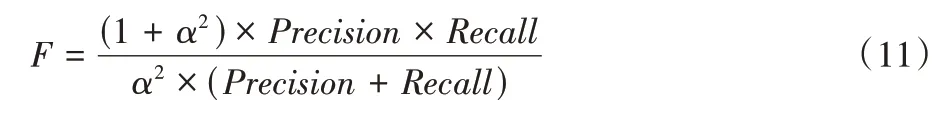
当α=1 时，F 值即为F1 值。

4.3 与GRHC、KNN以及PMF的对比

为验证ACGA 推荐时的有效性，在7 个抽样数据集上与GRHC 算法以及K最近邻（K-Nearest Neighbor，KNN）算法进行了对比。由于ACGA 在初始概念集合上进行一轮遗传运算与多轮遗传迭代得到的近似概念数量不变，后者时间复杂度高，因此本文ACGA 仅进行一轮遗传操作。在抽样数据集上的对比实验结果如表4 所示。

表4 ACGA与GRHC算法以及KNN算法在抽样数据集上的对比Tab.4 Comparison of ACGA，GRHC algorithm and KNN algorithm on sampling datasets

从表4 可以看出，在以上7 个抽样数据集中，ACGA 的召回率在大部分抽样数据集上高于GRHC 以及KNN 算法；在精确度方面，ACGA 在ML-100K 的两个抽样数据集上优于GRHC 以及KNN 算法，在其余几个抽样数据集上持平或略差于GRHC 以及KNN 的效果；在F1 方面，ACGA 基本与GRHC以及KNN 算法持平，甚至优于其余两个算法。因此由遗传算法生成的近似概念在推荐过程中起到了提升推荐效果的作用。

另外，在ML-100K 和ML-1M 的完整数据集上对比了ACGA 与GRHC 算法、KNN（k=3）以及概率矩阵分解（Probabilistic Matrix Factorization，PMF）算法［27-28］的推荐效果，见表5。PMF 算法在矩阵分解算法的基础上融入了概率论相关知识，以概率来预测用户对项目的评分。

如表5 所示，ACGA 在两个数据集上均较GRHC 的推荐效果有一定幅度的提升，证明了近似概念的有效性；对比基线算法，ACGA 精确度高于PMF 以及KNN，分别提升了57%和12%，召回率仅次于KNN，较PMF 提升了104%，F1 值与KNN 基本持平，较PMF 提升了78%。

表5 ACGA与其他算法在完整数据集上的对比Tab.5 Comparison of ACGA and other algorithms on complete datasets

5 结语

本文提出基于遗传算法的近似概念构造算法，并将近似概念用于推荐过程。通过对概念的交叉、选择与变异操作，得到外延相似度高的近似概念，以提高推荐时的准确性。本文提供了一种利用近似概念进行推荐的方案，发挥了近似概念中包含的有价值信息的作用，丰富了概念集合所包含的信息。目前的研究中近似概念生成时的约束条件以及交叉、变异方案还较单一，不利于生成更多的近似概念；另外在近似概念相似度计算时仅利用了评分形式背景，对于属性的类别等信息未加以利用；最后推荐时仅在二值的基础上进行推荐置信度的计算，未利用评分信息。这些问题在今后的研究当中都可继续深入。