基于麻雀搜索优化支持向量机的短期风机发电功率预测

王维高，魏云冰，滕旭东，黄圆

（上海工程技术大学 电子电气工程学院，上海 201620）

0 引言

风力发电已成为全世界应用最为广泛和最为成熟的技术。风电装机规模也愈发庞大，据国家统计局数据显示，2020 年12 月中国风力发电量达到409×10kW·h，同比增长7.1%；2020 年1～12 月中国风力发电量累计产量4.146×10kW·h，累计增长10.5%；2015～2020 年中国发电量逐年递增，2020年达到最高。然而，由于风的随机性和间歇性问题，风力发电并不稳定，给风电并网带来极大的困难，风电功率预测问题日益突出。

短期风电预测模型主要包括物理模型、时间序列模型和人工智能模型3 种。其中，物理模型需要风速、风向、温湿度等气象信息数据，并以此为依据建立复杂的数学模型，该模型在针对短期风电预测时误差较大；时间序列模型需要和历史风电功率数据结合进行建模，在低阶模型中预测精度低，在高阶模型中参数不易确定；人工智能模型是目前最为常用的模型，通过对大量样本学习和训练，建立风电功率与特征量之间的关系，其中支持向量机是目前较为常用的模型，因为支持向量机基于结构风险最小化设计，能够很好的解决过拟合问题，在线性回归方面表现良好，能够防止过度学习，泛化能力好。因此，本文采用支持向量机搭建组合模型。支持向量机在选择学习参数上一般采用交叉验证法，此方法可能会在选择学习参数过程中陷入局部最优，因此一些优化算法也被应用到SVM（Support Vector Machines）预测模型当中，如：文献［6］～［8］采用遗传算法、灰狼算法和粒子群算法对SVM 中的学习参数进行优化选择，以提高精度。但遗传算法、灰狼算法和粒子群算法都面临过早收敛的问题。文献［9］采用BP 神经网络算法预测风电功率；文献［10］采用人工蚁群算法优化神经网络，构建ABCBP（Artifical Bee Colony-BP）神经网络风电功率预测模型，但BP 神经网络算法和蚁群算法收敛速度慢，且有局部极小化问题。

针对上述问题，本文引入麻雀算法优化支持向量机学习参数的选择，提出SSA-SVM（Sparrow Search Algorithm-Support Vector Machines）预测模型。通过与GA-SVM（Genetic Algorithm-Support Vector Machines）和SVR（Support Vector Machines）模型的预测结果对比，验证本文提出的模型在预测精确度上的提升。

1 麻雀搜索优化算法

麻雀搜索算法是受麻雀觅食行为和逃避捕食行为启发而提出的，具有寻优能力强，收敛速度快等优点［11］。

每一只麻雀代表一个位置属性，即其找到食物的位置。在全局中每一只麻雀扮演3个不同角色，发现者，在一定范围内搜索食物；加入者，跟随发现者发现最好的食物；警戒者，警惕周围危险，察觉危险时发出警告。

在维解空间内每只麻雀位置（，，…，x），适应度值f＝f（，，…， x），选用均方误差（Mean Square Error）作为适应度函数，公式（1）：

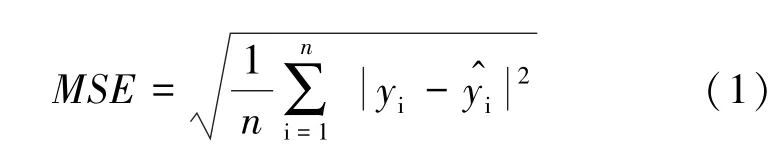
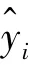
在整个麻雀群体中发现者和加入者数量是不变的，每当增加一个加入者就会减少一个发现者。算法原理：

（1）更新发现者位置，每代发现者位置更新公式（2）：

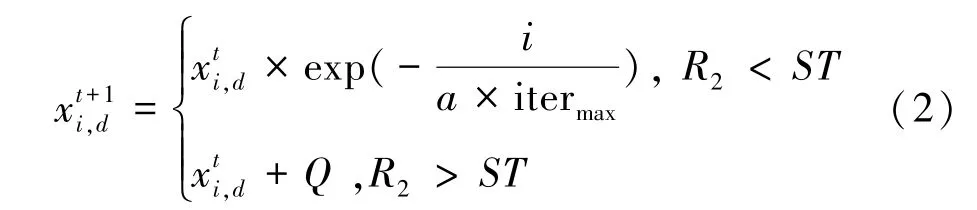
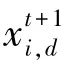
（2）更新加入者位置，加入者位置更新公式（3）：

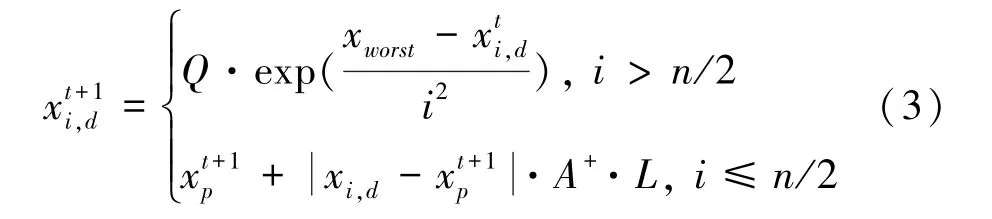
其中，x、x分别表示当前最优位置和最差位置。是1×且每一个元素都被赋值为1 或者1的矩阵，而且A＝A（）。当（05·）时，表明适应度值较低，第个加入者需要飞往别处觅食。

（3）警戒者：在种群中有一部分麻雀在各自觅食过程中会时刻警惕附近危险，一旦发觉附近有危险就放弃食物或者觅食，然后飞往安全区域继续觅食。

每代种群当中都会有个麻雀负责警示。其位置更新公式（4）如下：

其中，是一个符合标准正态分布的随机数；x表示目前全局最优位置； f表示当前麻雀适应度值并且f、f分别表示当前最好和最差适应度值；表示[1，1]的均匀随机数；表示一个较小数，防止分母为0。从公式（4）中可以看出，当f＝f时，表明有麻雀发现危险，就会转移觅食地点，以避免被捕食；当f ＞f时，表明麻雀在整个种群边缘地区捕食，容易受到其他捕食者攻击。

麻雀算法的流程图如图1 所示：

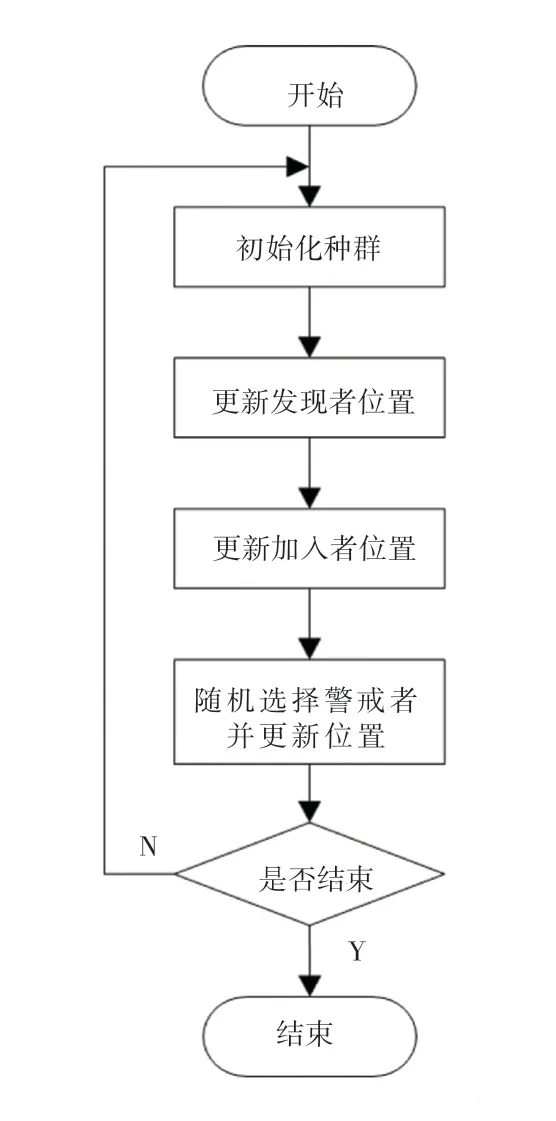
图1 麻雀算法流程图Fig.1 Sparrow Search Algorithm flow chart

2 支持向量机（SVM）原理

支持向量机是一种常用于分类和回归预测的模型，其特点在于能够克服局部最小值，很好的解决过拟合问题，在线性回归方面表现良好，同时能防止过度学习并且泛化能力好。

算法步骤：

（1）选择一个惩罚系数0，构造约束优化问题，式（5）；

为能够将数据映射到高维空间当中，需要用到核函数，本文运用到的核函数是RBF 高斯核函数，公式（6），这样就能将非线性回归问题转化为线性回归问题。

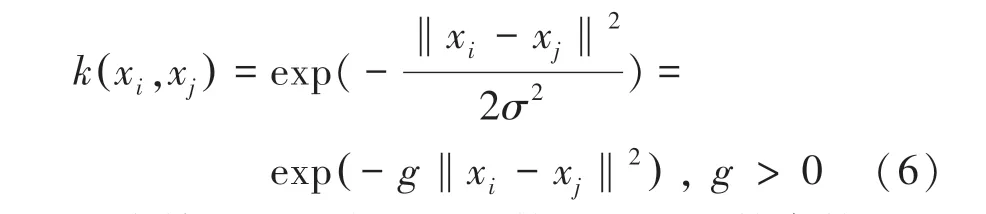
在支持向量机中惩罚系数和核函数参数对整个回归预测精确度产生很重要的影响，所以选择选择合适的参数、就显得尤为重要。本文基于麻雀搜索算法优化参数和，以此优化预测结果。

3 SSA-SVM 预测模型的构建

SVM 基于结构风险最小化设计，能够很好的解决过拟合问题，在线性回归方面表现良好，能够防止过度学习并且泛化能力好。SVM 预测结果受学习参数影响较大，本文基于麻雀搜索算法优化支持向量机的学习参数。

本文采用内蒙古某风电场所测的风速、风向、温度出力作为输入变量，为减少数据的奇异性影响，用公式（7）对数据归一化处理，处理后的数据用于SVM模型的新数据。

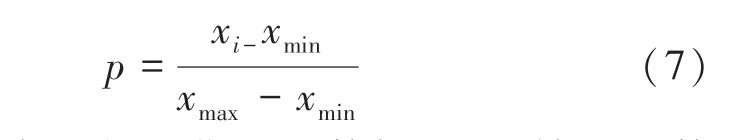
其中：表示归一化后的数据；x原始风速数据；和分别是原始数据中的最小值和最大值。

SSA 参数设置：种群规模20，迭代次数100，参数、范围∈［0001，100］，∈［0，001，1 000］。交叉验证折数5；安全值06；发现者比例07；意识到有危险麻雀的比重02。

麻雀搜索算法会初始一个种群，种群中发现者、加入者和警戒者个体数依照设置参数比例进行分配，根据公式（1）计算麻雀适应度值，并将其作为麻雀搜索到食物的多少；根据公式（2）～（4）更新麻雀的个体位置；根据最佳个体位置确定学习参数，循环100 代结束循环；输出最优参数。

SSA-SVM模型构建具体流程如图2 所示。

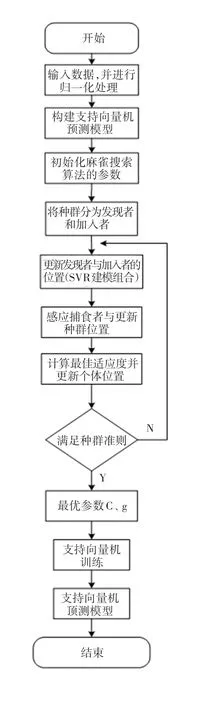
图2 SSA-SVM模型流程图Fig.2 Flow chart of SSA-SVM model

4 仿真分析

以内蒙古某风电场2019～2020 年风场出力数据为例。选取2019／10／01～2020／01／31 数据作为训练集，每隔15 min 一个采样点，共计11 809 组数据；测试集选择2019-11-30～2019-11-31 每15 min一个采样点，共计192个采样点的数据。

为验证SSA-SVM模型精确度的提升，本文搭建SVM、GA-SVM 两种模型进行对比。GA-SVM 参数设置：种群规模20，最大迭代次数20，参数、范围设置∈［0，001，100］，∈［0001，1 000］，交叉验证折数5；个体选择概率09。各模型预测结果如图3 所示，预测误差如图4所示，预测指标见表1。

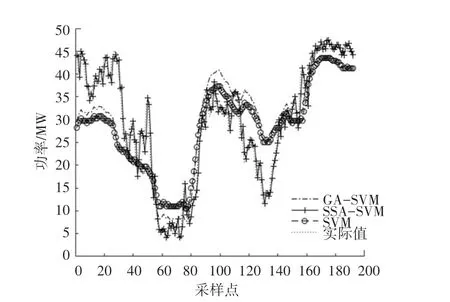
图3 不同算法的预测值对比Fig.3 Comparison of predicted values of different algorithms

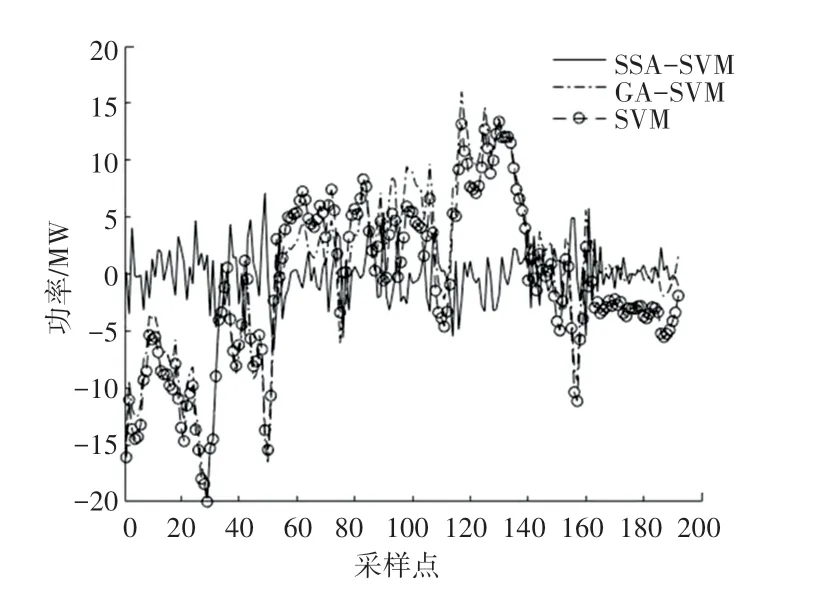
图4 不同优化算法误差对比Fig.4 Comparison of errors of different optimization algorithms

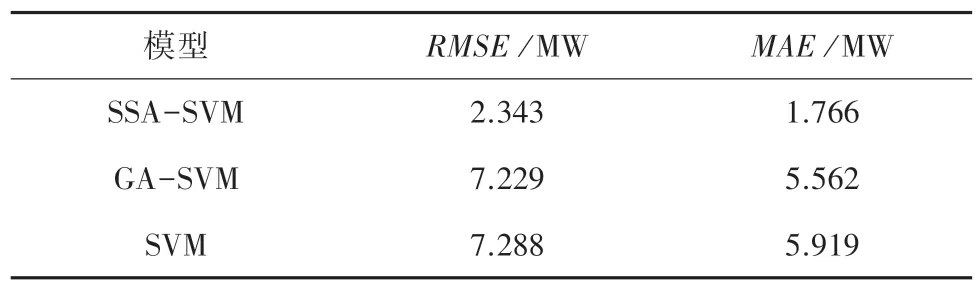
表1 不同模型预测效果对比Tab.1 Comparison of prediction effects of different models

为评价本文所建预测模型性能，引入平均绝对误差（Mean Absolute Eror）和均方根误差（Root Mean Square Eror）作为评价指标。两种评价指标公式（8）和公式（9）：

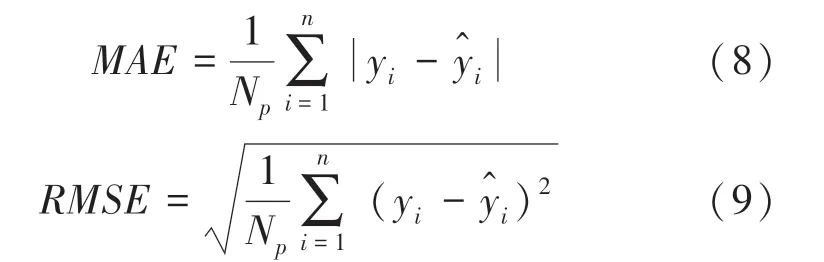
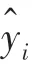
由表1 并结合图3，图4 可以看出：SSA-SVM模型相较GA-SVM和SVM模型，在预测精度上有大幅度提升；较之GA-SVM模型和SVM模型，指标分别减少3.79 6 MW和4.153 MW，相对改善百分比分别为68.25%和70.16%。对比GA-SVM模型和SVM模型指标，SSA-SVM模型分别减少4.886 MW和4.945 MW，相对改善百分比分别为67.59%和67.85%。

综上所述，本文所提出的SSA-SVM 算法在预测精度上改善最佳，GA-SVM 算法次之，SVM 算法最差。验证SSA 算法能有效解决SVM 学习参数选择困难问题，并提高风电预测精确度。

5 结束语

针对提升短期风电功率预测精确度问题，本文提出基于麻雀搜索算法优化支持向量机学习参数，建立SSA-SVM模型，该模型能有效提高支持向量机选择学习参数的效率和预测准确度。在内蒙古某风电场风电预测仿真中，分别与GA-SVM和SVM模型预测结果做对比。

仿真结果表明：在和指标中，SSASVM 预测模型都明显优于GA-SVM和SVM模型，表明SSA-SVM模型适用于短期风电预测。

风电功率序列的随机波动特性导致原始序列中的数据难以被完全挖掘，故需要借助数据分解技术解决此问题，这也是未来重点研究和探索的方向。