基于边界增强和去噪的自适应双权重过采样方法研究

高子寒，宋燕

（上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引言

在机器学习领域，对于不平衡数据的学习是一项极具挑战性的任务。不同类别、不同数量的数据构成的数据集，称为不平衡数据集。如果上述数据集仅包含两个类别，则具有样本数量多的类别称为多数类，其余样本所在类别称为少数类。与此同时，不平衡数据的学习对于研究界也是至关重要的，因为其普遍存在于各种常见的分类任务中。例如，电信欺诈检测、癌症基因检测和推荐系统等等。

传统的机器学习分类器在处理不平衡数据时得到的分类精度通常是不理想的，特别是对少数类的分类效果不佳。这是由于少数类样本的数量太少、所含信息不足，导致分类结果趋向于多数类。但少数类样本中含有的特征往往更重要，因此提高对少数类样本的分类精度是处理不平衡问题的关键所在。通常情况下，不平衡指的是类间不平衡，即两类样本数量的差异程度，而其只是影响不平衡学习的因素之一。影响不平衡的其它因素还包括：类内不平衡、重叠区域的大小和离群点等。

为了更好地解决类别不平衡问题，研究人员提出了两大解决方案，即基于算法和基于数据的解决方案。基于算法的解决方案是通过改变算法的学习方式，增强模型对少数类样本的识别能力，最终降低数据不平衡对分类器带来的消极影响，主要分为代价敏感学习、单类学习和集成学习。而基于数据的解决方案，是通过采样技术改变不同类别的样本数，从而达到多类和少类的相对平衡，其主要包括欠采样和过采样两种方法。与欠采样相比较而言，过采样则充分保留了数据样本所含的重要信息。因此，本文着重于过采样方法的研究。

过采样通常是经过采样或生成合成数据样本来实现的。为了保证合成样本的质量，合成样本应尽可能满足以下要求：不含有干扰信息的噪声且包含有用信息的样本；合成的新样本不能落在多数类区域，以避免类重叠现象的产生。

基于以上基础，本文提出一种新颖的基于边界增强和去噪的自适应双权重过采样方法（ADWEBDO）。该方法通过充分考虑多数类与少数类间的数据分布信息，以及少数类内部的数据分布信息，增加了对边界少数类样本的采样权重，一定程度上避免了类重叠现象的产生；由于利用去噪技术对原始数据进行了去冗余处理，降低了合成噪声样本的可能性；同时基于不同少数类簇的样本特征空间，提出一种基于特征边界组合新样本的策略，不仅保证了合成样本与原样本之间的相似性，而且还增加了合成样本的多样性。

1 相关工作

1.1 模糊C 均值聚类算法

模糊C 均值（FCM）聚类算法是一种基于划分的聚类算法，其基本思想是利用模糊聚类分析方法，将所有对象划分到个簇中，使得划分到同一个簇的对象之间的相似度最大，划分到不同簇的对象之间的相似度最小，以达到聚类的目的。FCM的聚类模型如公式（1）所示：

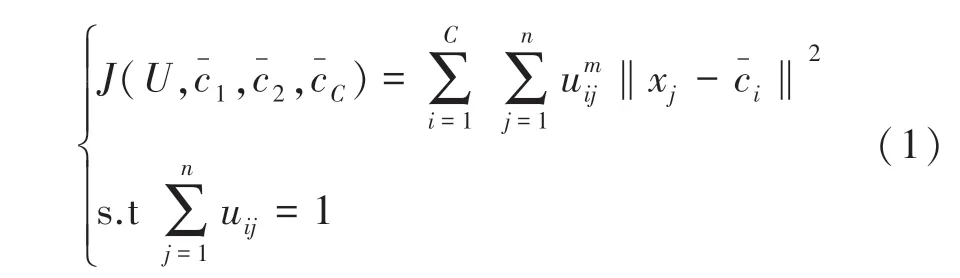
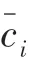
其中，式（2）、（3）中的变量和参数与式（1）中定义的变量和参数相同。

1.2 多层感知机分类算法

多层感知机（MLP）分类算法是一种非线性分类算法，是神经网络的一种。多层感知机的基本结构包括输入层、隐藏层和输出层。不同层之间是全连接的，即上一层的任何一个神经元与下一层的所有神经元都有连接。多层感知机中最基本的单元叫做神经元，图1 表示的是著名的“M-P 神经元模型”。

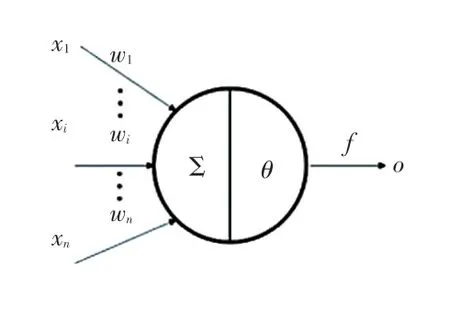
图1 神经元结构Fig.1 Neuron structure

神经元接收来自不同个神经元的输入信号（，，…，x，…，x），这些信号通过个权重（，，…，w，…，w）加权，传递并将总输入值与阈值比较，最后经过激活函数得到输出。神经元的输入和输出关系如公式（4）所示：

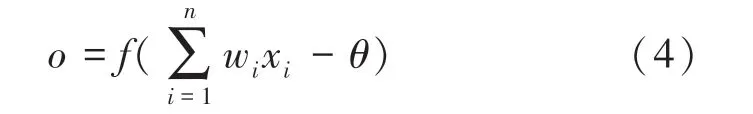
其中，x表示输入的第个神经元； w表示第个神经元的对应的连接权重；表示阈值；（·）表示激活函数；表示神经元的最终输出。

在多层感知机分类算法中，数据首先经过输入层，接着在隐藏层中进行转换，最后在输出层中作出预测。除输入输出层外，中间可以有多个隐层。最简单的多层感知机模型只含一个隐藏层，即3 层结构，如图2 所示。本文将利用MLP 分类器作为后续过采样算法的验证模型。

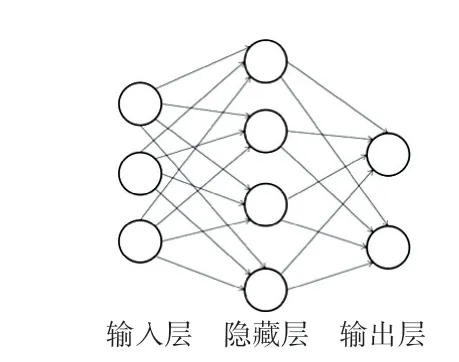
图2 含一层隐藏层的多层感知机模型Fig.2 Multi-layer perceptron model with one hidden layer

2 基于边界增强和去噪的过采样方法

在本文中提出的ADWEBDO 方法，对少数类样本簇使用基于类间距离和簇规模的双指标，自适应为其分配样本合成数，从而增加了对边界少数类样本的采样权重，避免了类重叠现象的产生；同时经过去噪处理，降低了合成噪声样本的可能性；最后基于本文提出的基于特征空间合成样本策略进行过采样，增加了合成样本的多样性。此方法主要包含：去除噪声样本、聚类分析、自适应分配合成样本数、基于特征空间的过采样4 部分。

2.1 去除噪声样本

首先，根据公式（5）计算不同数据集需要新合成的少数类样本的数目。

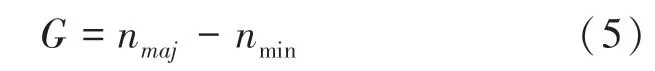
其中，n是原始数据集中多数类样本数，是少数类样本数。

如果选择的目标样本是噪声样本，则新合成的样本也极有可能是噪声样本，最终导致模型性能下降。因此通过去噪可以降低噪声样本生成的可能性。对于原始数据集中的每个少数类样本，通过欧式距离计算其K 近邻。如果此目标样本的所有K近邻都是多数类样本，则将其视为噪声样本并直接将其剔除。同样，对于每个多数类样本执行相同的操作。最后，将剩余的样本添加到集合中，记作过滤后的数据集。

2.2 聚类分析

聚类分析步骤需要为少数类中的不同簇自适应地分配合成样本数。首先，使用FCM 聚类算法，对数据集中的少数类和多数类进行聚类分析，同时获得对应的簇划分结果。少数类划分为个簇，每个簇的聚类中心用a表示，每个簇中包含的少数类样本的数量用n表示；多数类划分为个簇，每个簇的聚类中心用o表示，其中从1 到，从1 到。

2.3 自适应分配合成样本数

为了更好地确定各个少数类簇的合成样本数，充分考虑了簇内数据分布和类间数据分布，提出一种自适应双指标样本分配策略。

第一个指标称为类间距离，即类与类之间的距离越小，多数类和少数类则越接近。为了增加边界少类样本的采样权重，需要增加该少数类簇的权重。类间距离L如式（6）所示。

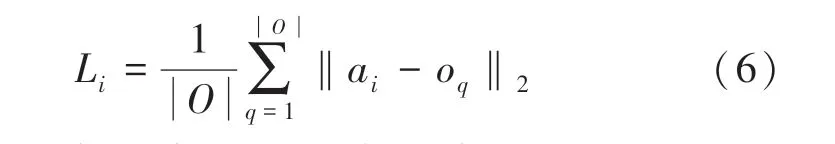
其中，从1 到，从1 到。

当多数类经FCM 聚类之后簇数较多时，不同少数类簇与所有多数类簇的距离之和差距较小。因此，为了增强少数类与多数类的类间距离，通过式（7）将L变换得到R，并对R通过式（8）进行标准化处理。

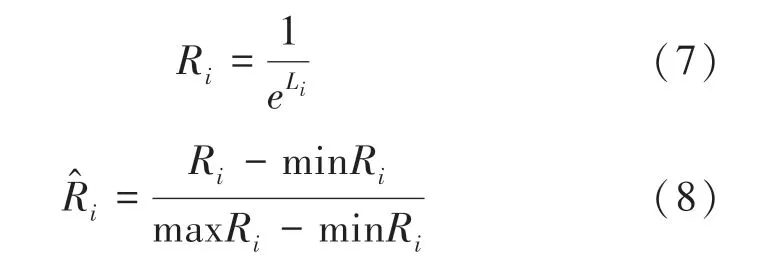
其中，min 表示最小值函数，max 表示最大值函数。

第二个指标称为簇的大小。描述了少数类各簇中所含样本的多少。若该簇所含样本数较多，则过采样时该簇将越应该着重考虑。

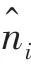
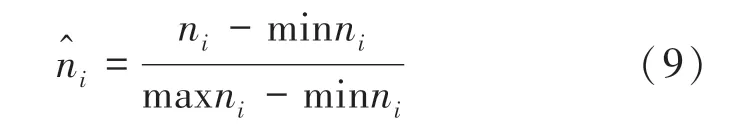
其中，min、max 含义同上。

此外，使用上述两个指标的参数和的加权组合，来构建新的指标F，如式（10）所示。

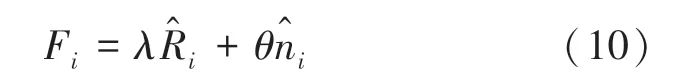
其中，∈［0，1］；∈［0，1］；、表示相应指标的重要性。

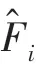
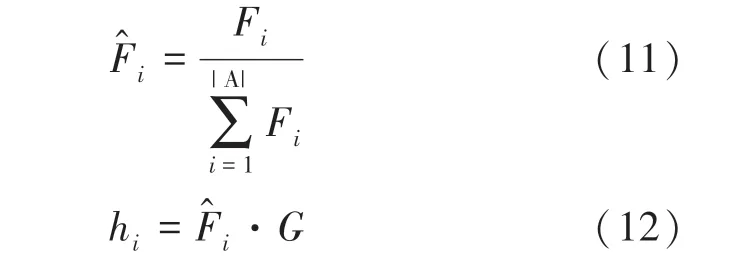
2.4 基于特征空间的过采样

对少数类的每个簇进行过采样，最终在每个簇中分别进行新样本的合成。传统SMOTE的过采样，是通过目标少类样本与其近邻样本的线性插值进行新样本的合成，其合成质量的优劣主要取决于随机因子的大小。该随机因子通常取0～1 之间某个值，若此随机因子取值不当，便直接造成合成样本质量下降，甚至导致合成冗余样本。因此，随机因子的取值至关重要。

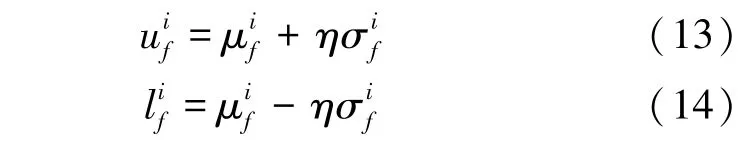
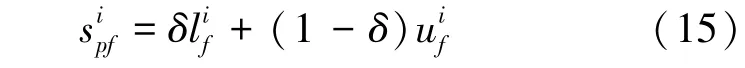
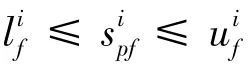
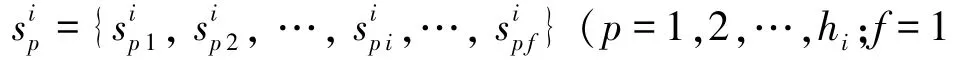
2.5 算法描述

I 为训练集，｛（，），（，），…，（x，y）｝；是训练集样本的总个数，其中少数类样本数为。样本x∈R，是维特征向量，类标签为y∈｛，｝，对应少数类（正样本类），对应多数类（负样本类）。

ADWEBDO 方法的完整步骤如下：

训练集、参数

合成数据集

根据式（5）计算需要合成的新少类样本个数；

对数据集中的所有少数类样本计算其K 近邻，对个近邻均是多数类样本的少数类样本进行剔除，同理对于多数类样本也进行此操作，剔除噪声样本后的数据集记为；

利用FCM 聚类算法，对数据集中的所有少数类样本和多数类样本分别进行聚类分析，根据Xie-Beni 指标，产生个少类簇和个多类簇；

根据双指标，即类间距离和簇的大小，给每个少类簇自适应分配相应数量的合成样本数（利用式（6）～（12）计算得到）；

对每个簇而言，利用式（13）～（15）合成新的少类样本，并重复合成样本的操作，直至满足相应簇需要合成的样本数，并将所有新合成的样本添加至集合中。

3 实验与结果分析

3.1 模型评价指标

本文采用FCM 聚类算法对少数类样本和多数类样本分别进行聚类分析，Xie-Beni（XB）的度量标准是确定FCM 算法需要预先设置的最佳聚类数。此度量标准包含有关每个样本和数据结构的信息。其表达形式如式（16）所示。

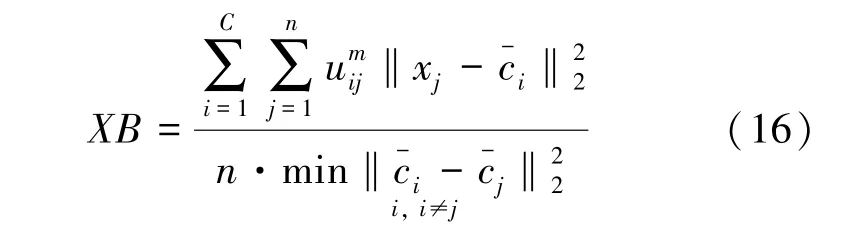
在二元分类问题中，对于不平衡数据的评价方法，大多都建立在混淆矩阵基础之上，见表1。

表1 混淆矩阵Tab.1 Confusion matrix

对于类别不平衡问题，主要关注样本数量少的类是否可以被正确分类。因此，对于不平衡数据的分类，选择准确率（）、精确率（）、召回率（）、1值（1）和曲线下面积（）作为评价指标，其计算方式如式（17）～（20）所示。、、、1和的值越大，意味着预测模型的性能越好。

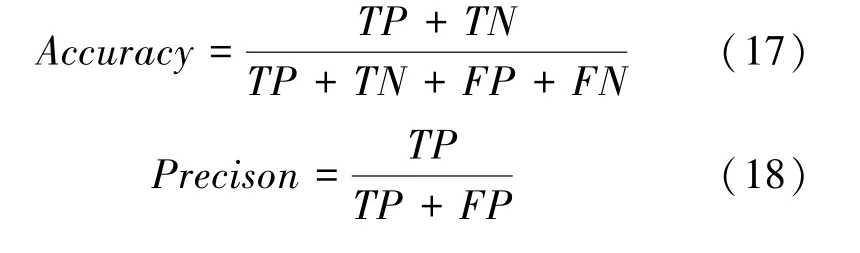
3.2 实验设置

为了研究ADWEBDO 方法的有效性，本文选择来自UCI 数据库的7个不平衡数据集进行实验，数据集信息见表2。

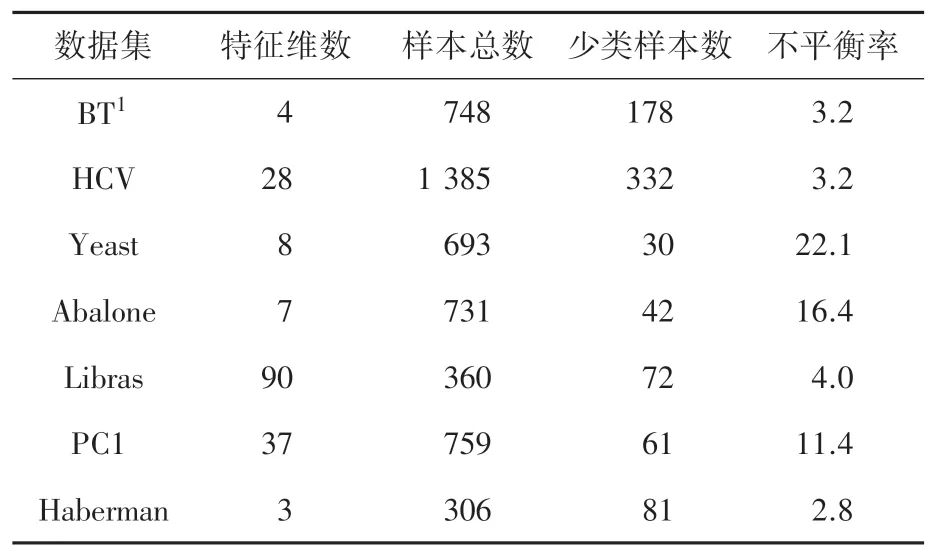
表2 UCI 数据集Tab.2 Datasets from UCI

本文选择多层感知机（Multilayer Perceptron，MLP）作为分类器，MLP的参数均使用默认参数。实验中对比了5 种传统的过采样方法，分别为SMOTE、ADASYN、Borderline-SMOTE1（BS1）、Borderline-SMOTE2（BS2）和CBSO。为了客观比较各个方法，实验将数据集的2／3 作为训练集，1／3 作为测试集，使用十折交叉验证，重复5 次取均值，作为最终实验结果。

所有实验均是在一台Ubuntu 操作系统的电脑上实现，其主要参数为：2.2 GHz CPU、16 GB 内存，同时借助Python 语言编程实现。其它参数选择如下：值的选取参照文献［15］设置为5，FCM 算法中参考文献［19］取2，根据文献［20］，选取2时，实验结果最佳。根据FCM 聚类算法的评价指标，各数据集的最佳少数类簇数和最佳多数类簇数如图3、图4 所示。最佳依次为：09、09、07、05、08、05、08，最佳依次为：01、01、03、05、02、05、02。

图3 7个数据集的多数类的最佳聚类簇数示意图Fig.3 Schematic diagram of the optimal number of clusters for the majority class of seven data sets

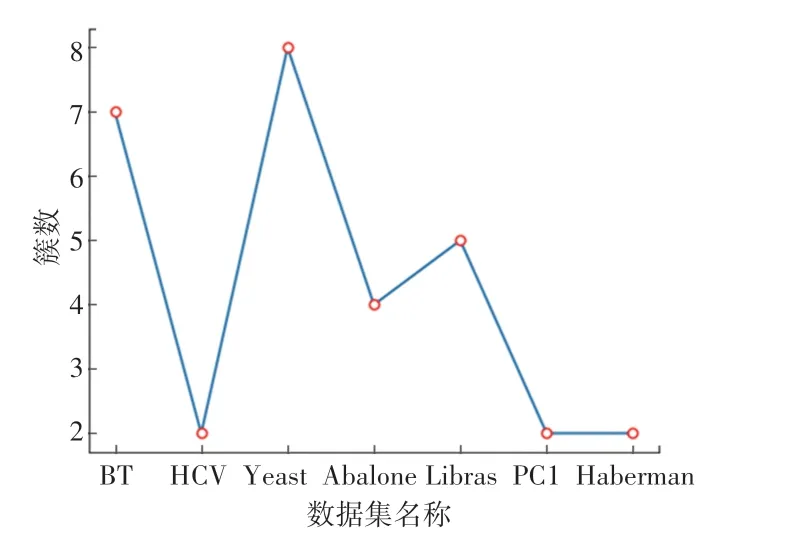
图4 7个数据集的少数类的最佳聚类簇数示意图Fig.4 Schematic diagram of the optimal number of clusters for the minority class of seven data sets

3.3 结果分析

实验结果见表3～表7，其中对最优结果均已进行加粗标注。

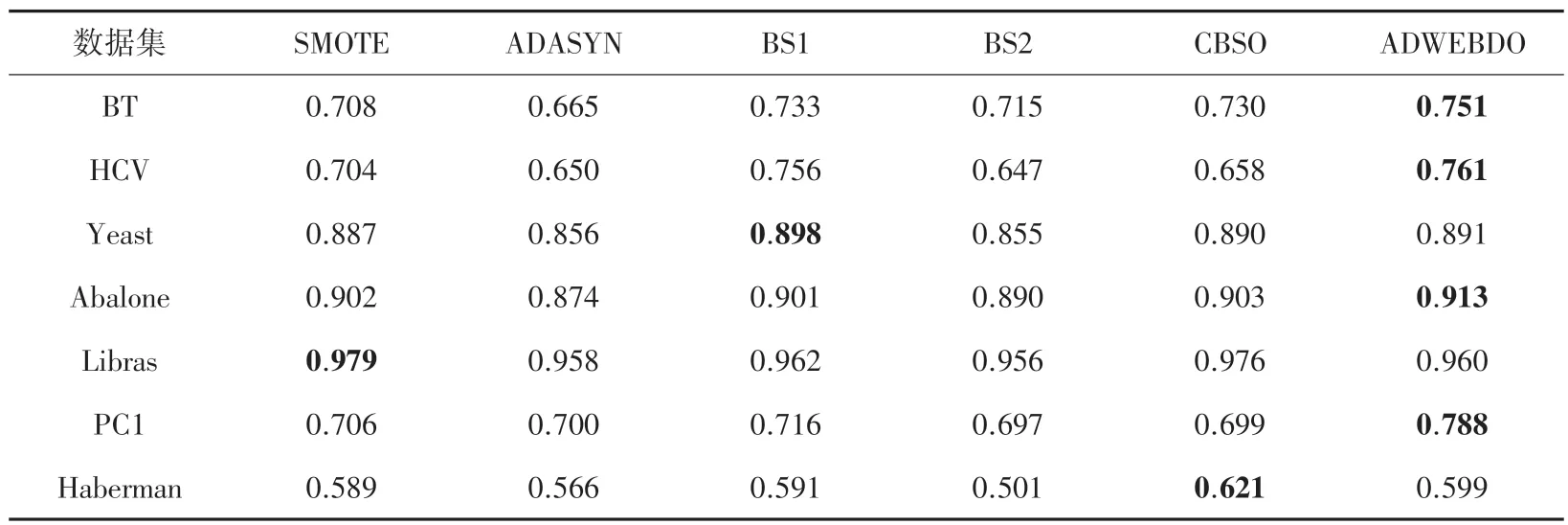
表3 6 种过采样方法在7 组数据集上的Accuracy 结果Tab.3 Results of 6 oversampling methods on Accuracy for 7 datasets

由表3 可见，对于Accuracy 评价指标，本文提出的算法，在BT、HCV、Abalone和PC1 4个数据集上均明显优于其它过采样算法。

表4 中的Precision 指标，ADWEBDO 在5个数据集的表现均优于其它5 种过采样方法。其中，在HCV 数据集上ADWEBDO 比表现较差的ADASYN提高了1.81个百分点。虽然ADWEBDO 在BT和Libras 两个数据集上表现不是最好，但其综合排名为第三，表现良好。

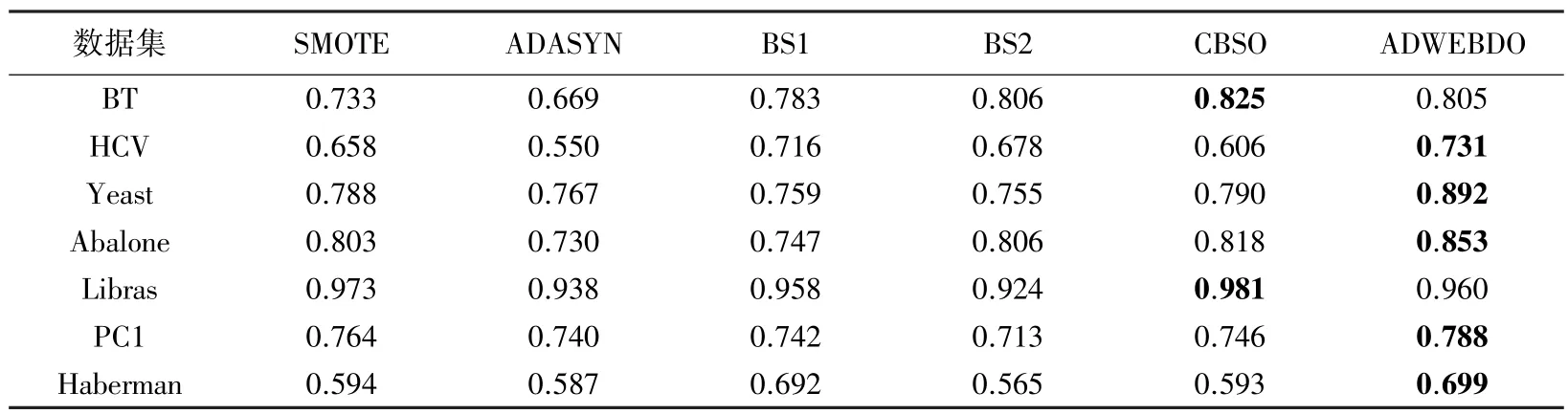
表4 6 种过采样方法在7 组数据集上的Precision 结果Tab.4 Results of 6 oversampling methods on Precision for 7 datasets

Recall的结果见表5。在7个数据集中，本文算法仅在4个数据集上的表现优于其它过采样方法。

表5 6 种过采样方法在7 组数据集上的Recall 结果Tab.5 Results of 6 oversampling methods on Recall for 7 datasets

表6 中的1值，在5个数据集上均优于其它过采样方法。CBSO 在3个数据集上表现良好，其结果仅次于ADWEBDO。

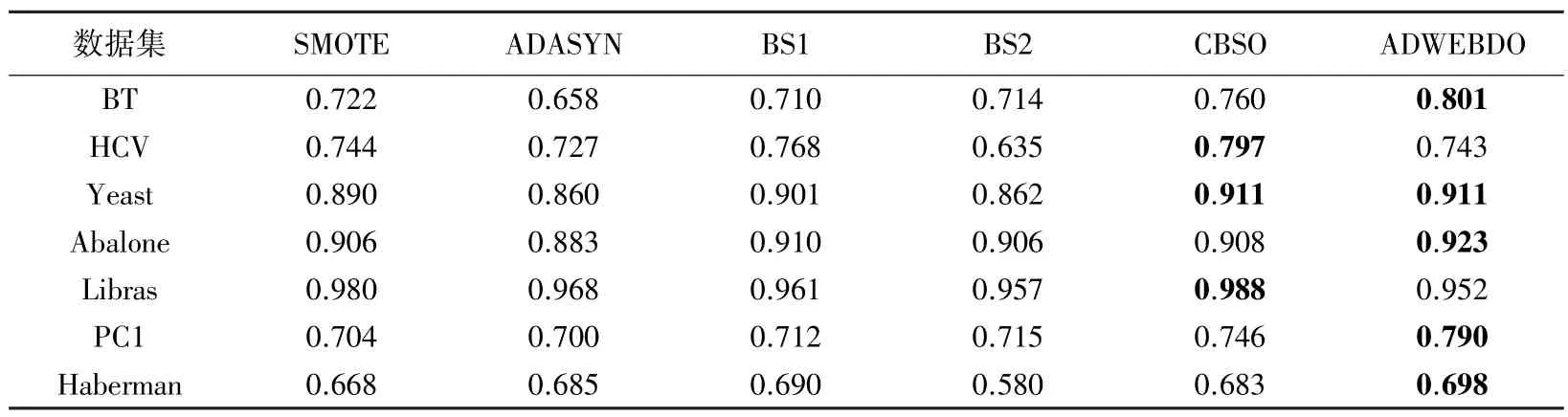
表6 6 种过采样方法在7 组数据集上的F1-score 结果Tab.6 Results of 6 oversampling methods on F1-score for 7 datasets

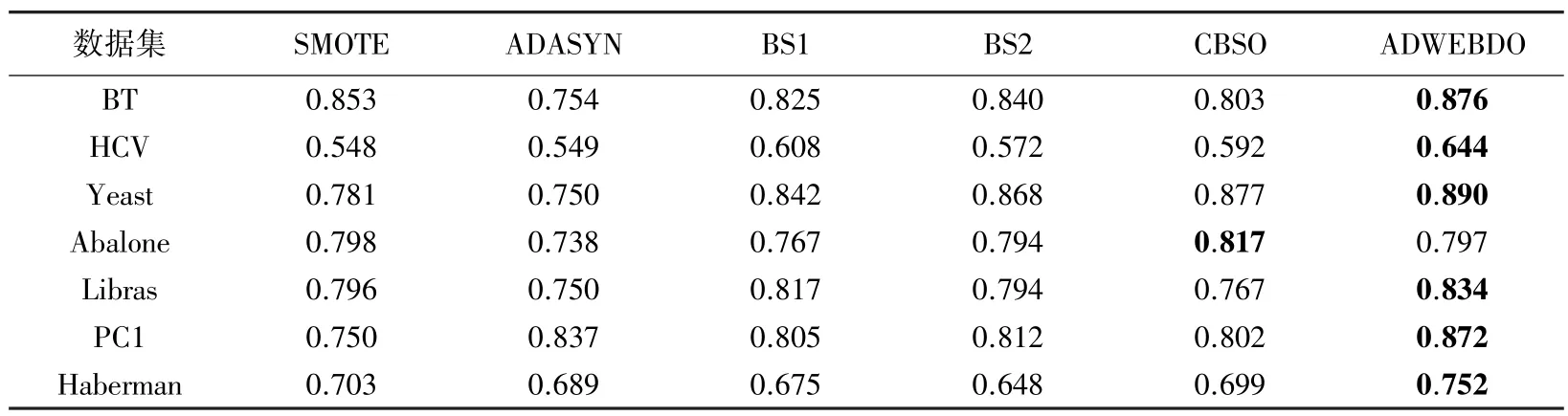
表7 6 种过采样方法在7 组数据集上的AUC 结果Tab.7 Results of 6 oversampling methods on AUC for 7 datasets

AUC 作为不平衡数据分类的重要指标之一，由表7 可知，ADWEBDO 在7个数据集中有6个均是最优结果，这表示ADWEBDO 具有较好的泛化能力。

通过对比6 种过采样方法在7个UCI 数据集上的表现，ADWEBDO 过采样在Accuracy、Precision、Recall、F1-score和AUC 上表现相较于其它5 种过采样方法，均取得了不错的结果。

4 结束语

在不平衡数据的分类问题中，多类样本和少类样本在数量上差距较大，导致分类器的分类性能急剧下降。因此，在实际的分类任务中，必须有效地处理数据不平衡问题。本文提出一种基于边界增强和去噪的自适应双权重过采样方法（ADWEBDO），考虑类间距离的同时，也考虑了少类各样本簇的规模，增加了对边界少类样本的采样权重，一定程度上避免了类重叠现象的产生。同时，基于少类簇特征空间合成新样本策略，使得合成的样本更加合理。实验结果表明，ADWEBDO 在7个不同规模、不同不平衡率的数据集上性能表现稳定，对不平衡数据分类问题的学习具有一定的指导作用。