基于数据挖掘的桥式卸船机抓斗摇摆数值模拟研究

田秀琴

华电曹妃甸重工装备有限公司，河北 唐山 063200

0 引言

桥式卸船机抓斗在卸料的过程中，受到小车加速、减速、抓斗提升以及风力扰动的影响，都会使抓斗出现左右摇摆的情况。当抓斗的摇摆程度剧烈时，则会严重影响到整个桥式卸船机的作业效率。同时，在桥式卸船机抓斗摇摆的过程中，受到力学参数的影响，卸船机的结构载荷会逐渐增加，进而使得加速结构失效，对于生产作业的安全性带来一定负面影响[1]。因此，当前针对桥式卸船机抓斗的控制已经成为了提升卸船机自动化水平和安全水平的主要研究方向[2]。通过建立桥式卸船机抓斗的动力学模型能够实现对动力学特性进行系统化的分析，结合分析结果为卸船机优化策略提供重要依据。当前现有对桥式卸船机抓斗摇摆数值模拟方法都存在没有考虑到与抓斗相连接的钢丝绳及其他结构本身力学特性，没有考虑到装配结构对抓斗摇摆产生的动力学响应影响，无法实现对实际作业中抓斗起升联动的模拟等问题，导致最终获取的数值模拟结果存在一定的缺陷[3]。因此，针对这一问题，为实现对桥式卸船机抓斗摇摆过程中动力学特性更全面的分析，本文在引入数据挖掘技术的基础上，提出一种全新的数值模拟方法，以期为地桥式卸船机抓斗摇摆力学分析提供重要的数据基础。

1 构建桥式卸船机抓斗摇摆过程力学模型

根据卸船机抓斗作业的实际情况，在抓斗摇摆的三个分量当中，只有作用在空间Z轴和空间X轴平面上的分量可以实现对其的有效控制，因此主要针对抓斗驱动机构在空间Z轴和空间X轴平面上构建二维力学模型[4]。图1为桥式卸船机抓斗摇摆过程受力机运动状态示意图。

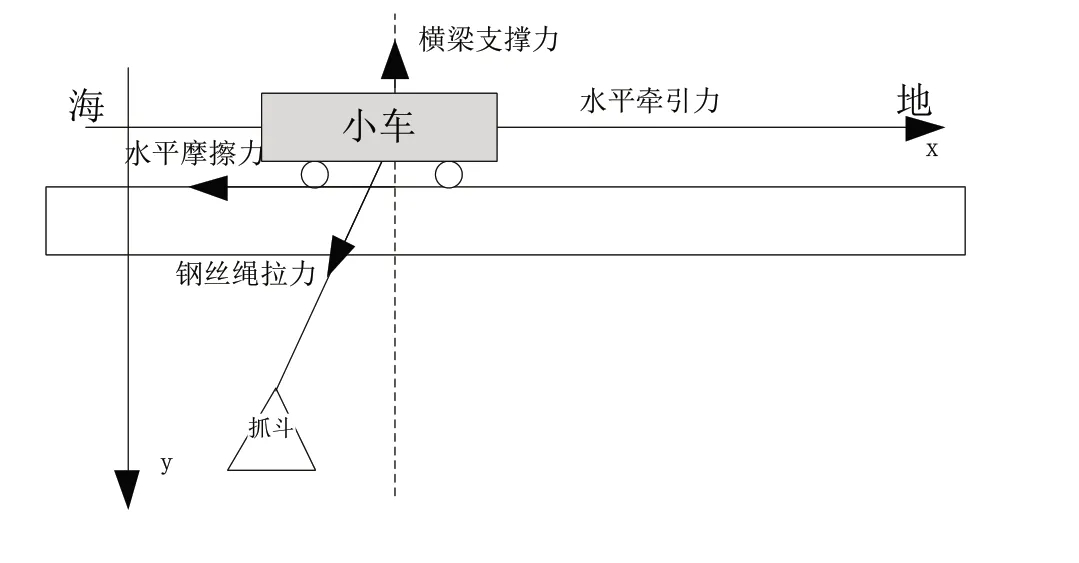
图1 桥式卸船机抓斗摇摆过程受力机运动状态示意图

当抓斗小车在空间Z轴和空间X轴平面运动时，此时抓斗相对于小车而言，在竖直平面上进行摆动运动。在确定这一过程的力学模型时，进行如下假设。

在不考虑抓斗在水平方向和竖直方向进行复合运动的情况下，将小车与抓斗之间连接的钢丝绳长度视为固定不变；将抓斗简化为一个运动的质点，并且只考虑这一质点在空间Z轴和空间X轴平面上的摆动；在建模时，不考虑风力以及空气阻尼以及整个桥式卸船机的弹性变形问题[5]。在此基础上，建立与抓斗连接小车的运动平衡方程进行：

公式中，F表示在抓斗摇摆过程中小车受到来自水平方向上的牵引力；M表示桥式卸船机小车的质量；f表示横梁在水平方向上受到抓斗摇摆运动而产生的水平摩擦力；T表示钢丝绳的拉力；q表示摆动角；表示水平方向上小车的运行速度。同时还存在下述运动平衡关系：

公式中，N表示横梁的支撑力；Mg表示抓斗自身重力。将上述公式（1）和公式（2）结合，并将其作为桥式卸船机抓斗摇摆过程力学模型。

2 基于数据挖掘的抓斗摆角响应求解

在桥式卸船机作业时，与抓斗相连接的小车会按照有规律的变化进行水平方向上的运动，而对应的小车加速度可用下述分段函数表示：

公式中，a表示小车的加速度；s表示设置的加速度数值；t表示加速度计算停止时间；t0表示加速度计算开始时间。在上述基础上，基于数据挖掘技术，通过二阶常系数非齐次微分方程对抓斗摆角响应进行解析求解。在小车加速运行过程中，抓斗的摆角满足加速度段抓斗摆角响应q（t）小于或等于0的条件，此时说明若小车保持一个固定的加速度持续进行均加速运动，则抓斗能够将相对于小车的单摆动运动。当抓斗摆动的运动幅值与小车的加速度成正比，则说明抓斗的摆动运动周期与抓斗连接钢丝绳长度的平均根成正比例关系[6]。在求解的过程中，假设小车的运行时间为20s，加速度为1m/s2，钢丝绳长度为6.5m，则根据下述公式，可计算得出小车运行中加速度段的抓斗摆角响应：

公式中，K表示损失系数。根据上述公式计算，得到小车运行过程中的加速度段抓斗摆角响应。当小车按照固定的加速度运行时，且当加速度逐渐提高并进入下一个匀速运行时，此时可进一步求解出下一个时刻的摆角响应数值[7]。通过对每个时刻摆角响应的分析得出抓斗摇摆产生的作用机理为：当小车作均匀加速时，抓斗与小车作单边摆动；当小车在停车和进入匀速横向移动的时候，既不能满足的条件，那么就不可能同时消除抓斗和小车的位移差异和速度差异，并且在随后的小车匀速行驶段抓斗将保持相对于小车的摆动。

3 设置数值模拟约束条件与作业环境

根据上述论述在完成对抓斗摆角响应的解析与求解，并确定抓斗摇摆产生的机理后，对数值模拟约束条件以及作业环境进行设置。在桥式卸船机抓斗摇摆过程中，需要按照下述两方面内容设置数值模拟的约束条件，以此确保作业时动载荷不会超过设置的抓斗承受能力：一方面，对抓斗的负载进行平衡约束[8]。在抓斗闭合提升时，通过对支撑钢索和开启闭合钢索的载荷分布，保证抓斗在闭合状态下不会受到太大的压力。另一方面，对抓斗的速度进行同步约束。在抓斗开斗上、下移动时，抓斗的开口量是恒定的；当小车前进或后退时，抓斗的高度保持不变。同时，在进行数值模拟前，还需要进行对上述构建的桥式卸船机抓斗摇摆过程力学模型进行简化。不考虑抓斗提升连杆和钢索对抓斗开闭的控制，仅考虑四条钢索对抓斗和小车的连接作用[9]。将驱动装置放置到小车上，并与小车上的一个皮带轮结合，以便在以后的研究过程中减小钢丝绳的整体长度。物理模型中的一些细节几何特性对系统的动态响应没有任何影响，所以在建模时没有将其纳入考虑范围。在完成对桥式卸船机抓斗摇摆过程力学模型的简化后，由于钢丝绳两端的约束条件会对抓斗摇摆运动产生较大的影响，因此需要结合现场装配情况对模型进行反复调试，并确定抓斗与相连接的小车、钢丝绳支架的关系，进而得到下述数值模拟的约束条件。

（1）针对起升钢丝绳两端相连接的第一节圆柱结构，在其与滚筒和抓斗之间均采用球铰约束；

（2）对于开闭钢丝绳两端相连接的第一节圆柱结构，在其与滚筒和抓斗之间均采用轴套力连接约束。对于其他各个部件之间的约束条件设置如下：为了模拟卷筒对钢丝绳的缠绕作用，将每个钢丝绳靠近小车的若干个圆筒与对应的滚筒之间的接触撞击作用力。由于桥式卸船机作业环境位于码头泊位，并且抓斗在高空中作业时，其小车的运行速度较快，因此在数值模拟时将抓斗会受到的空气阻力忽略不计。同时，由于一个移动的物体受到的空气阻力是其速度的平方，根据这一特点，确定空气阻力的计算公式为：

公式中，Fw表示空气阻力；C表示空气阻力系数；A表示抓斗迎风面的面积；r表示空气密度；v表示抓斗在运行过程中的速度。抓斗抓取的材料质量通常比抓斗自身质量要大，而抓斗卸载后载荷质量的改变会对整个系统的动态响应产生一定的影响。为了达到这一目的，利用动态的力来模拟抓取和卸料。在后续进行数值过程中，设置抓斗摇摆的作业环境在.cmd文件当中的代码为：“function=STEP（time，0，0,7.26,3.0E+2）+STEP（time，24.256,0,32.425，-3.0E+5）”。

4 桥式卸船机抓斗摇摆数值模拟

按照抓斗的运动规律，通过对抓斗的升降高度进行设置，对桥式卸船机抓斗摇摆进行数值模拟。为了保证保对抓斗摇摆的模拟准确度，要求在这一过程中，模型当中需要有足够的钢丝绳段数，但此时会造成数值模拟过程中的计算量过大。为了能够解决这一问题，在进行数值模拟的过程中，采用一根钢丝绳对四根钢丝绳进行等效建模，以此实现通过一根钢丝绳对多根钢丝绳的模拟[10]。在模拟过程中，可进一步得出下述等效依据：抓斗的摆动周期与安装机构有关，当缆索长度相同时，四个钢丝绳连接的抓斗摆动周期比单一缆索连接的抓斗摆动周期要大；抓斗摇摆响应对钢丝绳两端约束条件的变化比较敏感；抓斗的摆动反应对于小幅度的振动和自身的刚度和阻尼的变化不太敏感，但对抓斗的摆动反应有明显的影响。根据上述三点，再确定钢丝绳与小车之间的连接关系。通过图2所示的过程，实现对抓斗摇摆角度、抓斗摇摆角度、小车运行速度的数值模拟。

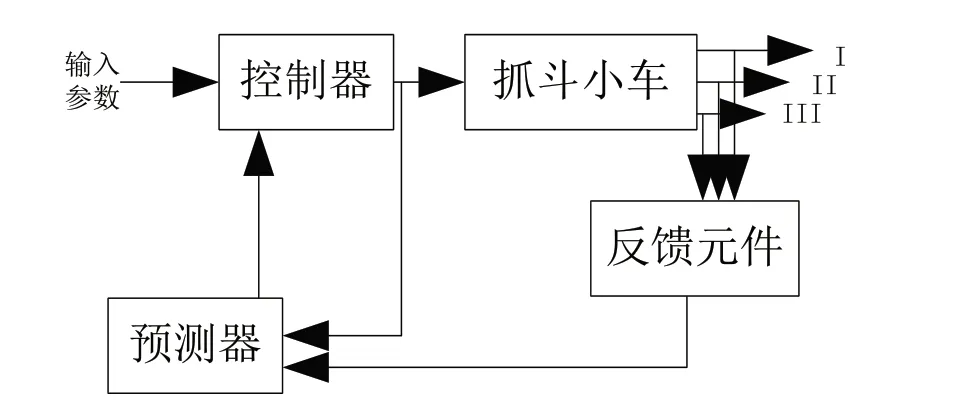
图2 桥式卸船机抓斗摇摆数值模拟

图2中I表示抓斗摇摆角度；II表示抓斗摇摆角速度；III表示小车运行时的速度。图2中预测器的功能是基于该反馈单元的当前状态变量和输入的参数，对小车在目前的加速工况下达到最大转速瞬间的状态变量进行预测，并向控制器输出该预测值。数值模拟过程中控制器作用是基于反馈单元的状态变量当前值和预测器的状态变量预测值，并在满足用户的输入参数的情况下，利用特定的算法对小车的加速度进行调整，以此根据上述论述内容，实现对桥式卸船机抓斗摇摆数值模拟。

5 模拟实例分析

完成对桥式卸船机抓斗摇摆数值模拟方法的设计后，结合某电厂企业在码头作业的条件，将1600t/h规格的桥式卸船机抓斗作为研究对象，利用本文上述提出方法对该桥式卸船机抓斗的摇摆情况进行数值模拟分析。将该规格的桥式卸船机抓斗的尺寸参数和作业船的型号输入，并输入多种抓斗小车运行速度数值和加速度数值，按照卸料作业过程进行摇摆数值模拟。表1为数值模拟输入固定初始参数表。

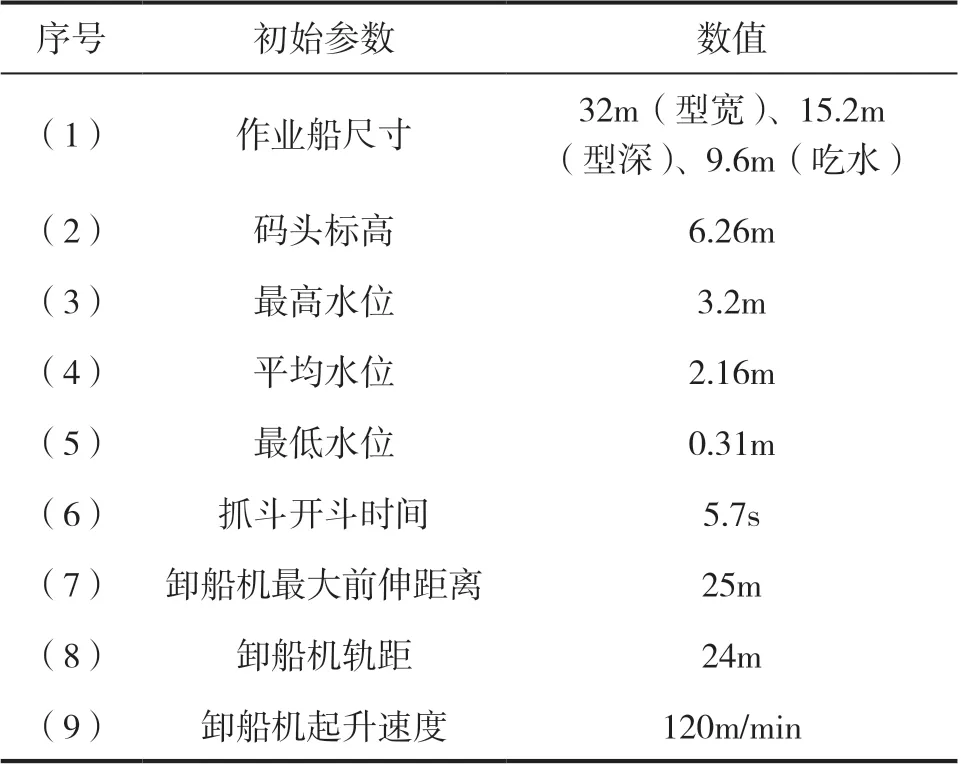
表1 数值模拟输入固定初始参数表

在完成对固定初始参数的设置后，在数值模拟过程中可变参数包括抓斗小车的运行速度，将其速度设置为从120m/min到150m/min，每间隔10m/min设置一个条件，共设置4个抓斗小车运行的条件。将小车运行的加速度也设置为四个不同条件，分别为1.0m/s2、1.1m/s2、1.2m/s2、1.3m/s2。在完成对各项参数的设置后，针对抓斗小车在不同运行速度和不同运行加速度条件下，平均摇摆循环时间、摇摆制动点位置和摇摆折返点位置进行记录，并将数值模拟结果记录成表2。

表2 抓斗小车摇摆数值模拟结果记录表

表2中v表示抓斗小车运行速度；a表示抓斗小车运行加速度。同时，在桥式卸船机抓斗摇摆数值模拟的过程中，针对不同水位，抓斗小车的平均摇摆循环时间也存在一定差异，当处于最高水位时，平均摇摆循环时间为40.26s；当处于平均水位时，平均摇摆循环时间为41.26s；当处于最低水位时，平均摇摆循环时间为42.36s。结合上述选择的1600t/h规格桥式卸船机抓斗以及作业船的参数情况，若采用一般卸船作业方式，则其平均作业时间应当在50.00s以上，而从表2中得到的数值模拟结果可以看出，采用摇摆卸料的作业方式，平均作业时间均明显小于50.00s。因此，通过分析得出，采用摇摆作业方式能够有效提高桥上卸船机的作业效率。通过抓斗运行响应分析进一步得出，抓斗产生摇摆的机理为：当抓斗小车均匀加速时，抓斗与小车作单边摆动；当小车在静止状态下处于均匀的水平移动状态时，抓斗的抓斗角和角速都不能满足变化条件，因此抓斗和小车的位移差异和速度差异就不会被同时消除，而在随后的匀速行驶段，抓斗将会相对于小车的摆动。同时在进行桥式卸船机抓斗摇摆数值模拟过程中发现，通过对具有一定空间装配关系的多根钢丝绳进行建模，数值模拟结果更加全面，能够为桥式卸船机抓斗摇摆动力学分析提供有力支撑。

6 结语

通过本文上述论述，在引入数据挖掘技术的基础上，提出了一种针对桥式卸船机抓斗摇摆情况的数值模拟方法。该方法在数值模拟过程中能够充分考虑装卸料、空气阻力等实际作业时常出现的影响因素，实现对抓斗动力学特征的全面、深入仿真，以此实现桥式卸船机抓斗摇摆数值模拟。通过得到的数值模拟结果能够确定抓斗摇摆的作用机理，为实现对抓斗摇摆更好地控制提供依据。