基于粒子群优化算法和F分布的微震源三步定位方法
庞聪,李查玮*,马武刚,程诚,江勇,廖成旺
(1.中国地震局地震研究所,湖北 武汉 430071;2.地震预警湖北省重点实验室,湖北 武汉 430071;3.运城学院数学与信息技术学院,山西 运城 044000)
0 引 言
微震监测技术在矿山岩体破裂、页岩气勘探、地震预警预报等防灾减灾领域[1-3]发挥着重要作用,而微震源定位精度的提高或算法稳定性的改善是微震监测理论研究的重要方向。
微震源定位算法研究已经有许多显著成果,例如传统微震定位算法Geiger法、线性定位法、单纯形法等,后人又在此基础上结合智能算法、最优化思想等创造出一系列有效的微震定位方法。例如,李邵红等[4]为了消除微震定位中已知参数带来的误差与错误,假定全部检波器参数准确,建立微震定位多目标模型,应用多目标遗传算法(NSGA-Ⅱ)进行二次反演,剔除第一次反演获得的定位异常样本值,第二次反演可以获得较为准确的定位结果;朱权洁等[5]在四四组合法定位结果基础上,利用聚类算法逐步过滤掉异常值,并将聚类中心曲线拐点与异常值离散度作为聚类持续与否的准则;丁恩杰等[6]创新地应用TDOA定位原理确立微震定位数学模型,该方法减少了速度因素带来的误差影响,但是研究内容仅局限于若干监测点布置在单维直线上的情况,代表性不足,且微震源定位目标函数存在主观简化的现象,没有给出相应简化的理由。然后,上述微震定位方法虽然在异常值剔除、微震源定位模型、算法判定准则等方面有一定的改进和探索,但是也存在算法复杂度过高、运算速度过慢、方法通用性差、稳健性不好等问题。
传统微震定位算法的研究主要集中于精度的提高,忽视了安全生产管理、地质活动监测中时间的重要性,以及某些智能算法寻优结果随机性大、稳健性差的现状。对于微震源定位结果的评价,主要依据误差精度、算法执行效率、算法稳定性等方面。陈炳瑞等[7]发展了一种基于相邻点到时差目标方程和粒子群算法的微震源分层定位方法,利用矿山发震现状反复校正定位结果,为了得到准确、可靠的定位结果,计算过程过于复杂;李楠等[8]利用L1范数统计原理建立时间残差公式,将监测数据的中位数作为L1范数统计的最佳估计,解决传统微震源定位方法抗干扰性差、误差较大等问题。
针对微震震源定位研究存在的上述不足,本文尝试发展一种结果稳定、解算较快、精度更高的微震定位方法。在监测点到时数据准确的前提下,建立微震到时差目标函数,为了获得准确初值和算法迭代停止阈值,设计由线性定位法、Geiger法、经过优化后的粒子群算法(Particle Swarm Optimization,PSO)等组成的三步反演方法,并将遗传算法、非线性最小二乘算法、模拟退火算法、标准粒子群算法等作为定位方法参考对象,并讨论PSO随机粒子分布对定位效果的影响。
1 关键技术
1.1 Geiger法与线性法
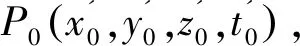
Geiger法具体步骤:先计算每个监测点的走时、震源距离,再计算全体监测点的偏微分矩阵,及时间差值与震源参数残值,最终得到修正后的微震数据。
1.2 粒子群算法
粒子群算法(PSO):它是一种常用的进步型群体智能优化算法,从随机初值Pr(xr,yr,zr,tr)出发,通过更新粒子的飞行方向和飞行速度来寻找最优解,然后通过适应度Fitness(优化目标函数)来评价解的质量,从而获得最优近似解Ppso(x',y',z',t')。
粒子群算法核心是粒子的位置更新公式[7]:
Vid=w·Vid+c1r1(pid-xid)+c2r2(pgd-xid)
(1)
xid=xid+Vid
(2)
式中i=1,2,…,m;d=1,2,…,D;Vid为粒子在第d维的当前速度;w为速度更新惯性权值;学习因子c1和c2为(0,2)区间内的常数;r1和r2为[0,1]范围内的随机数;pid为当前单个粒子目前为止搜索到的最优位置;pgd为当前m个粒子所在粒子群搜索到的最优位置[7]。
1.3 随机粒子对粒子群的影响
在实际矿山开采中,开采环境较复杂,各种人类、机械的非正常活动或微震检波器布置的局限性,都会导致监测系统的随机误差无法遵循正态分布。粒子群算法的随机粒子包含随机位置和随机速度,初值的随机性与分布情况既影响到算法局部搜索与全局搜索的能力,也直接影响算法执行效率。
传统粒子群算法的随机粒子分布情况遵循正态分布、均匀分布,初值的分布情况较为规律和简单,一定程度上增大了定位算法寻优的难度。
(1)正态分布(N(μ,σ2)):该分布在自然界中较为常见,且具备对称性、集中性、曲线面积一定、标准的数学描述方法等明显特征,因而在工程计算中得到广泛应用。粒子群算法随机解常采用标准正态分布(N(0,1)),即每一个随机粒子都服从数学期望为0、方差为1的正态分布。
(2)均匀分布(U(a,b)):包含两个上下限参数a和b,在几何上可看作一个矩形,在概率统计学上描述为相同单位长度上的分布概率相等,其中U(0,1)为标准均匀分布。
(3)F分布(F(m,n)):F分布是由两个独立的卡方分布组合后的分布,其自由度是m和n,实际应用中多采用F(1,1)进行数学运算。
2 基于PSO和Geiger的微震源定位流程
(1)首先,获取微震监测到时数据与微震监测系统监测点坐标,作为算法的原始输入数据。
(2)根据线性定位法原理,建立线性矩阵关系式,随机选取4组监测点数据,计算得到初始反演结果,记为P2。线性法的矩阵关系式具体为:
P∂=β
(3)
(4)
P=(x0,y0,z0,t0)
(5)
(6)
上式中,α为系数列向量,P表示微震求解参数,β为结果矩阵。
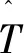
(7)
(5)异常值判断。重复循环执行上述方法n次(可取20或100),获得震源定位近似解集。异常值判定准则为:
(8)
上式中,异常因子λ(λ>0)表示该法最优震源解与Geiger解的各向最大差异阈值,可取为[5,20];Dist(·)表示两点之间的空间距离。异常值判定准则在几何意义上可描述为一个以为球心、除去球面的圆球状几何图形,超出此范围的点被视为异常值,予以去除,异常值数目记为ρ。
(6)对n-ρ个有效震源近似解按照质心法求解最终微震源结果。
3 工程验证
3.1 微震数据描述
为了验证本文提出的定位方法的有效性和进步性,应用吕进国等[9]公开的某开采矿井工程实验数据进行验证。该矿一共安装了30个微震监测单元,爆破位置为[8 732.70,6 570.60,511.30]及起爆时刻为10时27分,P波传播速度均值为5 700 m/s,爆破成功后观测到8个P波到时数据,分别记为T1~T8,如图1所示,实验仿真阶段采用MATLAB 2019A数据处理工具以及相应的标准函数工具箱。
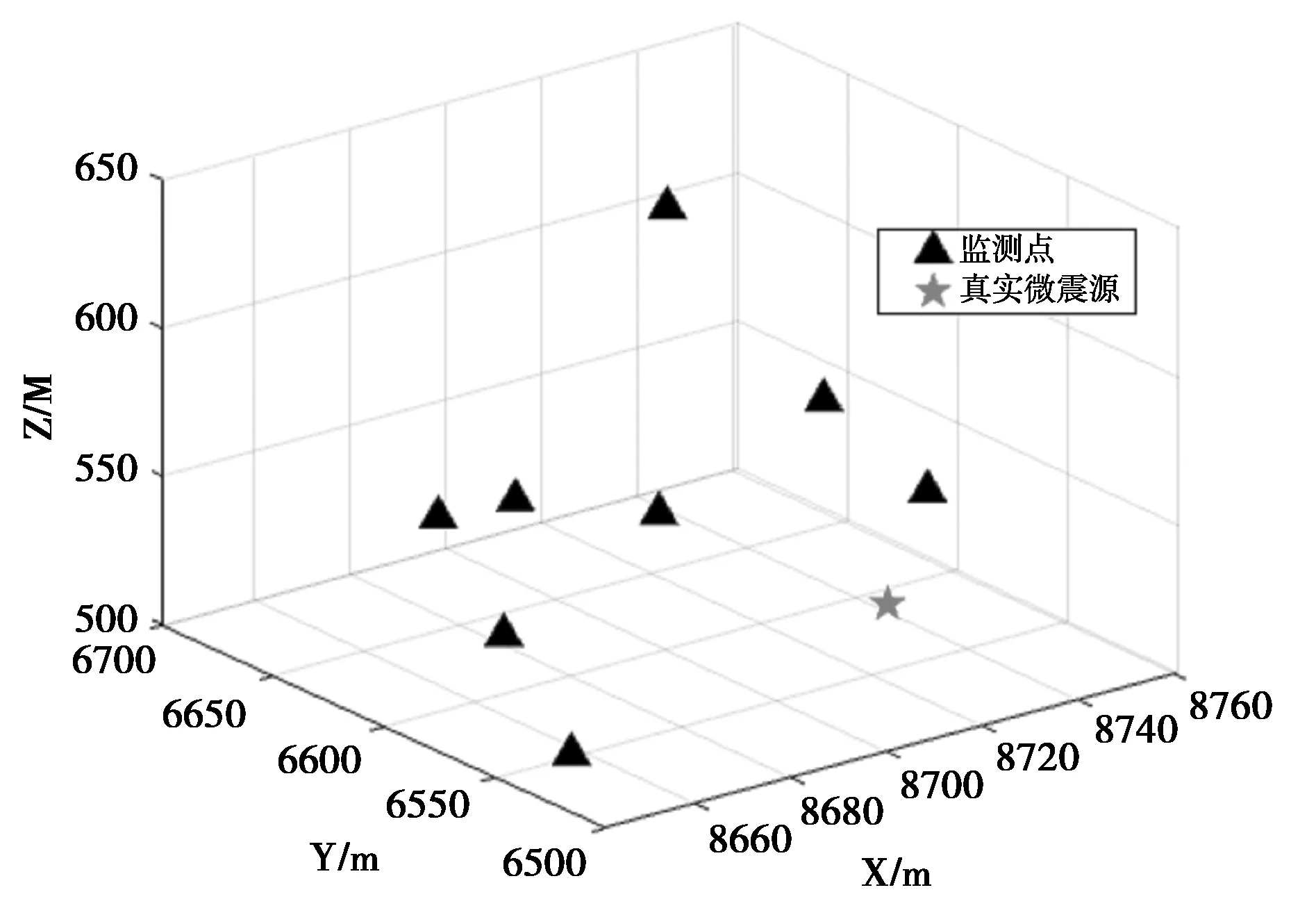
图1 微震监测点位置
算法中PSO的具体参数为:粒子数目N为50,学习因子为1.5,学习因子为2.5,惯性权重为0.5,最大迭代次数D为100。
3.2 粒子群随机粒子对定位的影响
为寻找适合本算法和微震定位模型的随机分布,在STD循环判定准则、到时差模型、循环重复100次等条件下,测试正态分布、F分布、均匀分布等不同随机对象对算法定位结果的影响,分布参数同第一章节所述。
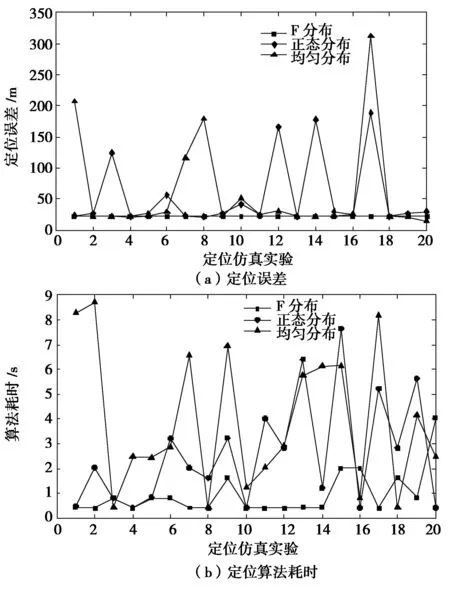
图2 随机粒子服从不同分布下的定位结果
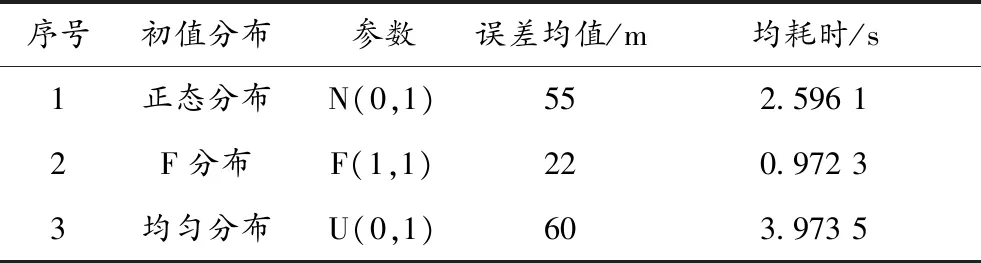
表1 随机粒子服从不同分布下的定位结果统计
从图2和表1可看出,F分布的定位精度及寻优速度皆优于其他两种分布,均计算耗时达到0.972 3 s,定位误差均值为22 m,而基于均匀分布和正态分布的微震源定位效果图都出现了较多的突跳现象,定位性能极不稳定,不利于在实际矿山微震活动监测或页岩气勘探中应用。
3.3 算法对比研究
为了进一步验证三步反演法的优越性,分别取模拟退火算法、粒子群优化算法、遗传算法、非线性最小二乘算法等方法对微震活动监测数据进行震源反演,不同经典算法与本文方法的性能对比结果如表2和图3所示。
由表2和图3可知,非线性最小二乘法虽然定位性能稳定,但是震源求解精度不高,标准粒子群优化算法受制于部分超参数设置困难,定位结果误差极大,体现了PSO易陷入局部最优的显著特点,而本文方法吸取了Geiger法、群体智能优化算法等方法的优势与不足,加入了异常值提出步骤,反演结果误差较小,定位性能显著稳健。
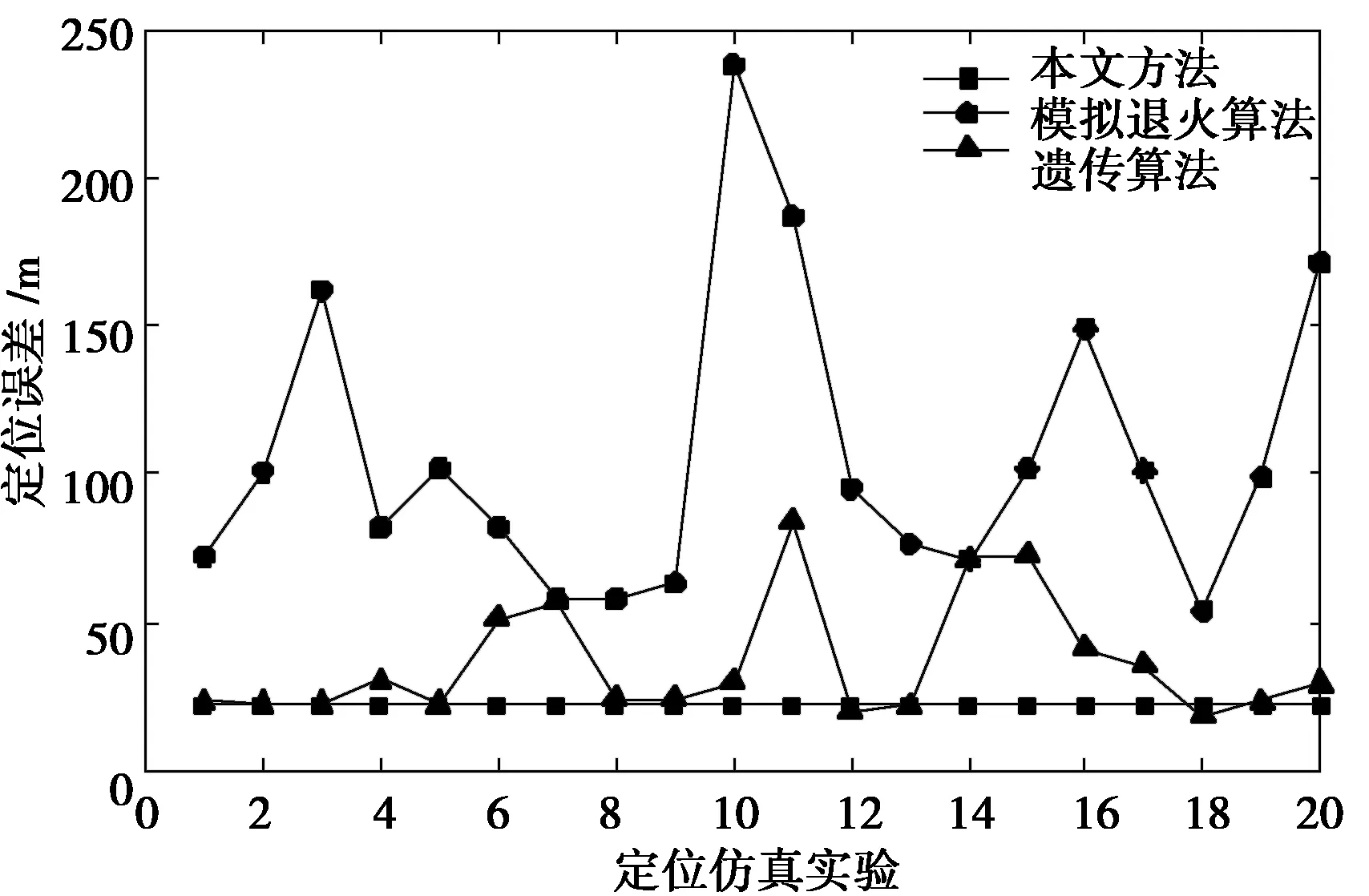
图3 微震源定位方法对比

表2 微震源定位方法对比结果
4 结 论
(1)本文设计了三步微震源反演方法,通过结合线性定位法、Geiger法、PSO等算法的优劣势,将线性定位结果作为Geiger法的初值,较好地解决了Geiger法受初值影响较大的情况;将Geiger法定位结果作为下一步的循环判定准则,解决了粒子群算法在微震定位求解时最优解随机性大、误差较高、稳健性差的问题。该算法结构清晰、稳定性好,误差相对PSO、GA、SA等更小。
(2)对粒子群算法进行改进,通过随机初解分布寻优,较全面的对比了正态分布、均匀分布、F分布等随机分布对算法定位精度与效率的影响,找出合适的随机分布匹配PSO算法的随机粒子。合理选择随机分布,对获得较为准确、高效的定位算法结果有重要意义。
鉴于研究时间有限,并未对正态分布、均匀分布、F分布等分布的分布参数与微震定位的关联做更为详细的剖析;可以从各类随机分布规律出发,独立设计一种随机分布选择函数或混合分布函数,适应不同地质条件、不同数据质量下微震定位算法,以达到算法质量的自动优化。

