混合运输机场跑道服务能力评估模型

康瑞， 邓皓， 杨凯

(1.中国民用航空飞行学院空中交通管理学院， 广汉 618307； 2. 四川大学视觉合成图形图像技术国防重点学科实验室， 成都 610064； 3.四川大学计算机学院， 成都 610064)

混合运输机场的运行中，运输航班与训练飞行同处一片空域，两种飞行类型对机场关键资源的竞争已成为制约运行安全和效率的主要因素。为保障训练飞行顺利开展、运输航班稳步攀升，分析运输与训练飞行相互影响，量化混合运行下跑道服务能力，是提高混合运输机场运行效率的有效手段。

跑道服务能力由单位时间跑道容量定义。关于跑道容量的研究，国外开始较早，1948年Bowen等[1]基于泊松流模型提出了跑道容量评估模型。随后众多学者在此基础上将管制间隔要求、机型比例、导航设备与人的因素等考虑进模型中[2-5]。国内起步则相对较晚，胡明华等[6]考虑机队混杂、跑道使用规则等，系统建立了跑道容量评估模型；潘卫军等[7]基于数值计算模型进行了单跑道起飞间隔安全分析；康瑞等[8]考虑脱离道构型建立了机场容量评估模型；随着民航业的快速发展，国内机场进入了多跑道时代，学者们考虑机场跑道运行模式与构型等建立了针对性的跑道容量评估模型[9-11]，并不断缩小尾流影响下的航空器飞行间隔[12-14]；与此同时，训练飞行的需求也随之激增，骆菁菁[15]基于目视本场训练和仪表转场训练着陆时间间隔构建了训练机场跑道容量评估模型；康瑞等[16]细化航空器起降滑跑时间构建民航支线机场容量评估模型；陈奇奇等[17]兼顾军用飞机的使用，对民用机场快速滑行道最优位置进行了系统研究。

目前学者对跑道容量的研究取得了丰富的成果，现有跑道容量评估模型仅能量化运输飞行或训练飞行的单一类型的跑道容量，忽略了两种模式混合运行的情况；训练飞行多使用轻型机，运行规则与航空器性能相较于运输飞行存在较大差异，当运输和训练混合运行时，跑道占用时间的差异导致不能将已有模型进行简单叠加，需要针对混合运行的特点进行抽象。

现根据混合运输机场实际情况，设立运输飞行比例参数ra与训练飞行比例参数rb，加入起飞、全停与触底拉升3种飞行训练科目，并综合运输与训练飞行的运行特点和机型差异，分类细化航空器运行过程。参考航空器性能引入进场速度、转弯速度等运行参数，将不同运行阶段的跑道占用时间进行量化，由此构造混合运输机场跑道容量评估模型。

1 混合运输机场跑道运行方式

1.1 运输飞行运行过程

降落如图1(a)所示。可以看出，航空器由进场

速度进港，接地时减速至接地速度；接地后继续减速，跑道冲程结束减速至滑行速度，滑行至最近可使用的脱离道口；接近脱离道口时速度减至转弯速度，通过停止等待线后降落过程结束并允许后续航空器使用跑道。

起飞如图1(b)所示。可以看出，航空器从停机位滑行至停止等待线处等待管制员指令，当得到进入跑道指令后进入跑道并对正，此时速度为航空器转弯速度；航空器得到起飞指令后从静止加速至抬前轮速度vr离地；航空器按照适宜的爬升速度爬升至跑道末端后起飞过程结束，后续航空器得以继续使用跑道。

1.2 训练飞行运行过程

触地拉升科目如图2(a)所示。可以看出，航空器降落接地后速度调整至抬前轮速度vr后拉升起飞；降落全停时如图2(b)所示，为缩短航空器跑道占用时间，可由滑行道A3提前脱离跑道；起飞时如图2(c)所示，训练飞行多采用减跑道起飞的方式，从滑行道A2上跑道对正起飞。

2 考虑混合运输飞行的跑道服务时间计算模型

2.1 模型相关参数

2.1.1 跑道参数

L为跑道长度；LV为脱离道口与跑道头的距离；LH为跑道外等待点与跑道中线的距离；LR为着陆接地滑跑减速至滑行速度的距离。

2.1.2 航空器参数

vh为进场速度，即航空器即将着陆前在安全高度处的瞬时速度；vd为航空器接地时的瞬时速度；vmax为航空器最大滑行速度；vav为平均滑行速度；vt为转弯速度；vr为抬前轮速度；vs为起飞至安全高度瞬时速度；φ为发动机推力作用线与飞机迎角α之间的夹角；μ为跑道道面摩擦因数；Q为航空器所受阻力；P为航空器发动机推力；W为飞机总质量；Rθ为转弯弧长；k为阶段瞬间飞机的升阻比；a为着陆减速度；σS为机翼面积；ρ为空气密度；Cx为水平方向升力系数；Cy为垂直方向升力系数；g为重力加速度。

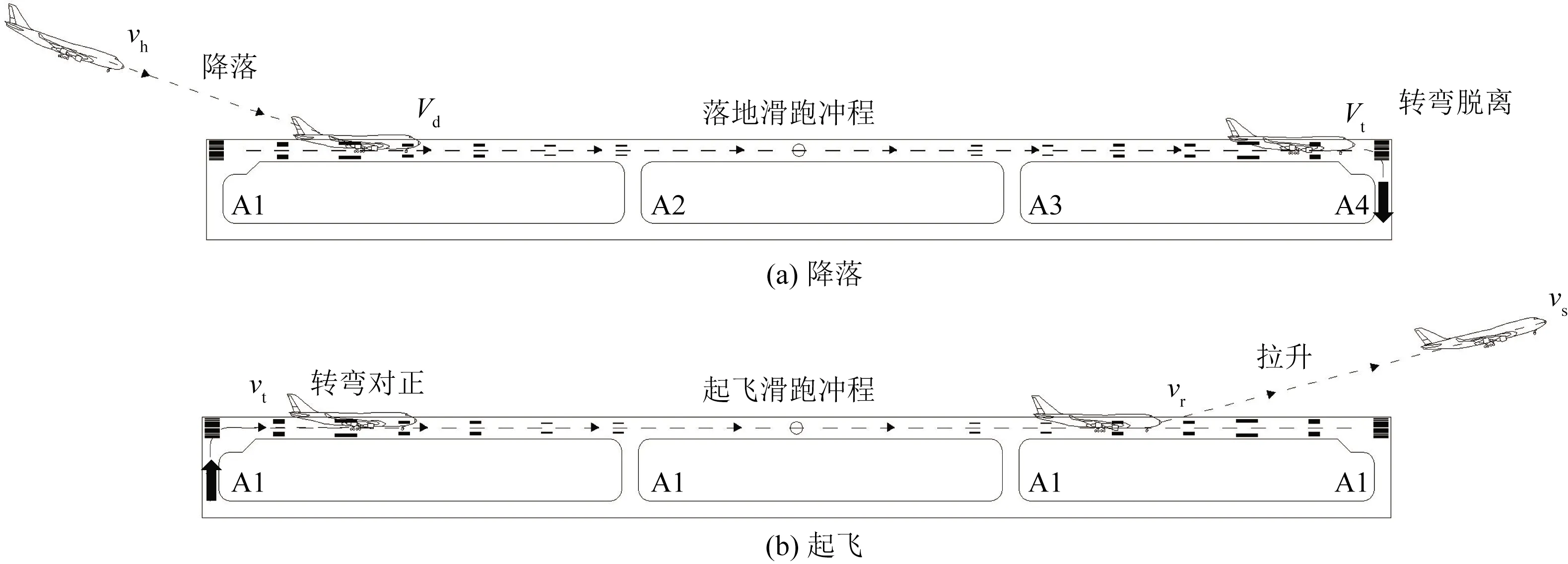
图1 运输航空器起 降示意图Fig.1 Transport flights Landing and Take off sketch map

图2 训练科目示意图Fig.2 Training project sketch map

2.2 模型构造

2.2.1 着陆航空器

滑跑减速至滑行速度的距离[18]为

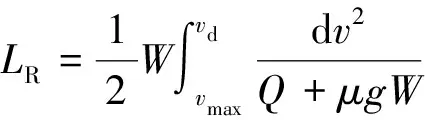
(1)

滑跑减速至滑行速度的时间为

(2)

滑行减速至转弯速度的距离为

(3)

转弯时间为

(4)

滑行减速至转弯速度的时间为

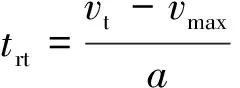
(5)

滑行减速至转弯速度的距离为

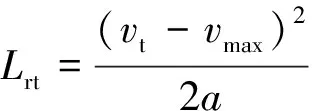
(6)

降落航空器无需180°掉头直接经由滑行道脱离，则跑道占用时间为

(7)

2.2.2 起飞航空器

起飞航空器滑跑距离为

(8)

航空器起飞滑跑及爬升时间为

(9)

起飞航空器进入跑道对准后直接起飞，则占用跑道时间为

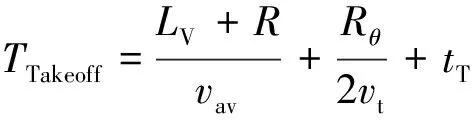
(10)

2.2.3 训练飞行触地拉升航空器

航空器进行触地拉升科目时，进场着陆阶段占用跑道时间与正常着陆航空器占用跑道时间相同，随后加速拉升阶段跑道占用时间分以下3种情况。

(1)若拉升抬前轮时所需速度大于接地瞬间的速度需要加速再抬前轮，即vr>vd时，加速拉升阶段时间tacc为

(11)

(2)若vr≤vd，拉升阶段tgo为

(12)

(3)触地拉升跑道占用时间为

(13)

2.2.4 运行规则

当管制间隔大于降落航空器和起飞航空器跑道占用时间，着陆安全间隔TA和起飞安全间隔TD以管制间隔为实际安全间隔。

TA=max(TATC，Tland)

(14)

TD=max(TATC，TTakeoff)

(15)

当前方航空器完成起飞、触地拉升上升至安全高度后，后方航空器方可占用跑道[19]；当前方航空器完成着陆且脱跑道后，后方航空器方可占用跑道，即同一时间只能有一架航空器出现在跑道上。

2.2.5 跑道运行能力计算

设单位时间T内，起飞、降落航空器比例总和为1，比例分别为rD、rA；其中rA由运输航空器比例ra和训练航空器比例rb组成，而rb则由全停航空器比例rf和触地拉升航空器比例rt组成。

rA=ra+rb

(16)

rb=rf+rt

(17)

rD+rA=1

(18)

单位时间跑道运行能力P为

(19)

3 仿真建模与分析

3.1 Anylogic模型建立

Anylogic是在Java仿真平台运行仿真模型的仿真软件，不仅是第一个将UML语言加入仿真领域的工具，还是对离散、多智能体、系统动力学和混合系统建模仿真的工具。应用非常广泛，包括机场仿真、行人交通、物流、行人疏散、Petri网等[20]。该软件采用模块化建模的方式，可以快速建立一个动态的复杂交互式模型，将实际运行情况合理、准确且真实的反映在模型当中。模型建立流程图如图3所示。

图3 仿真模型建立流程图Fig.3 Simulation modelling flow chart

以某机场为例建立仿真模型，跑道长2 500 m，共有4条滑行道，分别为A1、A2、A3和A4，分别距离西端跑道头0、900、1 600和2 500 m。

图4为Anylogic仿真模型控制模块。其中图4(a)为航空器的生成、起飞和降落比例控制模块，生成智能体后通过条件设置完成降落、起飞航空器的比例控制；图4(b)为不同类型航空器对滑行路线的选择，速度控制则由相应移动组块中的速度控制代码实现。

如图5所示，跑道自左向右运行，图中3号航空器正占用跑道起飞，其余航空器均位于跑道外侧；起飞航空器可根据飞行种类选择相应滑行道，1号航空器为运输飞机，正在滑向并且预计使用A1滑行道进入跑道起飞；2号航空器为训练飞机，在A2滑行道等待点等待，满足间隔等要求后方可进入跑道起飞，使用减跑道起飞缩短跑道占用时间。降落航空器也可根据实际情况选择A3或A4滑行道脱离跑道，4号航空器为运输飞机，降落冲程较长使用A4滑行道脱离，训练飞机则可使用A3滑行道提前脱离跑道。

3.2 数据分析

3.2.1 参数设置

由于混合运输机场存在运输与训练两种飞行类型，故将航空器分为运输飞机和训练飞机，其中运输飞机以中型机为例，训练飞机以轻型机为例。计算起飞、降落、触地拉升各阶段的时间，并量化单位时间的跑道容量，根据不同类型航空器的飞行性能，设置如下参数。

(1)训练飞机。vt=26 km/h，vmax=52 km/h，r=15 m，vr=102 km/h，vs=140 km/h，W=900 kg，vh=120 km/h，vd=93 km/h，k=6.95，LV=1 600 m，LH=60 m，μ=0.3，ataxi=0.2 m/s2。

(2)运输飞机。vt=20 km/h，vmax=55 km/h，r=30 m，vr=278 km/h，vs=315 km/h，W=2 900 kg，vh=260 km/h，vd=240 km/h，k=5.75，LV=2 500 m，LH=60 m，μ=0.3，ataxi=0.25 m/s2。

改变rD、rA、rb、rf的值，每组仿真实验固定两个变量，每次仿真运行8 h取平均数值。得到随飞机起降比例、训练科目比例、飞行种类比例变化的跑道服务能力变化折线图。

3.2.2 训练航空器比例和全停航空器比例对跑道服务能力的影响

设rD=0.3，rA=0.7，rb∈(0，1)，ra∈(0，1-rb)，rf∈(0，1)，rt∈(0，1-rf)，图6为航空器起降比例固定，单位时间跑道服务能力P受rb和rf影响的变化趋势。

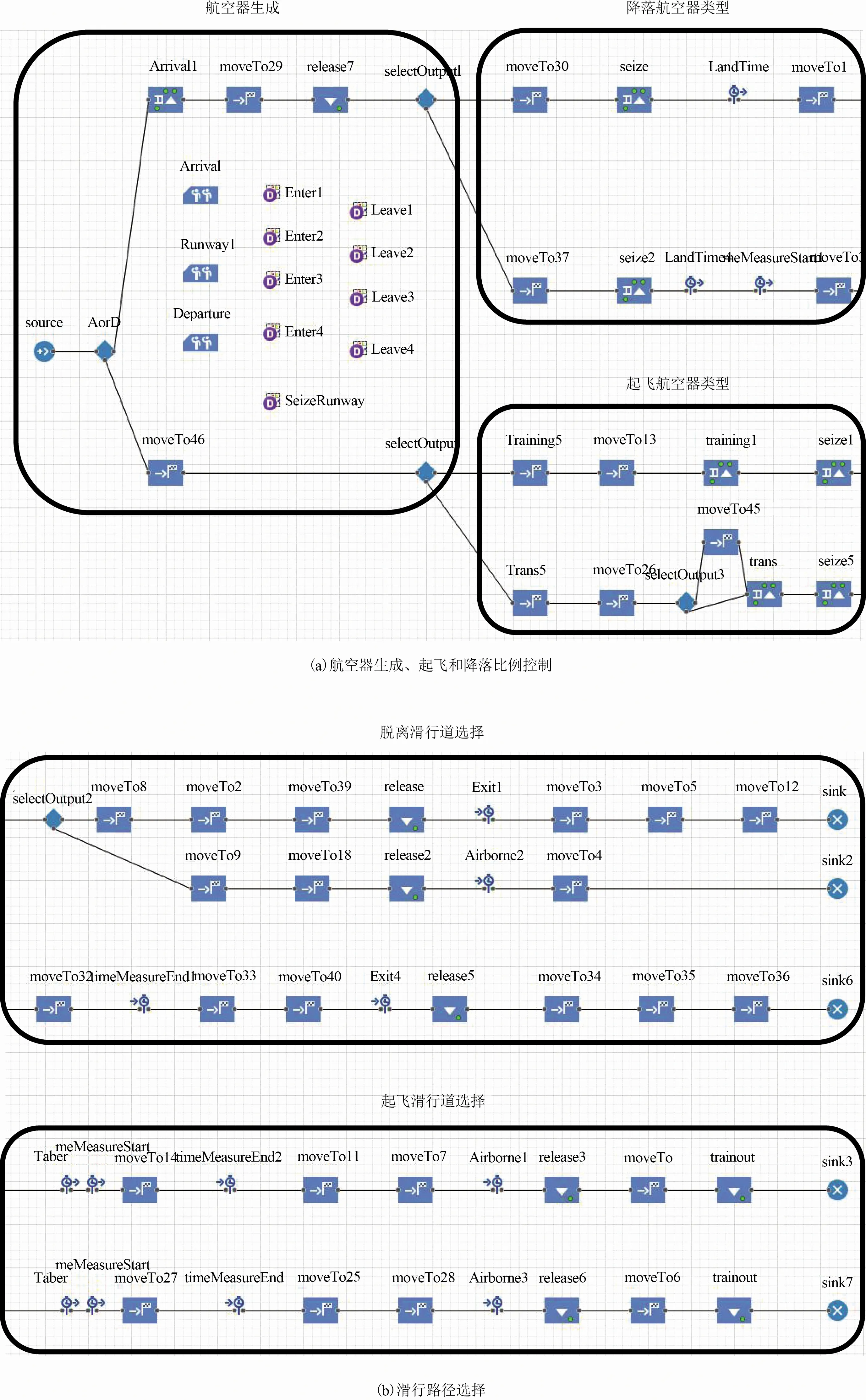
图4 Anylogic仿真模型控制模块Fig.4 Anylogic simulation model control modules

图5 Anylogic仿真模型运行界面Fig.5 Anylogic simulation run-time interface

图6 跑道服务能力随rb、rf变化趋势Fig.6 Runway capacity change with rband rf

在训练科目比例变化时，触地拉升占用跑道的时间TT&G=80 s，全停占用跑道时间为87 s，因此全停科目比例rf上升会使跑道服务能力P下降，导致单位时间跑道服务飞机数量减少。若固定训练飞行比例rb=0.3，当训练科目均为全停即rf=1时，跑道服务能力P为34.9架次/h；训练科目均为触地拉升即rf=0时，P为37.1架次/h；可见在同样的训练飞行比例下，改变训练科目比例可将跑道服务能力提升6%。

在航空器进离场活动均较多时，应控制训练飞行比例，保障运输飞行所需的机场关键资源，同时减少全停科目比例，选择触地拉升科目进行训练，有利于保障运输飞行和训练飞行的同时顺利开展。

3.2.3 起飞航空器比例和训练航空器比例对跑道服务能力的影响

设rf=0.5，rt=0.5，rb∈(0，1)，ra∈(0，1-rb)，rD∈(0，1)，rA∈(0，1-rD)，图7为训练科目比例固定，单位时间跑道服务能力P受rb和rD影响的变化趋势。

如图7所示，当rD=1，rb=0.5时，由于训练飞机采用减跑道起飞，后机起飞时需在2 min尾流间隔后多等待1 min，导致跑道服务能力降至最小，P仅为28.7架次/h。随着训练飞行的增加，得益于轻型机占用跑道时间少，跑道服务能力P缓增至30架次/h。在全为起飞航空器时，使用减跑道起飞相较于全跑道起飞跑道服务能力P降低了4.3%。

当rD∈[0.7，1]，rb∈[0，0.4]时，起飞航空器增加且训练飞行比例上升，前机训练飞机减跑道起飞，后机运输飞机等待时间延长导致跑道服务能力下降；当训练飞行比例继续上升，rb∈[0.4，1]时，由于训练飞机占用跑道时间短，可以一定程度上缓解前机减跑道起飞后机等待时间延长所造成的跑道服务能力下降，此时跑道服务能力P上升7.6%。

在运输飞行的离港高峰，应适当减少训练飞机的起飞数量，或先于出港高峰将训练飞机升空，尽量使起飞航空器比例控制在rD∈(0.2，0.5)，若航空器起飞比例较高则使用全跑道起飞。由于运输飞行每日起飞时间相对固定，故建议训练飞行起飞科目避开运输飞行出港高峰。

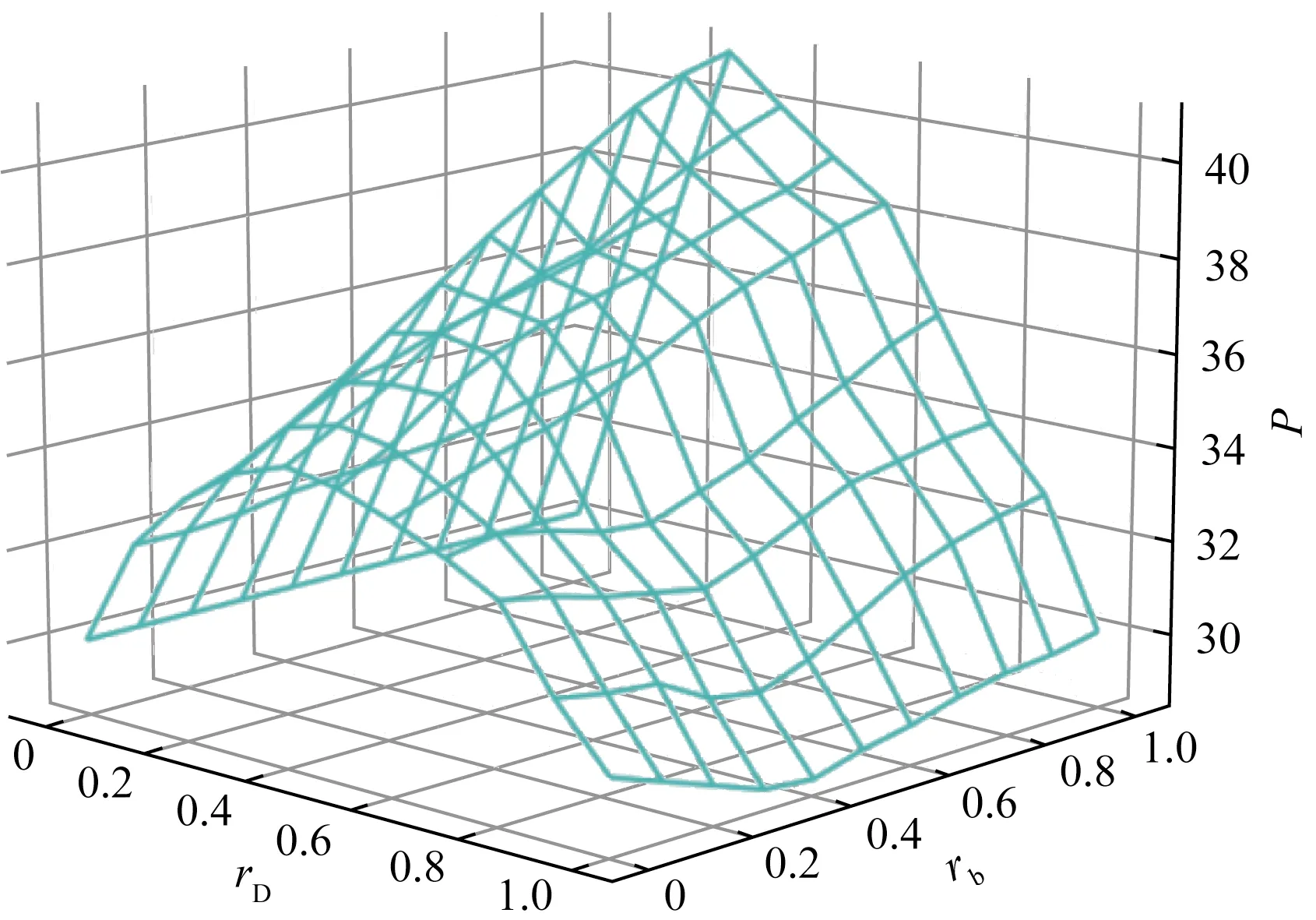
图7 跑道服务能力随rD、rb变化趋势Fig.7 Runway capacity change with rD and rb

3.2.4 起飞航空器比例和全停航空器比例对跑道服务能力的影响

设rb=0.7，ra=0.3，rf∈(0，1)，rt=(0，1-rf)，rD∈(0，1)，rA∈(0，1-rD)，图8为运输飞行与训练飞行比例固定，分析起飞航空器数量变化以及不同训练科目比例下，对于单位时间跑道服务能力P的影响。

如图8所示，在rD=0.3时，起飞航空器可以高效的插入降落航空器使用跑道的间隔进行起飞，此时跑道利用率大幅提高，取得跑道服务能力P为40.9架次/h。随着起飞航空器的继续增加，降落航空器落地间隔不足以满足所有起飞航空器的起飞时间需求，在rD>0.3后跑道服务能力逐渐下降。当所有飞行活动均为进港即rD=0时，由于尾流间隔的限制，跑道服务能力P降至最低为29.5架次/h，相较于rD=0.3起飞航空器高效利用降落航空器跑道使用间隔时，跑道服务能力P下降18%。由于Tland>TT&G，所以跑道服务能力P随着全停科目占比rf的升高而下降。

在运输飞行进港高峰，受制于尾流间隔限制，跑道使用会存在一定空窗时间，此时可以组织训练飞机完成起飞科目，将空窗时间最大程度利用。运输飞行班次相对固定，在组织训练飞行时应参考运输飞行排班，合理利用航空器降落后的跑道使用间隔，提高跑道服务能力。

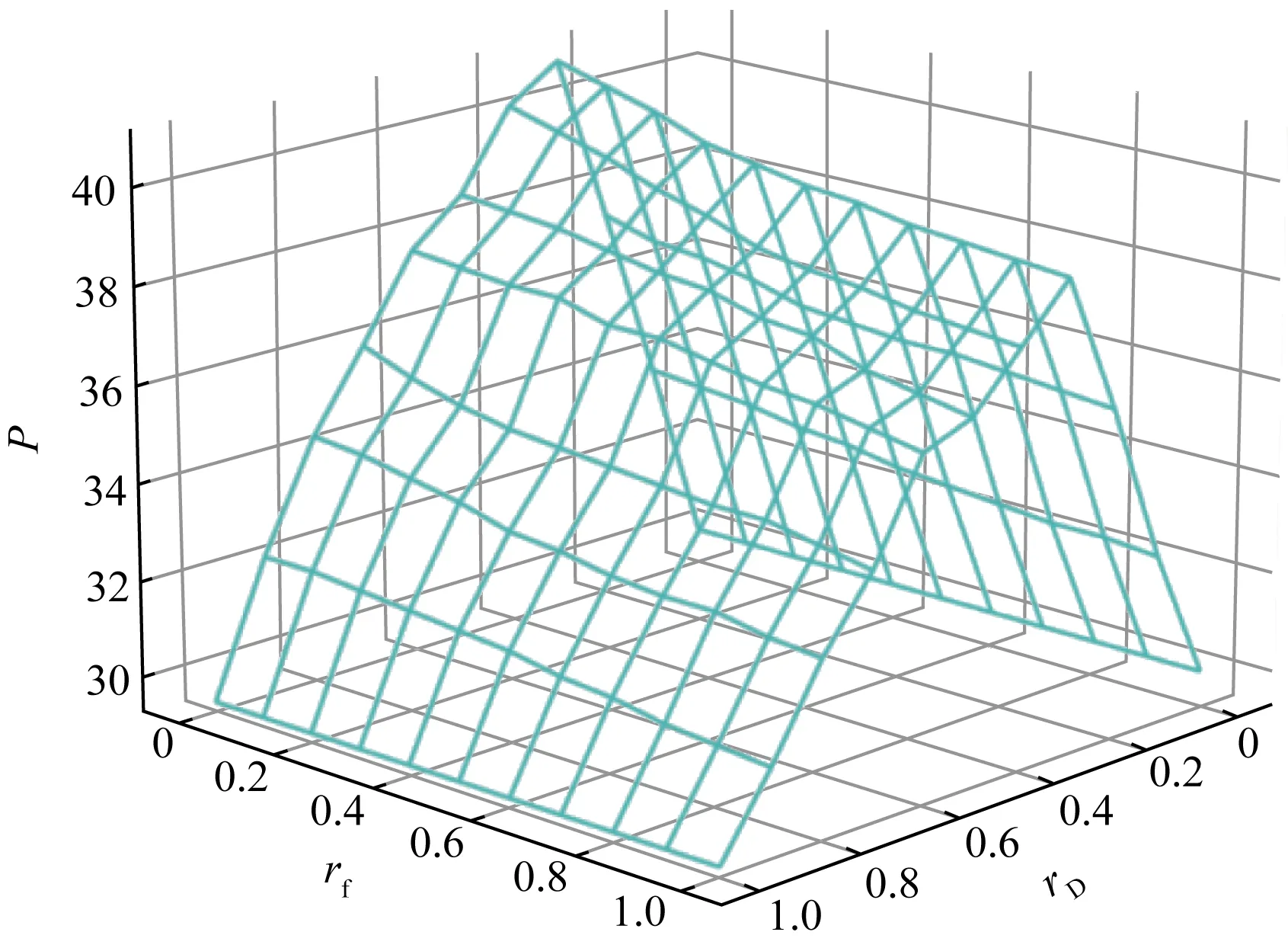
图8 跑道服务能力随rf、rD变化趋势Fig.8 Runway capacity change with rf and rD

4 结论

未来运输航班不断增长已成必然趋势，提升混合机场运行效率，根据运输飞行计划和训练飞行特点合理安排训练计划，对保障运输航班稳步上升和训练飞行正常开展具有重要意义。针对混合运输机场运行特点，分别量化运输飞行和训练飞行的占用跑道时间，结合不同训练科目，在此基础上建立混合运输机场跑道服务能力评估模型，使用Anylogic仿真软件进行仿真，根据关键参数变化对跑道服务能力的影响进行分析。根据仿真实验得出结论如下。

(1)在进离港活动均较多时，应首先保障运输飞行，控制训练飞行比例并增加触地拉升科目比例，可将跑道服务能力提升约6%。

(2)在离港高峰期，应减少训练飞行或将训练飞机提前升空，将起飞航空器比例控制在rD∈(0.2，0.5)。

(3)在进港高峰期，应利用航空器降落后的跑道使用间隔合理安排训练飞行起飞科目，可将跑道服务能力提升约18%。

仿真实验结果表明，本文模型能合理分析起降比例变化、飞行种类变化以及训练科目变化对混合运输机场跑道服务能力的影响，并针对机场运行过程中存在的高峰期提出相应建议。能够给存在运输飞行与训练飞行的混合运输机场未来提升跑道服务能力提供一定参考。