基于分解算法的动态大规模合乘匹配-路径规划
孙芮,吴文祥
(北方工业大学电气与控制工程学院,北京 100144)
随着经济发展与城镇化进程的加快,交通拥堵问题日益严重[1]。共享出行作为一种绿色出行方式,为城市走绿色可持续交通开拓新道路[2]。合乘问题近年来吸引了许多学者研究,研究目的是解决如何以尽可能小的出行成本实现最优匹配与路径规划,这类研究通常以匹配率、出行时间等为目标函数,建立合乘匹配与路径优化模型,根据模型特点设计相应的算法求解。
在合乘匹配与路径优化模型的研究中,Lee等[3]提出了使用专职司机为乘客提供服务的成本最小目标函数,结果表明合乘最具影响的因素有:合乘过程中参与者数量、参与者时间灵活性、参与者出发地与目的地的相似性。张亦楠[4]以路网的订单匹配率作为目标函数,利用粒子群算法求解。文献[5-9]以最小化出行成本、最大订单匹配率等作为模型的目标函数,对动态车辆调度问题进行优化。但上述研究中,大都考虑订单匹配率或乘客出行成本,不能在满足高匹配率的前提下,实现司机与乘客的低成本出行。
面对超大规模的订单数量,需要通过高效的算法来获得最终匹配方案和路径规划。学者们提出了各种算法来解决该问题,这些算法可以分为两类,精确算法和启发式算法。在精确算法的研究中:Duan等[10]提出了动态规划算法求解司机与乘客在不同区域下合乘匹配率。Armant等[11]在混合整数规划算法中引入约束规划公式,解决了使用累积约束和时间依赖性的问题,提高了合乘匹配率。Victoria等[12]分别采用列生成算法和整数规划算法,求解时变需求下具有时间窗容量限制的车辆调度问题。对中小规模实例测试结果表明,列生成算法比整数规划算法具有更好的效果。在启发式算法研究方面:Santos等[13]将一天时间进行划分,对每个时间段创建一个静态问题的实例,并用贪心随机自适应搜索程序(greedy randomized adaptive search procedures, GRASP)求解。Alonso-Mora等[14]提出了一种更通用的实时大容量合乘匹配模型,利用贪心算法求解最优合乘方案,基于纽约市出租车数据测试,该模型和算法可以有效解决大规模动态合乘问题。宋超超等[15]提出了一种粒子群算法求解动态合乘问题,结果表明该算法能够以较高的服务率与较低的成本完成车辆合乘匹配问题。在上述研究中,精确算法可以得到合乘的最优解,但搜索最优解会消耗过多的计算能力和存储空间。启发式算法效率较高,但无法找到真正意义上的最短路径,造成车辆绕道距离增大,导致本该匹配成功的司机与乘客不能成功匹配。
针对以上研究局限,所构建的合乘匹配模型考虑了订单匹配数量、司机旅行时间、乘客等待时间与乘客延误时间4个指标,满足高匹配率的前提下实现司机-乘客高质量匹配。针对模型特性,设计了基于分解方法的司机-乘客合乘匹配与路径规划算法。通过引入数据预处理模块减小合乘匹配问题的规模,设计分解算法将大规模合乘匹配问题分解为各个独立子问题迭代解决,加快平台对司机-乘客的匹配速度,实现司机-乘客的最优匹配。匹配完成后,调用百度API(application programming interface)线规划服务,获取司机-乘客合乘的最短路径规划。研究结果对缓解交通拥堵、推动合乘服务现代化发展以及降低出行者的出行成本具有重要的理论与现实意义。
1 问题定义与模型设计
首先详细描述动态合乘匹配问题涉及的基本概念。随后针对该问题,建立了带有约束条件的合乘匹配模型。
1.1 相关术语概念
对于合乘出行中,主要基本要素为:司机、乘客与平台。
定义1(司机)在动态合乘中,私家车司机用d表示,路网中司机的集合用D表示。司机向平台提交合乘请求,请求包含的属性有:起点与终点经纬度坐标、请求时间、起点出发时间窗、终点到达时间窗、车辆最大承载人数。
定义2(乘客)在动态合乘中,乘客用r表示,路网中乘客的集合用R表示。乘客向平台提交合乘请求,请求包含的属性有:起点与终点经纬度坐标、请求时间、起点出发时间窗,终点到达时间窗。
定义3(平台)在动态合乘中,平台每次更新信息,接收司机与乘客的合乘请求。平台在司机与乘客的出行时间窗内,将订单分配给司机,为司机规划行驶路线,最终完成司机与乘客的合乘行为。
1.2 模型设计
1.2.1 前提假设
提出的动态合乘匹配模型,做如下假设:①每辆私家车的最大承载能力是有限并预先给定的;②假设车辆的运行不受道路交通状况的影响,车辆以恒定车速行驶;③不考虑乘客的上下车时间;④在合乘出行过程中,一个司机能够服务多位乘客,但一位乘客只能被一个司机服务;⑤每位乘客与司机的出行信息都包含出行时间窗,出行时间窗代表从起点出发的时间窗与到达终点的时间窗。
1.2.2 集合
设D为司机的集合,R为乘客的集合,N为路网中节点的集合,A为路网中路段的集合。
1.2.3 决策变量

(1)
(2)
(3)
1.2.4 参数

1.2.5 模型建立

(4)
1.2.6 约束条件
(1)合乘模式的约束:
(5)
式(5)确保一位乘客只能被一位司机服务。
(2)节点约束:
(6)
(7)
式(6)、式(7)确保司机不能同时从两个不同的位置到达目的地,也不能同时到达两个不同的目的地[16]。
(3)车容量约束:
(8)
式(8)确保一辆车中所有乘客数量必须小于等于车辆的最大承载人数。
(4)司机出行时间窗约束:
(9)
(10)
式(9)、式(10)确保司机实际出发与到达时间分别满足出发时间窗与到达时间窗。
(5)乘客出行时间窗约束:
(11)
(12)
(13)
(14)
式(11)、式(12)确保乘客实际上车时间满足其出发时间窗,式(13)、式(14)确保乘客实际到达时间满足其到达时间窗。
(6)乘客与司机到达终点的次序约束:
tdd-[tdr+tdr,dd-M(1-adr)]≥0,
∀d∈D;∀r∈R
(15)
式(15)确保司机到达自己终点之前会将乘客送至其终点,其中M为一个非常大的值,保证司机与乘客成功匹配后才能验证该条件。
(7)司机总旅行时间约束:
(16)
式(16)确保该司机的总旅行时间小于等于司机能够在该行程中花费的最大时间。
2 基于分解方法的合乘匹配与路径规划算法
该节具体介绍基于分解方法的合乘匹配与路径规划算法。通过预处理筛选出司机能够潜在匹配的乘客集合,利用分解算法,将路网中所有司机匹配问题分解为各个独立的子问题进行最优匹配,最后调取百度地图API路线规划功能,获得司机行驶最短路径。
2.1 预处理
为了提高计算的效率,有必要在进行分解算法前对数据预处理,减小合乘匹配问题的规模,筛选出作为可行解的司机-乘客匹配方案。具体步骤如下。
Step 1初始化,记录路网中司机与乘客的起终点数据与出行时间窗。
Step 2数据预处理,根据司机与乘客的起终点,通过时空约束条件,筛选出司机d能够潜在匹配的乘客集合wd。
Step 3更新每位司机潜在匹配的乘客集合wd。
2.2 基于分解方法的合乘匹配与路径规划算法
2.2.1 基于分解方法的合乘匹配算法
为了提高算法的实时性,将路网中所有司机与乘客的合乘匹配问题,分解为各个独立的子问题迭代解决,具体步骤如下。
Step 1导入每位司机潜在匹配的乘客集合wd。



Step 5判断发生冲突的子问题中合乘质量大小,合乘质量最大的司机d获得服务该冲突乘客的优先权,其余司机选择次优的方案作为最优接送方案,若某位司机的所有接送方案中的乘客都存在冲突,则从wd中摘除该名乘客,跳转至Step 3,直至找到最优的司机-乘客匹配方案。
Step 6更新所有司机的接送方案。


图1 分解方法示意图
基于分解方法的合乘匹配算法能够将路网中所有司机与乘客的匹配问题,分解为各位司机最优匹配的独立子问题迭代求解,加快动态合乘中的匹配速度。该分解算法能够得到所有司机与乘客的最优匹配方案,方案包含了司机接送乘客的顺序,乘客所在节点等信息,是下一步动态路径规划算法的数据基础。
2.2.2 动态路径规划算法
通过分解算法,得到司机将要接送的乘客顺序与乘客所在节点的经纬度信息。司机从当下位置行驶至下一位位置的路径有多条,如何选择最短路径是该动态路径规划算法的研究内容。本文通过调取百度地图API中路线规划服务,获取车辆行驶的最短路径,具体步骤如下。
Step 1平台更新,判断司机d是否没有出发且期望发车时间小于当下时间,是,则该司机d信息重新进行动态匹配,否则跳转至Step 2。
Step 2判断车辆是否到达终点,如果是,记录并保存司机d行驶路径集合,该路径集合为司机d最短路径的集合,如果否,跳转至Step 3。
Step 3根据最优司机-乘客匹配方案,获取当下阶段车辆所在位置与将要行驶的下一个位置经纬度信息。
Step 4向百度地图API路径服务器发出请求,获取当下位置与下一个位置的可选路径集合,选择最短路径为车辆当下阶段要行驶的路径。
Step 5车辆向前行走一时步距离,在车辆行驶路线中记录当下行驶路径信息。
Step 6结束当下时步的操作。
3 实例分析
以成都市滴滴网约车订单数据为基础进行试验与分析,通过Python语言进行计算与结果图展示。
3.1 数据分析
为了比较乘客合乘上下车位置的时空分布,选择工作日中的12:00—18:00时间段的合乘数据进行分析。图2为乘客上车位置与下车位置的热力图。

图2 乘客上下车位置热力图
由于成都市“三环十六射”的路网结构,通过合乘的上下车位置热力图分析,入城与出城的热力分布较为显著。通过图2(a)可知,乘客的上车点有少部分集中在各入城路段周围,但多集中在环线以内,说明大部分乘客有出城的出行需求。乘客的下车点虽然很大部分集中在环线以内,但大量乘客的下车点分布在环线外[图2(b)],即出城路段的周围。图2表明合乘匹配的时空效果较好。
通过设置平台的更新时间为15 s,车辆最大承载能力为4人,路网中司机与乘客的比例为1∶3,调节优化模型中的3个权重指标α、β和γ,分析一周内网约车合乘数据在不同权重下的订单成功匹配率,结果如图3所示。

图3 不同权重下匹配率
由图3可知,一周内的乘客成功匹配率平均保持在80%以上。如图3(a)所示,当司机旅行时间的权重占比0.7,乘客等待时间与延误时间权重各占比0.15时,一周内每天8:00—20:00的匹配率稳定在85%以上,0:00—8:00与20:00—24:00的匹配率较低。如图3(b)所示,当司机旅行时间的权重占比0.5,乘客等待时间与延误时间权重各占0.25时,每天的平均匹配率稳定在70%~80%。如图3(c)所示,当司机旅行时间的权重占比0.3,乘客等待时间与延误时间权重各占0.35时,每天的匹配率呈现出明显的高峰与平峰,7:00—10:00匹配率高达90%以上,17:00—21:00匹配率也均在85%左右,而其余时间段的司机-乘客匹配率相比较低。
通过调节系统的更新时间、路网中车辆与乘客的比例,分析当下路网中车辆数与乘客数的改变对匹配率的影响,匹配率数据如表1所示。

表1 不同更新时间下的匹配率
由表1数据可知,随着更新时间的延长,司机-乘客匹配率有小幅度增长,但增长效果不明显。当路网中车辆数增多,司机-乘客匹配率有显著的增加,说明路网中能够服务乘客的车辆数量,对匹配率有着重要影响。
3.2 算法对比
在以往研究中,遗传算法、贪心随机自适应搜索算法与粒子群算法等广泛用于求解动态匹配与路径规划模型。通过选用求解效果较好的贪心随机自适应搜索算法、粒子群算法[13-15]与所提出的基于分解方法的合乘匹配与路径规划算法进行对比,分析本文算法求解动态规划模型的实际应用价值。数据选择工作日中7:00—9:00的合乘请求数据验证,算法对比结果如图4、图5所示。
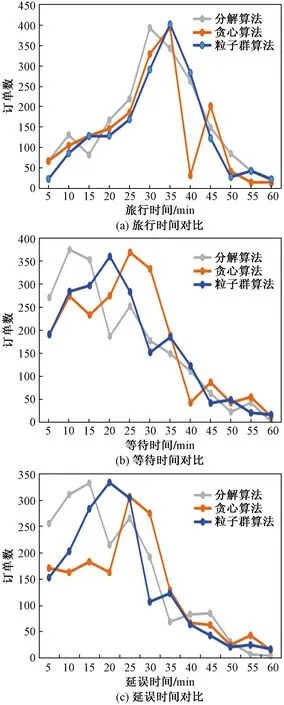
图4 不方便成本对比

图5 匹配率对比
如图4所示,基于分解方法的合乘匹配与路径规划算法结果优于粒子群算法与贪心算法。图4(a)中,3个算法的司机旅行时间峰值大多集中在30 min,但分解算法下旅行时间峰值明显小于30 min,说明该算法下司机旅行时间较短。图4(b)中,贪心与粒子群两个算法的乘客等待时间集中在15~30 min,但分解算法下大部分乘客等待时间在10 min以内。图4(c)中,贪心与粒子群算法的乘客延误时间峰值在20~30 min,但分解算法下乘客延误时间峰值在10 min左右。从司机与乘客的出行成本方面考虑,司机旅行时间短,有利于调动司机服务的积极性,乘客等待与延误时间短,会增加乘客在合乘中被服务的满意度,减少日后订单流失的概率,所以分解算法在实际中有较好的反馈效果。
由图5可知,随着平台更新时间的增加,3种算法的匹配率都随之增高,但分解算法的匹配率远在贪心与粒子群算法之上,总体匹配率远高于85%,表明分解算法能够保证路网中较高的匹配率。
综上,通过对所提出的基于分解方法的合乘匹配与路径规划算法与贪心随机自适应搜索算法、粒子群算法实例对比,结果表明,本文算法能够在平台更新时间内进行快速动态匹配,保证较高匹配率的基础上,实现高质量的司机-乘客匹配,提高整个路网的服务质量。
4 结论
针对现有动态合乘中司机-乘客匹配质量不高,算法实时性差等研究局限,构建了考虑订单匹配数量、司机行驶时间、乘客等待时间与乘客延误时间的合乘匹配模型,在保证高匹配率的前提下,提高司机与乘客在合乘过程中的满意程度。同时根据模型特点,设计了基于分解方法的合乘匹配与路径规划算法,将整个路网的司机-乘客匹配问题分解为各个独立的子问题迭代求解,提高了算法的实时性,加快了动态合乘匹配的效率。
现有研究中司机与乘客出行时间窗只在数据预处理时作为硬约束,日后可对出行时间窗进行分析,研究不同时间窗下对路网服务率的影响。经济因素也是司机与乘客选择合乘的原因之一,如何在合乘过程中对司机补贴以及乘客公平的定价,也是接下来研究的重点。

