基于背靠背变流器的风电系统仿真对比研究

刘建龙，郝正航

(贵州大学 电气工程学院,贵州 贵阳 550025)

近年来，随着全球能源需求的快速增长，可再生能源受到全世界的重视。在可再生能源中，风能储量丰富，分布范围广泛，能有效地缓解环境污染，逐渐被多国广泛开发利用[1-2]。

永磁同步电机(Permanent Magnet Synchronous Generator，PMSG)由永磁体提供励磁，无需励磁电流，具有结构简单、运行可靠、效率高等优点[3]。由PMSG所构成的永磁直驱风电系统中，包含了风力机、最大风能捕获和桨距角等模块。文献[4～6]针对上述模块的控制原理和特性进行了详细地分析研究。背靠背变流器是永磁直驱风电系统的关键，通过它可将变化的电压频率转化为恒定的电压频率，从而并入电网。文献[7～9]深入研究了背靠背变流器的结构及运行特性。文献[10～12]对风电系统的多种控制策略进行验证，以保证发电机输出的最大功率不超过系统的额定出力。目前系统接入背靠背变流器详细模型的常见方法增加了仿真系统的数学计算量，且波形中含有高次谐波。针对这一问题，文献[13～14]采用了变流器的均值模型，即由受控电源来代替变流器的详细模型。该方法忽略了变流器输出波形中的所有高次谐波，仅保留基波成分，且可采用大步长仿真计算。基于该条件，文献[15～17]在MATLAB/Simulink中建立了永磁直驱风电系统模型，可以准确地仿真系统各参量的运行特性。

基于改进的控制策略，本文对永磁直驱风电系统的平均值进行建模以减少数学计算量，加快仿真速度。最后，通过对比结果证实了均值模型和控制策略的有效性。

1 永磁直驱风电系统结构

永磁直驱风力发电系统中，风力机与永磁同步发电机直接耦合，省略了齿轮箱。由于风速具有随机、波动的特征，因此系统在并网时，PMSG定子通过背靠背变流器与电网连接，变化的电压频率被转换为恒定的电压频率。这样既提高了风电机组的可靠性与稳定性，又改善了电网波动的适应性。系统整体结构如图1所示。

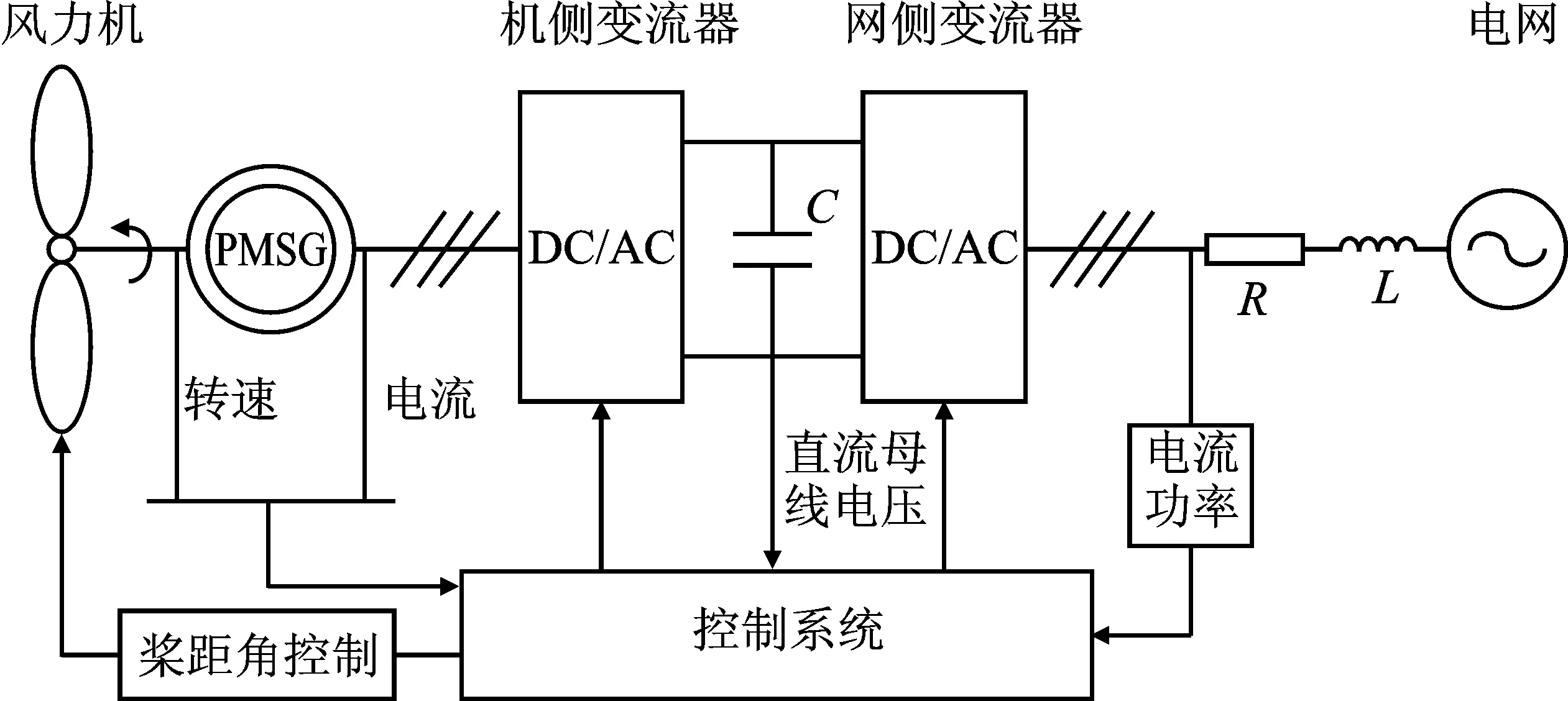
图1 永磁直驱风电系统整体结构框图

1.1 风力机特性模块

风力机的工作原理是将接收到的风能转化为机械能，并通过转轴输送出去。由空气动力学原理可知，风力机的输送功率Pw满足

(1)

式中，ρ为空气密度，单位为kg·m-3；R为风机叶轮半径，单位为m；β为叶片桨距角，单位为deg；λ为叶尖速比，即λ=ωwR/Vw；ωw为风力机转子转速，单位为rad·s-1；Vw为风速，单位为m·s-1。

风能利用系数为

(2)

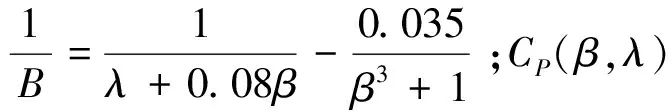
1.2 最大风能捕获模块

当实际风速小于额定风速时，变速风电机组根据系统的最大功率点跟踪(Maximum Power Point Tracking，MPPT)模块来完成系统的最大功率输出。

不同风速都有相应的功率曲线，当风速成λopt的比例变化时曲线达到峰值。连接曲线中所有的峰值即为最佳功率曲线Popt。

将λ=ωwR/Vw带入式(1)中，取最大风能利用系数Cpmax与最佳叶尖速比λopt，即可得式(3)。

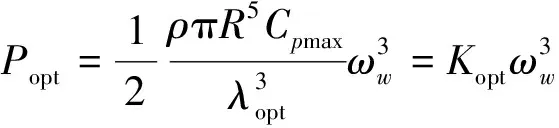
(3)

1.3 桨距角模块

当实际风速大于额定风速时，受设备容量等限制，必须降低风力机捕获的风能，使系统运行在额定值附近。因此风机叶片与风轮平面的夹角即桨距角开始增大，用来调整叶片的迎风角度，以此来限制捕获的能量，并使得发电机运行于最佳转速。而在实际风速小于额定风速时，桨距角通常取零。桨距角模块控制框图如图2所示。

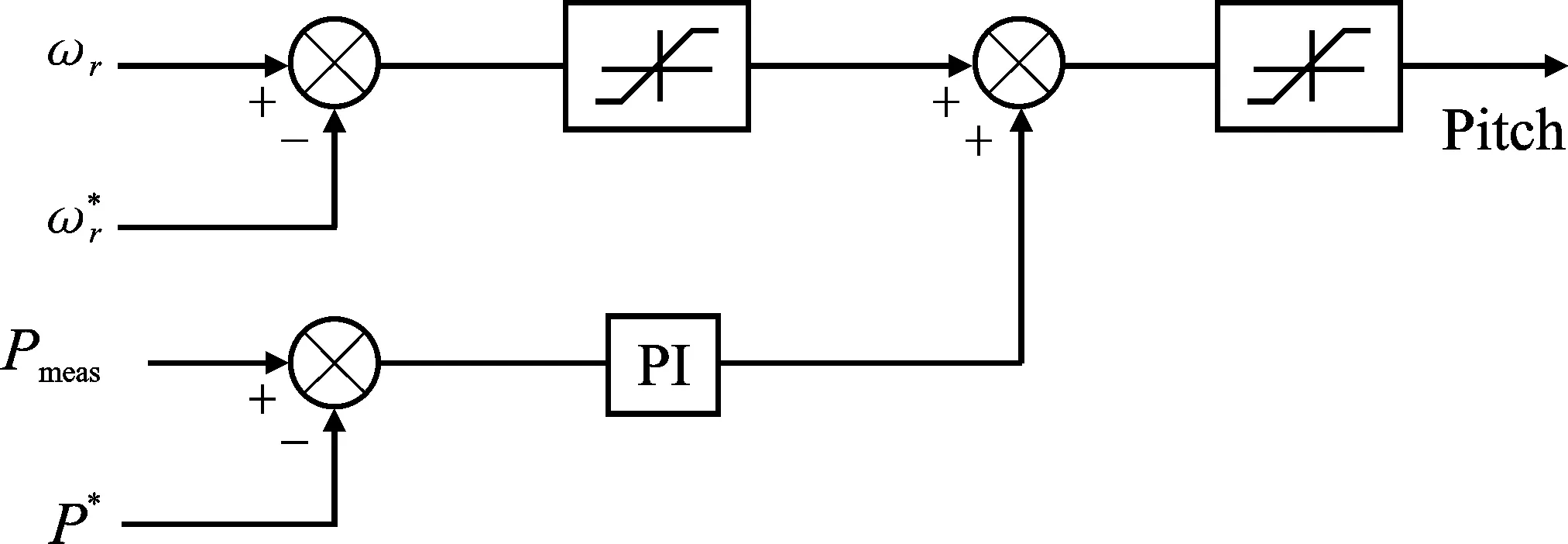
图2 桨距角控制框图

由图2可知，系统桨距角控制可分为两种方式：一种方式是控制实际转速和给定转速之间的差；另一种方式是通过PI来控制实际功率和给定功率之间的差。如果实际转速不等于额定转速，或者发电机超过额定功率时，则可调节桨距角以限制机组的输出功率在额定出力。

2 背靠背变流器详细模型

背靠背变流器详细模型在进行建模时，首先对每个电力电子开关器件进行单独建模，然后与实际拓扑电路结构结合以完成最终建模。该方法涉及了背靠背变流器里面所有开关的动作状态，各开关状态仅由自身的电压、电流和控制信号决定。在物理意义上，这种模型贴近于实际系统，但随着系统开关数量的增多，模型复杂程度也大幅增加，在大步长仿真下还可能出现内存溢出的现象。

根据文献[14]可得a点的相电压为

(4)

式中，调制比M=Us/Uc，Us为调制波电压，Uc为三角载波电压；载波比N=ωc/ωs，ωc为三角载波角频率，ωs为调制波角频率；Vdc为直流母线电压；m和n分别为相对于载波和调制波的谐波次数，谐波频率为(mN+n)ωs，其中m=2,4,…；n=±1,±3,…。式(4)同样适用于b、c点的相电压。

变流器详细模型的结构框图如图3所示。

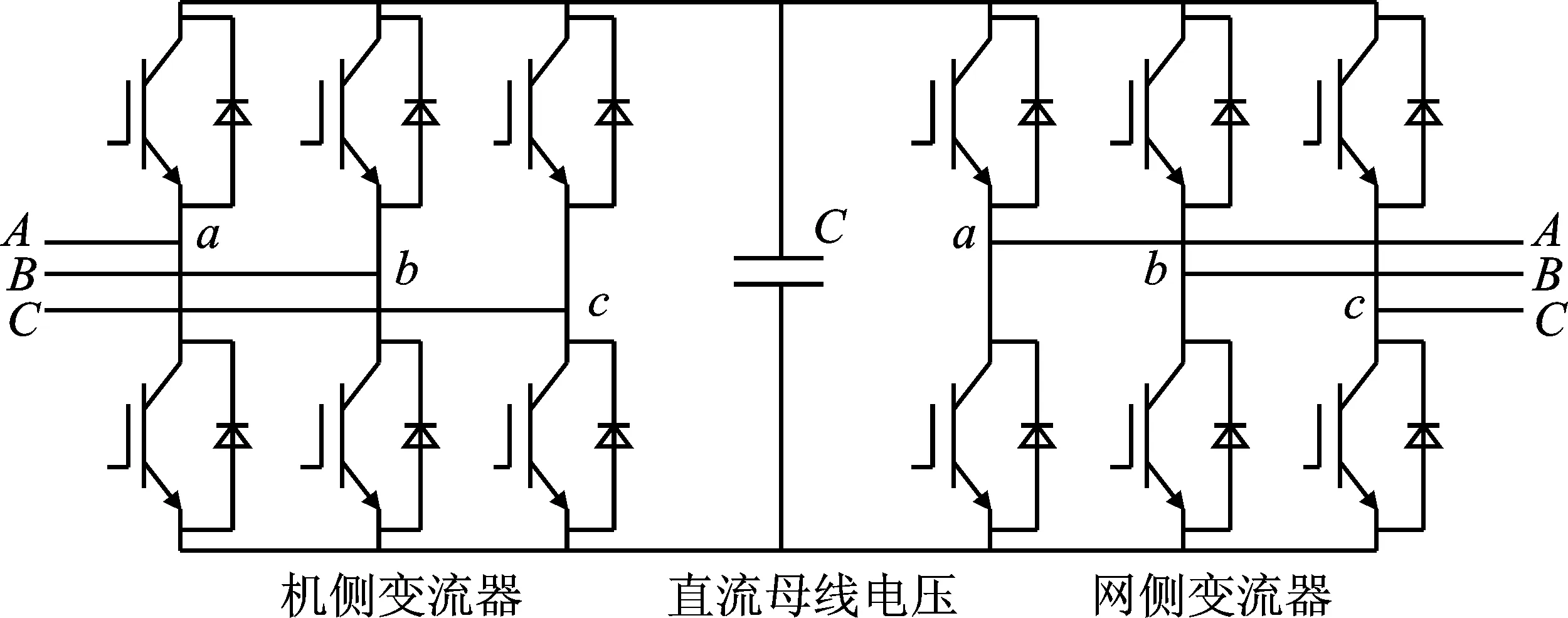
图3 变流器详细模型

详细模型中，首先将双闭环控制器输出的两相旋转电压信号进行坐标变换以获得三相电压信号；然后使用脉冲宽度调制(Pulse-Width Modulation，PWM)发生器获得控制 IGBT通断的开关信号；最后输出直流母线电压Vdc的波形。由式(4)可知，该波形不仅有基波成分，还存在大量的高次谐波。因此若要得到精确且稳定的输出，必须进行滤波操作，并且仿真时需采用较小的步长。较大步长会使得数值失稳，仿真速度慢，降低稳定性。

3 背靠背变流器均值模型

3.1 平均值建模

永磁直驱风电系统均值模型主要研究的是背靠背变流器。均值模型的原理是在一个开关周期內用变量的平均积分值代替实际值。平均值模型定义如下

(5)

式中，Ts为开关周期；¯x(t)为变量x(τ)在开关周期Ts内的平均值。

在变流器均值建模过程中，为了研究主要行为特性，通常会选择忽略一些次要因素。就结构而言，本文用受控电源替代了基于IGBT的变流器详细模型；原理上，它忽略了变流器输出波形的所有高次谐波，仅保留基波分量。

根据图3及PWM调制规律，可得受控电压源三相交流输出相电压Ua、Ub和Uc的基波分量为

(6)

(7)

(8)

式中，调制比M=Us/Uc，Us为调制波电压，Uc为三角载波电压；ωs为调制波角频率。

因为忽略了变流器损耗，那么交流侧与直流侧的有功功率Pac与Pdc应保持平衡，其关系表达式为

Pdc=Pac

(9)

由于三相交流有功功率为

Pac=UaIa+UbIb+UcIc

(10)

那么直流侧有功功率为

Pdc=UaIa+UbIb+UcIc

(11)

因此可得直流电流为

(12)

故受控电压源控制信号为式(6)～式(8)，受控电流源控制信号为式(12)。变流器均值模型的结构框图如图4所示。

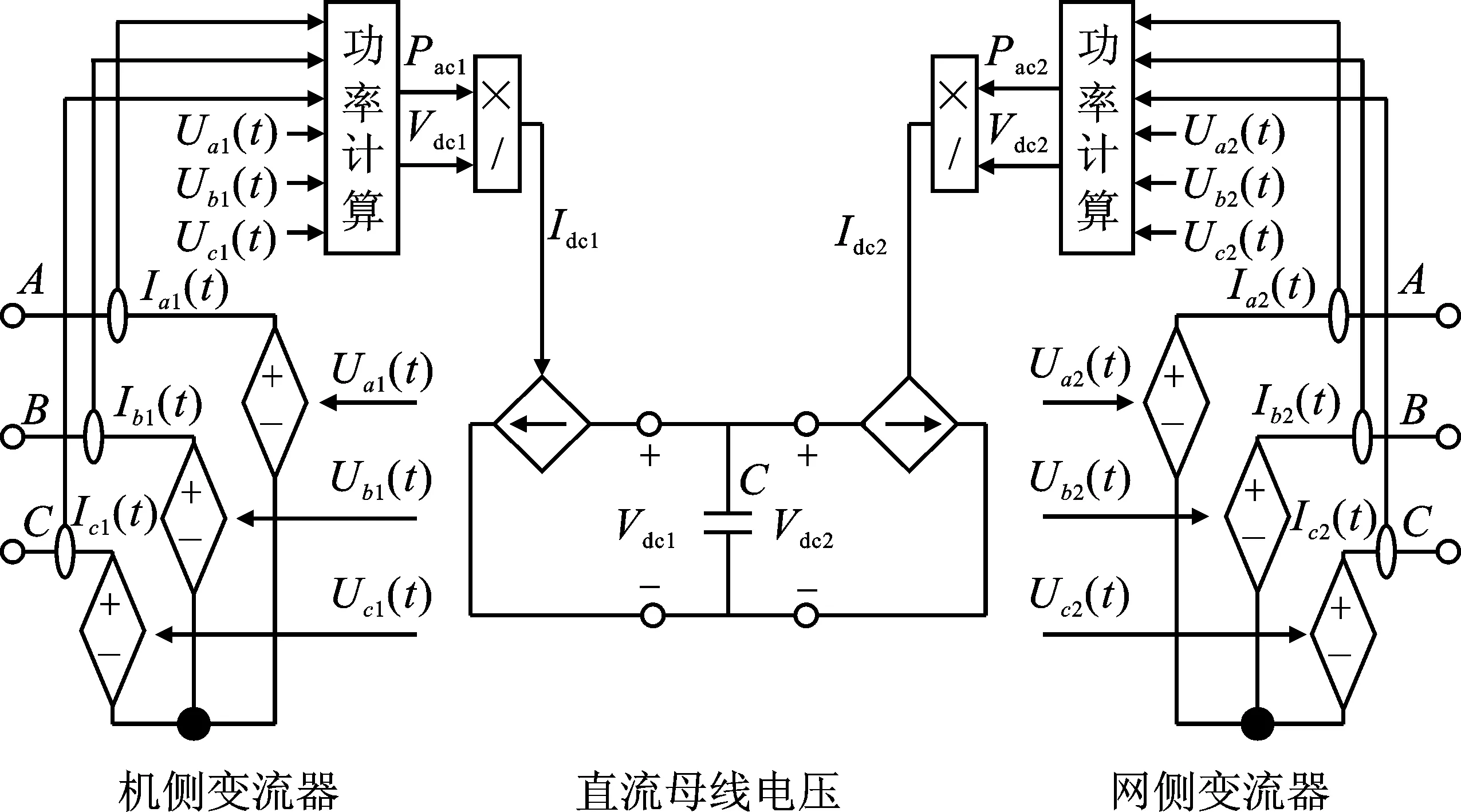
图4 变流器均值模型

均值模型中，双闭环控制器输出的两相旋转电压信号通过坐标变换以获得三相电压信号。此信号直接用作控制受控电压源的控制信号来代替详细模型的PWM开关信号，省略了PWM调制过程，减少了数学计算量。最后通过式(12)，以直流电流Idc作为受控电流源的控制信号得到直流母线电压Vdc的波形。该模型采用较大步长进行仿真，输出波形也只有基波成分，不含有高次谐波，无波形畸变，故仿真速度较快，稳定性较高。

3.2 系统改进控制策略

在系统详细模型的控制策略中，双闭环控制器的输出是先经过坐标变换，然后再经过PWM调制去产生开关信号。在均值模型中，是将双闭环控制器输出的电压信号经过dqo-abc的坐标变换后直接作用于受控电源，不需要经过PWM调制，减少了数学计算量，使得系统控制策略更加简单高效。

3.2.1 网侧变流器控制策略

网侧变流器主要用于维持直流母线电压的稳定和实现有功、无功功率的解耦。因此，控制策略采用面向电网电压定向矢量控制方法。

将电网电压综合矢量置于d轴上，那么q轴上投影为0，即vqg=0。因此网侧变流器与电网之间交换的有功功率Pg和无功功率Qg为

(13)

由式(13)可知，在电网电压恒定的情况下，瞬时有功功率Pg和无功功率Qg分别与电流分量idg和iqg呈线性关系，因此仅控制d、q轴的电流分量就可以实现对有功和无功功率的控制。

两相旋转d-q坐标系下的网侧变流器数学模型为

(14)

式中，vdg为电网电压的d轴分量；idg和iqg分别电网电流的d、q轴分量；vdo和vqo分别为网侧变流器出口电压的d、q轴分量；Rg和Lg分别为网侧电阻和电感；ωg为电网同步电角速度。

由式(14)可以看出，网侧变流器出口电压vdo、vqo之间存在耦合项ωgLgiqg和-ωgLgidg，因此本文将它们作为前馈补偿来消除两者之间的耦合，此处为完全补偿。

将式(14)改写如下

(15)

(16)

由式(16)可知，可以采用如下所示的PID控制器

(17)

直流侧电容输入的瞬时有功功率

P=idcUdc

(18)

当电网电压不变且忽略变流器损耗时，那么直流侧与交流侧的有功功率应相等，即

(19)

由式(19)可知，通过控制电流分量idg可实现对vdc的控制。因此，使用PID控制器，可直接由直流母线电压vdc的参考值来得到电流分量idg的参考值，如

(20)

据此，网侧变流器控制结构框图如图5所示。

图5 网侧变流器控制框图

3.2.2 机侧变流器控制策略

机侧变流器基于最佳叶尖速比控制，通过调节发电机转速实现风电机组最大风能跟踪。

发电机电磁转矩方程

Te=1.5PnΨs×is

(21)

将Ψs=Ψd+jΨq和is=id+jiq带入可得

Te=1.5Pn[Ψfiq+(Ld-Lq)idiq]

(22)

当id=0时，式(22)可简化为

Te=1.5PnΨfiq

(23)

式中，Pn为极对数；Ψf为转子磁链。

由式(23)可知，对于转子磁链和极对数一定时，电磁转矩Te与定子电流分量iq成正比，也就是Te仅由iq唯一控制。因此，控制策略采用零d轴电流控制方法。

PMSG在d-q坐标轴下的定子电压方程为

(24)

式中，ud、uq、id、iq分别为定子等效的d、q轴电压和电流；Ld、Lq分别为定子绕组的d、q轴电感；Rs为定子相电阻；Ψf为转子磁链；ωr为转子旋转的电角速度。

根据式(24)可以看出，定子电压分量ud、uq之间存在耦合项-ωrLqiq和ωrLdid，因此将它们作为前馈补偿来消除两者之间的耦合，此处为完全补偿。

将式(24)改写如下

(25)

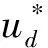
(26)

由式(26)可知，可以采用如下所示的PID控制器

(27)

发电机运动方程

(28)

根据式(28)可知，发电机的转子转速ωm与电磁转矩Te有关，而式(23)中电磁转矩Te又与电流iq有关，故可通过转速参考值来得到电流iq的参考值。其采用的PID控制器如下所示

(29)

据此，机侧变流器控制结构框图如图6所示。

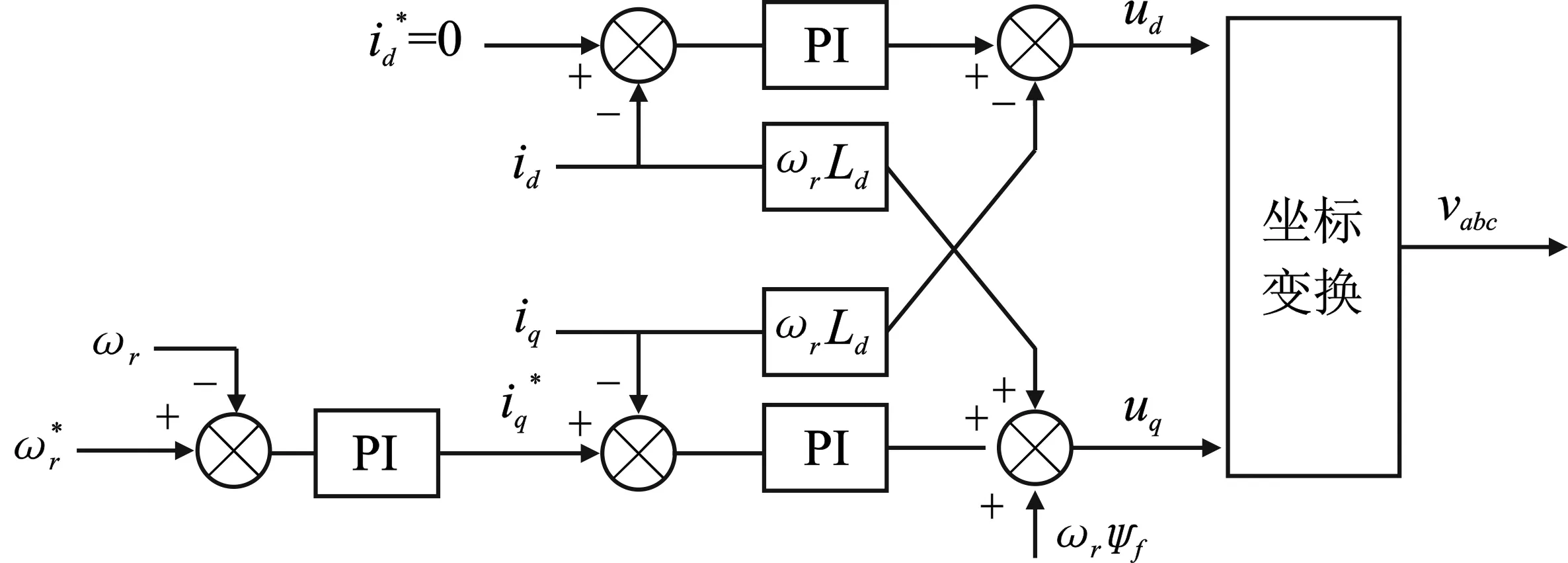
图6 机侧变流器控制框图

4 系统仿真与分析

4.1 系统模块参数设置

永磁直驱风电系统机组参数如表1所示。

表1 风电机组参数

仿真基本风速为4 m·s-1，在0 s时合上并网开关；在10 s时，启动网侧变流器；在15 s时，启动机侧变流器；在20 s时，风速由4 m·s-1升至额定风速11 m·s-1；在25 s时，风速由11 m·s-1升至最大风速15 m·s-1。

4.2 仿真分析

为了验证变流器模型的仿真精度和速度，利用MATLAB/Simulink构建永磁直驱风电系统并网模型。

4.2.1 变流器模型仿真精度验证

为了验证变流器模型的仿真精度，分别取变流器的均值模型与详细模型进行对比分析。其永磁直驱风电系统各参量的仿真结果如图7～图13所示。

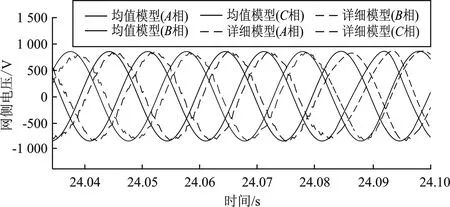
图7 网侧电压对比

图8 直流母线电压对比

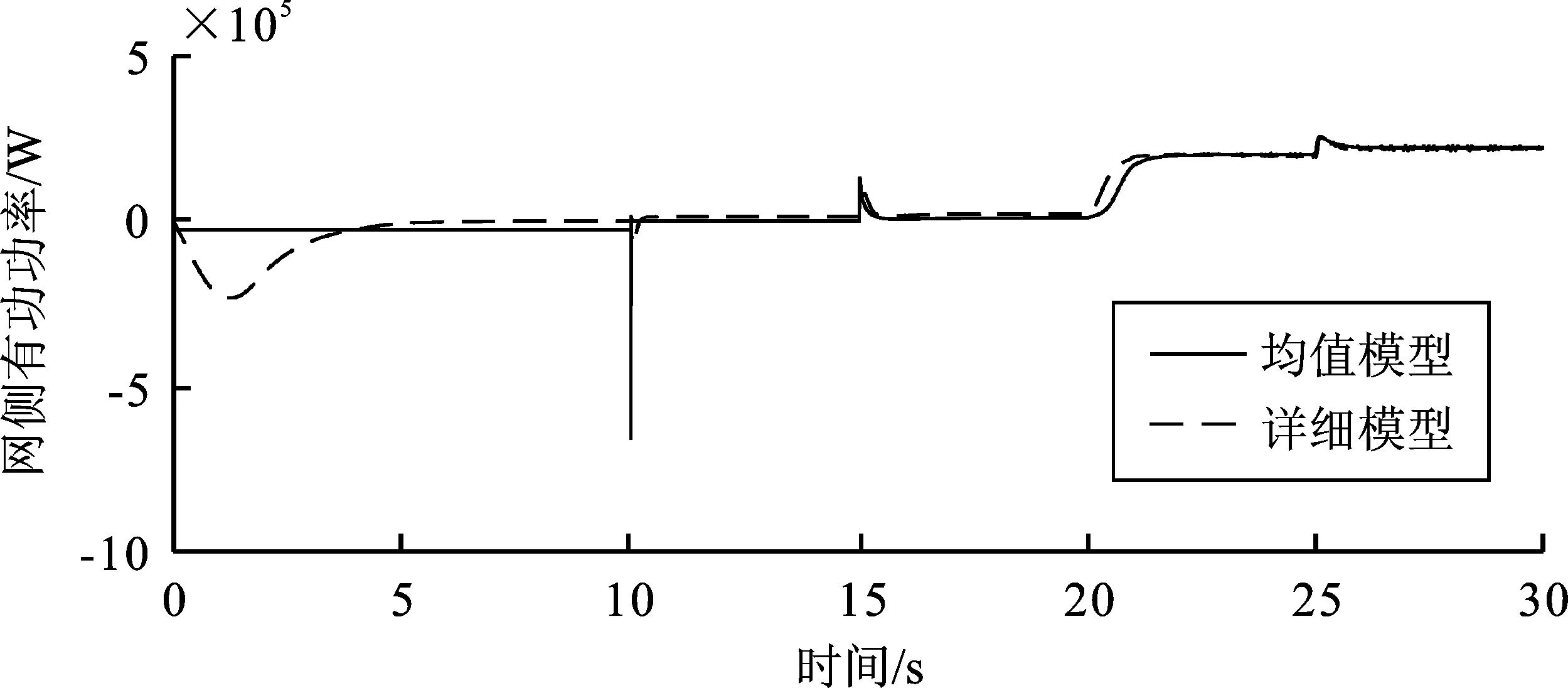
图9 网侧有功功率对比

图10 网侧无功功率对比

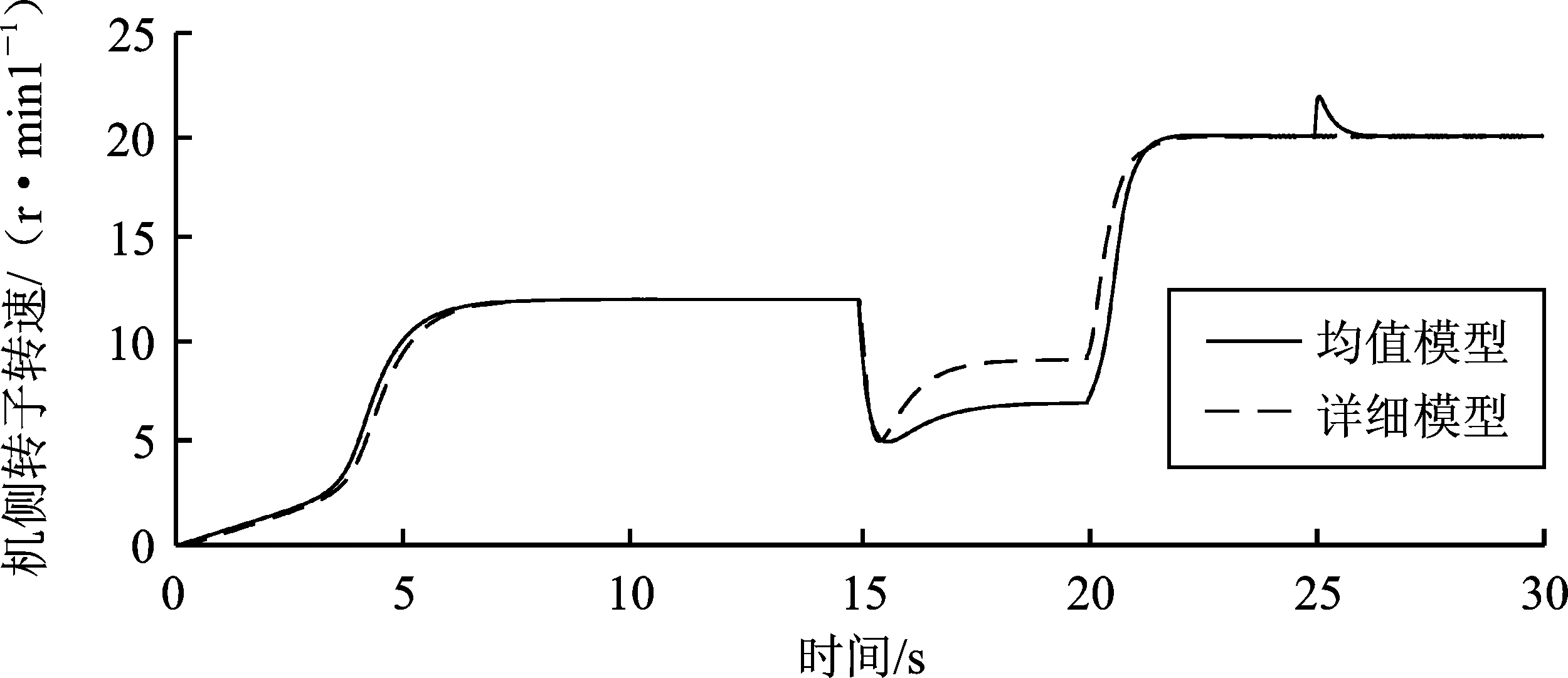
图11 机侧转子转速对比

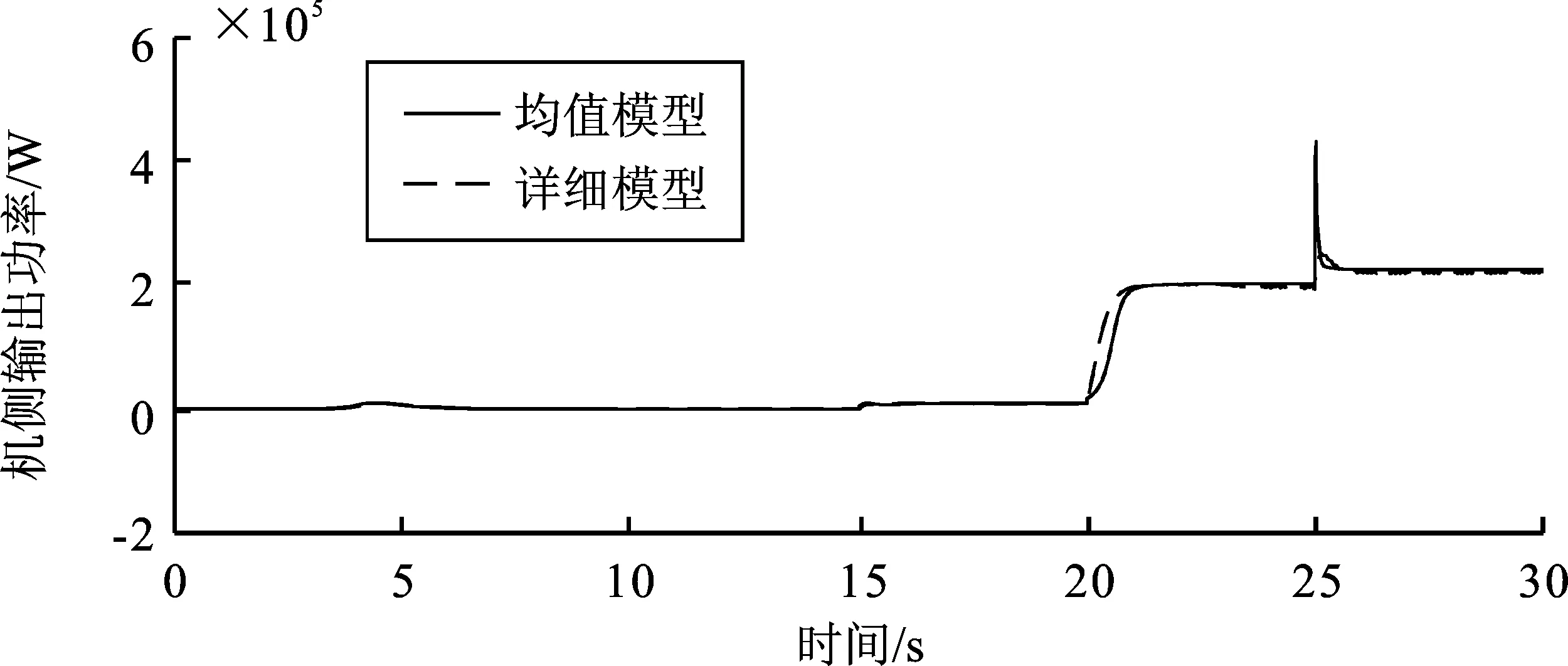
图12 机侧输出功率对比

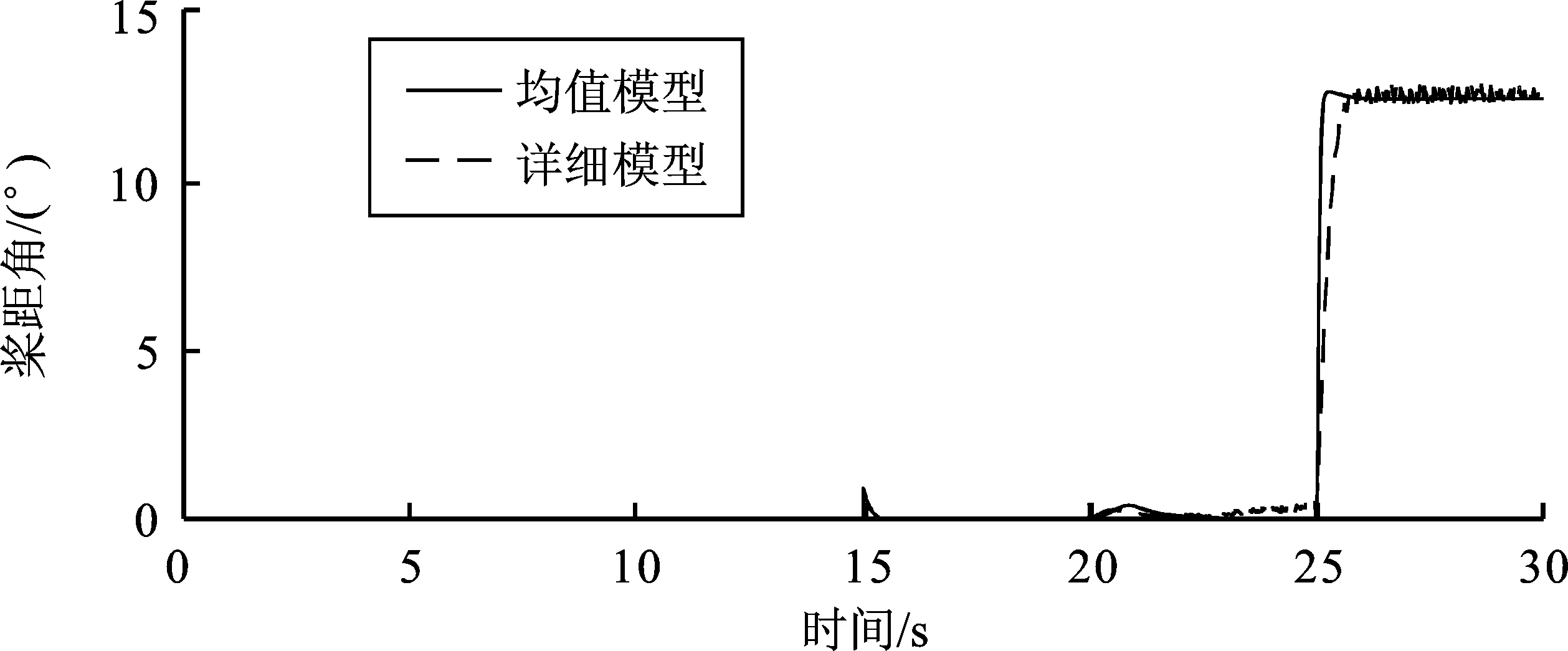
图13 桨距角对比

从图7～图13的系统仿真结果波形对比可知，永磁直驱风电系统的均值模型各参量的波形曲线与其详细模型在一定误差范围内近似一致。从波形的后段曲线可以看出，虽然详细模型各模块的输出均已进行滤波处理，但仍存在明显的数值失稳现象；而均值模型的波形则更接近于理想波形。

4.2.2 变流器模型仿真速度验证

为了验证变流器模型的仿真速度，分别取变流器的均值模型与详细模型进行对比分析，永磁直驱风电系统仿真时间如表2所示。

表2 仿真时间分析

由表2中的数据可以看出，均值模型在仿真速度上具有明显的优势。随着仿真步长的逐渐增大，详细模型会发生波形畸变的现象，而均值模型的优势更加突出，仿真时间更短。

4.2.3 系统运行过程分析

系统运行时，在0～10 s内，首先对电容进行充电，以保护器件。在10 s时，启动网侧变流器，之后将直流母线电压良好地稳定在了750 V，并且网侧无功功率保持为零。在10 s后，发电机的输出功率几乎为零，且转子转速保持在12 r·min-1左右，这可能是由于转速太快而无法输出功率。在15 s时启动机侧变流器，MPPT开始工作，寻找最大功率点，发电机转子转速降低至7 m·s-1，此时输出功率大约为0.01 MW。在20 s时，风速增大至额定风速11 m·s-1，发电机转子转速升至20 r·min-1，且输出功率上升至0.202 5 MW。在25 s时，风速上升至15 m·s-1，已超过了额定风速，此时风力机桨距角开始工作由0°升至12.35°，以此将捕获的风能限制在额定输出功率0.225 MW，并且发电机的转子转速保持20 r·min-1不变，保证了风机运行安全，并实现了最大风能捕获。

5 结束语

本文以永磁直驱风电系统为背景，分别对系统中背靠背变流器的详细模型与均值模型进行了分析研究，给出了变流器均值模型的建模方法。本文建立了发电机侧与电网侧的数学模型，并提出了相应的系统改进控制策略。最后通过MATLAB/Simulink验证了系统模型和控制策略的有效性和可行性。仿真结果表明，均值模型不仅能满足系统精度要求，还能加快系统仿真速度，有效提升了系统的稳定性，解决了详细模型中数学计算量大和含有高次谐波分量的问题，有利于系统高质量地稳定运行。