扫描平面向量中的解题误区

■杨 立 刘大鸣（特级教师）

平面向量融“数”与“形”于一体，具有几何与代数的“双重身份”，它是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景。下面汇集了同学们在求解向量问题中的常见错误，并剖析其原因，展示其正解，希望对同学们的学习有所帮助。

误区1：忽视零向量的特殊性

例1已知向量a＝（3，2－m）与b＝（m，－m）平行，则m值的个数是______。

错解：由a∥b得，即m2－5m＝0，解得m1＝5，m2＝0（舍去），所以m值的个数是1。

正解：零向量与任一向量平行，当m＝0时，b为零向量，也与a平行。由a∥b得3（－m）－m（2－m）＝0，解得m1＝5，m2＝0，所以m值的个数是2。

警示：零向量的模为0，记作0，其方向是任意的，0 与任意向量平行。零向量的性质有:0·a＝0，0＋a＝a。在判断向量有关命题的真假时，不能遗漏零向量。

误区2：忽视两个向量的夹角

例2等边△ABC的边长为1，设，则a·b＋b·c＋c·a＝______。

错解：由等边△ABC的边长为1，可得a·b＋b·c＋c·a＝1·1·cos60°＋1·1·cos60°＋1·1·cos60°＝。

正解：题中向量a与b的夹角是120°，而不是60°，错解把两个向量的夹角与三角形的内角混淆了。在等边△ABC中，a与b的夹角为120°，b与c夹角为60°，c与a夹角为60°，所以a·b＋b·c＋c·a＝1·1·cos120°＋1·1·cos60°＋1·1·cos60°＝。

警示：利用向量可以平移的特点，将两向量平移到从同一定点出发的两个向量的正方向所夹的角即为两向量的夹角。需要注意的是:两向量夹角的取值范围是[0，π]。

误区3：混淆一个向量在另一个向量方向上的投影

正解：上述解法混淆了一个向量在另一个向量方向上的投影，结果求得的是向量a在b方向上的投影。

误区4：忽视向量数量积与实数乘法的区别

例4已知a，b都是非零向量，且向量a＋3b与7a－5b垂直，向量a－4b与7a－2b垂直，求向量a与b的夹角θ的值。

错解：由已知两个向量垂直得据此化简整理得两式相减得46a·b－23b2＝0，即b（2a－b）＝0，所以b＝0（不合题意）或2a－b＝0。由2a－b＝0知a与b同向，故向量a与b的夹角θ＝0°。

正解：对于实数a，b，若ab＝0，则a＝0或b＝0，但对于向量a，b，若a·b＝0，则不一定有a＝0 或b＝0。由a·b＝|a|·|b|cosθ知，当θ＝90°时，a·b＝0也成立，此时a，b均可以不为0。

据此可知，把b2＝2a·b代入7a2＋16a·b－15b2＝0 得a2＝2a·b，所以a2＝b2＝2a·b，所以cosθ＝。又θ∈[0，π]，故所求夹角θ＝60°。

警示：向量的数量积运算不满足结合律，也不满足消去律。

误区5：误认为a 与b 的夹角为钝角(锐角)⇔a·b＜0（＞0）

例5已知向量a＝（2，1），b＝（λ，1），λ∈R，a与b的夹角为θ。若θ为锐角，则λ的取值范围是______。

正解：当cosθ＝1 时，θ＝0°，也满足cosθ＞0，但θ不是锐角，不合题意，所以要排除两向量共线且同向的情况。

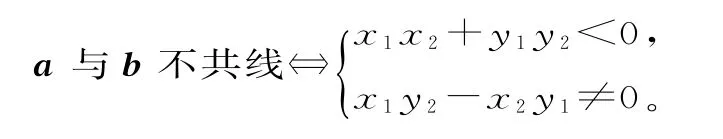
误区6：混淆共线向量或三点共线的条件

例6已知同一平面上的向量a，b，c，两两所成的角相等，且|a|＝1，|b|＝2，|c|＝3，求向量a＋b＋c的长度。

错解：易知a，b，c皆为非零向量。设a，b，c所成的角均为θ，则3θ＝360°，即θ＝120°，所以a·b＝|a|·|b|cos120°＝－1。同理可得，b·c＝－3，c·a＝－。因为|a＋b＋c|2＝a2＋b2＋c2＋2a·b＋2b·c＋2c·a＝3，所以|a＋b＋c|＝。

正解：当向量a，b，c共线且同向时，所成的角也相等，均为0°，也符合题意，这时|a＋b＋c|＝|a|＋|b|＋|c|＝6；当向量a，b，c不共线时，由错解得|a＋b＋c|＝。综上所述，向量a＋b＋c的长度为6或。

警示：处理共线向量有关问题时，一定要注意向量的方向。若（λ，μ为常数），则A，B，C三点共线的充要条件是λ＋μ＝1。

感悟与提高

图1