基于两种不同预测方法的广西人口预测

唐璐薇，吕 超，潘玉婷，陈 璟

（广西科技师范学院 数学与计算机科学学院，广西 来宾 546199）

本研究以2011—2020年广西全区农村人口、城镇人口和年末常住人口为基础，运用BP神经网络和时间序列ARIMA（p，d，q）预测模型，对2021—2036年广西全区农村人口、城镇人口和年末常住人口进行预测，证实了两种预测模型的有效性，进而为相关部门制定相应的政策措施提供依据.

1 模型的建立

1.1 BP神经网络

BP（back propagation）神经网络是1986年由Rumelhart和McClelland为首的科学家提出，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一［15］.有关研究表明，有一个隐层的神经网络，只要隐节点足够多，就可以以任意精度逼近一个非线性函数.因此，本研究采用含有一个隐层的三层多输入多输出的BP网络建立预测模型，模型的建立如下：

输入数据为2011—2020年广西全区农村人口、城镇人口和年末常住人口数，（1）输入层到隐层的一个模型，假设是第h个隐层神经元的输入

（2）隐层到输出层的一个模型，得到我们2021—2036年的人口预测数据，

我们通过以上的模型，运用MATALB编程将数据代入，根据BP神经网络求解步骤，可得到2021—2036年广西人口总数的预测.其具体结构如图1所示.

图1 BP神经网络多输入多输出拓扑结构图

BP神经网络求解的步骤如下：第一步，选择训练集和检测集；第二步，构建一个神经网络；第三步，用训练样本对网络进行训练；第四步，对检测样本进行仿真模拟；第五步，评价拟合效果；第六步，求出未知的待检测样本.

遂昌金矿国家矿山公园位于浙江省丽水市遂昌县东北部，距遂昌县城16公里。公园于2005年7月由国土资源部批准建立，成为全国首批28家国家级矿山公园之一，是全国唯一挂牌“中国黄金之旅”的景区。公园总面积33.6平方公里，矿业展览区面积6.3平方公里。

1.2 ARIMA（p，d，q）模型的建立

人口数量是随着时间不断变化的，但是人口和时间的关系不能用简单的线性回归多项式来表示，为了更好地对人口进行预测，本研究运用了时间序列中的ARIMA（p，d，q）模型，模型的输入数据为2011—2020广西城镇人口数、农村人口数和年末人口总数，用来预测2021—2036年年末广西人口总数.本研究的数据序列假设经过差分后，得到的序列为平稳序列.假设其时间序列具有明显的线性趋势，则可以设其模型为：

2 模型求解预测广西人口

2.1 BP神经网络模型求解

2.1.1 数据集本研究数据来源于国家统计局官网中人口普查数据的统计，包括2011—2020年广西全区农村人口、城镇人口和年末常住人口的数据.

2.1.2 数据分组

本研究将数据分为训练集和检测集，将原始数据从2011—2015年的数据归入训练集，其余所有数据作为检测集；对检测集的数据进行预测，以测算预测精度来判断，预测精度越接近于1，拟合效果越好，以此对2021—2036年的人口相关数据进行预测.

为了更好地预测人口数，在进行BP神经网络预测前，本研究将数据进行了归一化处理，归一化处理后的人口数与原始数据对比散点图如图2所示，其中第一列图为归一化处理后的图形，第二列图为原始数据图形.

图2 原始数据归一化比较图

由图2可知，归一化后的数据基本保持了原始数据的走势规律，这说明归一化不改变数据要表达的原始意义.接着，运用收集到的人口数据，采用BP神经网络进行预测，发现预测精度为99.05%，接近于1，说明BP神经网络的预测效果良好.可视化的展示如图3所示.

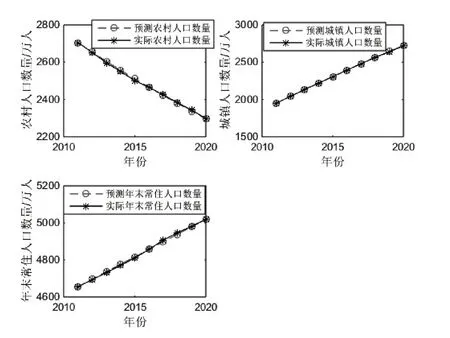
图3 广西年末实际农村人口、城镇人口和常住人口与预测人口曲线图

由图3可知，运用BP神经网络对2011年到2020年的广西农村人口、城镇人口和年末常住人口进行预测，经过与实际人口数量对比可知，两条曲线接近于重合，说明本研究运用BP神经网络预测效果良好.

由图4可知，本研究通过对2021—2036年广西年末常住总人口的预测，到2036年末广西常住总人口将突破5685万，且农村人口在不断减少，而城镇人口在逐年增多，这说明广西的城镇化水平逐年提高.另外，由年末常住人口呈上升趋势来看，广西的发展水平也在逐年提升，更多的人愿意留在广西生活.结合广西统计年鉴对2021年年末广西总人口的统计数，我们发现，运用BP神经网络的预测效果良好，与实际数据较接近.具体的人口预测数如表1所示.

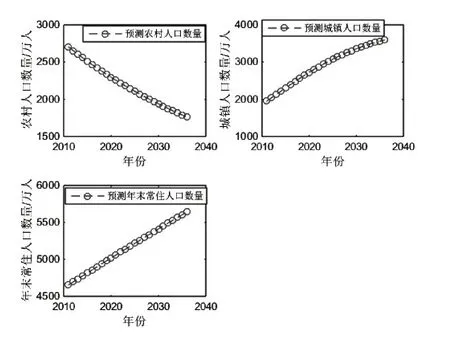
图4 2021—2036年广西农村人口、城镇人口和年末常住人口预测图

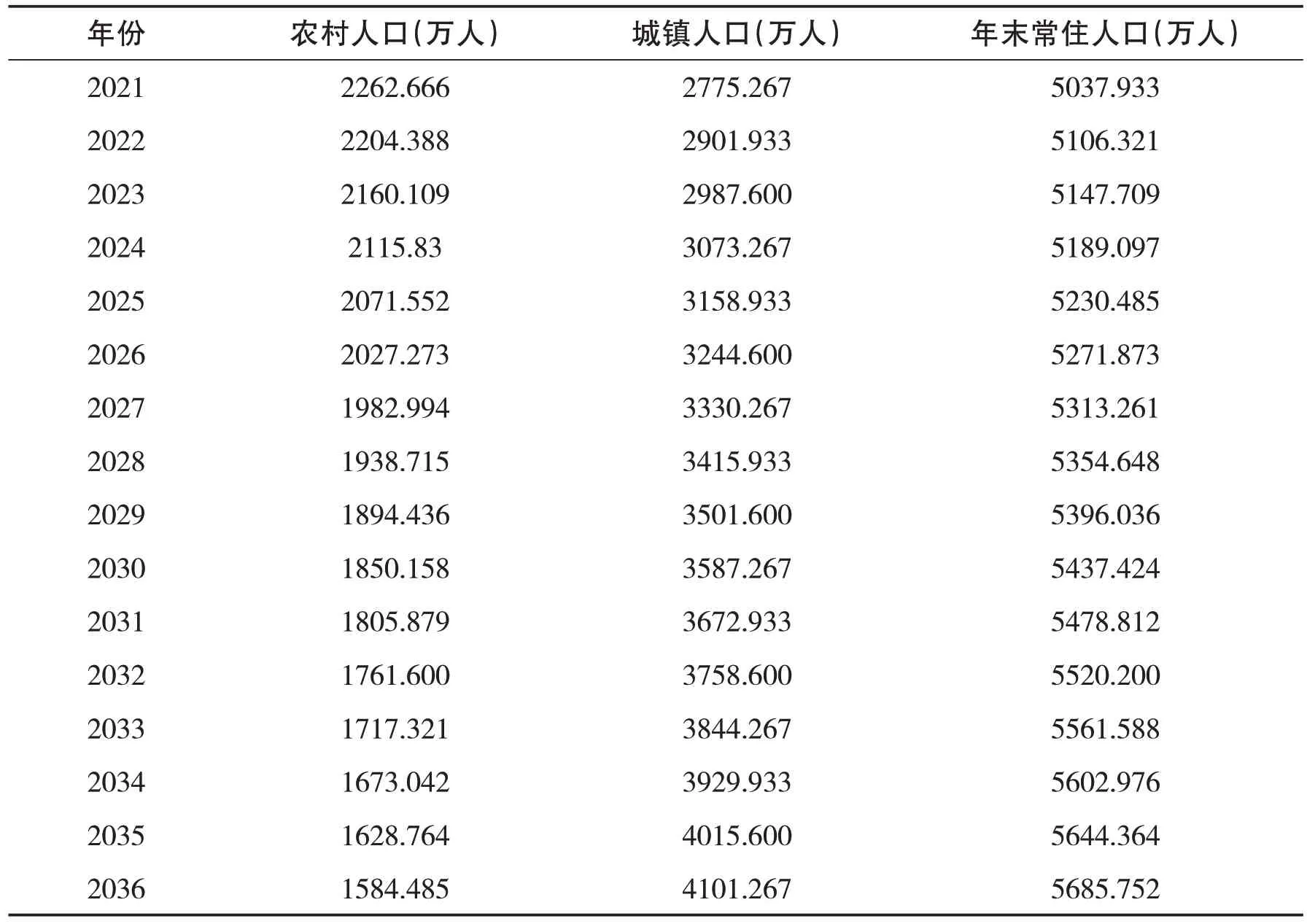
表1 广西2021—2036年人口预测结果统计表

2.2 ARIMA（p，d，q）模型求解预测广西人口

数据来源与2.1.1数据相同，这里选取的是年末常住人口数，对数据用MATLAB软件进行一次单位根检验，判定该数据序列的平稳性.这里得到的值为0.96，大于检验的临界值0.05，所以该数据序列不平稳.通过对这些不平稳数据序列进行差分处理，差分的次数用表示，对其经过差分处理之后变为平稳序列.

由图5可知，该人口数序列对其进行3阶差分后已无明显趋势，因此，我们可以认为该时间序列平稳.

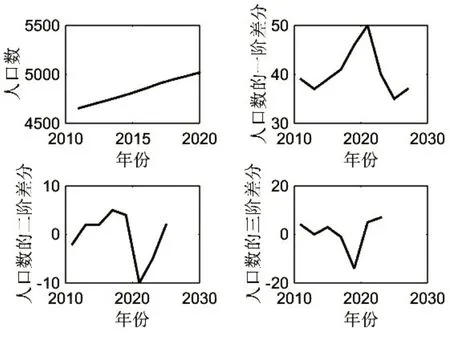
图5 2011—2020广西年末人口数的差分图

本研究对已经平稳的数据序列进行白噪声检验，判断数据序列是否是纯粹的随机序列，由于Ljung-Box检验用得相对较多，故采用此检测方法.经过检测，我们可以发现值为0.007435，小于标准值0.05，所以对数据序列进行三阶差分后的平稳序列不是随机序列，是可以开展下一步工作的.

经过前面对数据序列的差分，现在确定模型的阶数，画出序列的自相关图（ACF）和偏自相关图（PACF），具体详见图6.

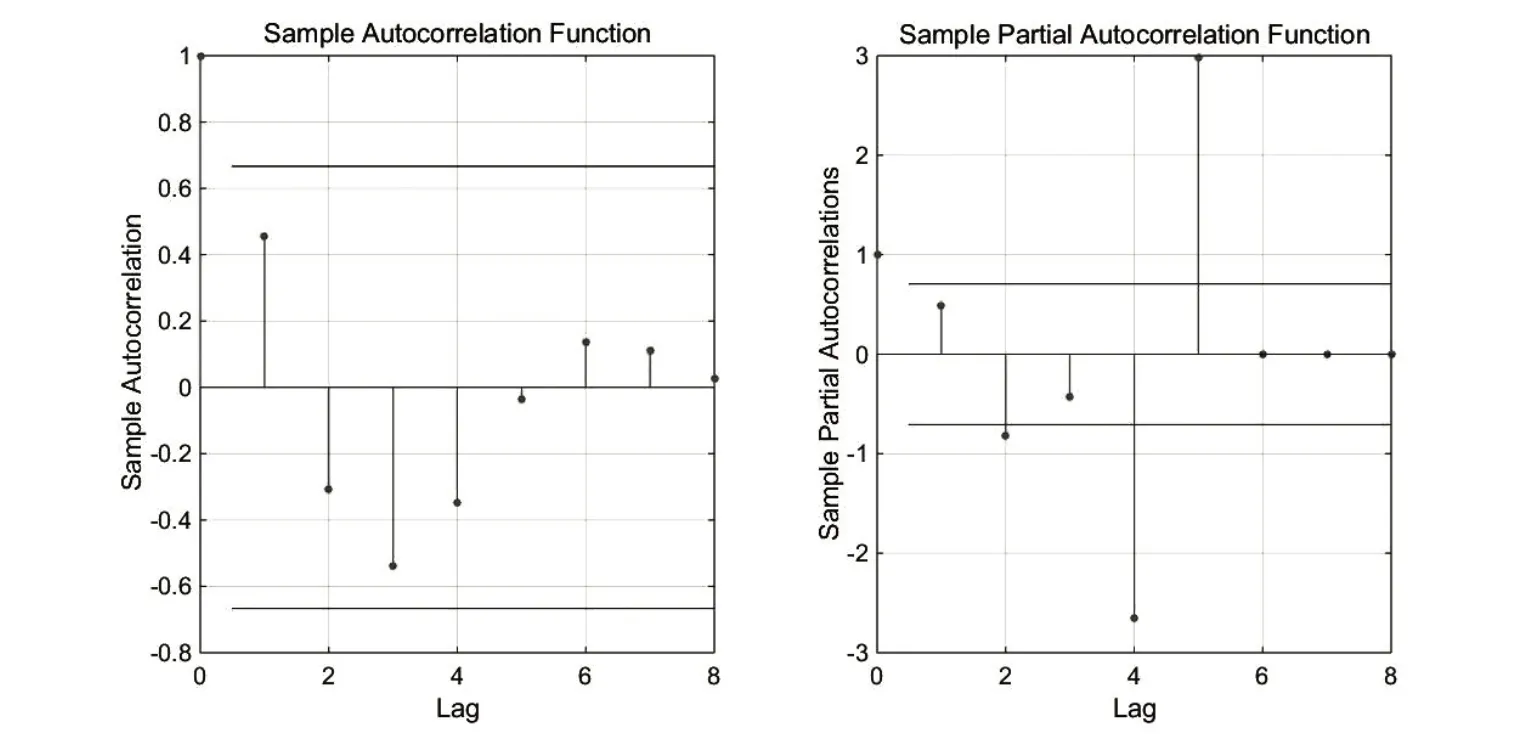
图6 自相关图和偏自相关图

由图6可知，ACF图3阶截尾，PACF图具有拖尾性，判定模型为ARIMA（0，3，3）.同时，根据MATLAB软件的运算，可以得出该模型为

用ARIMA（0，3，3）模型预测2021—2036年广西农村人口数、城镇人口数和年末人口总数，得到的预测结果如图7所示.

图7 ARIMA（p，d，q）模型预测2021—2036年广西年末常住人口

由图7可知，利用ARIMA（p，d，q）模型对2021—2036年广西农村人口数、城镇人口数和年末常住人口数进行预测，本研究发现城镇人口数和年末常住人口数总体呈上升趋势，而农村人口数则呈下降趋势，与BP神经网络模型预测的结果是一样的.但是ARIMA（p，d，q）模型受时间影响，只能对中短期的数据进行预测，对于较长时间数据的预测会出现不精准的结果.

3 结语

本研究通过对2011—2020年广西全区年末人口数量进行分析，采用BP神经网络和时间序列ARIMA（p，d，q）模型对2021—2036年的广西年末常住人口数进行了预测，发现均呈上升趋势.通过图形可知，BP神经网络对于年末常住总人口数的预测效果较好，预测每一年的年末人口数过程比ARIMA（p，d，q）模型预测过程精简，无论是从拟合度还是从变化趋势中短期预测都有很高的可信度.