基于改进蒙特卡洛法求解辐射传热问题的计算精度评价

李国军，钟佳琪，李定勇，王晓东

（1.东北大学冶金学院，辽宁沈阳 110000；2.吉利汽车自动化研究所，浙江宁波 315000）

能源动力、航空航天等领域的传热过程通常以辐射传热为主，大多数情况该类问题难于进行解析求解而多借助于数值方法进行求解，故而对该类问题的数值计算方法研究具有重要意义［1-5］.蒙特卡洛方法（Monte Carlo method，MCM）可以精确地处理光谱特性、非均匀介质、各向异性散射及复杂几何形状等复杂辐射计算问题，已经成为解决辐射传热的主要数值计算方法之一［6-9］.MCM 是一种统计模拟方法，其数值结果的精度随着抽样能束数目的增加而提高，而计算时间随着追踪能束数的增加而增加.为兼顾计算精度及计算时间，笔者提出了一种改进MCM［10］，该方法可以在只进行一次抽样情况下完成辐射换热求解，且其计算精度及计算效率高于传统MCM.随着MCM 在辐射传热数值模拟计算应用范围的不断扩展，如何定量分析和评估其计算结果的误差及精度已成为关注的焦点，建立公认的数值误差分析和精度评估方法成为MCM 主要研究内容之一.Siegel 等［11］首次用不确定度来估计MCM 计算辐射传热问题的统计误差.Planas Almazan［12］运用MCM 射线路径轨迹量化了混合网交换公式固有的统计误差.Plotnikov 和Shkarupa［13］应用直接模拟MCM 求解稀薄气体动力学问题的统计误差.阮立明等［14］利用辐射交换因子的守恒性和互易性的检验来评估MCM的计算误差，得到一种间接评价MCM计算精度的方法.Yarahmadi等［15］提出一种改进平均相对不确定评价方法，验证由于表面温度和发射率的不确定性而引起的净热流密度不确定度的新表达式.Wang等人［16-17］提出了一种直接定量评价MCM 精确度的评价方法.

为评价改进MCM 计算精度，本文拟采用改进MCM 分别对漫灰表面、参与性各项同性介质的方形及圆形封闭腔体内的辐射传热问题进行研究，建立表面和体积微元辐射热通量的误差计算模型，得出其最小误差与能束数的函数关系.采用直接定量评价方法开展基于辐射热通量的改进MCM计算误差的分析和精度评价，研究网格密度及采样能束数变化对改进MCM求解辐射传热计算精度及效率的影响.

1 改进蒙特卡洛法简介

应用区域法求解辐射换热时，当表面段和体积段的参数确定后，各段之间的辐射传递因子也可通过计算获得.若假定微元发射的全部能量到达其他各段能量的比例与该微元反射能量到达其他各段能量的比例相同，与发射能量份额及反射能量的份额无关，则采用MCM 求解辐射传递因子时，对全部微元发射的能束只需进行一次采样追踪，以确定微元段发射能量到达其他微元段的比例.当表面微元反射时，将反射能束按发射能束处理，且到达其他段的比例在之前已经确定，无需再计算，散射情况也类似处理.该思路即为改进MCM，具体求解方法如下.

1.1 微元发射能束直接到达其他微元段比例

为方便计算，将表面微元按顺序依次命名为1，2，…，Ns，体积微元安排在表面微元之后为Ns+1，Ns+2，…，Ns+Ng，其中Ng和Ns分别为体积和表面微元总数，则总微元数为Ns+Ng.则热交换场中微元i发射能束直接到达微元j比例为

式中：kUi,j（k=1，2，3，…）表示第i个微元发射的能量第k次循环到达第j个微元的能束数，Ni为第i段发射的总能束数，当k=1时表示直接到达.

1.2 微元发射能束到达其他微元段的总能束数

第i个微元发射的能量最终到达第j个微元的能量Ui,j分为直接到达被吸收的能量及经k次反射后到达被吸收的能量的累加，则

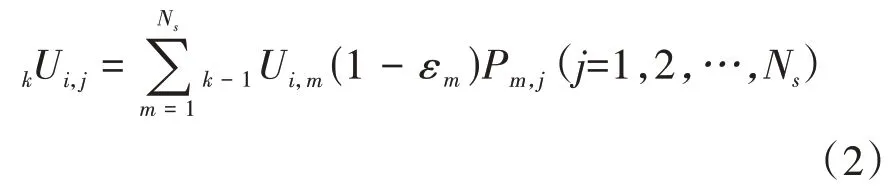
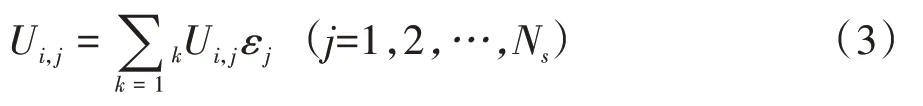
式中：Ui,j为第i微元段发射能束到达第j微元段能束总数，其中包含直接到达与反射到达情况，ε为微元段黑度.

对体积微元j=Ns+1，Ns+2，…，Ns+Ng有

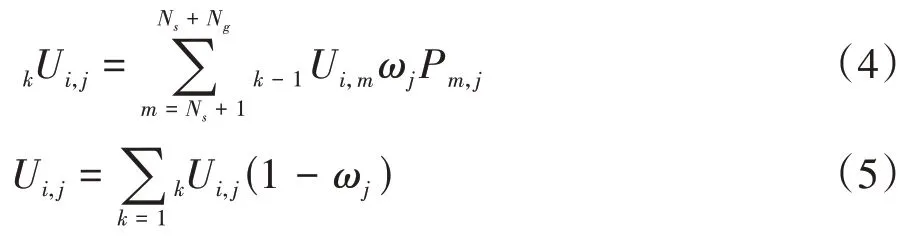
式中：ω为散射反照率，Ui,j为第i微元段发射能束到达第j微元段能束总数，其中包含直接到达与散射到达情况.

当介质为各项同性散射介质时，

反照率为

式中：κe为含粒子介质系的衰减系数，κsp为含粒子介质系的粒子的衰减系数，ω表示散射介质的散射反照率.

首先确定一个随机数R，如果R＞ω，则能束被吸收，否则被散射.

确定散射方向是MCM 研究含粒子系辐射传递的关键.本文仅计算各向同性散射，已知散射相函数的归一化条件

对于各项同性散射的散射相函数表达为

对于各项同性散射，即b=0时

1.3 计算终止条件

当微元段i发射的能束经过多次的反射或散射后剩余能量逐渐减少，当剩余能量与发射能量的比值满足式（10）时，式中ξ为无穷小量，则认为计算精度已经满足要求.

2 直接定量评价法

将辐射体系划分为M个面元和N个体积微元，则表面和体积微元净辐射热通量

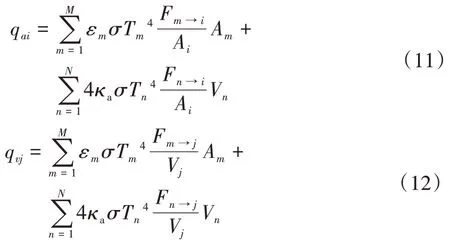
因计算过程中存在误差，则其真值可以描述为计算值与计算误差之和，即

式中：Fm→i为表面微元m对表面微元i的辐射交换因子；Fn→j为体积微元n对体积微元j的辐射交换因子；ε是表面微元i的黑度；κa是气体光学厚度；A、V分别为表面微元的面积和体积微元的体积；qai、qvj分别为表面微元i、体积微元j上的净辐射热通量；为计算值；Δqai、Δqvj为计算误差.

在等温辐射平衡状态下，净辐射通量理论上为0，则微元段吸收的辐射能量与发射的辐射能量理论上绝对相等，从而得到表面微元无因次方程为

由式（11）（13）（15），可得表面微元i的无因次净辐射热流与精确值的偏差

同理可得，体积微元j的无因次净辐射热流与精确值的偏差

则表面微元和体积微元的辐射热通量相对误差为

表面和体积微元辐射通量的相对均方根误差表示为

3 结果与讨论

3.1 网格密度对计算误差的影响

以漫灰表面、参与性各向同性介质的方形及圆形封闭腔体内的辐射传热问题为例，如图1 所示，将边长为L的方腔离散按长度方向Nx和高度方向Ny均匀划分网格；将半径为R的圆形腔体沿径向Nr及周向Nz划分为均匀网格.本节中引入光学厚度τg=并分析网格划分密度对计算误差影响.计算设定条件为：设方腔离散网格数为Nx=Ny=5，10，20，40，圆形腔体离散网格数为Nz=4，14，28，40，Nr=2.微元发射能束N=105，表面发射率ε=0.5，介质的散射反照率ω=0.5.为减小伪随机数的随机性对计算结果的影响，本文采用2 次计算结果及其平均值进行研究.

图1 算例图Fig.1 The physical model of two-dimensional cavity

由于伪随机数的随机性，不同的离散网格密度的计算结果随机误差均值表现出不同的噪声.以图2（a）（b）（c）（d）和图2（e）（f）（g）（h）所示，离散网格密度较小则误差波动明显，离散网格密度越大，结果越稳定，并且离散网格密度的增加使改进MCM 计算结果的随机性和任意性最小化到更小的程度.从图2可以看出，方形网格数取Nx=Ny=40，圆形网格数取Nz=40，Nr=2即可满足精度条件.

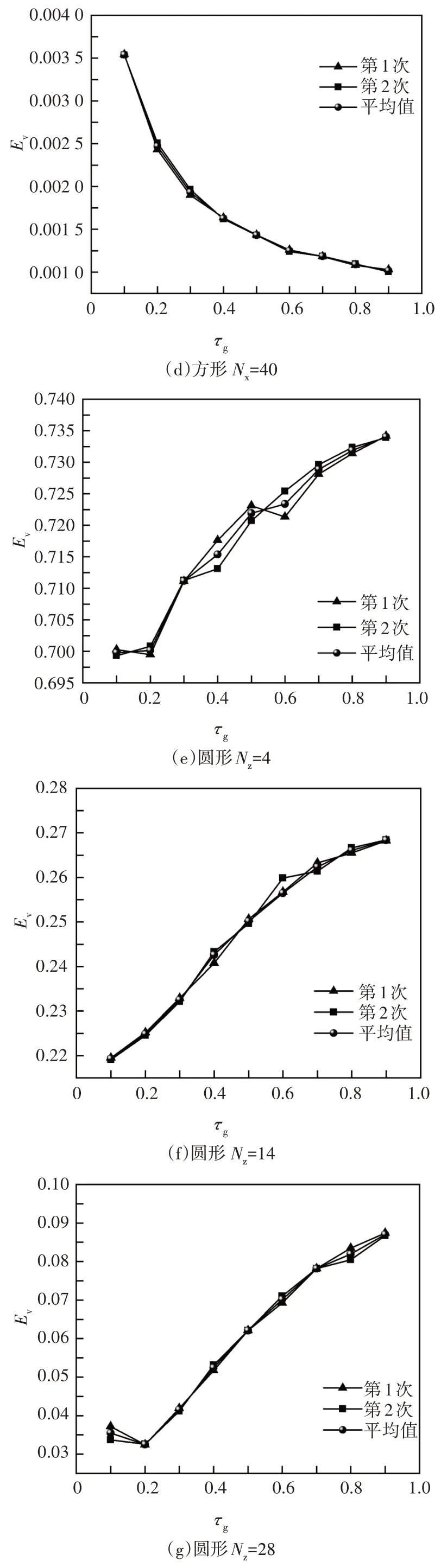
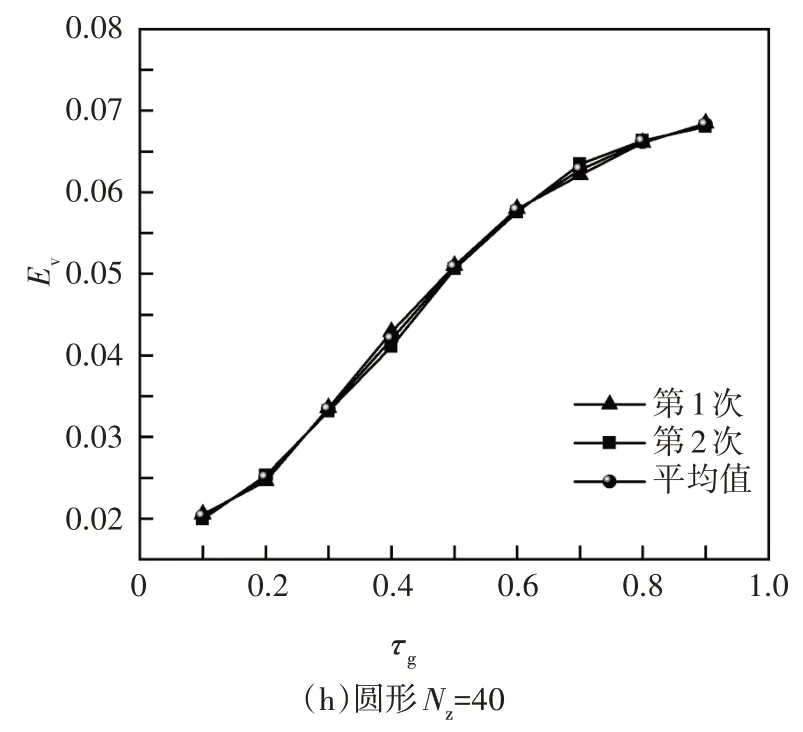
图2 不同网格密度下体积微元辐射热通量计算误差Fig.2 Calculation error of radiant heat flux of gas elements with different grid density

3.2 辐射传热量的精确值和计算值

以漫灰表面、参与性各向同性介质的方形及圆形封闭腔体内的辐射传热问题为例，将方形离散成均匀表面微元和体积微元，其中Nx=Ny=40.将圆形腔体沿径向及周向分别划分为均匀网格，即Nz=40，Nr=2.网格划分如图1所示.

当微元发射能束数N=105，表面发射率ε方=0.8，ε圆=0.5，介质的散射反照率ω=0.5，气体光学厚度分别为τg=0.000 5，τg=0.5，τg=50 时，表面微元无因次热通量计算结果分别如图3所示.

由图3 可知，光学厚度不同时，分别采用改进MCM 及MCM 计算方腔及圆形腔内表面微元无因次热通量的计算值与真实值误差较小.当τg=0.00 5时，采用改进MCM 求解得到的方腔及圆形腔的相对均方根误差Ea分别为0.002 5 及0.002 3（MCM 求解得到的方腔及圆形腔的相对均方根误差Ea分别为0.008 0 及0.003 7）；当τg=0.5 时，其改进MCM 求解的Ea分别为0.002 9 及0.0028（MCM 求解的Ea分别为0.014 1 及0.011 6）；当τg=50 时，其改进MCM 求解的Ea分别为0.003 2 及0.0031（MCM 求解的Ea分别为0.027 0及0.023 8）.由此可以看出，改进MCM对方腔及圆形腔具有相同适用性，在相同条件下其求解精度高于MCM.

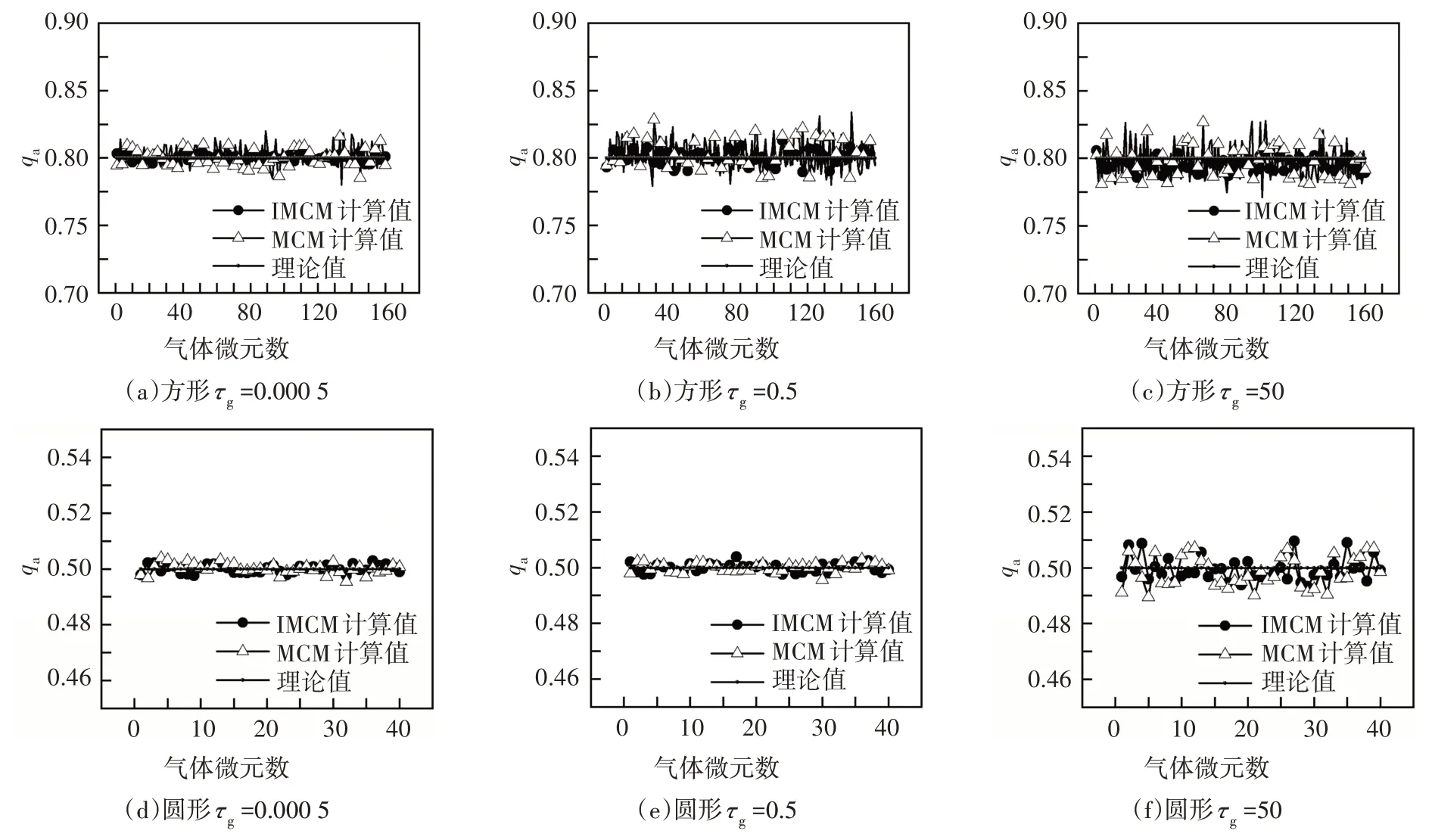
图3 表面微元吸收的辐射热通量的计算值和精度值Fig.3 Calculation and accuracy of radiative heat flux absorbed by surface elements

图4给出了气体光学厚度分别为τg=50，τg=0.5，τg=0.000 5 时方腔及圆形腔体积微元辐射热通量计算值与真实值关系.由图可知，当τg=0.000 5 时，用改进MCM 求解得到的方腔及圆形腔的相对均方根误差Ev分别为0.0013 8 及0.026 8（MCM 求解的Ev分别为0.040 3 及0.097 8）；当τg=0.5 时，方腔及圆形腔的相对均方根误差Ev分别为0.014 2及0.051 2（MCM求解的Ev分别为0.040 3 及0.120 7）；当τg=50 时，方腔及圆形腔的相对均方根误差Ev分别为0.499 7 及0.146 2（MCM求解的Ev分别为1.001 8及0.478 2）.可见，当其他条件不变时，随着光学厚度增加，MCM 及改进MCM计算结果误差有增大趋势.

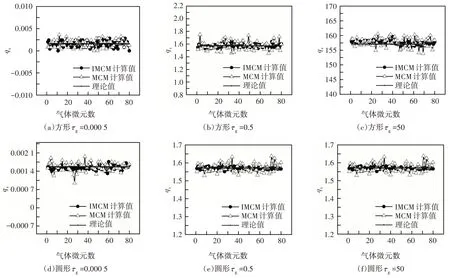
图4 体积微元吸收的辐射热通量的计算值和精度值Fig.4 Calculation and accuracy of radiative heat flux absorbed by gas elements

3.3 微元发射能束数与计算误差关系

设方形及圆形的表面发射率ε=0.5，介质的散射反照率ω=0.5，当微元发射能束数N分别为N=1 000，3 000，5 000，10 000，100 000，500 000时，求解表面和体积微元无因次热通量最小误差值.

表1 给出了Ea，min、Ev，min与微元发射能束数之间的关系.可以看出，随着微元发射能束数增加，最小误差逐渐减小.对圆形封闭腔，无因次热通量最小误差值Ea，min与微元发射能束数N的关系可拟合为如式（22）所示.

表1 Ea，min和Ev，min随N的变化Tab.1 The change of Ea，min and Ev，min with different N

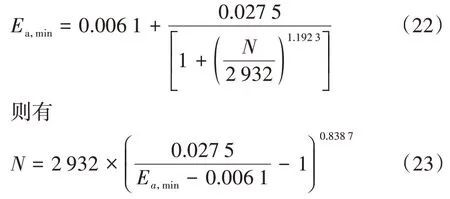
由图5 可知，计算精度随着微元能束数的增加而提高，但是当达到一定的微元能束数时，能束数继续增加对计算精度提升逐渐不明显.通常对于燃烧模拟，辐射传热计算中可接受的Ea，min误差水平要求约为0.01，所以对于用改进MCM 求解辐射传热的方形和圆形算例分别需要微元能束数N=5 000 和N=10 000 即为满足精度要求.通过式（23）可以获得不同最小误差要求情况下需要的微元能束数目.

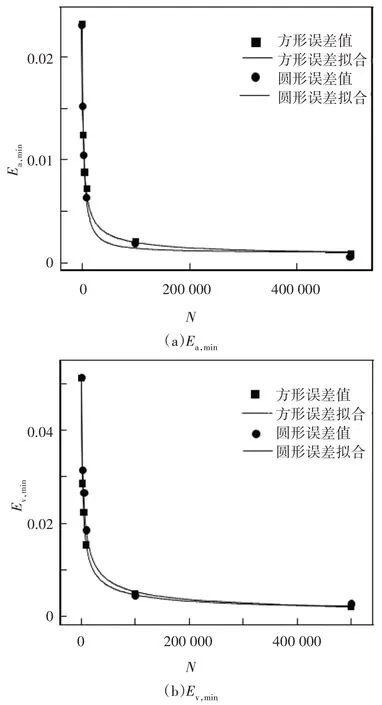
图5 Ea，min和Ev，min与N的函数关系Fig.5 The functional relationship between Ea，min，Ev，min and N

4 结论

本文阐述了基于改进MCM 进行求解辐射换热问题的思路，并引入直接定量评价方法对不同光学厚度情况下的圆形腔及方腔内参与性介质的辐射热通量计算精度进行了评价.研究结果如下：

1）改进MCM 对方腔及圆形腔内辐射问题具有适用性，在相同计算条件下，其直接评价结果明显高于采用改进MCM 进行计算的精度.如对于光学厚度为0.005 时，对方腔及圆形腔，采用改进MCM 的Ea值分别0.002 5 及0.002 3 而采用MCM 时Ea分别为0.008 0及0.003 7.

2）研究了微元发射能束数与计算误差关系，给出了能束数与Ea关系拟合式，为采用改进MCM 进行辐射换热计算提供追踪能束数选取的依据.