EHB 用无刷直流电机齿槽转矩抑制方法研究

刘金刚，郑剑云，张聪悦，傅兵，王高升，肖绍熙

（湘潭大学机械工程学院，湖南湘潭 411105）

无刷直流电机（BLDCM）具有体积小、质量轻、功率密度高、可靠性高等优点，非常适合用作电子液压制动系统（EHB）的助力电机［1-3］.然而，由于转子永磁体与定子铁心的齿槽相互作用，包括BLDCM 在内的齿槽结构永磁电机都会产生齿槽转矩［4］.齿槽转矩的存在将导致转矩脉动增加，带来振动与噪声，影响无刷直流电机的性能.

如何降低永磁电机齿槽转矩，至今都是国内外学者研究热点之一，众多学者在电机本体结构设计改进方面做了大量工作［5］，在定子侧的结构参数改进上，Wang D等人［6］在保证槽口宽度相同前提下，采用非均匀齿冠宽度的方法，并通过解析分析确定了齿冠宽度比，大大降低齿槽转矩；黄守道等人［7］根据齿槽转矩解析表达式，分析了单个槽对齿槽转矩增加规律的影响，提出通过槽口偏移来减弱齿槽转矩的方法；Wang K 等人［8］利用定子齿的偏心结构来减小齿槽转矩，并在一台外转子PMSM 上验证了所提方法的有效性.在转子侧的结构参数改进上，安治国等人［9］研究了转子辅助槽添加位置、开槽深度和宽度等参数对齿槽转矩和漏磁的作用情况，获得最佳开槽结构参数；Zhao J 等人［10］对永磁体边缘的结构参数进行了研究，通过改变参数减少了转子端部效应的影响，抑制了齿槽转矩；李松生等人［11］进行了转子永磁体对齐安装和错位安装的对比，发现分段斜极安装可以大幅降低齿槽转矩.上述提出的结构改进方法能降低电机齿槽转矩，但鲜有同时兼顾永磁体形状参数和电枢参数改进的方法，也很少综合考虑齿槽转矩和电机其他基本性能.

本文通过对齿槽转矩的表达式进行推导和分析，发现其数值由基本结构参数以及傅里叶分解系数Br（nz/2p）和Gn所决定，以此为依据，推导了傅里叶分解系数和结构参数的关系式.再利用有限元方法分别研究了BLDCM 偏心距改变、极弧系数变更和添加辅助槽三种情况下齿槽转矩、气隙磁密和反电动势的变化情况.结果表明，对结构参数进行合理地改进，可以在保持电机性能基本不变的情况下抑制齿槽转矩.

1 结构参数与齿槽转矩的关系分析

1.1 齿槽转矩分析

由于齿槽结构的影响，当转子永磁体处于不同位置时，磁路中的磁阻会发生变化，从而引起磁场能量变化，导致齿槽转矩的产生.因此，将齿槽转矩定义为磁场能量W相对于位置角a的函数［12］，即：

为便于分析，做以下假设：定子铁心磁导率为无穷大；不同永磁体之间结构及磁性能处于理想状态，无加工制造误差，磁导率与空气相同；硅钢片的叠装系数为1.因此，永磁电机磁场中存储的磁能可近似为气隙与永磁体磁能之和［13］，可表示为：

式中，B为气隙磁通密度；μ0为磁导率；V为气隙体积.其中气隙磁密沿电枢表面分布可表示为：

式中，Br（θ）为永磁体剩磁沿圆周方向的分布；hm(θ)、δ(θ，α)分别为沿圆周、磁化方向的气隙长度.

将式（2）和式（3）代入式（1），进行傅里叶分解展开并求导，可得齿槽转矩表达式如下：

式中，R1、R2分别为转子外径和定子内径；Z为槽数；L为铁心长度；Gn和Br（nz/2p）为傅里叶分解所对应n次和nz/2p次谐波系数；p0为极对数.

由式（4）可知，齿槽转矩由基本结构参数、分解系数Br（nz/2p）和Gn决定.电机设计完成后，R1、R2、Z、L等基本结构参数已经确定，因此抑制齿槽转矩可从分解系数Br（nz/2p）和Gn上着手.Br（nz/2p）的数值主要由永磁体偏心距、极弧系数等决定，而Gn的幅值主要与槽口宽度和辅助槽添加等有关.

1.2 偏心距与齿槽转矩的关系分析

BLDCM 转子采用面包形表贴式结构，永磁体形状如图1 所示，为方便分析将面包形永磁体分为a、b两部分，b部分的圆心与转子圆心重合.

永磁磁体a、b 两部分充磁厚度之和为h′m（θ），可以表示为：

式中，Ra、Rb分别表示a、b 部分的半径；Δh表示偏心距，是永磁体外部弧面圆心Oa与转子中心Ob的距离；lδ表示永磁体底部平面与转子中心Ob的距离.

面包形永磁体偏心时，气隙长度随之产生变化，但实际气隙长度与永磁体的充磁方向厚度之和保持不变，因此径向气隙磁密B′(θ，α)可以表示为：

进一步可以得到Br′(θ)，其表达式为：

式中，hmax表示永磁体最大充磁厚度.将hm′(θ)的表达式（5）代入式（7），得到Br′2(θ)的表达式：

永磁体偏心设计的目的是使得气隙不均匀，从而获取预想的气隙磁通密度分布，其程度可通过偏心距Δh的数值大小来体现.以Δh为变量时，不考虑极弧系数km的影响，将km设置为初始值0.86，则Br′2(θ)可转化为关于偏心距Δh和位置θ的函数，即：

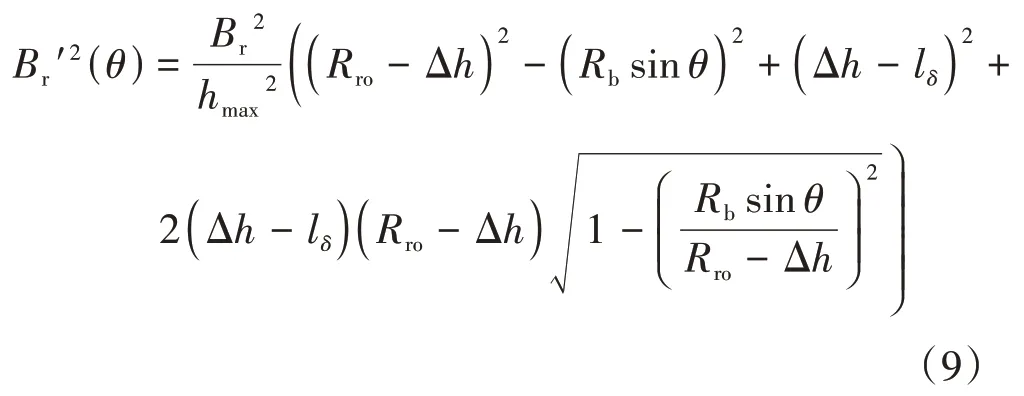
经过推导，得到Br′2(θ)在分解区间［-πkm/2p，πkm/2p］上的傅里叶各次分解系数Bm：

由式（10）和式（4）可知，随着Δh的增大，Br′2(θ)的傅里叶分解系数Bm降低，进而减小齿槽转矩.

1.3 极弧系数与齿槽转矩的关系分析

永磁体极弧的宽度bm和极距τ 之比被称之为极弧系数km，其表达式为：

以极弧系数km为改进变量，研究其对齿槽转矩Tc的影响时，不考虑偏心情况，设置Δh取值为零，则Br′2(θ)可以表示为关于位置角θ和极弧系数km的函数，其表达式为：

Br′2(θ)在区间［-πkm/2p，πkm/2p］上的傅里叶各次分解系数Bm的函数，可以转换为与极弧系数km相关的函数，其表达式如下：

由式（13）和式（4）可知，调整极弧系数km可以使得分解系数Bm取较小值，从而可以对齿槽转矩进行抑制.

1.4 辅助槽与齿槽转矩的关系分析

电枢是电机实现能量转化中起到关键枢纽作用的部分，在BLDCM 中电枢指的是定子部分，其设计的关键在于槽形参数选取.槽形参数的设计会影响在定子内表面的分布，改变其傅里叶展开系数Gn的取值，进而改变齿槽转矩Tc的大小.

在分析电枢参数对Tc影响情况时，可忽略转子部分参数的作用，将简化为.其中，槽口宽度β（以弧度制表示）是重要的槽形参数之一，其数值会直接改变的分解区间，槽口宽度与积分区间的关系如图2所示.

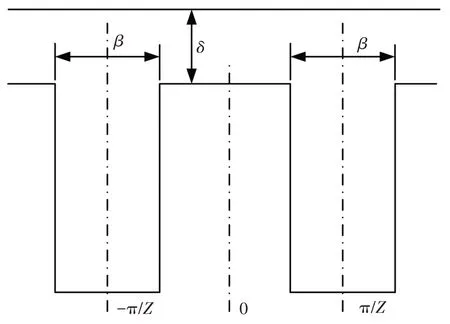
图2 槽口宽度与积分区间关系示意图Fig.2 The relationship between cogging notch width and integral interval

式中：β为用弧度表示的槽口宽度，β≈；b0表示定子槽口宽度.

由式（14）可知，适当地选取槽口宽度，可以改变Gn，从而抑制齿槽转矩.然而，槽口过小时可能会引起漏磁，过大时容易造成定子齿部饱和，因此槽口取值范围要合理选取.

槽口宽度β的改变常与辅助槽添加配合使用，添加辅助槽等于增加BLDCM 开槽数目，更改极槽配比，使得新添加的槽与原先的齿槽转矩进行抵消，进而对其进行削弱.矩形的定子辅助槽均匀添加在齿顶上，宽度为β，与原槽口的宽度一致，具有一定开槽深度，辅助槽添加示意图如图3所示.

图3 辅助槽添加示意图Fig.3 Schematic diagram of adding auxiliary slot

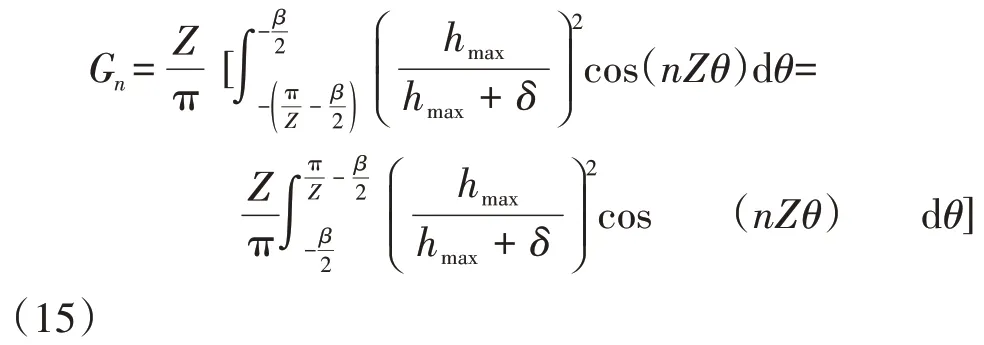
由式（15）和式（4）可知，适当地选取辅助槽，可以改变傅里叶分解系数Gn，从而抑制齿槽转矩.

2 无刷直流电机有限元建模

理论分析了偏心距、极弧系数和辅助槽与齿槽转矩傅里叶分解系数之间的关系，发现改变三者的数值大小可以减小齿槽转矩.但是，这是基于假设推导得到的，而实际情况十分复杂，需要仿真来进一步分析.有限元方法可以全面考虑电机漏磁、磁饱和等复杂情况，相较于理论分析更为精确.因此，为准确分析齿槽转矩敏感结构参数对齿槽转矩和电机其他性能的影响，本文基于电机结构参数，如表1 所示，搭建了无刷直流电机三维模型，如图4 所示.并使用Ansoft Maxwell 软件建立了8 极12 槽BLDCM 的有限元分析模型，对其进行材料定义、边界设置、激励添加和网格剖分，建立的有限元模型如图5所示.

表1 BLDCM 主要结构参数Tab.1 Main structural parameters of BLDCM

图4 无刷直流电机三维模型Fig.4 Three dimensional model of Brushless DC motor

图5 无刷直流电机有限元模型Fig.5 Finite element model of Brushless DC motor

在有限元求解设置中，将电机设置为恒转速工况，绕组电流设置为零，以永磁体磁场为激励，对该电机进行有限元仿真计算.

3 仿真结果分析

3.1 偏心距改变对齿槽转矩的影响

为获取能有效抑制齿槽转矩的偏心距数值，在其取值范围0.00～9.00 mm 内，以1.00 mm 为步长进行仿真分析.得到齿槽转矩峰值Tcmax随偏心距Δh的变化情况，如图6所示.

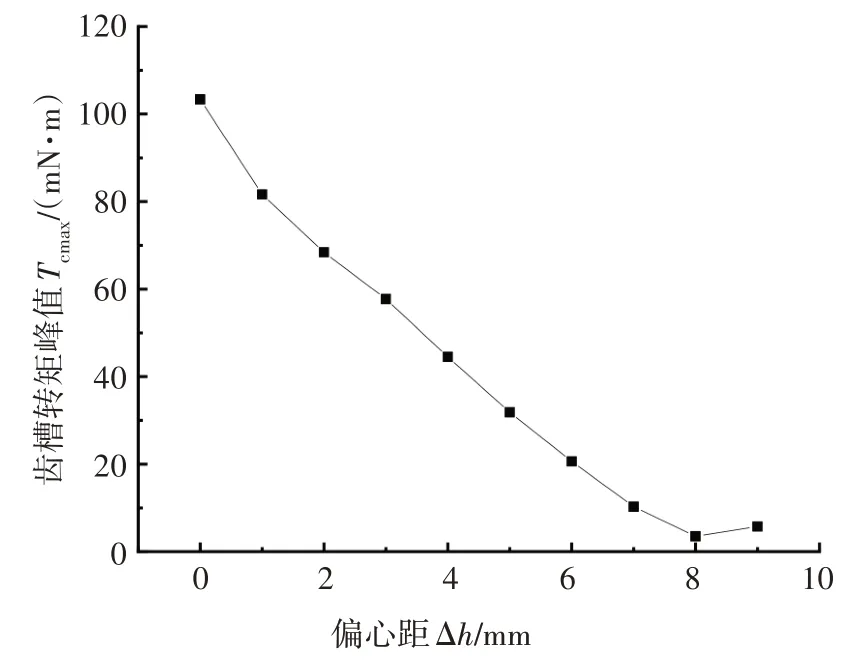
图6 偏心距为0～9 mm时的齿槽转矩变化情况Fig.6 Variation of peak cogging torque when eccentricity is 0～9 mm

由图6 可知，随偏心距Δh的增加齿槽转矩峰值Tcmax呈现先减小后增大的趋势，这与理论分析中的Bm变化趋势相一致.同时，发现当偏心距Δh取值为8.00 mm 时，齿槽转矩峰值取到最小值3.51 mN·m；当Δh取值为9.00 mm时次之，峰值为5.74 mN·m.

为更准确地分析偏心距改变对齿槽转矩的影响，对上述取值进行再次细分后仿真.在有限元分析中，偏心距取值以8.00 mm 为中心，在7.00～9.00 mm范围内，以0.10 mm 为步长进行仿真，Tcmax随Δh变化情况，如图7 所示.由图7 可知，Δh=7.9 mm 时齿槽转矩出现最小值，峰值为3.48 mN·m.

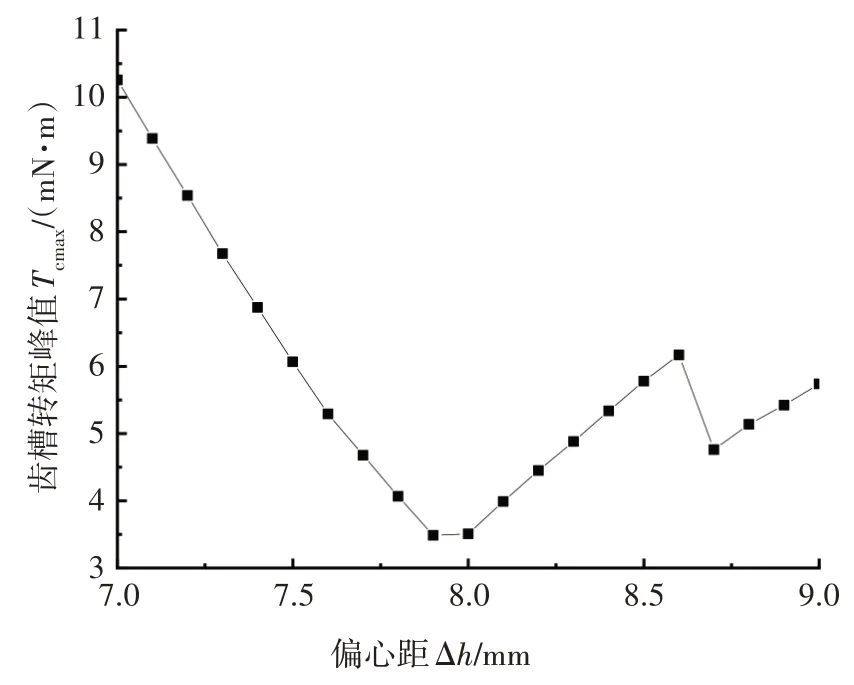
图7 齿槽转矩随偏心距的变化情况Fig.7 Variation of peak cogging torque with eccentricity

偏心距Δh改变前后齿槽转矩Tc的曲线波形对比、气隙磁密对比和反电动势曲线的波形对比分别如图8～10 所示.由图8 可知，改变前永磁体不偏心，即Δh=0 mm，齿槽转矩峰值Tcmax为103.91 mN·m；改变后，Δh为7.90 mm，Tcmax减少为3.48 mN·m，相比改变前降低了96.65%.由图9 可知，改变前，气隙磁密Bδ的峰值为0.88 T；改变后，由于永磁体最大厚度没有改变，所以气隙磁密Bδ的峰值基本不变，但是由于Δh的增加，导致曲线波形变尖.由图10 可知，改变前，反电动势E的峰值为5.27 V；改变后，波形平顶宽度变窄，反电动势E的峰值减小为4.71 V，相较于改变前降低了10.66%.

图8 偏心距改变前后齿槽转矩波形对比图Fig.8 Comparison of cogging torque waveforms before and after eccentricity change

图9 偏心距改变前后的气隙磁密波形对比Fig.9 Comparison of air gap flux density waveforms before and after eccentricity change

图10 偏心距改变前后的反电动势对比Fig.10 Comparison of back EMF before and after eccentricity change

3.2 极弧系数变更对齿槽转矩的影响

在极弧系数取值范围0～1 内，以0.1 为步长进行仿真，得到齿槽转矩峰值Tcmax随极弧系数km变化情况，如图11所示.

图11 极弧系数为0～1时齿槽转矩峰值变化情况Fig.11 Variation of peak cogging torque when pole arc coefficient is 0～1

由图11 可知，Tcmax随km变化而波动，km取值为0.40 时，Tcmax出现最小值为10.84 mN·m；km取值为0.70时次之，峰值为46.40 mN·m.为更准确地分析极弧系数变更对齿槽转矩的影响，对上述取值再次细分后仿真.在有限元仿真分析中，极弧系数取值以0.70为中心，在0.60～0.80范围内，以0.01为步长进行仿真，得到齿槽转矩峰值Tcmax随极弧系数km的变化情况，如图12所示.从图12可以看出，当时齿槽转矩出现最小值，峰值为9.89 mN·m.李辉等人［14］观察到齿槽转矩峰值与极弧系数之间有相似的趋势.

图12 极弧系数为0.6～0.8时齿槽转矩峰值变化情况Fig.12 Variation of peak cogging torque when pole arc coefficient is 0.6～0.8

极弧系数km变更前后齿槽转矩Tc的曲线波形对比、气隙磁密波形对比和反电动势曲线分别如图13～15所示.由图13可知，极弧系数变更前，齿槽转矩峰值Tcmax为103.91 mN·m；变更后，Tcmax减小到9.89 mN·m，相比于变更前降低了90.47%，齿槽转矩峰值得到了明显抑制.由图14 可知，变更前，气隙磁密Bδ的峰值为0.88 T；变更后，由于永磁体最大厚度不变，所以气隙磁密的峰值基本不变，但极弧系数的减小会导致曲线顶部的宽度略微变窄.由图15 可知，变更前，反电动势E的峰值为5.27 V；变更后，反电动势E的峰值降低了0.76%，变为5.23 V.

图13 极弧系数变更前后齿槽转矩波形对比Fig.13 Comparison of cogging torque waveform before and after pole arc coefficient change

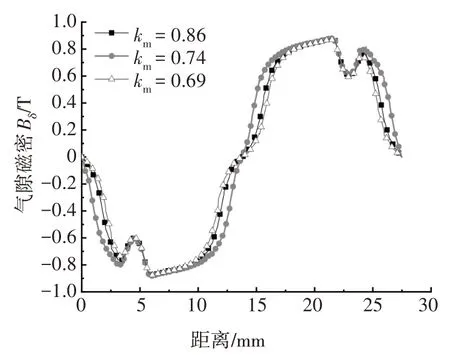
图14 极弧系数变更前后气隙磁密波形对比Fig.14 Comparison of air gap flux density waveforms before and after pole arc coefficient change

图15 极弧系数变更前后反电动势对比Fig.15 Comparison of back EMF before and after pole arc coefficient change

3.3 添加辅助槽对齿槽转矩的影响

在齿槽槽口取值范围0～5 mm 内进行仿真分析，得到了齿槽转矩峰值Tcmax随齿槽槽口宽度b0的变化情况，如图16所示.

图16 齿槽转矩峰值随槽口宽度变化情况Fig.16 Variation of peak cogging torque with the notch width

由于b0的取值受到限制，在现有范围内并没有出现最佳的取值，可以通过添加辅助槽等手段进一步对Gn进行抑制，进而减少齿槽转矩.但是，添加辅助槽后定子铁心的结构发生变化，磁导率随之改变，从而改变齿槽转矩，而不同形状辅助槽形产生的影响也会不同，因此需要对辅助槽的形状进行分析.本文针对矩形、三角形和椭圆形3 种不同形状的定子辅助槽进行分析，不同槽形比较时，将槽宽和槽深设置为不变量，以便比较形状对齿槽转矩的影响，添加不同形状辅助槽时齿槽转矩Tc的曲线波形对比、气隙磁密对比和反电动势曲线分别如图17～19所示.

图17 添加辅助槽前后齿槽转矩波形对比Fig.17 Comparison of cogging torque waveform before and after adding auxiliary slot

由图17 可知，添加的辅助槽形状为矩形时，齿槽转矩峰值Tcmax为23.10 mN·m；为三角形辅助槽时，Tcmax增大为29.59 mN·m，相较于矩形辅助槽增加了28.10%；为椭圆形辅助槽时，Tcmax降低到13.78 mN·m，相较于矩形辅助槽降低了40.35%，因此椭圆形辅助槽对齿槽转矩的削弱效果最佳.由图18 可知，添加辅助槽前，气隙磁密Bδ的曲线波形由于受到原槽口作用，顶部存在1 处凹陷；而添加辅助槽后，凹陷数量增加至3 个，相比于椭圆形辅助槽，添加矩形辅助槽和三角形辅助槽时气隙磁密波形会变得更尖.由图19 可知，添加辅助槽前，反电动势E的峰值为5.27 V；而添加不同形状辅助槽后，对应的反电动势E的峰值也有着不同程度地降低，其中添加椭圆形辅助槽时变化最小，其反电动势E的峰值为4.95 V，相较于开槽之前仅降低了6.07%.

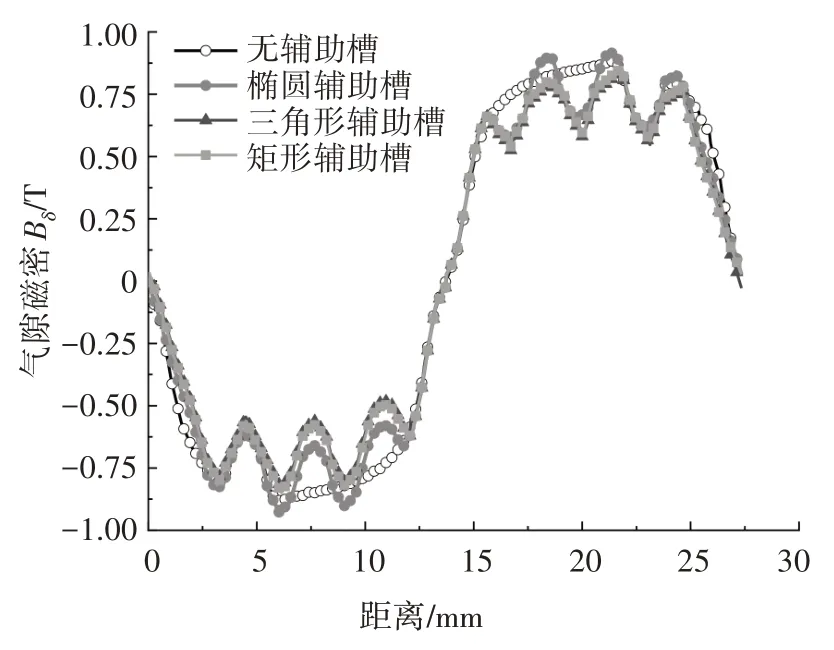
图18 添加辅助槽前后气隙磁密波形对比Fig.18 Comparison of air gap flux density waveforms before and after adding elliptical auxiliary slot

图19 添加辅助槽前后反电动势曲线对比Fig.19 Comparison of back EMF curves before and after adding elliptical auxiliary slot

4 结论

本文以EHB 用无刷直流电机为研究对象，通过对齿槽转矩的表达式进行推导和分析，发现其数值由基本结构参数以及傅里叶分解系数Br（nz/2p）和Gn所决定，以此为依据，推导了结构参数与傅里叶分解系数的关系式.并分别研究了偏心距改变、极弧系数变更和添加辅助槽对齿槽转矩和电机其他性能的影响，得到了以下结论.

1）当偏心距、极弧系数和辅助槽形状分别为7.90 mm、0.74、椭圆形时，对应的齿槽转矩峰值分别为3.48 mN·m、9.89 mN·m、13.78 mN·m，相比于改变前分别降低96.65%、90.48%、86.74%，齿槽转矩都得到了明显抑制.

2）偏心距改变、极弧系数变更和添加辅助槽会增加气隙磁密波形的凹陷数量，也会使反电动势曲线变窄，说明其对电机性能产生了一定的影响，相较而言，添加椭圆形辅助槽的影响最小.