基于混合势函数的直流微电网群稳定性分析

王玉梅，张子寒，王 浩

(河南理工大学 电气工程与自动化学院，河南 焦作 454003)

随着分布式发电与储能技术的发展，越来越多的微电网被投入使用，微电网之间互联成群已成为必然趋势。微网群可分为交流微电网群、直流微电网群和交直流混合微网群[1]。其中直流微电网群可更高效地接纳风光分布式电源、储能以及电动汽车等直流用电负荷[2]。子微网直流母线电压稳定是保证直流微电网群稳定运行的关键。光照降低以及切子微网或切大容量负载等大扰动引起母线电压波动，导致子微网进入不稳定的工作状态，影响直流微电网群稳定运行。针对此类问题，通常采用大信号稳定性分析方法，例如相平面法[3]、李雅普诺夫法[4]和混合势函数法[5]。相平面法虽然能够比较直观地判断稳定性，但无法得出系统中各个参数与稳定性之间的解析关系式。李雅普诺夫法虽然能给出解析式，但在非线性系统中会遭遇到无法建模的情况[6]，具有一定的局限性。混合势函数法是对李雅普诺夫法进行改进后的一种方法，其在非线性系统中也能给出解析式。文献[7～10]根据混合势函数对含多个恒功率负载和含多电源的直流微电网进行稳定性分析，并得到单个直流微电网的稳定性判据式。文献[11]提出适用于多直流微电网群柔性互联系统的功率协调控制策略，可提高能源利用率，但其未对直流微电网群的稳定性分析进行研究。文献[12]对交流微网群和直流微电网群进行稳定性分析，但未对直流微电网群大扰动进行分析。为此，本文通过混合势函数对直流微电网群进行大信号稳定性分析：首先，确定直流微电网群结构类型，根据DC-DC级联特性以及各子微网变换器控制方法，得到出直流微电网群等效电路；然后，根据该等效电路建立混合势函数等效模型，推导出直流微电网群大信号稳定性判据式并进行稳定性分析。

1 直流微电网群结构

1.1 直流微电网群接线结构

为有效隔离局部故障，提高直流(Direct Current，DC)微电网群供电可靠性，实现不同电压等级之间功率的双向流动，本文采用隔离型DC-DC变换器来实现微网群分段式多母线互联[11，13-14]。该微网群中两个子微网由恒功率控制的双向DC-DC变换器互联组成[15-16]，其中微网1并网运行，微网2与微网1并联。具体的结构形式如图1所示。

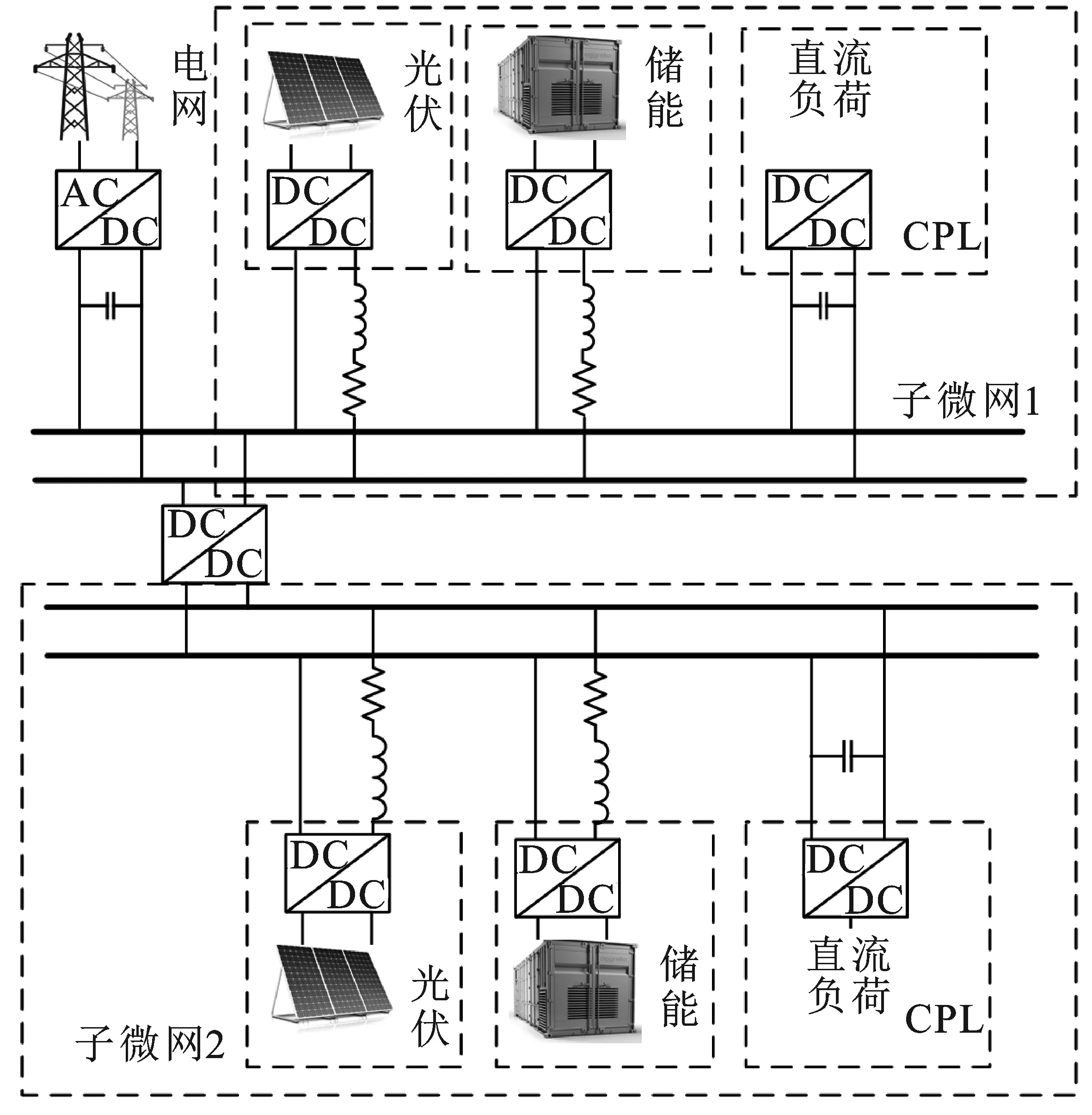
图1 直流微电网群结构Figure 1. DC microgrid group structure

由图1可以看出，子微网由光伏单元、储能系统(Energy Storage System，ESS)和恒功率负载(Constant Power Load，CPL)组成，其中子微网1由电压源换流器(Voltage Source Convertor，VSC)连接配电网[17]。

1.2 直流微电网群等效电路图

微网1与微网2连接的DC-DC变换器采用恒功率控制策略[11]，其功率守恒网络框图如图2所示。

图2 DC-DC变换器功率守恒网络框图Figure 2. Block diagram of DC-DC converter power conservation network

图2中，iin、vin为子微网提供的电流电压；iout、vout为子微网所接受到的电流电压。图2对应的数学模型如式(1)所示。

iin×vin=iout×vout

(1)

其DC-DC等效电路图如图3所示。

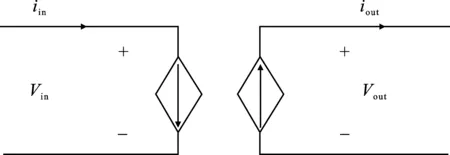
图3 DC-DC变换器大信号等效电路图Figure 3. Circuit diagram of DC-DC converter large signal equivalent

图3中，DC-DC变换器的输入、输出端口可看作电流源。由于采用恒功率控制，故两个电流源都是恒功率控制的受控电流源。通过设置变换器参考功率PDC即可改变变换器间传输的功率。

根据图1，子微网1处于并网状态，VSC采用限制功率模式，可等效为理想电压源UV1串联上一个电阻R1和电感L1的形式[17]。子微网1的ESS并网下充电，可等效成一个受控电流源，功率恒为PE。子微网2与微网1并联，ESS采用下垂控制[18]，等效为理想电压源UE2串联上一个电阻R2和电感L2。光伏单元在MPPT下工作时，等效为负的CPL，故光伏单元与正的CPL可等效为一个PCPL，用受控电流源表示[19-22]。PCPL输入侧的电容与母线上并联的其他电容统一用一个集成电容C来表示。结合图3可得到直流微电网群的等效电路图，如图4所示。

图4 并网直流微电网群等效电路图Figure 4. Equivalent circuit diagram of grid-connected DC microgrid group

图4中，iV1、iE1、iDC1、iCPL1分别为子微网1的VSC输出电流、ESS吸收电流、DC-DC变换器输入电流以及CPL两端电流；uDC1为子微网1的母线两端电压；iE2、iDC2、iCPL2分别为子微网2的ESS输出电流、DC-DC变换器输出电流、CPL两端电流；PCPL1为子微网1的CPL；PCPL2为子微网2的CPL。

2 混合势函数理论

混合势函数理论是改进的李雅普诺夫函数，适合对非线性电路进行稳定性分析。根据非线性电路中电感、电阻以及储能元件进行构建，可将混合势函数模型P定义为[5]

(2)

式中，i1,…,ir为通过非线性电路中电感的电流；Ur+1,…,Ur+s为电容两端的电压；式(1)右端的左侧为所有非储能元件的电流势函数；式(2)右端的右侧为所有电容的能量和。需通过式(3)检验混合势函数模型P的正确性。

(3)

为应用稳定性定理，将混合势函数表示为以下标准形式

P(i,U)=-Ai+BU+Di,U

(4)

式中，-A(i)为非线性电路中非储能元件的电流势函数；B(U)为电路中非储能元件的电压势函数；D(i,U)为电容和其他非储能元件的电压电流乘积[22]。

本文将用到混合势函数理论的第三条定理，为方便下文使用，现对该定理进行重述。

定义Aii(i)=∂A2/∂i2,Bvv(v)=∂B2/∂v2，设μ1为L-1Aii(i)L-1的最小特征值，设μ2为C-1Bvv(v)C-1的最小特征值，L和C分别为非线性电路中电感、电容的对角矩阵。

若电路中i、v均满足式(4)，且当|i|+|v|→∞时，满足式(5)。

μ1+μ2>0

(5)

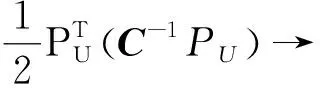
(6)

则当t→∞时，式(3)的所有解都将趋于稳态平衡点，即无论电路中电流电压如何变化，最终整个系统都会到达稳定状态。

3 直流微电网群稳定性分析

3.1 混合势函数模型建立

3.1.1 子微网1混合势函数模型P1(i,U)

所有非储能元件的电流势函数由VSC等效电压UV1、内阻R1以及恒功率负载PE、PDC1、PCPL1的电流势函数构成。其中，恒功率负载PE、PDC1、PCPL1无法用电流势函数表示，需转化成电压势函数来表示。

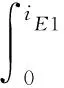
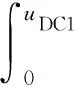
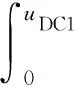
(7)

子微网1各变换器集成等效电容C1的能量为

-uDC1iV1+PE+PDC1+PCPL1

(8)

子微网1混合势函数模型为

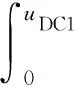
UV1iV1-uDC1iV1

(9)

将式(9)代入式(3)验证可得

(10)

结果满足式(3)，故式(9)是子微网1的混合势函数模型。

3.1.2 子微网2混合势函数模型P2(i,U)

子微网2并未接配电网，所有非储能元件的电流势函数由储能提供的电压UE2、内阻R2以及恒功率负载PDC2、PCPL2电流势函数构成。PDC2、PCPL2转化成电压势函数来表示。

(11)

子微网2各变换器集成等效电容电容C2的能量为

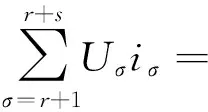
uDC2iE2-PDC2+PCPL2

(12)

子微网2混合势函数模型为

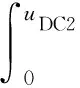
(13)

将式(14)代入式(3)验证可得

(14)

结果满足式(3)，故式(14)是子微网2的混合势函数模型。

3.2 混合势函数稳定性分析

3.2.1 子微网1稳定性判据

子微网1混合势函数模型P1可改写为

(15)

应用混合势函数理论的第3条定理可得

(16)

将式(16)代入式(5)和式(6)得到子微网1稳定性判据，如式(17)所示。

(17)

3.2.2 子微网2稳定性判据

子微网2混合势函数模型P2可改写为

(18)

应用混合势函数理论的第3条定理可得

(19)

将式(19)代入式(5)和式(6)，得到子微网2稳定性判据，如式(20)所示。

(20)

根据式(7)所示的DC-DC变换器功率守恒性质，结合微网1微网2稳定性判据式(19)、式(20)，可得直流微电网群稳定性判据为式(21)。

(21)

在直流微电网群中，光伏单元在最大功点跟踪(Maximum Power Point Tracking,MPPT)控制下等效为负的恒功率负载CPL，与恒功率的负载共同作用，等效为一个恒功率负载。地区光照降低或者大容量负载投入等大扰动都会导致PCPL变化，因此式(21)右边可表示为

(22)

当直流微电网群中的CPL发生阶跃变化，但变化后仍然符合判据式(21)时，则直流微电网群可通过DC-DC变换器设置合适的参考功率PDC，调节两个子微网之间的能量平衡，使直流微电网群保持大信号稳定；反之，则没有合适的参考功率PDC使直流微电网群保持大信号稳定。

4 仿真验证

直流微网群接线示意图如图5所示，图5中的基本参数如表1所示。

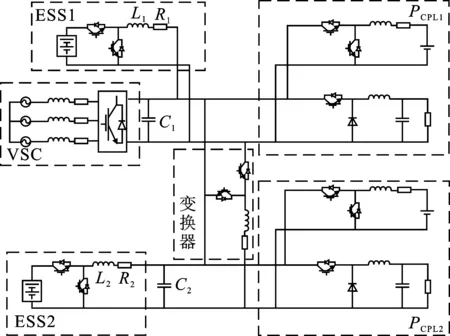
图5 直流微电网群仿真模型Figure 5. Simulation model of DC microgrid group

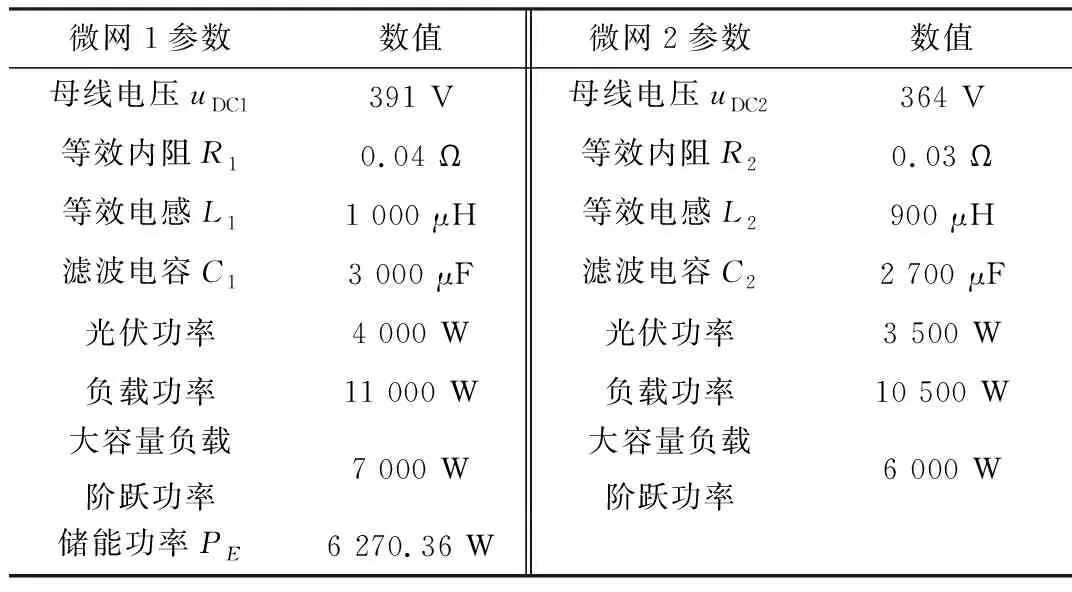
表1 直流微电网群系统基本参数

根据表1中的参数对直流微网群大扰动实际情况进行讨论。在白天，子微网大容量负载分别投入或同时投入；在夜晚，直流微网群光伏单元光照降低，光伏输出功率跌至0。如表2所示为微网群大扰动变化参数。

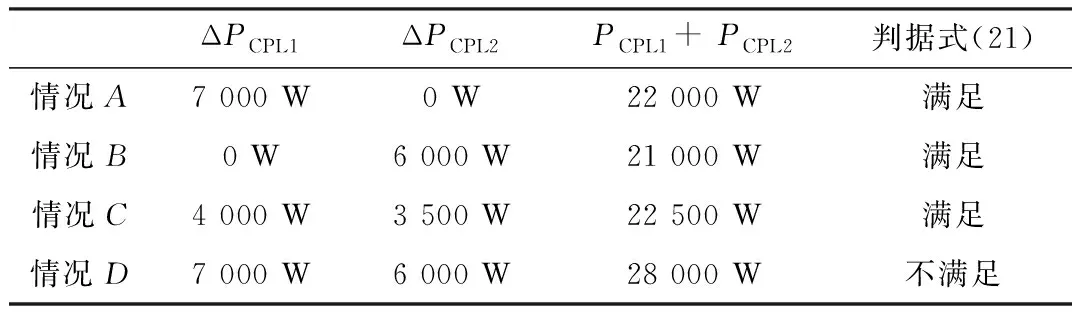
表2 微网群大扰动变化参数

表2中，情况A为子微网1的大容量负载投入；情况B为子微网2的大容量负载投入；情况C为光照降低时，子微网1和子网2的CPL同时跌落；情况D为子微网1和子网2的大容量负载同时投入。

情况A发生，即子微网1大容量负载投入，导致子微网1中CPL阶跃变化，满足稳定性判据式(21)，设置合适的DC-DC变换器传输功率PDC-A可令微网群保持大信号稳定。仿真PDC-A=3 500 W，情况A时的子微网直流母线电压如图6所示。

图6 情况A时子微网直流母线电压Figure 6. Sub-microgrid DC bus voltage in case A

由图6可以看出，在t=1.5 s时，设置合适的DC-DC变换器参考功率，即PDC-A=3 500 W时，电压出现微小波动；在t=2.5 s时，子微电网1中CPL阶跃变化，由于微网群中子微网之间互为储能单元的特性，使子微网1依旧维持稳定运行。子微网2为子微网1输送功率，且子微网2系统仍保持稳定运行。因此，情况A仿真结果符合稳定性分析结果。

同理，情况B和情况C发生时，即子微网2大容量负载投入和光伏骤降，满足稳定性判据式(21)。设置合适的DC-DC变换器传输功率PDC即可令微网群保持大信号稳定。本文设置PDC-B=3 000 W，PDC-C=500 W，则情况B和情况C时子微网直流母线电压如图7和图8所示。

情况D时，子微网1中CPL阶跃变化较大，不满足直流微电网群大信号稳定性判据式(21)，此时没有合适的DC-DC变换器传输功率PDC-C可令微网群保持大信号稳定。仿真通过设置DC-DC变换器传输功率PDC-D，使子微网1达到大信号稳定的临界值，即PDC-D=1 924.64 W，此时子微网直流母线电压如图9所示。

图7 情况B时子微网直流母线电压Figure 7. Sub-microgrid DC bus voltage in case B

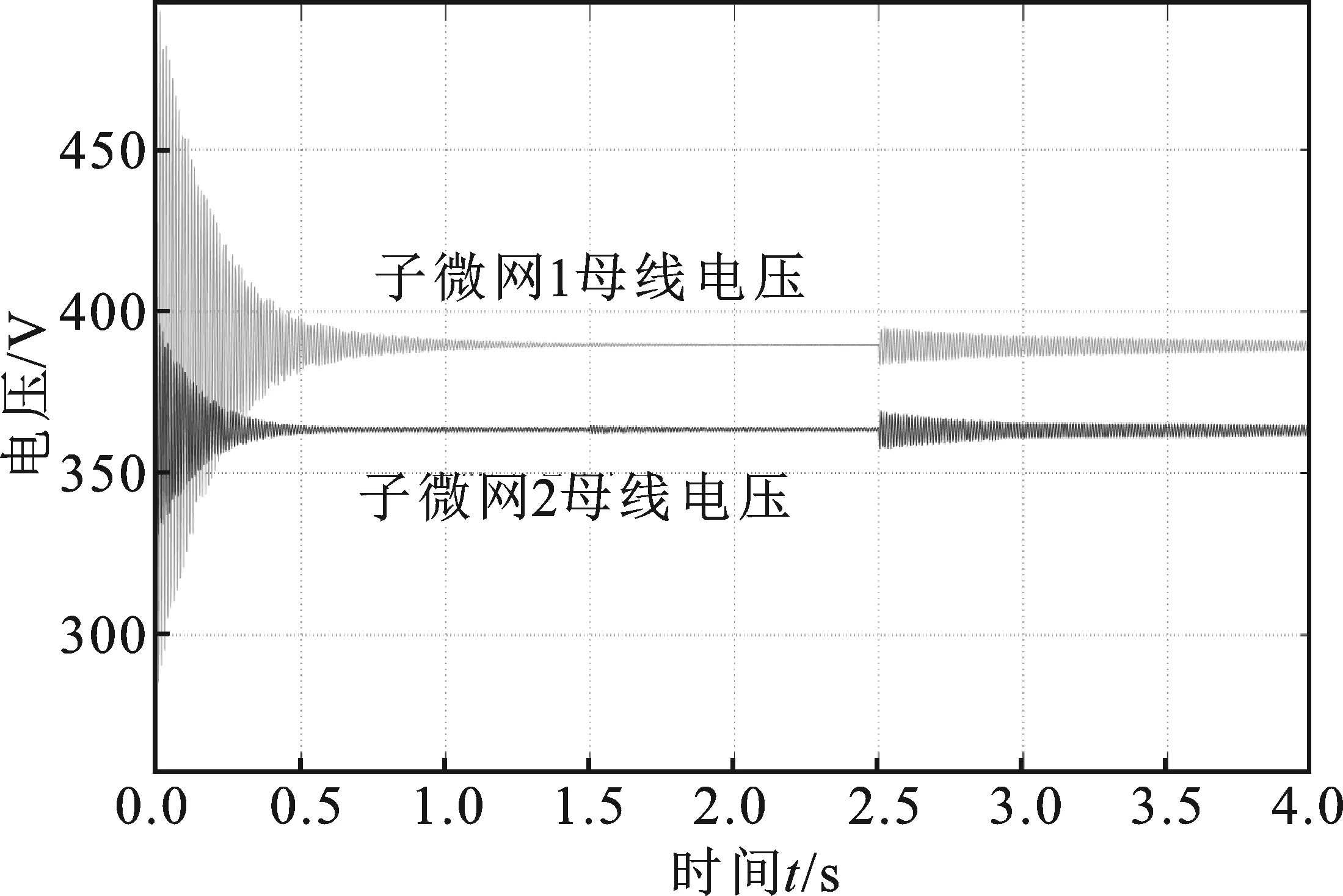
图8 情况C时子微网直流母线电压Figure 8. Sub-microgrid DC bus voltage in case C

图9 情况D时子微网直流母线电压Figure 9. Sub-microgrid DC bus voltage in case D

由图9可以看出，在t=2.5 s发生阶跃变化后，两个系统都逐渐大幅震荡，不能保持稳定运行，即使PDC-D选取临界值，微网群仍不能稳定运行。因此，情况D仿真结果符合稳定性分析结果。

综上所述，直流微电网群的子微网中CPL发生变化，只要变化参数满足直流微电网群大信号稳定性判据式(21)，就能选取到合适的DC-DC变换器传输功率PDC，使直流微电网群保持大信号稳定运行。

5 结束语

传统的混合势函数只能对单个直流电网进行稳定性分析，目前也没有相关研究对直流微电网群进行大信号稳定性分析。本文根据DC-DC变换器等效模型搭建了直流微电网群等效电路图，建立了直流微电网群的混合势函数模型，推导出直流微电网群大信号稳定性判据，并对其进行分析，得出以下结论：当直流微电网群中的CPL阶跃变化，且变化后仍然符合直流微电网群稳定性判据式(21)，则直流微电网群可通过DC-DC变换器设置合适的参考功率PDC，使直流微电网群保持大信号稳定；反之，则直流微电网群不能保持大信号稳定。然而该结论只是通过理论推导和仿真验证所得出的，其在实际应用中的效果还需进一步的验证。