基于深度强化学习算法的财务机器人任务分配的研究

刘 星，张文娟，廖帅元

（1.国网湖南省电力有限公司 信息通信分公司，长沙 410007；2.长沙凯钿软件有限公司，长沙 410000）

0 引言

任务分配的主要研究方法可分为两种：固定分配方法和综合评估方法。固定分配方法：按要求设置好每个任务的执行用户。该方法存在一定缺陷，即不能随着系统和实际任务的变化而灵活设置任务的执行用户。综合评估方法：通过考虑各方面因素，综合评估每个时刻可能发生的不同情况和影响因子（如负载、工作能力水平等），以此进行任务分配。财务机器人采用综合评估的思想，以工作任务进度自动计算规则作为深度策略梯度方法的重要依据，得到最大的总奖赏。

近年来，深度学习、强化学习是机器学习领域的一个研究热点，应用广泛。深度学习侧重对事物的感知，强化学习更侧重解决问题，因此采用深度学习算法以及自定义策略梯度优化任务执行路径，为任务分配提供新的思路，从而找到全局最优解。

1 任务分配数学模型

1.1 问题描述

目前输配电成本监审日常工作仍旧采用人工方式进行工作安排、电话沟通、纸质传递和报送等工作，缺少对整体工作计划的有效管理手段，工作范围上存在遗漏缺少情况，工作进度上无法及时准确地把控和监管，工作过程中信息传递和沟通不畅通，部门工作配合方面步伐不一致，工作的组织和开展零散、效率不高，工作成果的质量低，亟待建设相应的信息化项目来满足实际成本监审和监管的工作需要，做到工作事前有计划、事中有监管（进度和质量）、事后有评价，提升精益管理水平。

在财务机器人工作分配中通常包括人工分配任务以及自动分配任务。在任务分配过程中，由于系统缺少对用户工作经验、用户任务完成度的评估，而引起任务分配不均衡。这种情况通常会降低工作效率。因此任务均衡分配极其重要。

1.2 任务分配的主要因素

在财务机器人中，任务和用户及其任务完成情况是任务分配的核心影响因素。由于每个任务和用户都存在不同的属性值，因此在财务机器人工作任务分配问题中，依据主要的工作任务进度自动计算规则判定该用户是否是最合理的任务执行者。

工作任务进度自动计算规则是由开发者根据以往的工作经验，合理得到的一组判定任务完成进度的算法。进度自动计算结果=A*B*C,其中B 和C 支持自定义。其中A 表示任务提交次数，如表1；B 表示任务收集状态，如表2；C 表示任务审核状态，如表3。

表1 提交次数

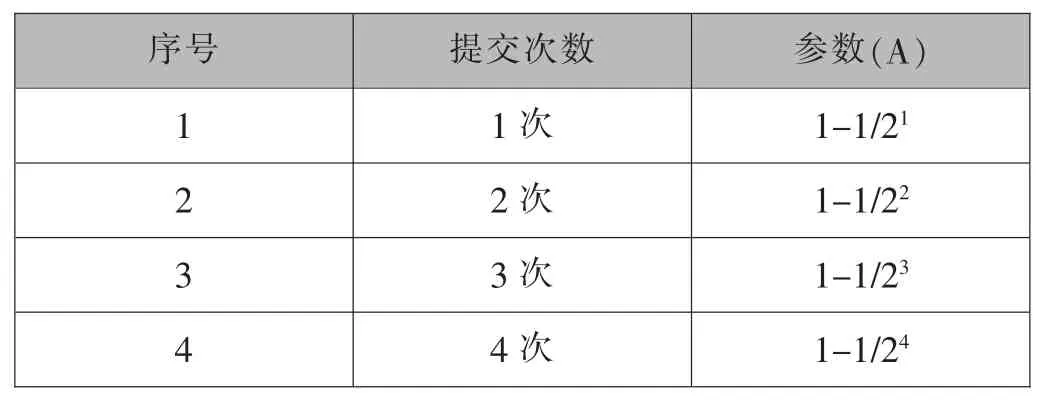
表2 收集状态

表3 审核状态

为了提高财务机器人的工作效率，达到最高点，需构造工作任务进度自动计算规则，让任务分配均衡达到最好，因此构造任务分配总体达到最优目标函数是必要的。

2 算法分析

深度强化学习（Deep Reinforcement Learning，DRL）是人工智能领域新的研究热点，DRL 是由具有感知能力的深度学习（Deep Learning，DL）和具有决策能力的强化学习（Reinforcement Learning，RL）相结合产生的。DL 的基本思想是通过多层的网络结构和非线性变换，组合底层特征，形成抽象的、易于区分的高层表示，已发现数据的分布式特征表示。RL 的基本思想是通过最大化智能体（Agent）从环境中获得的累计奖赏值，以学习到完成目标的最优策略。其中DQN 作为经典算法之一，它用一个深度网络代表价值函数，依据强化学习中的Q－Learning，为深度网络提供目标值，对网络不断更新直至收敛。由于DQN 是基于Q－Learning，如果输出DQN 的Q 值，可能会发现，Q 值非常大，这时QLearning 预测目标值的时候可能出现overestimate，对于这一类问题，我们可采用DDQN 解决。

本文采用DQN 算法、DDQN 和轮询调度三种算法，其中DQN 和DDQN 融合了强化学习的Q－Learning和深度神经网络，本文将探索哪一种算法能更快地求取合理的任务分配。

2.1 DQN 算法

DQN 包含状态（state）、行动（action）和奖励（reward）三个要素。reward 值静态描述了各个状态之间转移的立即奖励值，行动则决定状态之间的转移规则。QLearning 迭代时采用立即奖励值、Q 值函数和折扣率共同组成评价函数，Q 值表中保存各状态行动对（s，a）的估计值。Q－Learning 算法在给定策略h（x）下，在状态S采取行动A的评价函数为：

式中：α∈（0，1）为学习步长；γ∈（0，1］为折扣率，决定agent 以多大权重考虑未来奖励；t 为时间步；R为在采取当前（S，A）的立即奖励；max 函数表示算法会根据下一个（S，A）中预测值的最大值来评价（S，A）；式中R＋γ max Q（S，a）－Q（S，A）定义为时间差分误差（TD error），算法通过TD error 对估计值递增更新直到收敛，行动选择常采用ε－greedy 策略。将agent从开始状态转移到目标状态整个过程称为一次情景（epsiode），在episode 中每次状态转移的时刻称为一个时间步（time step）。

Deep Q－Learning 算法流程如下：

（1）首先初始化“样本集”（Memory D），简称D，它的容量为N，初始化Q 网络，随机生成权重ω，初始化target Q 网络，权重为ω-=ω，循环遍历episode=1，2，…，M：初始化initial state S1；

（2）循环遍历step=1，2，…，T：用∈-greedy 策略生成action at（以∈概率选择一个随机的action，或选择at=maxaQ（S，a；ω））；

（3）执行action at，接收reward rt 及新的state S＋1；

（4）将transition 样本（S，a，r，S）存入D 中；

（5）从D 中随机抽取一个minibatch 的transitions（S，a，r，S）；

（6）如果j＋1 步是terminal 的话，令y=r；否则，令y=r＋γ maxa′Q（S，a′；ω-）；

（7）对（y-Q（S，a；ω））2 关于ω 使用梯度下降法进行更新；

（8）每隔C steps 更新target Q 网络，ω-=ω。

（9）输出原始问题的最优策略h*（x）为在各状态下贪婪地选择Q 值最大的行动。

2.2 DDQN 算法

DDQN 网络结构和DQN 一样，也有一样的两个Q网络结构。在DQN 的基础上，通过解耦目标Q 值动作的选择和目标Q 值的计算这两步，来消除过度估计的问题。在DDQN 这里，不是直接在目标Q 网络里面找各个动作中最大Q 值，而是先在当前Q 网络中先找出最大Q 值对应的动作，即

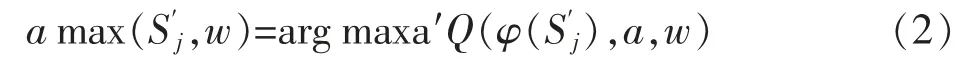
然后利用这个选择出来的动作amax（S，w）在目标网络里面去计算目标Q 值。即：

综合起来写就是：

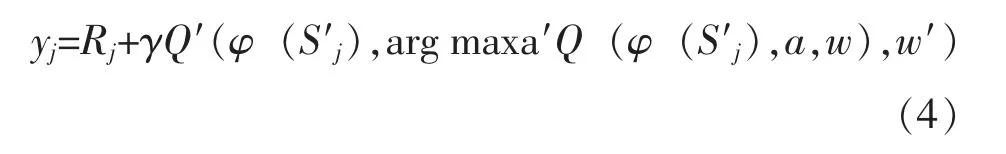
DDQN 算法流程如下：

（1）随机初始化所有的状态和动作对应的价值Q，且随机初始化当前Q 网络的所有参数w，初始化目标Q 网络Q′的参数w′=w。清空经验回放集合D。

（2）进行迭代。

1）初始化S 为当前状态序列的第一个状态，拿到其特征向量φ（S）；

2）在Q 网络中使用φ（S）作为输入，得到Q 网络的所有动作对应的Q 值输出。用∈-贪婪法在当前Q 值输出中选择对应的动作A；

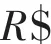
4）将｛φ（S），A，R，φ（S′），is_end｝这个五元组存入经验回放集合D；

5）S=S′；

6）从经验回放集合D 中采样m 个样本｛？（S），A，R，φ（S′），is_endj｝，j=1，2，…，m，计算当前目标Q 值y：

7）使用均方差损失函数1／m∑j=1／m（y-Q（φ（S），A，w））2，通过神经网络的梯度反向传播来更新Q 网络的所有参数w；

8）如果T%C=1，则更新目标Q 网络参数w′=w；

9）如果S′是终止状态，当前轮迭代完毕，否则转到步骤2）。

2.3 轮询调度算法

轮询调度算法是简洁的，无须记录所有用户任务分配情况，只需要把任务依次按顺序轮流分配给用户，当用户都分配了任务后，还需要继续分配，则重新开始循环。

3 任务分配流程

（1）学习环境设计：通过和环境进行交互，利用不确定的环境奖赏来发现最优行为序列。本文提出的学习环境主要根据调度方案包含工作任务进度完成度建模，获取当前调度方案下完成任务所需的时间，从而对当前调度方案针对调度目标的优劣进行评估。

（2）动作集：动作集是为Q 学习算法的可以选择执行动作的集合。本文通过工作任务自动计算规则，充当Q 学习算法的动作集合。

（3）状态变量确定和状态空间划分：该因素是Q 学习算法合理选择动作的基础，为了使得算法更好地选择工作任务自动计算规则，实现优化调度目标，必须完成算法状态空间的离散化和定量化。

（4）惩罚函数：惩罚函数的设计目的在于对算法每次动作执行后的优化效果进行奖惩。对于优化的动作，进行奖励，使得该动作具有较大的选取概率；对于不优的动作，进行惩罚，减小该动作的选取概率。

（5）算法流程：根据上述Q 学习算法相关定义，最后确定算法的流程。

算法实现步骤如图1 所示。

图1 优化算法实现步骤

4 仿真校验

为了验证上述方法的均衡性以及工作效率，选择本文提出的DQN 算法、DDQN 算法和轮询调度方法进行实验对比分析。

4.1 用户所获得各类任务比例

三种方法的用户所获得的类别任务比例分别如图2、图3、图4 所示。从图2 可以看出，对于不同的任务，4个实验用户分配到的任务数量基本一致，并没有按照用户完成任务的效率合理分配任务；从图3 可以看出，根据不同的任务类型，4 个实验用户分配到的任务数量完全不一样，可以推断出DQN 算法可以给用户合理地分配任务；从图4 可以看出，DDQN 与DQN 任务分配占比相似，可推断DDQN 算法可用于任务分配问题。用户对于该任务完成度越高，被分配的任务量也就越多，并且随着其他一些任务或用户属性的影响，任务量与工作进度之间的关系还可以产生动态变化，说明深度强化学习算法可以有效的按照工作进度合理分配任务。

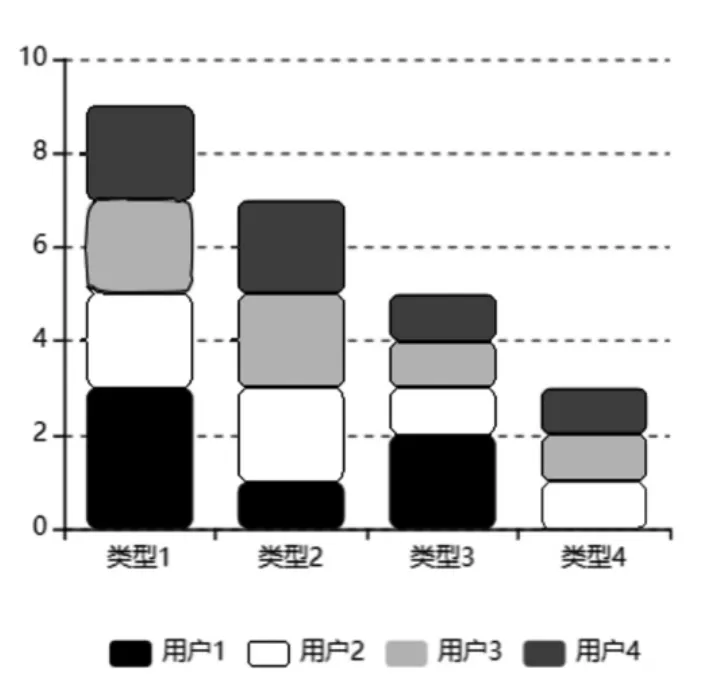
图2 轮询调度法

图3 DQN 算法

图4 DDQN 算法

4.2 深度强化学习训练结果分析

因为DQN 和DDQN 算法区别在于Q－target 的计算，所以两者神经网络结构一样，结构图如图5 所示。其中target_net 与eval_net 采用相同的网络架构和不同的参数。

图5 神经网络结构图

采用DQN 算法得到的损失结果展示如图6 所示。采用DDQN 算法得到的损失结果展示如图7 所示。由图可知随着训练步长的增加，损失值在不断减小，表明该函数更加趋近于最优解。

图6 DQN 函数损失图

图7 DDQN 函数损失图

5 结论

本文通过系统地分析任务分配问题的特点，提出了财务机器人任务分配问题的数学描述，采用深度强化学习算法（DQN、DDQN）解决任务均衡分配问题。这两种方法收敛速度快，可以有效地处理连续动作集的问题，弥补了后者初期解决速度慢的缺点。实验结果表明，该方法适用于财务机器人，在性能上优于传统的任务分配方法（轮询调度法）。