反拱形爆破片翻转行为数值模拟研究
钱志强,章碧成,施 威,郭月龙
(中国工程物理研究院 机械制造工艺研究所,四川绵阳 621900)
0 引言
反拱形爆破片的爆破过程中涉及“失稳翻转”和“破裂”两个阶段[1]。大量的试验与研究表明反拱形爆破片翻转时间极短,一旦发生失稳即爆破,因此可以将爆破片的翻转压力作为爆破压力进行研究[2-4]。由于反拱形爆破片翻转压力的影响因素众多,通过试错法进行摸索耗时耗力耗财且未必能得到理想的结果。近十几年来,随着计算机的普及与算力的提高,越来越多的学者采用有限元计算的方法对反拱形爆破片的失稳载荷进行计算,然后通过试验验证与仿真结果进行对比迭代的方法加速设计,并越来越得到广泛的认可[5-6]。
罗代明等[7-8]利用Ansys软件,简化了夹持力、装配状态等因素,直接对反拱形爆破片进行建模,采用弧长法进行非线性屈曲分析,最终模拟翻转压力与实际值误差在10%以内。汤来鑫[9]利用Abaqus软件综合考虑了夹持力,装配关系等因素,采用弧长法进行非线性屈曲分析,模拟结果显示失稳载荷受夹持力、装夹状态、摩擦系数等因素影响。目前对反拱形爆破片的数值模拟方法多采用非线性屈曲分析,通过逐步增加载荷水平来寻找结构变得不稳定时的临界载荷[10]。该方法综合考虑了结构的稳定性与强度问题,与特征值分析相比通常比较准确,可用于实际结构的设计或评估[11-13]。但在实际使用过程中,该方法往往会因为载荷-位移曲线存在阶跃或回跃响应的问题,对结构的精确屈曲载荷与后屈曲问题(失稳后的变形,即翻转行为)难以收敛。
本文研究的反拱形爆破片同时涉及夹紧力、装配关系、翻转后冲击锥尖破裂等强非线性问题,且加载形式为慢速加载,在时间历程上包含大时间步的稳态加载与极小时间步的瞬间屈曲失稳。采用隐式算法难以收敛,采用显式算法无法体现稳态加载过程导致结果误差大。针对上述问题,采用LS-DYNA隐-显自适应切换技术,综合了隐式算法大时间步下高计算精度与显式算法强非线性的优点,有效地模拟了反拱形爆破片稳态加载与瞬间失稳翻转的非线性屈曲过程,并揭示了其翻转机理。
1 材料与方法
反拱形爆破片爆破试验在某单位爆破试验装置上进行,爆破试验工装如图1~3所示。试验用反拱形爆破片材料为316L平箔片,通过气压成形的方式冲压成形,冲压模具的形状根据反拱形爆破片的几何尺寸进行设计。反拱形爆破片的实物与结构如图1、图2所示。助爆锥的结构如图3所示,该助爆锥结构为在圆环端面上预制环形凹槽,控制靠近内孔处保留约0.02 mm的刃口宽度。该助爆锥结构相比于传统结构弱化了锥尖的“刺破”作用,采用反拱形爆破片翻转时的“高速冲击”作用致破,完成快速泄压。爆破过程采用慢速加载的方式,采用气压传感器实时监测进气端的气压变化,采用小流量阀门调节的方式控制气压上升速率不大于0.1 MPa/s。

图1 爆破试验工装

图2 爆破片模型

图3 助爆锥模型
2 有限元模型构建
2.1 FEM模型的设置
以表1列出的几何参数为例,建立了反拱形爆破片的有限元模型,如图4所示。

表1 爆破片、助爆锥及铜垫几何尺寸
由于仅在爆破片翻转过程采用显式动力学计算,时间极短,整个仿真过程以隐式为主,爆破片采取等厚度建模,采用-16号壳单元[14],对助爆锥与上方施加预紧力的铜垫采用2号实体单元,助爆锥底面约束X,Y,Z方向的平动自由度,对铜垫和助爆锥侧壁约束X,Y方向的平动自由度。对反拱爆破片施加大小为12 MPa的压力载荷,作用时长120 s,载荷加载形式为斜坡加载。对铜垫施加15 000 N的预紧力来模拟实际装夹情况。隐式求解采用瞬态动力方法求解,随时间施加的载荷曲线如图5所示。
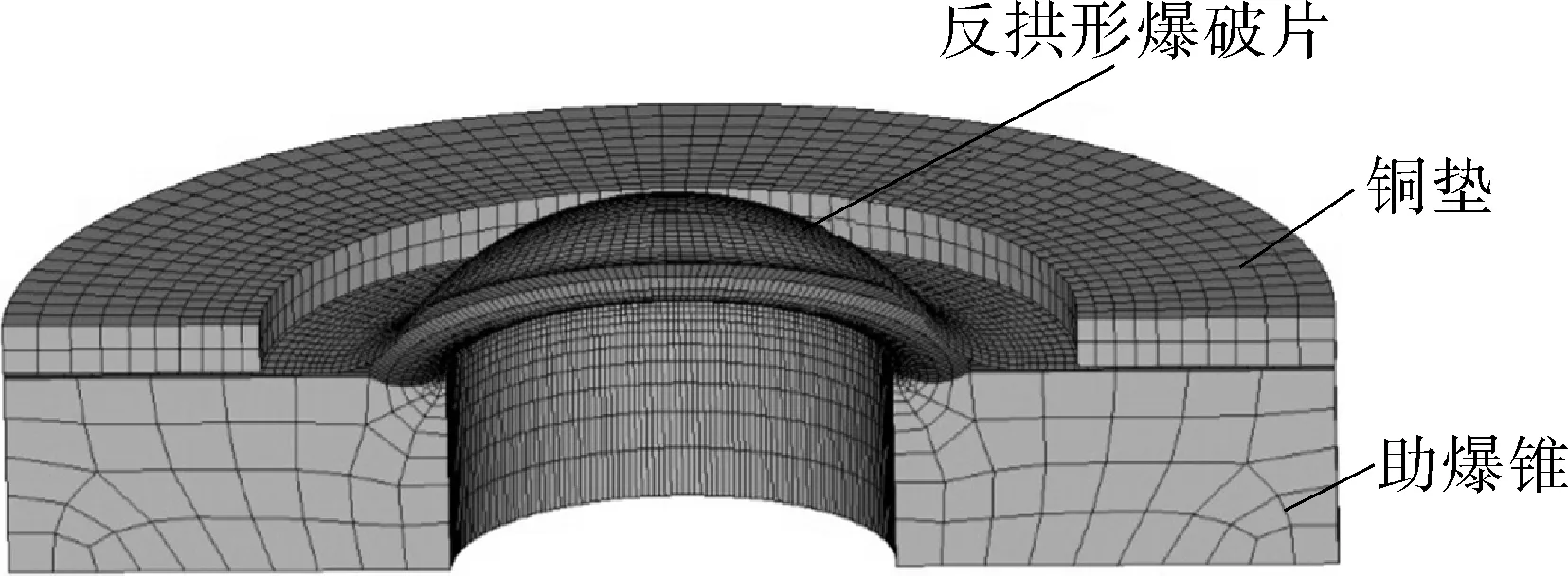
图4 反拱形结构FEM模型
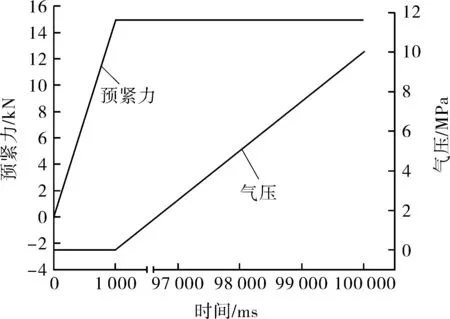
图5 预紧力与气压随时间加载的曲线
2.2 材料定义与本构
爆破片与调整垫材料均为316L不锈钢,铜垫为H62。其中爆破片为316L箔材,通过单向拉伸试验获得其名义应力-应变曲线,而后转换为真实应力-应变曲线用于仿真计算,如图6所示,弹性模量取193 GPa,泊松比取0.25。
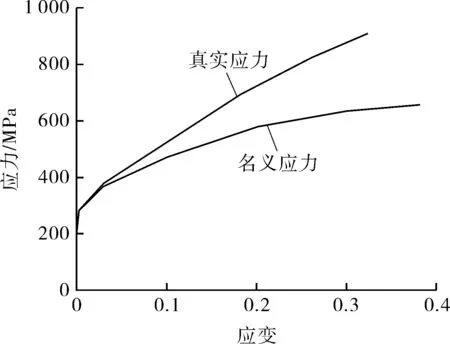
图6 316L箔材的应力-应变曲线
采用分段线性塑性材料本构模型,采用Cowper-Symbols模型考虑应变率的影响,它与屈服应力的关系为:
(1)

2.3 隐-显自适应求解设置
爆破片慢速爆破试验的实际加载时间大于10 min,爆破片结构随着载荷的缓慢加载首先发生细微变形,当达到临界载荷后迅速翻转完成爆破。本文采用的隐式-显式自适应切换方法综合了隐式求解与显示求解两种方法的优点,计算时首先采用隐式计算方法,设置一个较小的最小时间步(大小取决于显示求解时长,即翻转过程时长),采用完全牛顿-拉普森方法进行自动时步控制,通过隐式求解方法不断迭代逼近精确临界载荷,当达到临界载荷后,隐式求解失败,显示求解程序启动,在设定的极短时间内进行求解,求解结束后切换回隐式求解程序,若是此时还未完成翻转,则隐式求解程序依然不收敛,继续切换为显式求解程序,直至完成爆破片翻转过程的计算,而后切换回隐式求解程序,完成计算。计算流程示意如图7所示。采用此方法可以避免反复的人工调试,全程由计算机自动执行便可以计算出精确的屈曲载荷与翻转过程。

图7 计算流程示意
3 反拱爆破片翻转行为计算结果与验证
3.1 计算结果
首先针对简化后的助爆锥结构进行模拟计算与验证。试验结构如图8所示,保持反拱形爆破片几何尺寸同表1,助爆锥内直径分别取5.8 mm和4.0 mm,设置助爆锥为刚体,计算结果如图9所示。

图8 简化的反拱爆破片试验结构
图9为试样1的模拟计算结果。施加完预紧力后爆破片的等效应力分布云图如图9(a)所示,可以看到预紧力对冲击片的拱面应力状态无任何影响;随着气压的缓慢加载,冲击片的根部首先发生塌陷,随后在气压的作用下被“贴平”在助爆锥上,此过程随着气压的加载而不断重复,直至气压达到2.3 MPa时冲击片“贴合”至助爆锥边缘,如图9(b)所示;由于缺少助爆锥的支撑作用,爆破片从根部发生屈曲失稳(见图9(c)(d)),此时对应的气压为2.8 MPa,随后爆破片迅速发生翻转(见图9(e)),最终爆破片翻转完成(见图9(f)),整个翻转过程在0.1 ms以内完成。

图9 调整垫内直径5.8 mm下的爆破过程计算结果
减小助爆锥内直径为4 mm,保持其余设置不变,试样2的模拟计算结果如图10所示。可以看到,随着气压的加载,爆破片根部区域的斜率也在逐渐增大,对应的气压不断升高,如图10(b)(c)所示。当气压达到7.3 MPa时爆破片根部达到稳定状态不再变化,对应的根部直径为5.3 mm,如图10(c) 所示。在该状态下,爆破片整体结构的相对“薄弱点”转移至顶部,随着气压的进一步加载,爆破片从顶部区域开始屈曲失稳,如图10(d) 所示,随后迅速完成翻转,并在翻转过程中高速冲击助爆锥完成爆破。

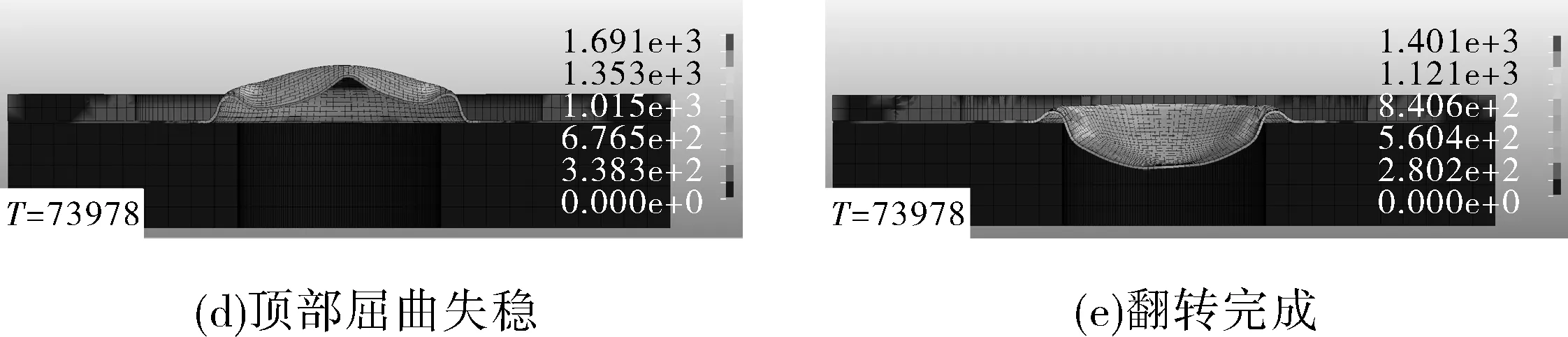
图10 调整垫内直径4 mm下的爆破过程计算结果
对比试样1与试样2的计算结果,可以发现反拱形爆破片在承载过程中存在“根部自稳定”现象,其根部区域的承载能力会随着载荷的增加而自发地增强。对于某一几何尺寸固定的反拱形爆破片,助爆锥内直径存在一临界点,对于本节中的反拱形爆破片对应的助爆锥内直径临界点为5.3 mm,当助爆锥内直径大于5.3 mm时将导致爆破片因缺少助爆锥的支撑作用而无法达到根部稳定状态,引发根部塌陷的翻转模式,此种情况下翻转压力随助爆锥内直径的增大而减小;而当助爆锥内直径小于5.3 mm时,由于根部稳定状态的存在引发顶部塌陷的翻转模式,此种模式下翻转压力与助爆锥内直径无关,仅与爆破片几何尺寸有关。
3.2 模拟结果验证
为了验证仿真计算结果的准确性,制造加工了内直径分别为5.8 mm与4 mm的助爆锥,模拟与试验结果如表2所示。可以看出,当调整垫内直径为5.8 mm时,试验过程观察到冲击片在2.13 MPa左右完成翻转,可听到轻微的翻转声,但未发生爆破;当调整垫内直径减小为4 mm时,在6.84 MPa气压下发生爆破。两种不同尺寸助爆锥下的试验结果与仿真结果的误差保持在0.6 MPa 以内。考虑到实际爆破片成形后拱面发生一定程度的减薄、根部区域存在残余应力,在未考虑上述因素的情况下,模拟计算取得了相当高的精度。

表2 试验翻转压力结果
4 带槽形助爆锥对反拱形爆破片爆破压力的影响
根据前文研究结果,反拱形爆破片在助爆锥支撑足够的情况下将逐渐达到“根部稳定”状态,对应其承载能力不断提高,最终达到结构屈曲载荷。屈曲载荷数值的大小与反拱形爆破片屈曲前的形状直接相关。带槽形助爆锥通过在圆环面上加工出一定形状的环形凹槽从而实现对反拱形爆破片屈曲前形状的改变,进而改变爆破片的屈曲载荷。
本节针对表1所示几何参数,图11所示反拱形结构开展数值模拟计算与试验验证,研究助爆锥凹槽对反拱形爆破片爆破压力的影响。

图11 带槽形助爆锥的反拱爆破片结构
计算结果如图12所示。受环形凹槽影响,反拱形爆破片在加载过程中存在2次“屈曲失稳”阶段。施加载荷后,反拱形爆破片的根部区域首先发生塌陷,与凹槽的锥尖发生接触,如图12(a)所示,此为第一次屈曲,并以锥尖为支点形成稳定结构。

(a)爆破片与锥尖发生接触(一次屈曲)
由于根部区域并未自发形成根部稳定状态,此时爆破片的根部区域仍然为整体结构的薄弱点,当气压为4.2 MPa时,爆破片在锥尖处发生二次屈曲失稳,如图12(b)所示,随后爆破片以根部塌陷模式进行翻转,如图12(c)(d)所示。根据图12所示的计算结果可以发现,由于助爆锥凹槽尺寸与爆破片尺寸并未形成良好匹配,导致爆破片在一次屈曲时提前与锥尖发生接触,破坏了“根部自稳定”现象的发生,最终导致爆破片以较低的压力进行翻转。
依次减小助爆锥凹槽中心直径进行模拟计算,计算结果如表3所示,试验结果如表4和图13 所示。

表3 不同凹槽中心直径下的爆破片一次屈曲与翻转压力模拟结果

表4 不同助爆锥凹槽中心直径下的爆破片爆破压力试验结果

图13 不同凹槽中心直径下爆破压力的模拟值与实际值
可以看出,受实际材料参数、加工精度等因素影响,模拟结果与实际结果有小于1 MPa的误差,但是仿真结果与试验结果的趋势保持一致。如图14所示仿真结果,当凹槽中心直径从6.8 mm减小到6.0 mm,爆破片一次屈曲后不再与锥尖发生接触,在“根部自稳定”现象的作用下爆破片的翻转压力从3.4 MPa提高至8.8 MPa,对应其塌陷模式由根部塌陷向顶部塌陷转变(见图15);此外,随着翻转压力的升高,致破性能由翻转未爆破向翻转即爆破转变,如图16所示。

图14 不同凹槽中心直径下爆破压力的模拟结果
随着凹槽中心直径进一步减小,反拱形爆破片的塌陷模式仍然为顶部塌陷,但其翻转压力由8.84 MPa下降至7.35 MPa,爆破性能由翻转即爆破向翻转后点漏转变。提取不同凹槽中心直径下的反拱形爆破片二次屈曲前截面形状,如图17所示。可以看出,随着凹槽中心直径的下降,爆破片二次屈曲前的拱高逐渐下降,导致整体形状的“陡峭”程度下降,使得结构承载能力下降,最终反映为爆破片的翻转压力与致破性能的下降。

(a)中心直径6.8 mm

图16 凹槽中心直径对致破能力的影响
综上所述,针对几何尺寸固定的反拱形爆破片,带槽形助爆锥一方面通过改变爆破片的翻转模式进而影响其翻转压力与致破性能;另一方面在顶部塌陷翻转模式下通过改变爆破片二次屈曲前的形状来影响爆破片的翻转压力与致破性能。带槽形助爆锥几何尺寸需与爆破片尺寸形成良好的匹配才能实现翻转压力与致破性能的较优组合。
5 结论
(1)基于LS-DYNA的隐-显自适应切换方法能有效地模拟反拱形爆破片的爆破压力与翻转行为。
(2)反拱形爆破片在承载过程中存在“根部自稳定”现象,其翻转行为根据助爆锥与爆破片尺寸匹配程度的不同表现为顶部塌陷的高压力翻转与根部塌陷的低压力翻转。顶部塌陷模式相比于根部塌陷模式具备更优异的致破性能。
(3)针对文中的反拱带锥形爆破片,随着助爆锥凹槽中心直径的减小,爆破片的爆破压力先迅速增大后缓慢减小。选择偏小的助爆锥凹槽中心直径可获得较高的爆破压力并提升爆破压力对助爆锥尺寸的不敏感性。

