日本初中教科书尺规作图编排及启示
何煜晶 周 超 (苏州大学数学科学学院 215006)
1 前言
尺规作图,即有限次使用直尺和圆规,解决平面几何的作图问题[1].它是将想象中的几何概念变成看得见的几何的重要手段,帮助学生直观理解几何概念及其关系,形成初步的几何直觉.《义务教育数学课程标准(2011年版)》(下文简称《课标》)将尺规作图置于基本几何概念(点线面角、相交线平行线、垂线、三角形、四边形、圆等)之后[2].尽管《课标》并未规定教科书中知识内容的呈现顺序,但实际的教科书编写还是受到《课标》中尺规作图后置的影响,初中数学教科书中有关尺规作图的内容也出现较晚.因此,尺规作图成为了一种学习任务,其在帮助学生理解几何概念与实际操作等方面的功能被大大削弱,影响了早期的直观运用.
2017年,日本开始了最新一轮的数学教育课程改革.2017年3月,日本文部科学省颁布了《初中学习指导要领》(相当于我国的《课标》,下文简称《要领》),并于2021年4月1日开始施行.在初中《要领》的指导下,日本编写了新版本的初中数学教科书. 本文主要探讨日本最新初中《要领》及教科书对尺规作图内容的处理与编排,以期对我国《课标》与教科书的编写带来启示.
2 日本初中《要领》中尺规作图的内容与要求
日本初中《要领》将初中数学知识分为数与式、图形、函数、数据的活用(即统计与概率)四个领域,其中每个领域都融入了数学的活动[3],如图1所示.《要领》对每个年级的学习内容进行了说明,与我国《课标》相比,日本《要领》对知识内容的划分更为固定明确.
图1 日本2017年初中 《要领》中数学知识内容
尺规作图属于“图形”领域,日本初中各年级“图形”领域知识内容如表1所示.在七年级平面图形学习之初就有了尺规作图的内容要求.与我国相比,日本《要领》中尺规作图的位置顺序明显靠前.尺规作图对于培养初中生图形领域的资质与能力方面,具有引起学生对图形的兴趣和关心、直观地捕捉图形的性质和关系、促进逻辑思考的意义.
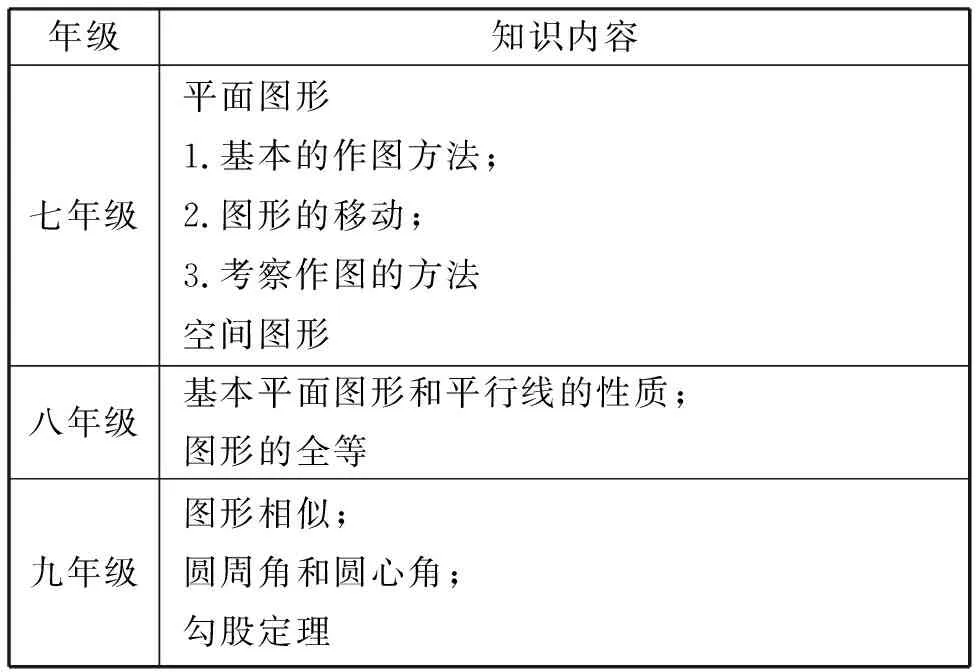
表1 “图形”领域知识内容
《要领》解说还对七年级尺规作图的内容处理提出了建议,强调不要单方面地给出作图的方法,而是着眼于图形的对称性和决定图形的要素,找到作图的方法,并根据图形的性质和关系有条理地对方法进行说明.
3 日本初中教科书尺规作图编排特点
《中学校数学1》由日本学校图书株式会社出版,该出版社成立于1948年,以研究、编写、出版与发行基础教育教科书与教育图书为主要任务,在中小学数学教科书的编写方面发展成熟.2020年9月出版的《中学校数学1》以2017年《要领》为指导,能够充分反映最新《要领》的理念与要求.因此我们以该版本的教科书为例,研究尺规作图的编排特点.
3.1 注重小学与初中的衔接,唤醒学生已有的直观经验
图2是该教科书七年级“图形”领域的章节目录.平面图形章节分为两部分:一是各种角作图,二是图形的移动.第一节“各种角作图”即为尺规作图的内容,内容集中,约占平面图形章节内容的60%.章节目录左侧列出了所需的预备知识.有关尺规作图的学习准备主要是小学阶段学习的垂直与平行、三角形、平行四边形、菱形与圆的相关知识.

图2 日本七年级“图形”领域章节目录
在章节目录旁设置“小学学习准备”栏目,一方面提醒学生“回头看”,回顾已有知识,做好新知识的学习准备,加强小学与初中几何知识之间的联系.另一方面,教师能够据此了解学生的知识基础,方便其备课.
3.2 增加尺规作图的情境性与趣味性
用“宝藏藏在哪里”的情境引入尺规作图的内容.图3为宝藏的线索文件,图4为地图.在线索文件中,宝藏在直线①②③相交而成的三个点所在圆的圆心上.直线①经过地图中路 ○ア的中点,且与路 ○ア夹角为90°;直线②经过点A,且与路 ○イ夹角为30°;直线③经过点B,且与路 ○イ夹角为60°.因此为了找到宝藏,首先需要作出直线①②③.
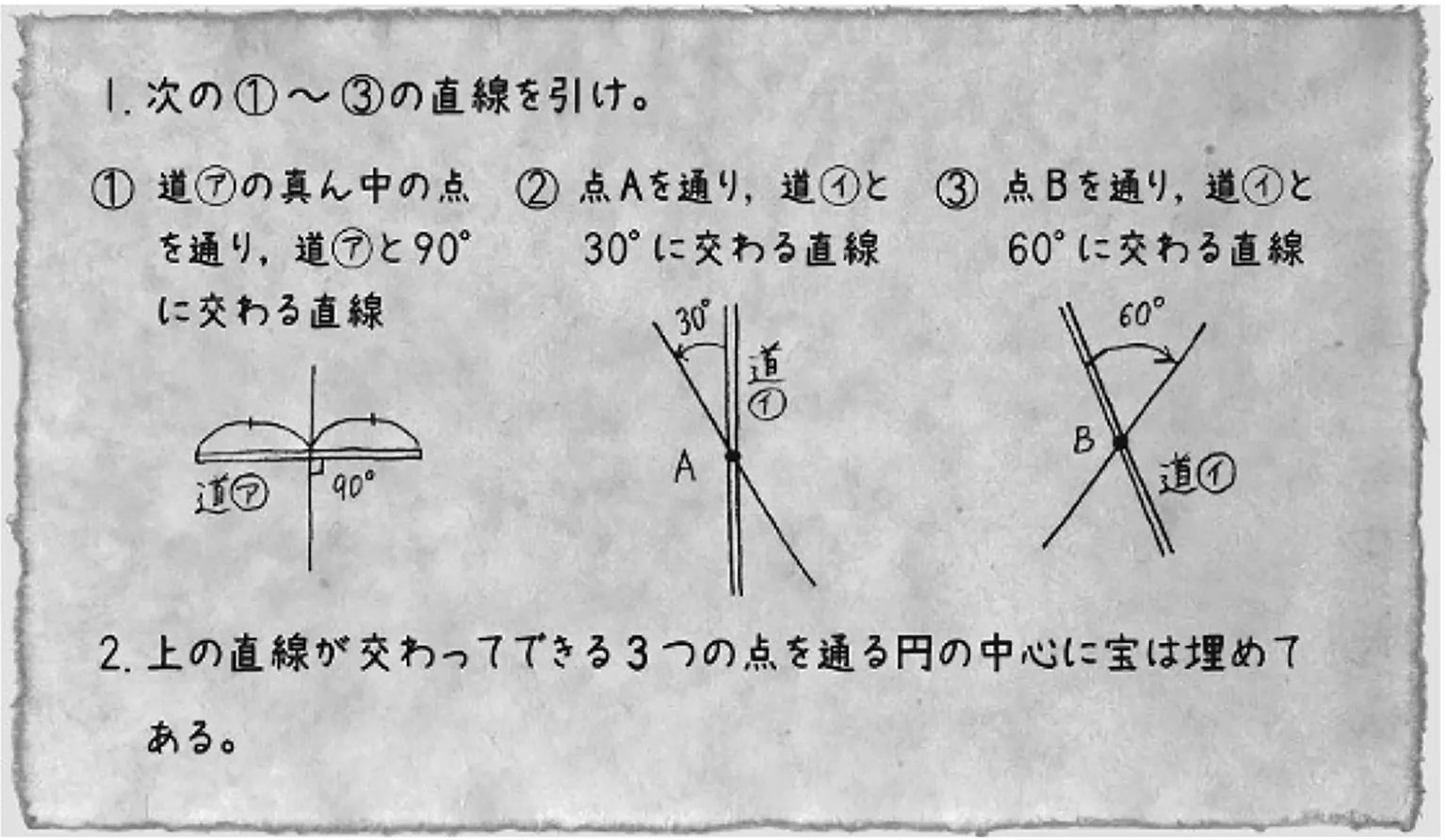
图3 宝藏线索文件
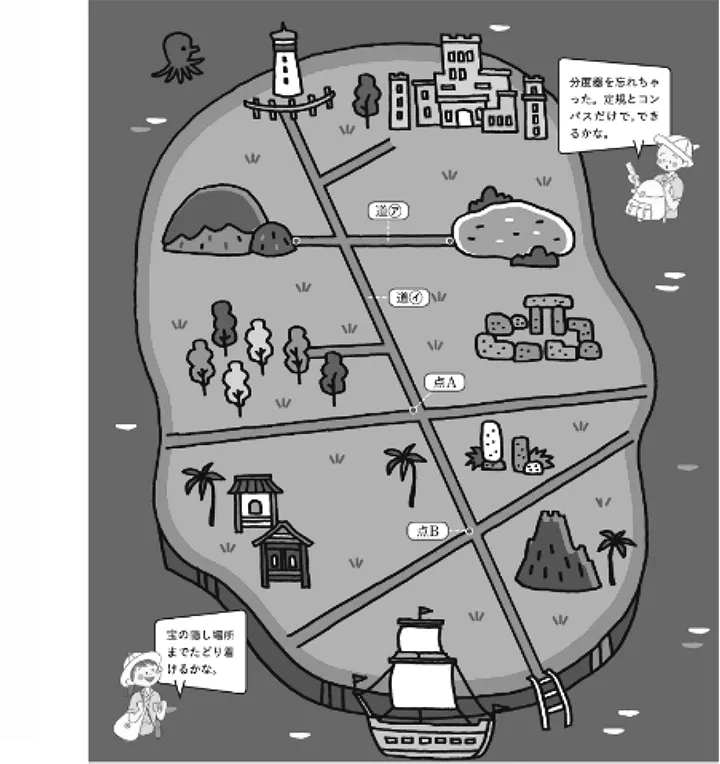
图4 宝藏地图
为了作夹角为90°,30°和60°的直线,最简单的方法是使用量角器.然而在寻宝过程中,发现忘记带量角器了,只带了直尺与圆规.由此引入课题:不使用量角器,如何作出90°,30°和60°角呢?
在该情境下,“各种角作图”内容分为三部分:90°角作图;60°和30°角作图;作图的利用.各部分课时、学习内容及术语符号见表2.

表2 “各种角作图”课时与结构
结合对情境与章节内容结构的分析,该问题情境一方面用寻找宝藏这种带有神秘色彩的活动吸引学生的兴趣,激发学生思考;另一方面,在进行尺规作图的过程中将平面图形的基础知识如垂线、角、平行线、圆等串联起来,使得各知识点的出现顺序较为自然.
3.3 将尺规作图嵌入几何活动中,培养一般化的几何思考方式
日本教科书中垂直平分线、角平分线等内容的作图步骤与我国教科书基本一致,但在内容处理上存在明显差异.我国教科书对于作图的内容处理相当直接,通常给出作法就结束,至于作法从何而来,如何进行思考并未加以说明.日本教科书在尺规作图内容上增加了思考方式,目的是让学生思考作图的角度.此外还设计了尺规作图的数学活动,帮助学生应用尺规作图解决实际问题.
(1)尺规作图的思考方式
以90°角作图为例,日本教科书在作图之前引导学生思考夹角为90°的两条直线所在的图形.日本学生在小学阶段已经学习了菱形的相关知识:菱形是以两条对角线为对称轴的轴对称图形,四条边长度相等,因此菱形的两条对角线互相垂直平分.于是利用菱形对角线的性质,通过作菱形的方式作垂直平分线.
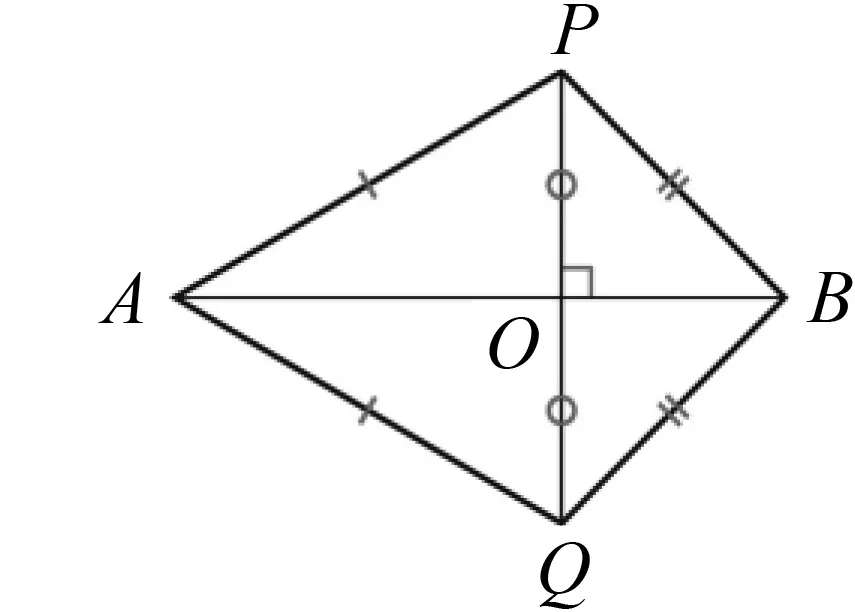
图5 风筝形
在垂直平分线作图的基础上,过直线外一点作已知直线的垂线.教科书同时还给出了另一种作法:利用风筝形进行作图.风筝形是以一条对角线为对称轴的图形.图5即为一个风筝形,对角线AB为对称轴,因此有AB⊥PQ,PO=QO.
利用风筝形的性质,过直线外一点作已知直线的垂线的作图顺序如图6所示.
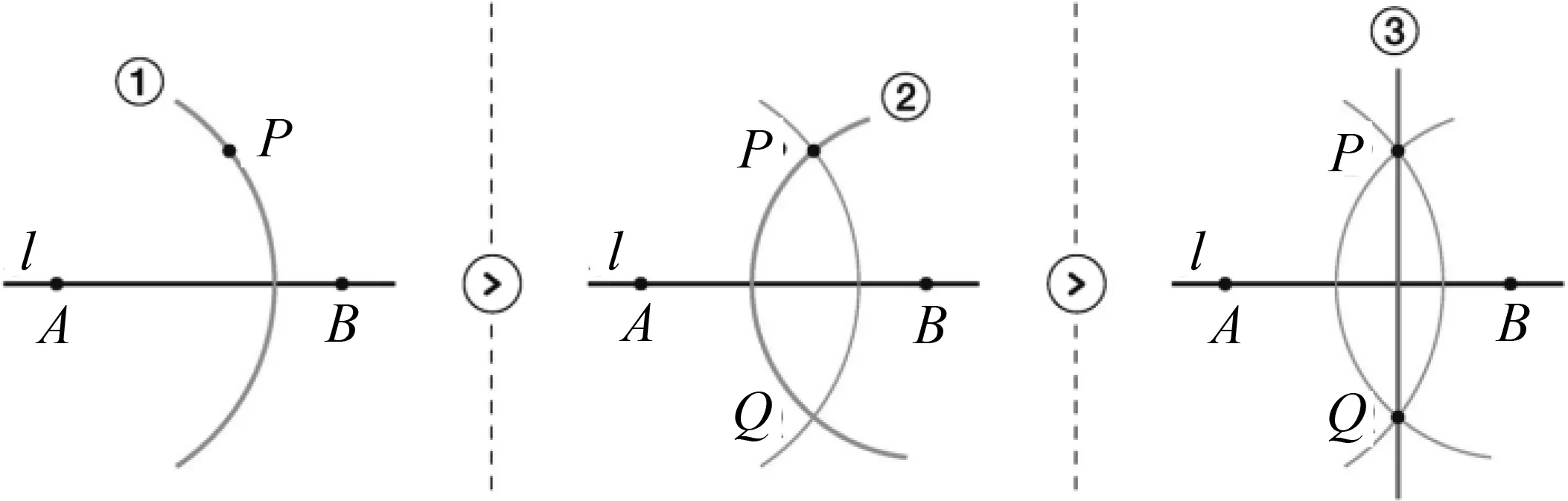
图6 利用风筝形作垂线
将教科书中各种作图的思考方式进行总结(见表3),可以发现,教科书以垂线、垂直平分线与角平分线作图为核心.在思考方式上,都是考虑已学的对称图形,以菱形为主.由于菱形具有对角线互相垂直平分、对角线平分顶角、对边平行等性质,因此在尺规作图学习之初,从菱形性质进行思考是一种不错的选择.

表3 尺规作图的思考方式
(2)尺规作图的数学活动
对于“已知圆上三点找圆心”的内容处理,教科书设计了一个数学活动:将破碎的圆形铜镜碎片进行复原.
该部分内容处于尺规作图章节的尾部,一方面是作为一个新的数学情境,再次吸引学生的兴趣,让学生运用垂直平分线作图的知识解决新的问题;另一方面与初始的寻找宝藏的情境相呼应.在线索文件中,宝藏在直线①②③相交而成的三个点所在圆的圆心上.因此该活动结束之后,学生即可用所学知识解决尺规作图章节之初的寻宝问题,这在一定程度上调动了学生继续学习的积极性.
4 思考与启示
总的来说,日本初中教科书平面几何章节中尺规作图出现的顺序明显靠前,这主要是受《要领》的影响.教科书对于尺规作图的编排呈现三大特点:一是设置“小学学习准备”栏目,加强初中与小学知识的衔接.二是设置有趣的情境,以作图为线索串联几何知识,吸引学生的兴趣.三是给出了作图的思考方式,而不是直接给出作法. 在此基础上,可以对我国初中数学课程标准与教科书的编写提出建议.
4.1 将尺规作图内容前置,作为认识图形、理解几何概念的工具
将《课标》中尺规作图内容前置,把尺规作图作为初中生几何学习初期认识几何的工具.通过尺规作图,学生经历“构造”平面几何概念的过程,以形成对几何概念与性质的直观理解.例如,在七年级认识三角形初期利用尺规作图,将圆规作为固定边长的工具,探索三角形三边的关系.仅仅需要图7这样一个特例即可形成对三角形“任意两边之和大于第三边”这一关系的直观理解.

图7 利用尺规作图探索三角形三边关系
4.2 强调尺规作图的思考方式,适当降低作法的要求
教科书可以通过设置备注、阅读栏目等方式,增加作图的思考方式、该作法的起源、还有哪些其他作法等内容.尺规作图与《几何原本》密切相关,以配图的形式增设《几何原本》中有关尺规作图的内容,可以让学生感受到尺规作图悠久的历史与价值,增加教材的人文感.
4.3 设计有趣的情境,应用尺规作图解决问题
针对我国教科书尺规作图零散分布于各平面几何章节的情况[4],一方面,可以在包含尺规作图的章节之初设计有趣的问题情境,在学习了该章节知识之后,回头解决一开始的问题,实现首尾呼应;另一方面,在学习完所有平面几何知识之后,设置一个综合性的数学情境,用尺规作图串联平面几何的知识,在解决问题的过程中促进各知识的理解与迁移.

