基本不等式的配凑技巧
2022-02-25 02:52朱东海
数理化解题研究 2022年1期
朱东海
(云南省蒙自市蒙自第一高级中学 661119)
1 拆项与添项
就是在保证正数和相等的前提下,通过拆项与添项配出定值.
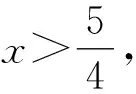
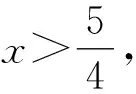

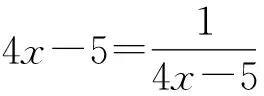

有的时候需要对给出的式子变形后,才能看出怎样配凑.

解析由已知,得
a2+ab+bc+ac=a(a+b)+c(a+b)
=(a+b)(a+c)

所以3a+b+2c=(a+b)+(2a+2c)
当且仅当a+b=2a+2c时等号成立.

2 乘方与开方
对有些无理式问题,可以先化为有理式,然后再配凑.
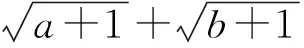

≤(a+1)+(b+1)+(a+1)+(b+1)
=2(a+b+2)=8,
当且仅当a=b=1时取等号.
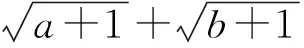
3 配系数
配系数的目的是为了配出定值.


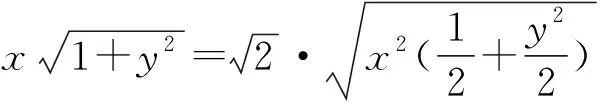
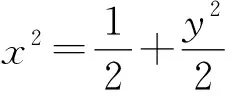


4 部分代入法
对某些二元函数的条件最值问题,可以用一个变量来表示另一个变量,代入目标式子,从而变为一个变量的问题.
例5已知x>1,y<0,且3y(1-x)=x+8,求x-3y的最小值.
解析因为3y(1-x)=x+8,



所以x-3y的最小值为8.
5 整体代入
就是把已知的式子或变形后代入目标式子,从而配出定值.


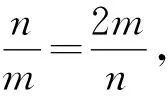
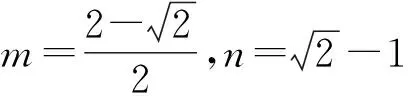

有时候需要先把式子变形后再代入.
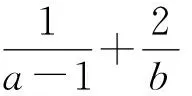
解析由a>1,b>0,若a+b=2,得(a-1)+b=1.

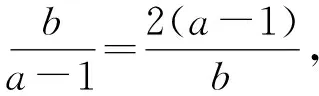
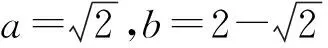
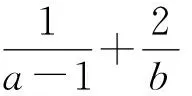
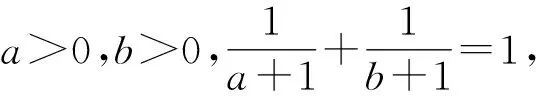
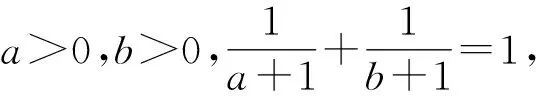
所以a+2b=(a+1)+2(b+1)-3

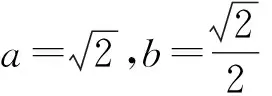

6 整体解出
就是把目标式子看成一个整体,利用基本不等式构造出新的不等式,然后通过解这个不等式求解.
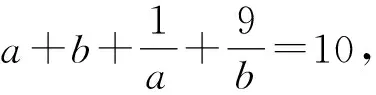



≥k2+6+10.
解得2≤k≤8.
故a+b的取值范围是[2,8].
7 利用等号成立的条件
若不能直接取等号,则可以利用等号成立的条件来拆分式子,满足等号成立.
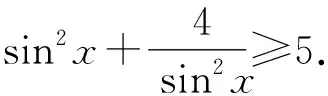

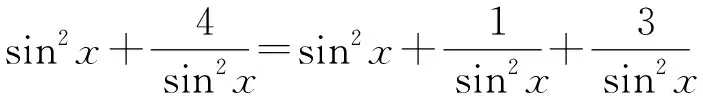
当且仅当sin2x=1时取等号.
注意两次放缩后必须每一次取等号的条件一样,最后等号才能成立.
8 多次应用基本不等式
有时候需要多次应用基本不等式才能求解.

解析因为a,b都为正实数,
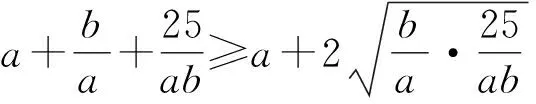
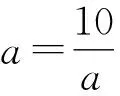
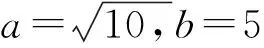
猜你喜欢
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
小猕猴智力画刊(2021年11期)2021-11-28
新世纪智能(教师)(2021年2期)2021-11-05
河北理科教学研究(2020年1期)2020-07-24
云南农业(2020年4期)2020-05-16
中国篆刻(2019年2期)2019-02-25
电子制作(2018年10期)2018-08-04
电子制作(2018年12期)2018-08-01
新高考·高二数学(2017年6期)2018-03-29
陶瓷(2013年11期)2013-11-26

