Regarding Deeper Properties of the Fractional Order Kundu-Eckhaus Equation and Massive Thirring Model

Yaya Wang,P.Veeresha,D.G.Prakasha,Haci Mehmet Baskonusand Wei Gao

1Department of Information Engineering,Binzhou Polytechnic,Binzhou,256603,China

2Centre for Mathematical Needs,Department of Mathematics,CHRIST(Deemed to be University),Bengaluru,560029,India

3Department of Mathematics,Davangere University,Shivagangothri,Davangere,577007,India

4Department of Mathematics and Science Education,Faculty of Education,Harran University,Sanliurfa,63050,Turkey

5School of Information Science and Technology,Yunnan Normal University,Kunming,650500,China

ABSTRACT In this paper,the fractional natural decomposition method(FNDM)is employed to find the solution for the Kundu-Eckhaus equation and coupled fractional differential equations describing the massive Thirring model.The massive Thirring model consists of a system of two nonlinear complex differential equations,and it plays a dynamic role in quantum field theory.The fractional derivative is considered in the Caputo sense,and the projected algorithm is a graceful mixture of Adomian decomposition scheme with natural transform technique.In order to illustrate and validate the efficiency of the future technique,we analyzed projected phenomena in terms of fractional order.Moreover,the behaviour of the obtained solution has been captured for diverse fractional order.The obtained results elucidate that the projected technique is easy to implement and very effective to analyze the behaviour of complex nonlinear differential equations of fractional order arising in the connected areas of science and engineering.

KEYWORDS Fractional Kundu-Eckhaus equation;fractional natural decomposition method;fractional massive Thirring model;numerical method;Caputo fractional derivative

1 Introduction

The study of complex models that exemplify the nonlinear phenomena and analyze their behaviour is essential and pivotal in the research of the present era.Particularly,the role of mathematics is significant to illustrate their nature with respect to time and other dependent parameters.The essence of calculus and its applications have become a hot topic from the beginning of its birth to till date.Since it is only instrument which can effectively and accurately predict the behaviour of the process raised in nature as a problem for living beings or solutions for the same.Recently,many pioneers and young researchers pointed out some limitations while designing or modelling complicated phenomena with classical calculus.Specifically, while examining hereditary properties,history-based mechanisms,non-Morkian processes,long-range propagations and others.Meanwhile,on the other hand the concept of calculus with non-integer order is rooted soon after the classical one in the process of the letter exchange between two great mathematicians.During the seventeenth and eighteenth centuries,this concept was not gets attracted by numerous scholars due to the unfamiliarity of its essence and associated applications in comparison with classical concepts.But, recently, due to the above cited boundaries of integer order calculus and revolution in the computational tools,the concept of fractional calculus (FC) fascinates many physicists, engineers and most importantly,mathematicians to develop the essential theory and corresponding computational tools deal with the real-world problem for the betterment of lifestyle of the human beings.Many senior scholars provided the base for the FC in order to understand in scientific needs of implementing this concept into reality[1-6].

Recently, many existed models have been examined by researchers [7-10].For instance, the new wave behavior of the equations exemplifying the phenomena associated with plasma physics is derived by researchers in [11], the scholars in [12] derived stimulating results associated with a numerical method for coupled KdV equations.The efficient approach is employed in [13] to model for thermostats with hybrid boundary value conditions,the reliability of the method is illustrated by researchers in[14]with respect to the(2+1)-dimensional Ablowitz-Kaup-Newell-Segur equation,the prey models with mutualistic predation is analyzed in[15]with the help of non-local and non-singular kernels.In a similar manner, the authors in [16-18] derived some interesting results associated with numerical methods.Moreover, the authors in [19] investigated the model that exemplifies the windinfluenced projectile motion within the frame of fractional calculus.In [20], researchers illustrated the impact of the generalization of the classical model with arbitrary models.These studies motivate us to investigate more complex models with the help of efficient numerical or analytical methods and aid us in investigating comparative numerical study.On the other hand, the following recent research work helps us to understand the essence of generalizing the concept with fractional order.For instance,the author in[21]derived the two Fibonacci operational matrix pseudo-spectral schemes to investigate the physical model, the researchers in [22] studied the SIR model of the current 2019-nCoV with Caputo operator,the complex nature of the Gross-Pitaevskii equations derived with the help of fractional derivative.Further,many scholars employed different fractional operators to analyze real-world problems and study the physical phenomena[23-28],for instance,COVID-19 in India[29],biological pest control in tea plants[30],and many others.

In the present investigation, the model exemplifying important phenomena in quantum field theory is considered.The nonlinear Schrödinger(NLS)equation plays a vivacious part in the study of nonlinear optics,photonics,quantum field theory,water wave,and others.Among such,the Kundu-Eckhaus (KE) equation and the massive Thirring model (MTM) are the most important models and describe the self-interactions of a Dirac field.In the 1980’s, Kundu [31] and Eckhaus et al.[32,33] proposed the Kundu-Eckhaus equation as a linearizable form of the NLS equation.Here,we considered the fractional Kundu-Eckhaus(FKE)equation and fractional massive Thirring model(FMTM).The fractional-order is presented to incorporate the memory consequences in the system,which aids in capturing the essential behaviour of the complex model as follows [34].The FKE equation

withu(x,0)=αeix.The FMTM equations are given by

withu(x,0)=αeixandv(x,0)=βeix.

whereu(x,t)andv(x,t)are the complex smooth envelop function of temporal(t)and spatial(x)variables,iis the imaginary numberandμis the arbitrary order.Authors in [35]illustrated that Kundu-Eckhaus and the complex Burgers equations are associated with a Miura transformation.The KE equation can effectively model the propagation of ultra short pulses in quantum and nonlinear optics,which can be employed to illustrate the optical properties of the fem to second lasers and helps to study the behaviour of different phenomena arising into chemistry.Further,the massive Thirring model(MTM)is the nonlinear complex system having two-component[36,37].This model is used to illustrate the propagation of optical pulse in nonlinear or periodic optical media.Much attention has been devoted to the connection between the quantum sine-Gordon model and the quantum Thirring model[38,39].This association helps the considered problem to describe the model either in accordance with perturbation theory or in accordance with ordinary perturbation theory for quantum solitons.

As much as real-world modelling problems are important,finding the solution for these models with differential equations is also important.With the help of literature,we can say that,every model does not process an exact solution.In this regard,researchers employed or aided by semi-analytical or numerical algorithms.In this connection,Adomian offered the Adomian decomposition method(ADM)[40],particularly to examine nonlinear systems.With the help of the Adomian polynomial,we can solve nonlinear terms in a simple form.Even though a wide community of researchers applied to study many physical and other problems,recently,many scholars showed that if this method is union with transformation leads the great efficiency accuracy and reduces time and computational work.To fulfil these necessities,Rawashdeh et al.proposed the FNDM[41,42],and it is a mixture of ADM and natural transform.From the lost three years,this projected scheme is applied by many researchers to examine many problems and systems[43-46].

The pivotal aim of the present work is to find a solution for the FKE equation and FMT model and study the behaviour of the obtained solutions with respect to fractional order.Since these equations play an important role in describing various complex phenomena, many authors find and analyzed the solution numerically as well as analytically.For instance, authors in [47] found the rogue-wave solutions in optical fiber for KE equation, and auxiliary equation expansion and modified unified algebraic techniques are considered in order to find the soliton solution for KE equation.Further,many efficient techniques are applied to analyze these equations, modified simple equation scheme[48], extended trial function method [49],q-homotopy analysis transform technique [39], and many techniques for KE and MTM equations having classical and fractional order derivatives[50-55].

2 Preliminaries

Here,we present the essential and basic notions of FC and natural transform.

Definition 1.The fractional order Riemann-Liouville integral of a functionf (t)∈Cδ(δ≥-1)is defined as

Definition 2.The fractional derivative in Caputo sense forf∈is presented as follows:

Definition 3.The Mittag-Leffler type function with one-parameter is defined[56]as follows:

Definition 4.The natural transform(NT)off(t)is symbolized by N[f (t)]fort∈R and presented with the NT variablessandωby[57]

Now,we present the NT for the Heaviside functionH(t)as follows:

Atω= 1,the forgoing relations signify Laplace transform and fors= 1 gives the condition for the Sumudu transform.

Theorem 1[58]: The NTRμ(s,ω)of the fractional derivative off (t)Riemann-Liouville sense is symbolized byDαf (t)and defined as

whereR(s,ω)is NT off (t),αis the order andnbe any positive integer.Further,n-1 ≤α ＜n.

Theorem 2[58]:The natural transformRμ(s,ω)of the arbitrary derivative in Caputo sense off (t)is symbolize bycDμf (t)and defined as

Remark 1:Basic properties of the NT are defined as follows:

3 Basic Solution Procedure of FNDM

Here,we consider the following coupled fractional system to demonstrate the solution procedure and the basic theory of the projected algorithm with linear(R)and nonlinear(F)differential operators

with initial conditions

whereDμu(x,t)andDμv(x,t)symbolize the Caputo fractional derivatives of theu(x,t)andv(x,t),respectively, andh1(x,t)andh2(x,t)are the source terms.On applying NT and with the help of Theorem 2,then Eq.(9)gives

On employing inverse NT on Eq.(11)to get

From given initial conditions,non-homogeneous terms,G(x,t)andH(x,t)are exists.The infinite series solution is present as

where theAnandBnare indicating the nonlinear terms ofFu(x,t)andFv(x,t),respectively.By using the Eqs.(12)and(13),we have

By the assist of Eq.(14),we obtain

Similarly,forn≥1 we can obtain the general recursive relation and defined as

Then,the approximate solutions are defined as follows:

4 Solution for Fractional KE Equation and FMT Model

Here,we consider the FKE equation and coupled fractional equations describing the MT model to illustrate the applicability efficiency of the projected method.

Application 4.1.Consider the FKE equation defined in Eq.(1):

associated to initial conditions

On simplification,Eq.(16)can be written as

By employingNTon Eq.(18),we have

The nonlinear operator is defined as

By using Eq.(17)in the above equation,we have

Employing inverseNTon Eq.(20),we have

By comparing both sides of Eq.(22)with the help of initial conditions defined in Eq.(17),we can easily generate the recursive relation as follows:

Continuing in the same procedure,we can achieve the remaining components ofun(n≥3).Then,we have

The exact solution for Eq.(16)with the initial condition considered in Eq.(17)atμ=1 is

Application 4.2.Consider the time-fractional coupled fractional equations describing the MT model[33]:

subjected to

On simplification,Eq.(25)can be written as

Now by performingNTon Eq.(27)to get

Then,we present the nonlinear operator as below:

The foregoing equation reduces on simplification as follows:

Apply inverse NT on Eq.(29),we have

The infinite series solution foru(x,t)andv(x,t)are respectively assume that

Thus, on comparing two sides of Eq.(31) and using conditions defined in Eq.(26), we can effortlessly get

Similarly,the remaining components ofunandvn(n≥3)can be achieved.Then,we establish the series solutions as follows:

5 Numerical Results and Discussion

Here, we find the solution for complex nonlinear problems arising in the quantum field theory using FNDM.To present the numerical analysis in terms of plots,we used MATHEMATICA 12.The nature of the imaginary part in contour plots and surfaces real part for the achieved results are drowned in Figs.1-3 with distinctμfor the FKE equation.The behaviour of FNDM result for Application 4.1 with different values of fractional order(μ)is cited in Fig.4.In order to elucidate the behaviour of coupled fractional nonlinear differential equations describing the massive Thirring model,we find the solution with the aid of FNDM.Particularly,the complexity associated with the model is quite high,and also essential to examine the capture of its physical interpretation with corresponding parameters.The nature of the imaginary part in contour plots and surfaces real part for the results obtained for the fractional-order MR model is plotted in Figs.5-7 with distinctμ(0.5,0.75 and 1).The nature of FNDM results for the real part for differentμare plotted in Fig.8.We can observe the projected system highly depends on the parameters accessible by the scheme and the fractional operator.More precisely, the nature of the imaginary part in the form of the counter plats can aid some simulating and exciting consequences.

Figure 1:(a)Behaviour for the real part(b)nature of obtained solution at t = 1(c)contour plot for the imaginary part of the FNDM results at α =1.3 and μ=0.5 for the FKE equation

Figure 2: (Continued)

Figure 2:(a)Behaviour for the real part(b)nature of obtained solution at t = 1(c)contour plot for the imaginary part of the FNDM results at α =1.3 and μ=0.75 for the FKE equation

Figure 3: (Continued)

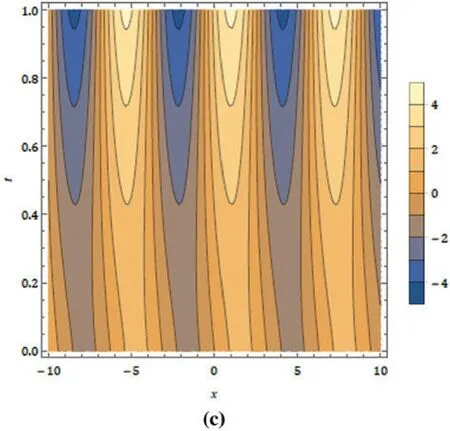
Figure 3:(a)Behaviour for the real part(b)nature of obtained solution at t = 1(c)contour plot for the imaginary part of the FNDM results at α =1.3 and μ=1 for the FKE equation

Figure 4:Response of the achieved result for the real part with distinct μ at α =1.3 and x=1 for the FKE equation

Figure 5: (Continued)

Figure 5: (a) Nature of the real part of u(x,t), (b) response of u(x,t) for the real part at t = 1, (c)contour plot of u(x,t),(d)surface of the real part of v(x,t),(e)nature of u(x,t)for the real part at t = 1,(f)contour plot of v(x,t)of the obtained solution for the FFMT model at α = 1,β = 1 and μ=0.5

Figure 6: (Continued)

Figure 6: (a) Nature of the real part of u(x,t), (b) response of u(x,t) at t = 1, (c) contour plot of u(x,t),(d)surface of the real part of v(x,t),(e)nature of u(x,t)for the real part at t=1,(f)contour plot of v(x,t)of the obtained solution for the FFMT model at α =1,β =1 and μ=0.75

Figure 7: (Continued)

Figure 7: (a) Surface of the real part of u(x,t), (b) response of u(x,t) for the real part at t = 1 (c)contour plot of u(x,t),(d)surface of the real part of v(x,t),(e)nature of u(x,t)for the real part at t = 1,(f)contour plot of v(x,t)of the obtained solution for the FFMT model at α = 1,β = 1 andμ=1

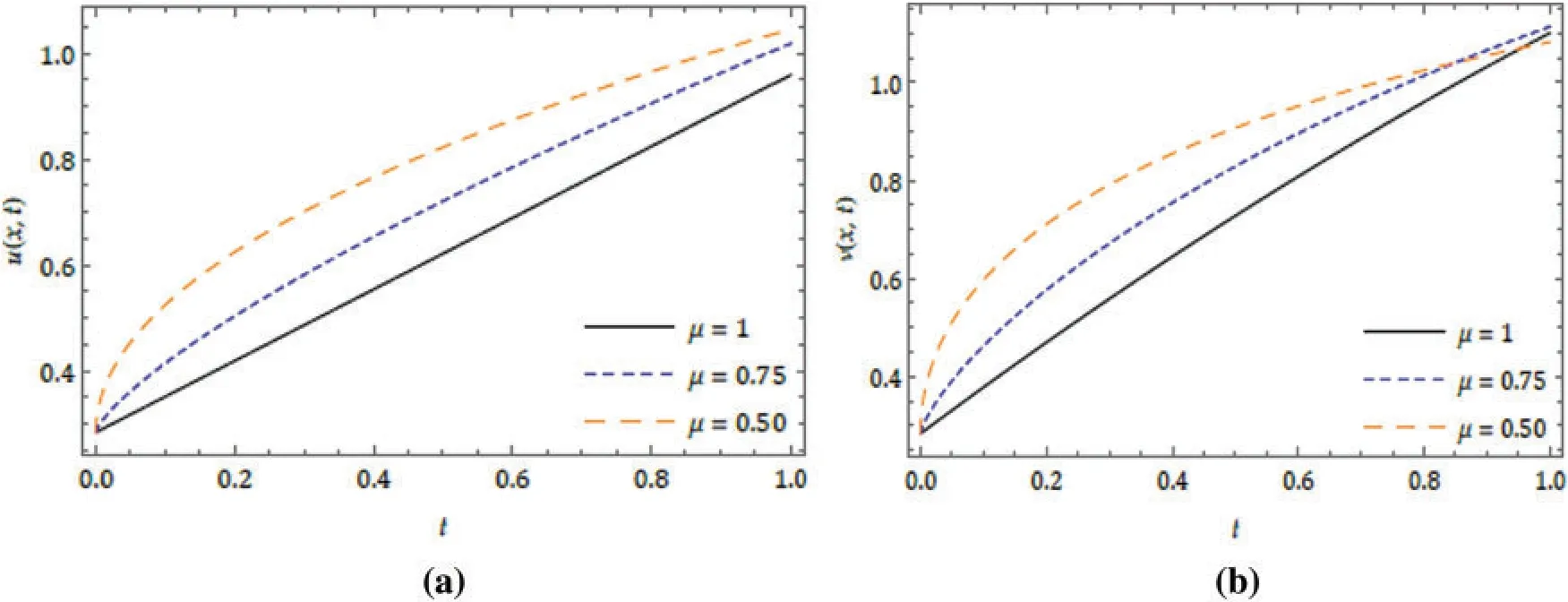
Figure 8:Nature of the real part of(a)u(x,t),(b)v(x,t)with distinct μ at α = 1,β = 1 and x = 5 for the FMT model

6 Conclusion

In this paper, we derived the solution for the projected nonlinear complex system exemplifying the fractional Kundu-Eckhaus equation and the massive Thirring model arising in the quantum field theory with the aid of FNDM.Particularly, counter and coupled surfaces are cited to understand more interesting consequences of the projected system.The novelty of the scheme considered is cleared dissipated to examine coupled systems, and by the projected solution procedure, we can find the solution for nonlinear models associated with complex functions without any dissertation and perturbation.The captured plots show the huge variations with a small change in the order of the system and it can help us to understand more consequences of the projected model.The considered system highly depends on time and analogous consequences with fractional order and it can observe by the present study and further,it can help to diverse classes of coupled nonlinear and complex differential equations.Finally,the results gained by the considered algorithm are interesting as compared to other available results,and hence it can be hired to analyze and examine the various complicated phenomenon.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.