基于Kriging和NSGA-III算法的汽车交流发电机温度场预测

黄燕， 李露， 蒋孝文， 董大伟， 马兴桥

(西南交通大学 机械工程学院，四川 成都 610036)

0 引 言

汽车发电机的散热问题一直得到工程界和学术界的关注，其温升特性直接影响到发电机的性能和汽车的安全性。汽车交流发电机在高转速下，发电机的各项损耗最终变成热能[1-2]，使其内部温度升高，过高的温度可能破坏发电机绕组表面绝缘层引起短路危险，也可能破坏铁心叠片间的绝缘层造成铁损增加，甚至带来轴承套热变形及机械强度降低等问题，增加设备工作的危险性。因此汽车交流发电机运行过程中温升的监测和研究就显得尤为重要。若能够提前预测发电机在某工况下各个部件的温度情况，就能有效防止因部件过热引起绝缘层失效、热应变等问题，提高其工作安全性。

电机温度场与电磁场、流场等物理场密切相关[3]，且电机由于内部部件紧凑，发热、流动散热特性较为复杂。目前常用的发电机温升计算方法有等效热网络法[4]和有限元法[5]。等效热网络法能较准确地得出电机温升分布，但其只能获得节点平均温升，相比之下，有限元方法求解温度场能够较为全面的获得温升及热点位置。SUN等[6]采用有限元软件计算铁心损耗并分析稳态下电机热分布，张琪等[7]对电机进行热场仿真分析的结果表明电机最高温度位于定子绕组端部，丁树业等[8]针对高速永磁同步电机，建立了整机求解域模型，揭示了整机的温升分布规律和电流变化特性。电机温度场的数值研究呈现着从二维分析到三维分析，从单一温度场分析到多物理场耦合分析的趋势[9-10]。但普遍认为有限元方法分析预测电机温度分布具有一定的局限性：如需要大量的计算资源，其精度取决于网格质量、材料特性和边界条件等[11]。因此部分学者通过试验测试方法研究电机的温升分布及特性，温威振[12]采用稳态温升试验法分析永磁同步电机温度场分布，Ning Y等[13]针对一种混合励磁同步电机，通过多次试验和数值模拟获取其内部热量分布及传递特性，刘平等[14]研究电机运转过程中信号注入的方法对温度估计和输出转矩脉动的影响。但是，实验的测量分析主要针对于已设计成品，在发电机的研发阶段需要耗费大量的制作样件，获得的数据只能用于分析当前样件，在后续的优化和持续改进中耗时较长。

目前，机器学习算法已在众多领域展开了研究，通过数据样本的学习来探索和预测复杂事件的潜在规律具有重要的学术价值。侯冶等[15]建立了列车牵引电机转速、电流与力矩等状态参数与电机某监测位置处温度之间的非线性自回归神经网络预警模型，全工况条件下电机温度的预测误差在5 ℃以内；岑岗等[16]针对永磁同步电机基于冷却液温度、电压、电流、转速等参数以定子温度为预测目标进行了近端策略优化和强化学习网络模型的分析。总体来看，基于优化算法和数据样本对发电机温度场分布进行准确度较高的预测的研究成果还比较缺乏，尤其是覆盖发电机不同产热部位、不同运行工况以及不同运行时长的温度场分布式预测。此类方法能够在发电机设计前期对各部件在不同工况下的温度分布情况进行一定程度的预测，同时也可在运行中实现对更高转速范围的温度预测，具有一定的可靠性、先验性和便捷性。基于此，本文拟开展基于遗传算法的汽车交流发电机温度场分布预测方法的研究。

本文首先采用流固耦合有限元计算法，得到汽车发电机工作时各部件的温度场分布，并进行试验验证。在此基础上利用Pareto多目标优化理论，基于Kriging代理模型提出一种汽车交流发电机温度场分布预测的方法，考虑将实际温度场参数和预测温度场参数的差异构成目标函数，通过非支配解排序遗传算法III型(non-dominated sorting genetic algorithm III，NSGA-III)优化算法搜索最适合的温度场参数来使目标函数达到最小值，以达到预测发电机在不同工况下各个测点温度幅值的目的。

1 汽车交流发电机温度场数值计算

1.1 建模及网格划分

采用的汽车交流发电机为电励磁有刷爪极发电机，由爪极、转子、定子、硅整流器、前后端盖、冷却风扇和皮带轮组成，如图1所示。该型汽车交流发电机为内置双风扇的冷却结构，采用强制风冷散热，将发电机产热经前后端盖耗散。发电机的额定转速为10 000 r/min，容量为1 900 W，发电机各部件材料视作材质均匀，各种材料特性汇总于表1所示。

图1 汽车交流发电机结构示意图Fig.1 Schematic diagram of automobile alternator structure

表1 交流发电机材料特性参数

利用计算流体力学(computational fluid dynamics，CFD)前处理软件Workbench-Mesh进行网格划分，采用四面体非结构网格方式，建立各计算域间节点共享的网格模型，如图2所示，网格经过无关性验证确定总数为793.5万，网格尺寸设置最大为1 mm，并对扇叶、端盖栅格等结构进行网格加密。

图2 汽车交流发电机网格模型Fig.2 Mesh model of automobile alternator

温度场数值模拟计算之前，需进行热源的确定，车用汽车交流发电机的热源主要由铁心损耗、绕组铜损耗、机械损耗和杂散损耗等组成。对于发电机来说，工作状态下铁心损耗与绕组铜损是发电机热源的主体部分，机械损耗和杂散损耗可以忽略不计。通过Maxwell有限元计算满负载转速10 000 r/min情况下的损耗及生热率如表2所示。

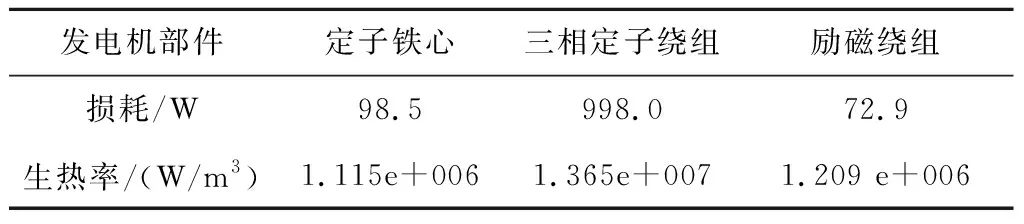
表2 交流发电机部件损耗及生热率

基于ANSYS通过流固耦合传热方法求解发电机在10 000 r/min下稳定运行时的温度特性，流体与固体交界面之间的对流换热由仿真软件耦合解析。稳态计算采用RNGk-ε湍流模型，并开启能量方程，采用Coupled算法，旋转流域运动方式设为Frame Motion，转速为10 000 r/min，计算至模型收敛。

1.2 温度场分析

图3为该型交流发电机在负载10 000 r/min稳定运行下端盖、转子以及定子的温度分布云图。从云图提取数可知，三相定子绕组的温度为397.81～407.99 K，定子铁心温度为365.67～393.95 K，发电机最高温度407.99 K出现在三相定子绕组端部，最低温度311.01 K出现在冷却扇叶上。这是因为三相定子绕组具有最高的热效率，并且围绕着一种具有较低的热传导率的物质，例如绝缘涂料、浸渍涂料和空气，发热较为严重。定子铁心的生热率低于定子绕组，因此，铁心中部和绕组端部存在一定的温度梯度，虽然端部更靠近发电机冷却风扇，但绕组上的最高温度仍出现于端部。另外，定子铁心齿顶靠近较薄的气隙层散热困难，而轭部靠近端盖散热相对容易，这也使定子铁心径向上由内向外温度逐渐降低，且绕组端部温度较高。

图3 发电机部分零部件温度云图Fig.3 Temperature contour map of parts of the alternator

发电机端盖的高温区分布在贴近铁心的部分，最高达379.52 K，且端盖温度在轴向呈现着“中间高两端低”的趋势，这一趋势与实际相符，也是热量大部分传导至端盖，从而引起端盖温度上升，而端盖的轴向两端设计有冷却空气流过，通过对流传热作用带走热量，使得温度低于端盖中间部分。

发电机转子的最高温度为336.07 K，其中励磁绕组的最高温度为327.27 K，爪极的最高温度为330.54 K，转子整体最低温度311.01 K，其中低温区为扇叶，而高温区为转子轴承部位，因为转子的热量来源主要有两个部分，其一为励磁绕组通电产生的热量，其次是定子产生并通过端盖传导的热量，因此转子轴承位置的温度较高。通过以上分析可知，对发电机进行温度场分布预测时重点关注的部位应是三相定子绕组、定子铁心和端盖。

2 汽车交流发电机温升的试验测试

本节通过在实验台架上对该发电机的重点温度管控部位进行温度测试，验证发电机温度分布数值仿真结果的正确性，同时取得对发电机温度场分布预测的数据样本。

2.1 试验测试平台简介

发电机工作在稳态负载工况下的温度测试试验步骤为：在实验室环境下，将发电机接入负载电路，设置控制台架驱动程序，使发电机均匀加速至10 000 r/min然后恒速运转，与此同时进行温度采集。

依据上述仿真计算结果，并综合考虑传感器安装的难易程度，热电偶布置在发电机端盖、槽外三相定子绕组以及定子铁心上，发电机温度最高的绕组端部区域，布置了多个传感器(1#、8#、10#、11#、12#)，具体位置如图4所示，试验所用仪器设备及其型号如表3所示。

表3 测试设备型号及参数

图4 热电偶安装位置示意图Fig.4 Schematic diagram of thermocouple installation positions

2.2 试验测试结果

图5示出了各热电偶测点温度随时间的变化过程，由图可知，发电机负载下工作的前期，在约120 s内温度迅速上升，恒定转速工作一段时间后，由于发电机的发热量和耗散热量基本达到了动态的平衡，发电机各个部件温度趋于稳定。其中槽外定子绕组部分的温度曲线达到峰值后，距离前后扇叶较近，温度有一定的下降最终趋于稳定。

图5 各测点温度随时间的变化Fig.5 Temperature variation with the time of measuring points

实验测试结果和仿真结果特性一致，表4为部分温度测点值与仿真温度值的对比，最大误差为3.01%。由表可知三相定子绕组(8#、10#、11#)温度较高，这对导体绝缘材料的耐热性要求极高；定子铁心(7#)温度也较高，将对定子铁心材料的磁导性能造成一定影响。同时由图5可知，汽车交流发电机120 s内的温度逐渐升到峰值。因此，基于这段时间内对该型发电机的温度场分布进行预测分析，以有效防止部件温度过高对电机结构、性能的影响甚至设备的破坏，需要指出的是，在发电机实际运行中应当对不限于120 s运行时段的温度场分布进行预测，文中所述算法对发电机长时间运行时的温度场预测同样可用。

表4 试验与仿真部分测点温度对比

3 NSGA-III和Kriging代理模型的构建

发电机的温度场分布预测问题可以等效为优化问题，因此考虑将实际温度场参数和预测温度场参数的差异构成目标函数，通过优化算法搜索最适合的温度场参数来使目标函数达到最小值，从而预测各个测点的温度幅值。在NSGA-III进行多目标优化的过程中，同时使用Kriging代理预测汽车交流发电机各测点温度分布。

3.1 Kriging代理模型的构建

首先采用Kriging代理模型构建交流发电机转速n、运行时间t与其各个部位温度T的关系，为后续的温度场预测建立基础。根据汽车发动机常用的转速情况，发电机转速范围选取为6 000～12 000 r/min，参考上述实验温度场测试结果运行时间范围为10～120 s。温度场测点如图4所示，测点数目为12。

基于12个测点在不同转速、不同时间段的温度值构建Kriging代理模型，相关函数选择EXP。使用拉丁超立方采样方法[17]生成初始转速、时间样本xi=(niti)，发电机温度场试验测试数据 (T1(xi)T2(xi)T3(xi) …Ts(xi))构建矩阵Y，即：

(1)

(2)

式中：xi=(niti)为第i个发电机运行工况样本，转速为ni，运行时间为ti；Y为当电机的运行工况为xi所测得的温度场分布情况。为使拟合的代理模型更加精确，将每个运行工况12个温度场测点分成两个部分表示为s1=7，s2=5。

3.2 多目标优化算法

多目标优化问题一般为多个目标函数在相应约束下同时优化的问题。其通常有多组最优解满足条件，从数学角度表示如下：

(3)

(4)

式中：Fm(u,x)为第m个优化目标函数，m为需要优化的目标函数数量；约束条件包括hj(u,x)=0等式约束和gj(u,x)≤0不等式约束；uimin和uimax分别为第i个控制变量的上下限，D为上限和下限约束的数量。

在多目标优化中，由于各个目标函数和约束条件的限制，往往其中一个目标函数优化效果的提升会引起其他目标优化效果的下降，要得到所有目标函数的最优解是很困难的。因此，一般多目标优化问题的解集通常为非劣解的解集，即Pareto最优解集[18]。多目标优化问题通常存在多个Pareto最优解集，没有其他条件限制很难选择最优解，可以认为多目标优化的重要目标是寻求该优化问题的尽可能多的Pareto最优解。传统的优化算法主要存在两个弊端：对Pareto最优解形状敏感，一个目标函数支配其他目标函数[19]，所以对使用范围有特定的要求。文中采用的NSGA-III[20-21]有效避免了以上问题，当目标函数个数大于4个时，NSGA-III算法可以有较好的优化效果，并能够很好地处理更多个目标的优化问题。

在利用NSGA-III进行多目标优化前，需要构建目标函数，交流发电机温度场预测问题可以转化为：

findx*={n*,t*}；

(5)

(6)

约束条件：

(7)

式中：Ts(x*)为通过Kriging代理模型预测得到的温度场幅值；Ts(xTarget)在试验中测得的温度场数值，其中s分为两组s1=7，s2=5。

基于代理模型和NSGA-III的交流电机温度场预测步骤如图6所示。经过NSGA-III种群的变异迭代，最终优化得到一系列Pareto最优解，最后一个子代所有的参数使所有的目标函数达到最小，采用适当的评价指标在Pareto最优解选择一组最佳温度场幅值。即在优化过程中目标函数达到最小值时可认为此时的温度场测点温度即为预测的温度场幅值。

图6 基于代理模型和NSGA-III的电机温度场分布预测流程图Fig.6 Predicting process of temperature field distribution for the alternator based on surrogate model and NSGA-III algorithm

在图6中定义Mobw为温度分布幅值最终选择指标，Mobw是对每一个子代的目标函数值进行加权的总和，Mobw的最小值所对应的个体为最终选择的温度幅值，即

(8)

式中：ki为权重系数；Object(i)为每一个子代的目标函数值。

4 温度场分布预测分析

基于以上Kriging代理模型方法和NSGA-III多目标遗传算法，本节首先使用拉丁超立方取样生成50组电机运行工况进行试验测试作为数据样本，然后利用基于Kriging代理模型构建发电机转速及运行时间和温度分布幅值的关系，并进行NSGA-III多目标函数优化。为防止算法迭代优化过程中陷入局部最优，经多次遗传算法测试，初始参数选择如下：种群规模为80，交叉概率为0.5%，变异概率为0.5%。

抽取数据样本其中5组(如表5所示)温度分布预测的代表性工况来进行预测算法有效性的分析。图7为第一组电机运行工况[8 046.1 r/min，114.2 s]采用NSGA-III算法进行优化过程中适应值的收敛情况，可以看出在进化代数大于40时目标函数值基本收敛。

图7 第一组运行工况适应值随进化代数变换情况Fig.7 Adaptive values of the first group of operating conditions with evolution algebras

表5 汽车交流发电机部分试验工况(验证样本)

文中主要研究发电机端盖、槽外三相定子绕组以及定子铁心等部位的温度分布，因此选取测点3、测点5、测点7、测点8、测点10、测点11进行预测结果分析。图8为采用NSGA-III算法优化的代理模型后电机端盖部位温度分布的预测结果和实测结果的对比，测点3温度值预测结果在362.0～363.8 K范围内，实际温度值为364.0 K，最大误差为0.55%，其中预测误差最大是测点5，误差值为3.05%。

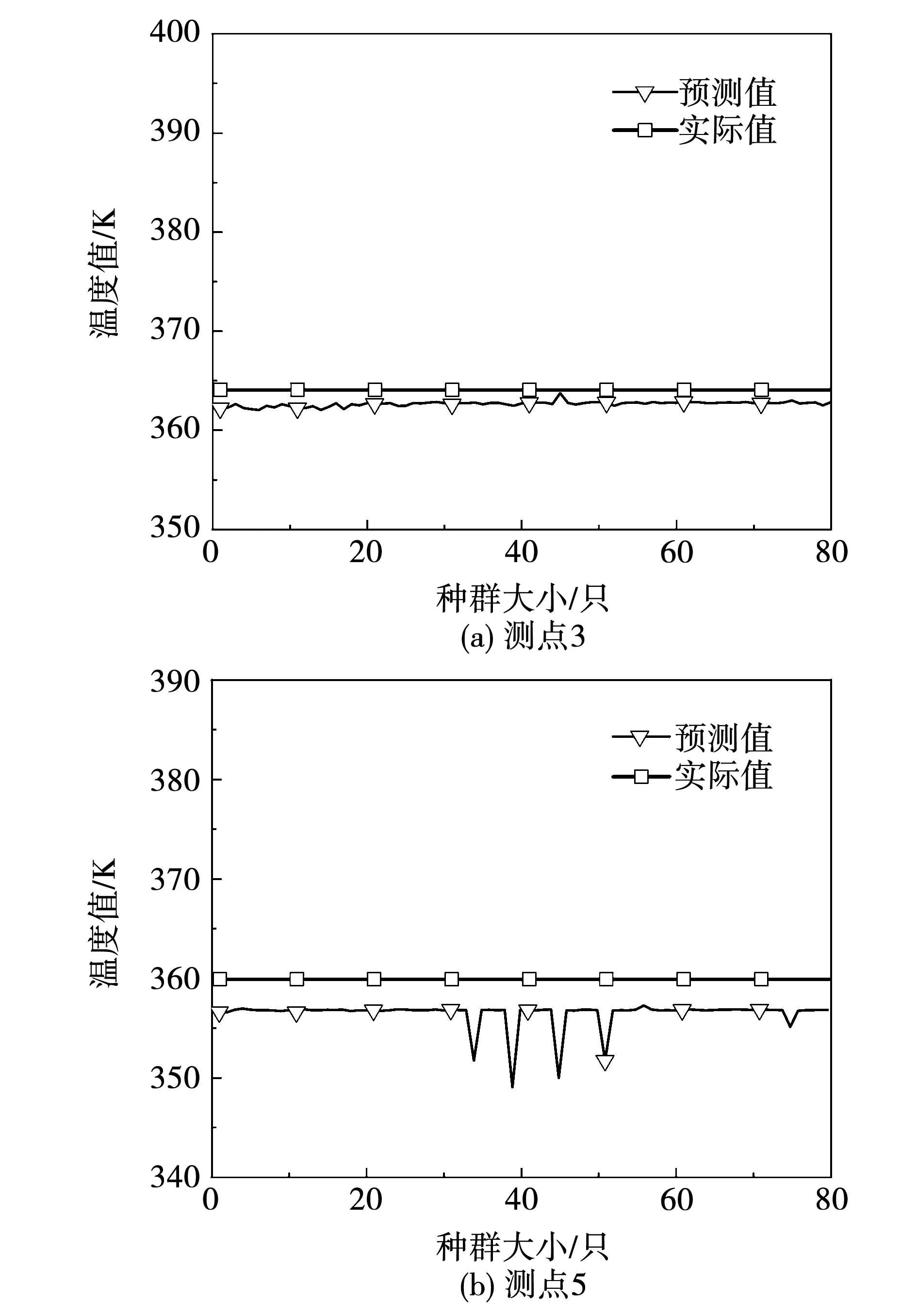
图8 最终种群中个体的温度分布值(端盖部位)Fig.8 Temperature distribution of individuals in the final generation at end cover

三相定子绕组是本实验中温度最高的区域，达到了423.3 K。若电机长时间运行在此温度下，将会破坏绕组表面绝缘层引起短路危险，所以能否有效及精确地预测此区域的温度分布是重点研究目标。

图9和图10为定子铁心和定子绕组部位预测值和实测值的对比，由图可知温度预测值随着种群数量增长略微波动，当种群数量繁衍到一定程度之后，预测值基本保持水平。由于种群数量增加之后，算法运行的成本会随之成倍增长，所以综合考虑选取的种群数量为80。每个工况预测程序平均运行时长为96 s，同比数值仿真和试验测试耗费时间更少。同时从图中可以看到，在对目标函数优化过程中，部分测点预测值较实际值高，部分测点预测值较实际值低，但图中呈现出的预测值和实际值的相对波动对整体预测结果和预测的精确度影响不大，这与算法固有的择优生成并选择子代传递的稳定性有关，基于当前的参数和限制条件设置已具有较高的精确度，其中定子部位的预测精度较高，平均误差为1.02%，定子绕组部位的3个测点预测误差最大误差为0.49%。因此，提出的Kriging代理模型和NSGA-III优化算法的结合在交流电机温度场分布预测方面具有有效性和精确性。

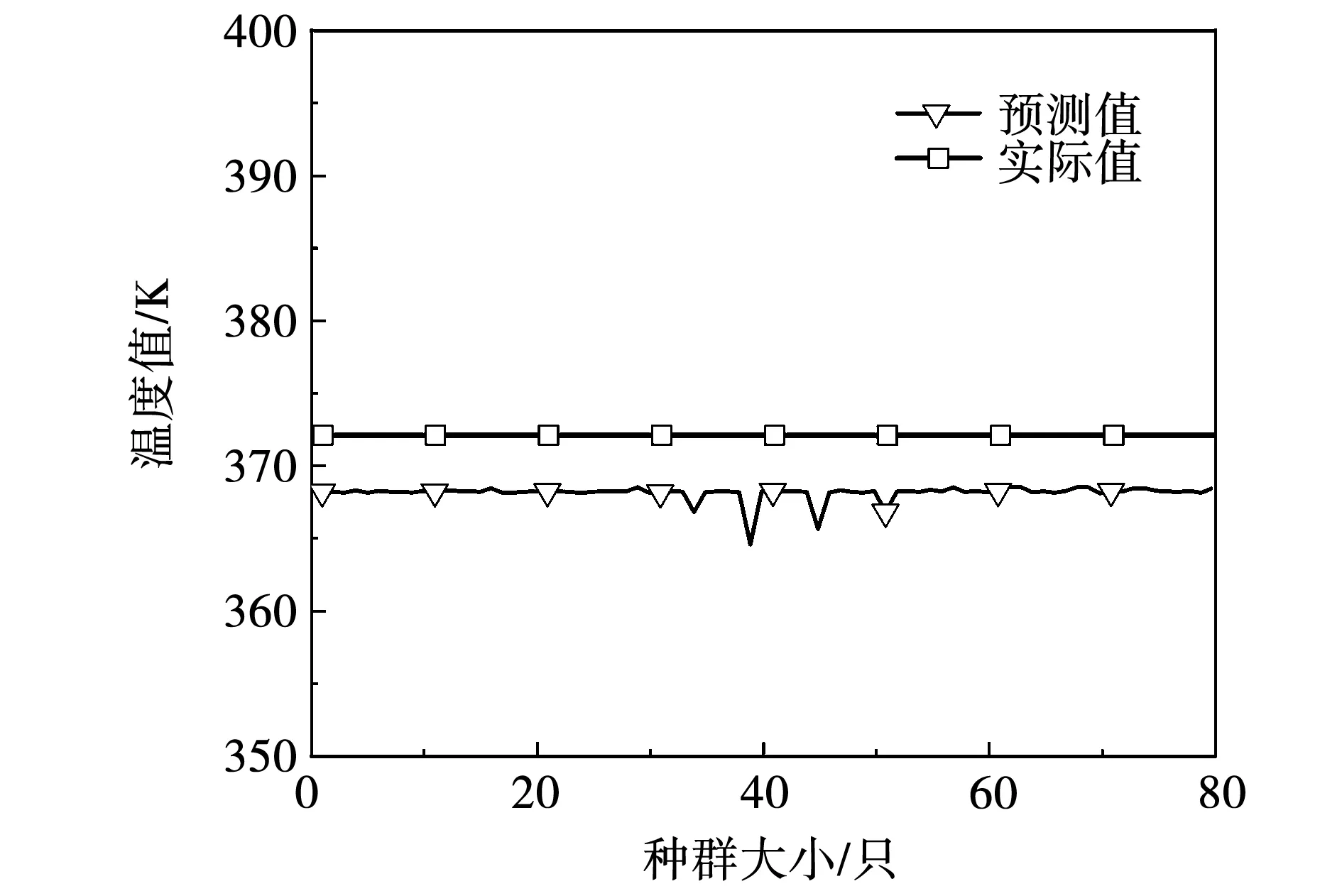
图9 最终种群中个体的温度分布值(定子铁心测点7)Fig.9 Temperature distribution of individuals in the final generation atmeasuring point 7 of stator core

图10 最终种群中个体的温度分布值(定子绕组)Fig.10 Temperature distribution of individuals in the final generation at stator winding

在预测过程中只需要确定一组温度分布值作为预测的结果，但是实际中并不存在一组温度值使得所有的目标函数值都取得最小，因此根据式(8)中Mobw选择指标在Pareto最优解集中选取最佳的温度分布值，使预测结果误差达到最小，更加接近实际温度值。

图11为在Pareto最优解集中得到的种群中所有预测结果的值，图中可以看出在第52组解集中取得最小值，因此将Pareto最优解集中第52组作为最终预测的温度场分布。另外四组工况也采用同样的评价指标，选择出最佳温度场幅值。

图11 温度场预测结果评价指标Fig.11 Evaluation index of temperature results

满足Mobw值选择指标后的部分预测结果如表6所示，为第一组工况[8 046.1 r/min，114.2 s]下的所有测点位置的温度对比。由于第一组工况的运行转速和运行时间都较大，发电机各个区域的温度都较高，实测温度和预测温度的最小误差为0.02%，最大误差为1.05%。其中温度较高的测点，特别是处于绕组端部附近的测点(如测点1、8、10、11、12)，其预测误差相比于其他区域较低，而区域的温度越低，预测误差越大，这是因为高温区域的样本点越多，拟合的Kriging代理模型在高温区域的精度就越高；同时高温测点的温度幅值远离NGSA-III算法中的优化边界，而低温测点的幅值在边界附近，寻优精度较高温区略低，但整体预测温差均在较低范围内。综上分析，本方法能对发电机在高速、长时间运行工况下的高温区域的预测具有较好的有效性与准确性。

表6 发电机温度场分布预测结果(第一组)

对于每一组工况下的所有测点的预测精度，使用MAPE[22]分析预测温度与实际值的误差，即

(9)

式中n为测点总数目12。

计算得到的各验证样本的温度场MAPE预测误差如图12所示，可以看出第一组工况的预测精度最高，MAPE值为0.53%；第二组分布预测结果中预测误差稍有偏大，MAPE值为2.78%，这是因为第二组电机运行工况[10 926.4 r/min,12.1 s]已经非常接近构建Kriging代理模型的边界条件，即转速接近最大极限12 000 r/min，运行时间接近最小时间10 s。如果在构建Kriging代理模型时加大样本数量，同时增加边界运行工况的样本，可以进一步提高此类运行工况温度场分布预测的精度。

图12 验证样本组温度场的MAPE预测误差Fig.12 MAPE prediction error for temperature field of verification sample set

基于以上分析，可以看出所述方法能够对发电机不同转速和不同运行时长下不同部位的温度场分布进行具有一定精度的预测，与仿真计算相比，耗时较少，且与试验数据误差更小。

5 结 论

本文通过ANSYS进行流固耦合有限元仿真计算及试验测试，分析了汽车交流发电机工作时部件的温度场分布情况，并结合Kriging代理模型和NSGA-III优化算法构建了交流电机温度场预测的多目标程序，主要结论如下：

1)发电机在10 000 r/min下稳定运行时，整机最高温度位于三相定子绕组上，最低温区域出现在冷却扇叶。其中发电机端盖的高温区分布在贴近铁心的部分，在轴向呈现着“中间高两端低”的趋势；转子整体最低温度311.01 K，其中低温区为扇叶，而高温区为转子轴承部位。发电机稳态温升的试验验证了发电机温度分布数值仿真结果的正确性，测点温度的最大误差为3.01%。

2)基于Kriging和 NSGA-III优化算法预测的发电机在不同转速和运行时间下各部件的温度分布具有可行性和准确性，最小预测误差为0.53%；对于处于代理模型边界条件附近的运行工况，预测误差稍有增大，最大为2.78%。本文所述方法对于发电机在设计前期和高速、长时间运行状态下的温度场分布预测具有高度的有效性与精确性以及便捷性。