完美平顶涡旋光束

姜嘉琪,Carmelo Rosales-Guzmán,朱智涵

(哈尔滨理工大学,黑龙江省量子调控重点实验室,大珩协同创新中心,黑龙江 哈尔滨 150080)

0 引言

1992年,Allen等[1]证实了轨道角动量(OAM)的存在,携带OAM的各类“涡旋”光束立刻引起了光学界的研究兴趣。这些涡旋光束包括拉盖尔-高斯(LG)光束、合流超几何(HyGG)光束、完美涡旋光束等[2−4]。携带涡旋相位结构这一特殊性质使其在光学微操控、非线性成像、螺旋相衬等领域具有重要潜在应用,因此成为光场调控研究的重点关注对象[5−7]。近年来,随着研究的深入,涡旋光束的产生、调控及表征研究的焦点已从“相位结构”向“可定制”的空间复振幅结构转移,特别是在涉及光与物质相互作用、非线性光学等领域。其中,在高维结构光场非线性频率及OAM变换、上转换边缘成像等技术中,都需要“纯净涡旋相位结构”的OAM光-物传输。这需要一种具有均一空间振幅分布且无全局曲率相位梯度的“完美平顶涡旋”光束。

本文从理论出发提出了完美平顶(或称超高斯)涡旋光束的概念,并给出基于复振幅计算全息技术[8]的产生与调控方法。介绍了在傅里叶变换系统中产生、调控完美平顶(及平顶涡旋)光束的实验方法及装置。重点阐述了在给定孔径限制条件下获取光滑涡旋奇点的强度控制原理及方法。

1 原理及方法

平顶光束指的是在光束横截面上具有均一光强及相位分布的一类傍轴光束,其在数学形式上可用超高斯(SG)分布描述[9,10]。在柱坐标系{r,φ,z}中,其在束腰平面z=z0处的复振幅ESG(r,φ,z0)可表述为

式中:w为光束束腰半径,k为波矢量,正整数n(n≥2)则被称为超高斯分布的阶数。通常n=2时,光束横向分布为常见的高斯分布;而当n>2时,即为平顶光束,且n越大,光束横截面的平整性越好。图1所示为w=1 mm的几种不同阶数超高斯模式的横向分布对比,选取n=12超高斯模式分布作为目标光强分布。

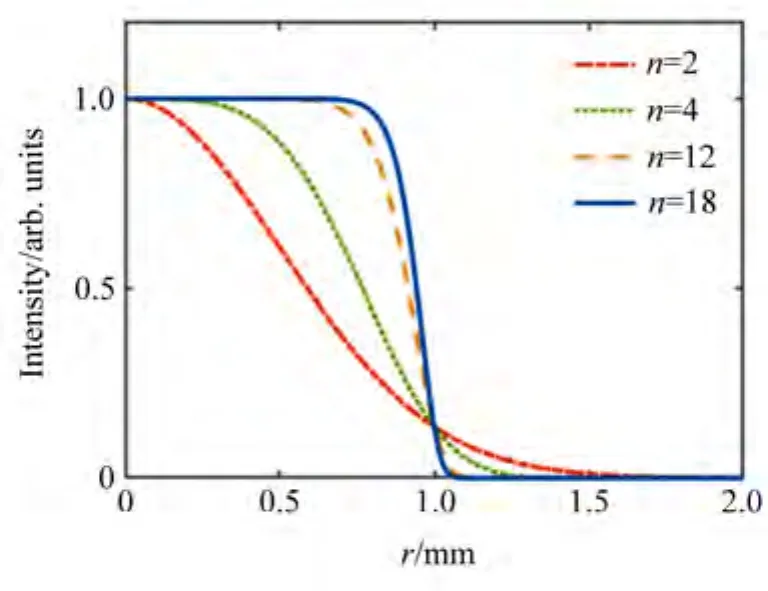
图1 不同阶数超高斯模式横向强度分布Fig.1 Transverse profiles of super-Gaussian modes with different order n

在此基础上,平顶涡旋可表示为携带螺旋相位因子ϕOAM=exp(iℓφ)的超高斯涡旋(SGV)光束,即

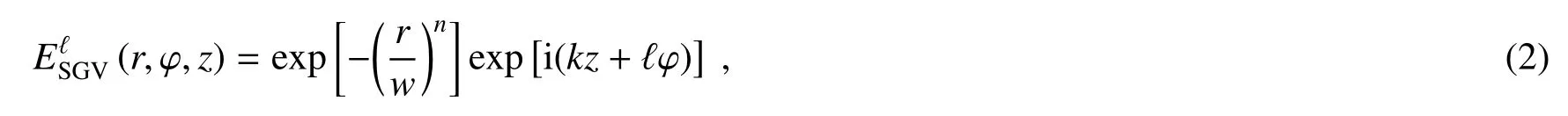
式中ℓ为涡旋相位的拓扑荷。特别地,当ℓ=0时,该光束变为(1)式中的SG光束。需要指出的是(2)式所示光束并非傍轴波动方程的本征解,但可表述为具有全同拓扑荷、不同径向指数p的LG模式叠加态

式中ap(z)为LG模式叠加的权重。根据LG模式Gouy phase与模态阶次(N=2p+|ℓ|)的关系可知该光束的空间结构与HyGG模式类似,随传播发生改变且p模式高频成分随|ℓ|快速增加[11]。下面选取ℓ=0,1,2且w=1 mm的SGV光束作为具体示例进一步论证,其光强与相位分布如图2(a)所示。经过一次傅里叶变换后,其傅里叶光场复振幅可表示为

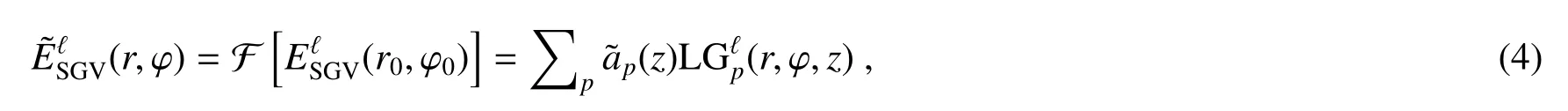
图2 (a)ℓ=0,1,2的SGV光束的空间光强及相位分布;(b)相应傅里叶光场的空间光强及相位分布Fig.2 (a)Spatial intensity and phase distribution of the SGV beams with ℓ=0,1,2;(b)Corresponding intensity and phase distribution of their Fourier transform

下面根据上述理论介绍如何利用相位型空间光调制器(SLM)产生目标SGV光束(也可使用几何相位液晶光学元件对光束进行调控产生[12,13])。总体思路是:计算目标SGV光束的傅里叶光场空间复振幅利用复振幅调制技术在SLM表面产生该光场[8],最后在傅里叶透镜焦平面产生目标SGV光场。利用相位型空间光调制器实施复振幅调制的关键是利用闪耀光栅效率实现空间强度(或振幅)的控制。在平面波入射条件下,闪耀光栅衍射效率ηeff(r,φ)与目标光场归一化空间光强IT(r,φ)=|ET(r,φ)|2一致,其中ET(r,φ)为目标光场空间振幅,即IT(r,φ)= ηeff(r,φ),所以闪耀光栅相位深度调制因子M(r,φ)与目标光场归一化空间光强分布的关系为

将(5)式作为强度掩膜与目标光场相位信息叠加,即可得到平面波入射条件下的全息复振幅掩膜

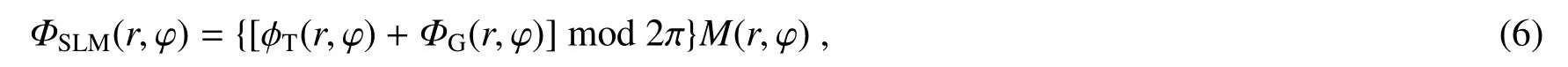
式中:ϕT(r,φ)为目标光场的相位分布,ΦG(r,φ)为闪耀光栅相位分布,AmodB表示取A除以B的余数。

式中Iin(r,φ)为高斯照明光的光强分布。由(5)式与(7)式可得到高斯光束作为照明光时的光栅深度调制因子

最终,根据高斯照明修正后的复振幅掩膜可表示为

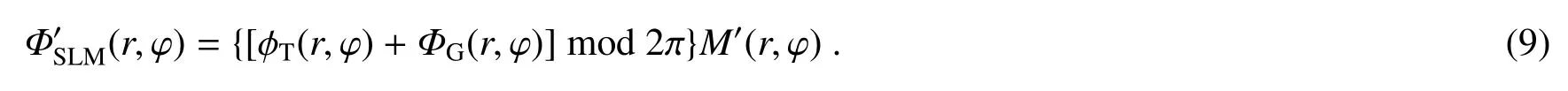
基于以上理论,便可由目标光场复振幅计算得到其相应复振幅掩膜。图3(b)展示了在高斯照明光条件下制备修正用于产生的复振幅掩膜全息图。需要注意的是,通常修正因子追求对照明光的最大利用率,但应保证目标光场的强度包络不超过照明光束的高斯形强度包络,以防制备光场模式畸变。

图3 产生的复振幅掩膜制备流程。其中(a)、(b)分别为高斯照明修正前后的复振幅掩膜Fig.3Preparation of the complex-amplitude mask for generating,where(a)and(b)are complex-amplitude masks before and after the amendment for Gaussian-beam illimitation,respectively

需要注意的是,除上述照明修正外,还需考虑用于产生SGV光束的实际光学系统口径对高频信息的衍射限制。因为当ℓ>0时,(3)式中的LG径向频谱是无穷级数,且高频分量占比随ℓ递增。下面结合实验系统做具体分析。图4(a)所示为实验装置图,其核心部件包括相位型空间光调制器(SLM)以及焦距为f=200 mm的傅里叶透镜(FT lens)。仿真及实验中采用λ=780 nm的TEM00模式单频激光作为照明,目标焦场平顶束腰设为w0=0.39 mm(对应傅里叶平面光束束腰为wf=λf/πw0=0.13 mm)。衍射限制(硬边)光阑半径设为5 mm。图4(b)为仿真及实验观测到的焦场SGV光束,仿真数据精确预测了实验结果,特别是ℓ≠0时相位奇点周围的能量干涉震荡。该震荡是由于当ℓ≠0时,(3)式高频分量(高阶p模式)将显著增加,高频分量通过硬边光阑(剪切强度调制)时将产生新生低频组份,并与原有相应低频组份在光束中心附近发生模间干涉进而产生径向条纹。

式中的超高斯阶数选取原则是让频谱主级区域(频谱中心主环)高比例通过,以保证构造SGV光束整体形貌的LG频谱低频组分尽量保留。如图4(c1)、(d1)所示,本实验针对ℓ=1,2的SGV光束分别选取了n=2.8和n=3.5的超高斯函数作为低通滤波函数;图4(c2)、(d2)为相应LG频谱在滤波前后的分布对比;图4(c3)、(d3)为最终制备出的SGV光束在焦场区域的强度分布。实验观测结果与理论高度吻合,产生的SGV光束具有完美的超高斯平顶强度,同时具有平滑的中心奇点及光束边缘强度分布。

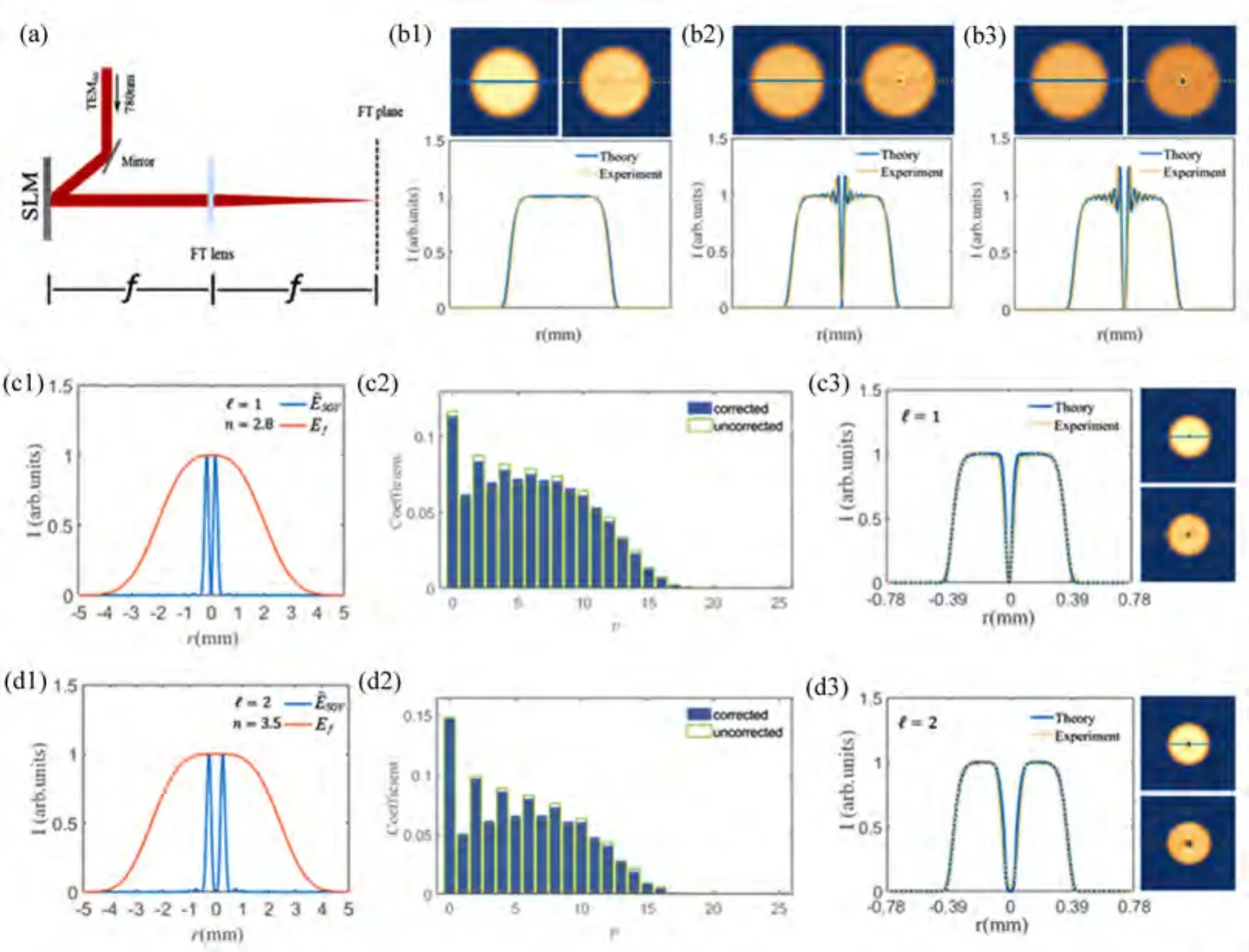
图4 (a)实验装置原理图;(b1)∼(b3)无低通滤波时的焦场SGV光强分布;(c1)∼(c3)及(d1)∼(d3)加入低通滤波后的理论及实验结果Fig.4 (a)Schematic of the experimental setup;(b1)∼(b3)Simulated and observed beam profiles of SGV beams without low-pass filtering;Data in(c1)∼(c3)and(d1)∼(d3)are results obtained by using low-pass filtering

2 结论与展望

通过理论结合实验,系统论述了如何基于复振幅计算全息技术在焦场获得具有均匀光强与平整相位分布的SGV光束;重点论证了如何克服实际系统孔径边缘截止高频信息导致的光束奇点处径向光强震荡问题。所论述的SGV光束为基于光与物质相互作用过程的相关应用及基础研究领域提供了重要手段。对于线性系统,能在光镊系统中产生平坦宽厚的涡旋势垒;对于非线性系统,SGV光束能够在非线性介质中产生高峰值功率的涡旋平顶泵浦光场。基于所论述的SGV光束,本研究组将在近期报道模式无关的非线性OAM模式变换与探测,以及任意矢量光场的非线性产生。