轨道角动量光束非线性转换研究进展

周志远,史保森

(中国科学技术大学,中国科学院量子信息重点实验室,安徽 合肥 230026)

0 引言

1961年在石英晶体中观察到二次谐波标志着非线性光学的诞生[1],非线性光学的诞生给光物理与光学技术带来了巨大的变革。不同的非线性过程提供了丰富的光场调控方法,为得到目标光场带来极大的便利。非线性光学调控一个重要的应用领域就是提供不同的特殊光源,主要包括:利用和频与倍频过程得到极短的紫外光源[2−4];通过光学参量振荡和差频过程得到红外光源[5−7];通过不同非线性过程的组合得到光学频率梳以及超连续光源[8−10];还有通过自发辐射如自发参量下转换或者自发四波混频过程产生非经典的量子光源[11−14]。非线性光学调控另外一个重要的应用领域是光学精密测量,主要包括:利用倍频过程的光场自相关测量超短脉冲的脉冲宽度[15];通过二阶或者三阶过程实现频率可分辨光学快门(FROG)用于重构超短脉冲的电场[16];利用多光子非线性实现光与物质相互作用中电子的动力学行为的测量[17];另外,非线性频率转换还可用于光场的上转换探测,将红外光场转换到可见波段进行探测,避免红外波段探测器灵敏度低的缺点[18−20]。以上应用都依赖于在不同非线性过程中实现对光场不同自由度的精细调控。

光场具有多个自由度,这些自由度包括偏振、相位、时间、频率、线动量和角动量,通过调控这些自由度可以实现满足不同应用场景的目标光场[21]。在这些自由度中,轨道角动量(OAM)自由度自从1992年被Allen等[22]提出后受到广泛关注并开展了大量研究。由于OAM光束特殊的强度和相位分布以及力学效应,该光束在高速高容量光通信、光镊、成像、精密测量、非线性光学和量子信息中具有非常广泛的应用[23,24]。目前已有的关于OAM光束的研究主要集中于在不同的物理过程中实现OAM光束的产生、调控、传输和探测方面[23,24]。利用非线性过程对光场进行调控无论是对非线性光学还是对结构光场调控都带来了新的机遇。一方面,将结构光场引入非线性光学需要对原有的针对平面波和高斯光束的非线性光学理论进行升级和完善,从而适应结构光场非线性相互作用的需求,进而推动非线性光学物理的发展;另一方面,非线性光学为结构光场的产生、调控和探测提供了非常丰富的技术方法,是对已有线性光学方法的有效补充。

本文综述了近十年来OAM光束在二阶非线性过程中频率转换的研究进展,主要针对准相位匹配晶体。第一部分介绍了OAM光束的基本性质和准相位匹配非线性转换的基本原理。第二部分综述了目前OAM在QPM晶体中频率转换的主要进展,包括:非线性过程中OAM光束的守恒、传输、演化和干涉行为研究;高效率的OAM激光和单光子态频率转换研究;OAM频率转换效率模式非依赖性研究;矢量光束的频率转换研究;以及无后向选择的高维OAM纠缠态的制备研究。最后讨论和展望了OAM在QPM晶体中频率转换的潜在研究趋势和应用方向。

1 轨道角动量光束非线性转换基本原理

1.1 轨道角动量光束简介

角动量是光的一个特殊自由度,光的角动量包括自旋角动量(SAM)和轨道角动量(OAM),总的角动量可表达为J=σ+L,其中σ=±1ħ表示左右旋偏振,L=lħ表示轨道角动量[23,24]。1992年,Allen等[22]证明了具有exp(ilφ)角向相位分布的光束每光子携带lħ的轨道角动量。如图1所示,自旋角动量可以取两个分立的值,而轨道角动量理论上可以取无限个值。

图1 自旋角动量与轨道角动量的简单示意图Fig.1 Simplified images for spin angular momentum and orbital angular momentum

轨道角动量光束的种类很多,如厄米高斯光束、拉盖尔高斯光束、贝塞尔高斯光束和艾里高斯等,这些光束是麦克斯韦方程在傍轴近似下的解析解,并且构成完备正交基,任意其他光束可以写成某种光束的相干叠加态(感兴趣的读者可以参考相关综述文献[23,24])。在这些光束中,对拉盖尔-高斯(LG)光束的研究最为广泛,LG光束的表达式为[22]

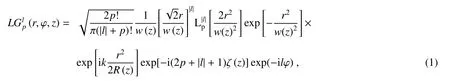
式中:p和l是表征光束的径向和角向特性的两个重要参量,l表示在光束横截面内绕光束一周位相变化2π周期次数,p决定光束的径向节点;w(z)是光束在传播距离为z时位置的束腰;表示拉盖尔多项式;k=2π/λ是波数;R(z)是光束在传播距离为z时的曲率半径;φ是横截面内的极角;ζ(z)是依赖传播距离的Gouy位相。图2给出了几个典型LG模的强度和位相分布。当径向分量p=0时,LG模的强度分布是典型空心光束;而当p≠0时,光束的强度分布是同心圆环,相邻同心圆环的位相相差π。

图2 典型LG模的强度与位相分布。(a),(b)分别为l=2,p=0的强度与位相分布;(c),(d)分别为l=3,p=1的强度与位相分布Fig.2 Typical intensity and phase distribution of LG modes.Images(a),(b)are the intensity and phase distribution of mode l=2,p=0;Images(c),(d)are the intensity and phase distribution of mode l=3,p=1

轨道角动量光束研究的两个重要主题是产生与探测。在轨道角动量产生方面,目前产生方法有很多(如图3所示),主要包括:通过谐振腔的本征模式HG模经过一对柱面透镜进行变换得到[如图3(a)所示][25],全息光栅衍射[如图3(b)所示][26],液晶q波片[如图3(c)所示][27],螺旋相位板[如图3(d)所示][28],液晶空间光调制器[如图3(e)所示][29],微纳环形光栅[如图3(f)所示][30],超表面微纳结构[如图3(g)所示][31],激光器直接产生[如图3(h)所示][32]。在这些方法中,空间光调制器可以非常方便地产生任意大小单个拓扑荷轨道角动量光束和叠加态光束,被广泛用于实验研究。另外,利用微纳器件产生轨道角动量光束也是最近的研究热点和趋势,Fickler等[33]利用微纳器件可以产生拓扑荷超过10000 ħ的轨道角动量光束。南京大学陆延青教授研究组在基于液晶的q波片产生空间光束方面开展了系统的研究,可以产生多种具有特殊性质的空间结构光束[34]。高阶模式激光器也是这些年激光技术研究的热点和发展趋势,如Naidoo等[35]在激光腔中插入q波片,可以直接输出任意庞加莱球上的光束模式。

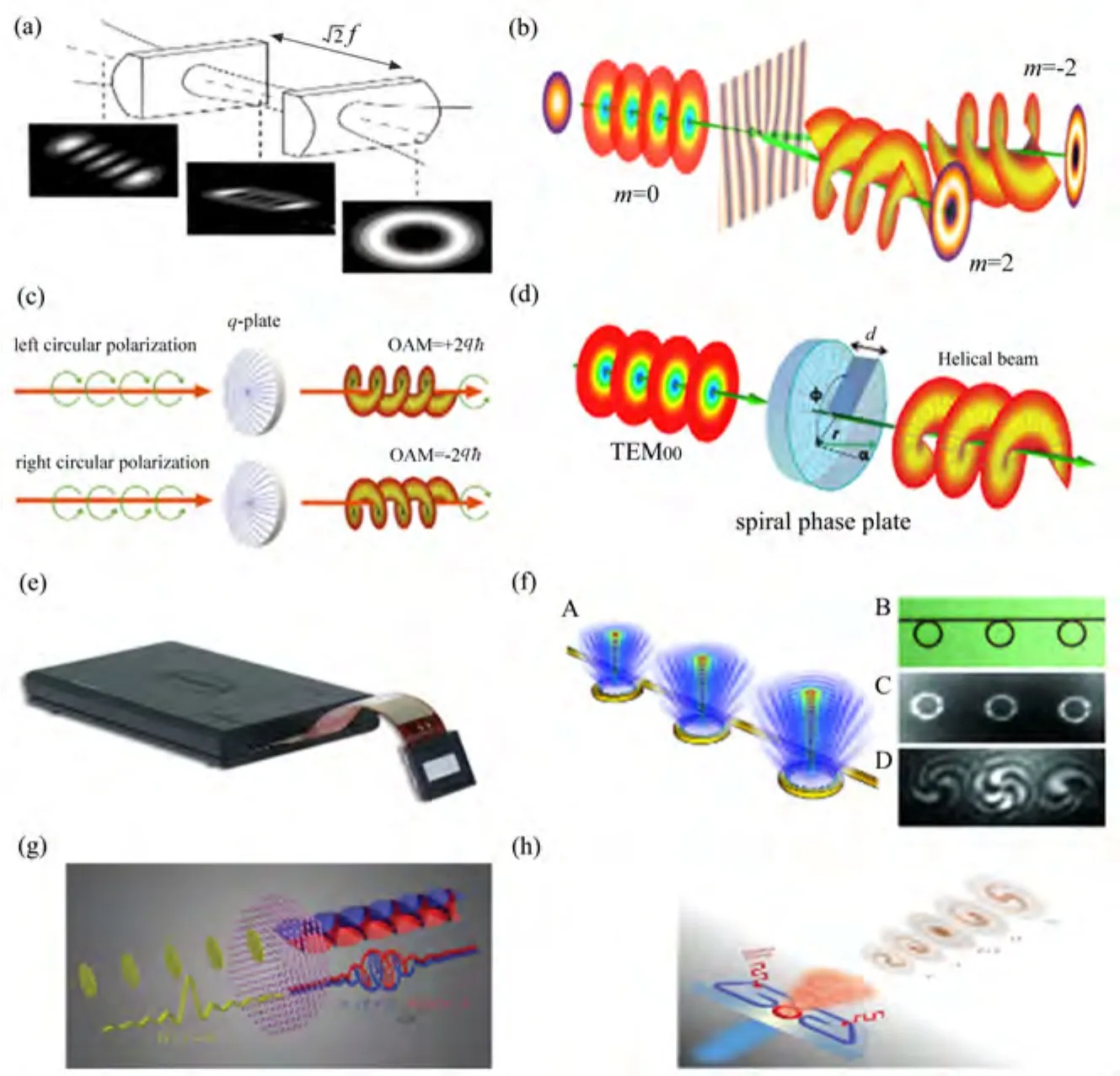
图3 基于不同的方式产生OAM光束。(a)柱透镜变换法[25];(b)全息光栅衍射法;(c)液晶q波片[27];(d)螺旋相位板;(e)空间光调制器;(f)圆环光栅[30];(g)超表面微纳结构[31];(h)半导体激光器直接产生[32]Fig.3 Generation of OAM-carrying light based on different methods.(a)Transformation by using a pair of cylindrical lenses[25];(b)Diffraction by hologram gratings;(c)Liquid crystal q plate[27];(d)Spiral phase plate;(e)Spatial light modulator;(f)Circular micro-ring gratings[30];(g)Dielectric meta-surface[31];(h)Direct generation by using semi-conductor laser[32]

轨道角动量光束的探测是实现相关研究和应用的重要前提,在OAM光束的区分与探测方面研究人员也开展了大量系统的研究。目前主流的用于检测OAM光束的方法包括干涉法[36−42]、几何波前变换法[25,43−45]和投影法[46−48]。干涉法第一个用途是确定单个轨道角动量光束的拓扑荷大小,主要有两种方式[36]:第一种方式是高斯光束与涡旋光束干涉,通过干涉条纹的分叉数目确定拓扑荷大小[如图4(i)];第二种方式是利用特殊设计的MZ干涉仪用于产生具有相反拓扑荷的两个OAM光束的干涉产生花瓣状的干涉条纹,通过条纹的数目确定输入光的拓扑荷大小[如图4(ii)]。对于单个拓扑荷OAM光束的检测,还可以通过柱透镜将LG模式变换成为HG模式从而确定光束的拓扑荷[25]。为了实现具有多个拓扑荷的光束的有效探测,需要对不同拓扑荷进行有效区分,轨道角动量的区分中也有两种方式:级联干涉法[37−42]和几何波前变换法[43−45]。对于干涉法又分为两种:一种是基于双光束干涉方法,通过级联MZ干涉仪可以有效区分不同拓扑荷以及径向分量的轨道角动量光束[如图4(iii)][37−40];另一种是多光束干涉法,通过级联光学谐振腔也可以实现轨道角动量模式的非破坏区分[如图4(iv)][41,42]。

图4 基于干涉方法的OAM光束检测与区分。(i)基于高斯光束与OAM光束干涉的方法检测OAM光束的拓扑荷;(ii)基于相反拓扑荷OAM光束干涉检测OAM光束的拓扑荷;(iii)基于双光束MZ干涉仪级联区分不同OAM光束[39];(iv)基于多光束干涉环形腔级联区分不同的OAM光束[42]Fig.4 OAM-carrying light detecting and sorting based on interferometric methods.(i)Detecting topological charge of OAM-carrying light based on the interference of Gaussian beam with an OAM-carrying light beam;(ii)Detecting topological charge of OAM-carrying light based on the interference of two OAM-carrying beams with opposite topological charges;(iii)Sorting OAM-carrying light based on cascading two beam interference MZ interferometer[39];(iv)Sorting OAM-carrying light based on cascading multi-beam interference ring cavity[42]

几何波前变换方法的原理是将螺旋波前变成依赖于拓扑荷的平面波前,通过傅里叶变换在频谱面上变成分立的点状分布[如图5(i)][43,45];在此基础上研究人员发展了光栅干涉的方法,进一步增强了不同模式的区分度,并有效降低了串扰[44]。投影法是通过将空间结构光束逆变换成高斯光束进行检测,这种方法可以精确地刻画光束状态层析,但是测量过程会破坏光束原有的状态[如图5(ii)][46−48]。

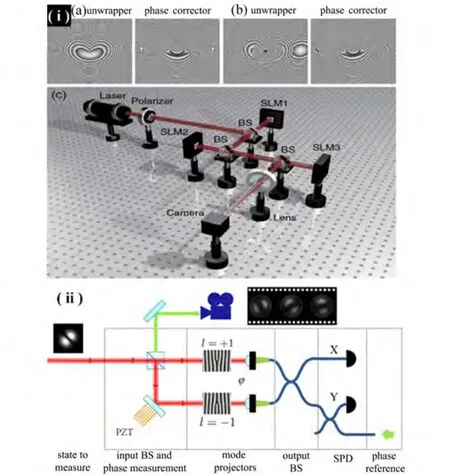
图5 基于几何波前变换法和投影法的OAM光束区分与探测。(i)基于与几何波前变换方法的OAM光束区分[45];(ii)基于模式投影法的OAM量子态测量[46]Fig.5 OAM-carrying light sorting and detecting based on geometric wavefront transformation and projection method.(i)OAM-carrying light sorting based on geometric wavefront transformation[45];(ii)OAM-carrying light detecting based on mode projection[46]

1.2 非线性光学转换基本原理

光场的感生极化场与所加电场的关系可表示为[49]

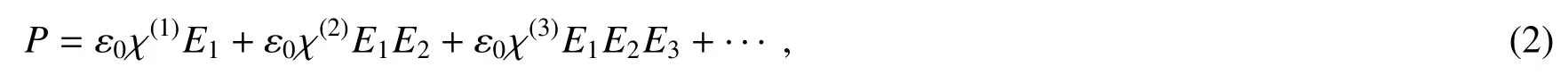
式中:ε0是真空中的介电常数;χ(i)代表第i阶极化张量;ε0χ(1)E1是传统的线性光学研究的对象,与介质的折射率相关;ε0χ(2)E1E2是与倍频、和频、差频、参量放大等现象相关的二阶相应项;ε0χ(3)E1E2E3是与三次谐波产生、布里渊散射有关的三阶相应项。本综述主要讨论与χ(2)相关的二阶非线性效应。主要的二阶非线性过程包括倍频、和频、差频以及参量放大,如图6所示。在这些非线性过程中,第一个重要的条件是相互作用中的能量守恒。当两个频率为ω1和ω2的光束入射到非线性介质时,可以出现多种相互作用过程。以和频过程为例,两个入射光子频率的和是新产生光子的频率,即ω3=ω1+ω2。而对于参量放大来说,一个高频的光子劈裂成频率为ωs的信号光子(Signal)和ωi的闲散光子(Idler),由于能量守恒,ωp=ωs+ωi。如果参量放大过程是在一个光学谐振腔中进行的,就构成了参量放大振荡器(OPO)。

图6 主要二阶非线性频率变换的原理示意图Fig.6 Simplified diagram for main second order nonlinear frequency processes

二阶非线性的主要描述方式是耦合波方程,在连续光场相互作用下的方程为[49]

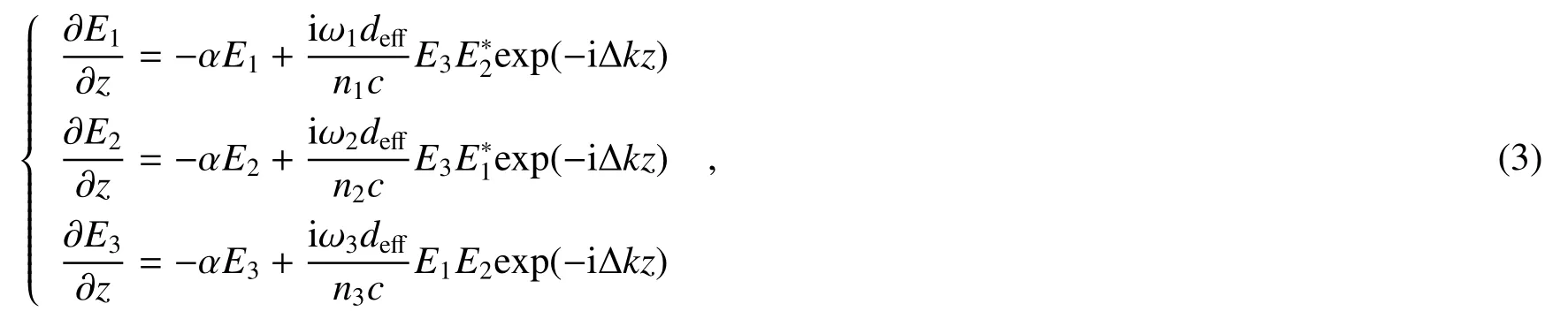
式中∆k=k3−k1−k2是三波混频过程中的位相失配,deff是取决于二阶极化张量的有效非线性系数,其具体表达式取决于入射光场的偏振和位相匹配条件。

相位匹配是实现高效率非线性转换的关键,目前的相位匹配方式主要包括双折射相位匹配(BPM)和准相位匹配(QPM)。双折射相位匹配是利用晶体的双折射效应,使得在某一个入射角下参与相互作用的光束的相速度相同;准相位匹配是利用晶体中自发极化电筹的周期性翻转得到一个有效的倒格矢,利用倒格矢补偿不同光场的相位失配。QPM相对于BPM具有以下优点:光束沿光轴传播,无走离效应;可以利用到最大的有效非线性系数;在晶体的整个透明窗口内都可以实现相位匹配。以倍频为例,可以通过周期性改变晶体固有电筹的方向引入了一个有效的光栅矢量kQ,图7(a)简单演示了如何用倒格矢来补偿倍频过程中的位相失配。

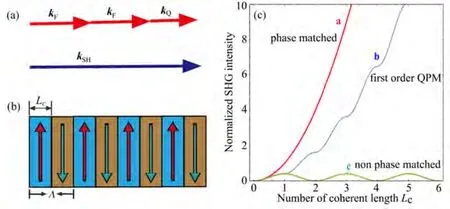
图7 准相位匹配基本特点。(a)利用光栅矢量kQ补偿基频光的波矢kF与倍频光的波矢kSH之间的失配;(b)准相位匹配晶体内极化电筹反转情况;(c)不同相位匹配情况下的倍频功率与晶体长度之间的关系Fig.7 Properties for quasi-phase matching.(a)The effective grating wavevector kQcan be used for compensating the mismatch between kFand kSH;(b)A picture of domain inverse in quasi-phase matching crystals;(c)Intensity of second harmonics beam with crystal length at different phase matching condition

1962年,Armstrong等[50]首次提出准相位匹配技术。在数学上,极化方向的改变等效于π位相改变。从工程角度上看,在倍频过程中,选择合适的晶体电筹极化反转长度,其产生的π位相偏移正好补偿基频光与所产生倍频光的位相差。总的位相失配在一个周期内保持为零,保证有效的非线性转化。尽管在准相位匹配中有效非线性系数减小了2/π倍,但是由于可以使用最大的极化张量元d33,所以相比于双折射位相匹配晶体仍然有很大的提高。最高的有效非线性转换可以用一阶准相位匹配来实现,在一阶准相位匹配中,极化反转周期是一个相干长度Lc[如图7(b)]。如果极化反转的周期是三个相干长度,就称为三阶准相位匹配。图7(c)展示了不同位相匹配条件下倍频功率与晶体长度的关系。准相位匹配周期Λ=2Lc可以设计在任何想要的温度下。

在准相位匹配晶体中,相互作用光之间的相速度失配可以用一个周期性调制的非线性系数d来描述,将周期性的非线性系数傅里叶展开成[51]

式中:dil是介质的非线性系数;Gm是m次谐波的傅里叶系数;m阶光栅矢量定义为kmQ=2mπ/Λ,这里Λ是空间调制周期;其中第m阶空间谐波所对应的有效非线性系数为deff=dilGm。当非线性系数的符号被周期性调制,那么第m次傅里叶系数可以表示为Gm=2sin(mπD)/(mπ),其中D是占空比,取决于反转的电筹长度与调制周期Λ的比例。在最佳占空比下正弦函数取值为1,因此deff=2dil/(mπ),从该式可以看出高阶准相位匹配的效率要比一阶准相位匹配的效率低。

2 OAM频率转换主要进展

2.1 非线性过程中OAM光束的守恒、传输和演化行为研究

早在1996年,Allen及其合作者研究了不带径向模式的OAM模式与带径向参数的OAM光束在BPM晶体中的倍频过程,证明了OAM光束在倍频过程中的守恒特性,此后该方面的研究进展一直比较缓慢[52]。2013年,南京大学陆延青教授研究组第一次通过数值模拟的方式证明了OAM光束在准相位匹配PPLN晶体中的守恒特性[如图8(i)][53]。自此开始,基于准相位匹配的OAM光束频率转换得到广泛研究并且取得重要进展。其中的主要进展包括:2014年,本研究组在0型PPKTP晶体中实现了单个轨道角动量和叠加态从795 nm到397.5 nm的倍频研究,证明了在倍频过程中轨道角动量的守恒特性,并且研究了叠加态光束的干涉行为[如图8(ii)][54];2015年,本研究组进一步实现了两个轨道角动量光束的和频相互作用,研究了795 nm的高斯光束及拓扑荷为±2的OAM光束与携带OAM拓扑荷为1∼8的1550 nm光束的和频,在短晶体或者强聚焦下得到了和频过程OAM光束演化的解析公式,为研究非线性转换中光束的传输演化奠定了基础[如图8(iii)][55];在得到解析结果后,本研究组又系统研究了和频过程中光束的传输演化行为,包括正负拓扑荷光束和频光场演化、单个OAM光束与叠加态和频的演化和两个OAM光束叠加态的演化[如图8(iv)][56];2021年,本研究组通过级联倍频过程实现了1560 nm的OAM光束到390 nm OAM光束的四次谐波产生[57]。南京大学祝世宁院士、陆延青教授和肖敏教授等研究组也系统开展了OAM光束的倍频、和频及三倍频等方面的研究,他们基于自己加工的准相位匹配晶体开展了相关工作[58−60]。此外,华东师范大学曾和平教授研究组也在轨道角动量光束的频率转换方面开展了系列工作[61]。

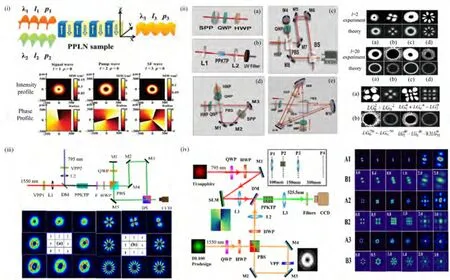
图8 准相位匹配二阶非线性过程中的OAM光束转换。(i)PPLN晶体中OAM光束和频数值模拟研究[53];(ii)PPKTP晶体中OAM光束及叠加态光束的倍频研究[54];(iii)PPKTP晶体中OAM光束的和频转换研究[55];(iv)PPKTP晶体中OAM和频转换过程中的传输与演化研究[56]Fig.8 Second order nonlinear frequency conversion based on quasi-phase matching crystals for OAM-carrying light beams.(i)Simulations of sum frequency generation of OAM-carrying light beams in PPLN crystal[53];(ii)Second harmonics generation of single and superposition of OAM-carrying beam in PPKTP crystal[54];(iii)Sum frequency generation of OAM-carrying beam in PPKTP crystal[55];(iv)Evolution and propagation of sum frequency generated OAM-carrying beams in PPKTP crystal[56]

为了研究OAM光束在二阶非线性过程中的守恒、传输和演化特性,根据耦合波方程(2),在假设传输损耗为0并且晶体较短或者紧聚焦的情况下,可以推导出和频过程中产生的光场随着距离的光场演化。假设参与和频的OAM光束的模式为,其中m和n为两束光的拓扑荷,在晶体中心束腰位置的和频光场为[55]

式中w1和w2为两个光束的束腰大小。和频光场经过传输演化变为

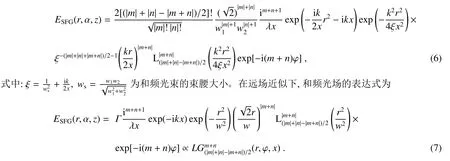
(6)式可以用于模拟产生的OAM光束的传输和演化行为,如文献[54]中产生的倍频光场的传输演化和文献[56]中和频光场的传输和演化。(7)式清晰地表明在和频光程中轨道角动量是守恒的,lSFG=l1+l2。

矢量涡旋光束具有非均匀的偏振分布,因此直接转换后无法得到标准的矢量光束。实现矢量光束的转换主要有两种方式:第一种是采用Sagnac干涉仪或者MZ干涉仪结构将两个偏振模式分开转换,再将转换后的两个偏振再合束[62−66];第二种方式是通过正交叠加的晶体分别对两个偏振模式进行转换[67−69]。2019年,本研究组利用Sagnac干涉仪结构在0型PPKTP晶体中实现了1560 nm矢量光束到780 nm矢量光束的倍频,并且研究了倍频光束的拓扑荷和偏振特性[如图9(i)][62];同年,上海交通大学陈险峰教授研究组利用正交叠加的角度相位匹配晶体实现了完美矢量涡旋的倍频研究[如图9(ii)][69],并且后续利用同样的结构通过倍频实现了紫外矢量涡旋的产生[68],此外该研究组还利用MZ干涉仪结构实现了矢量涡旋的倍频[63];最近,南京大学汪喜林教授和哈尔滨理工大学朱智涵教授研究组也利用Sagnac干涉仪结构在II型准相位匹配晶体中实现了矢量涡旋的频率转换[64−66]。

图9 基于不同结构的矢量光束倍频转换。(i)基于准相位匹配晶体及Sagnac干涉仪结构的矢量光束倍频转换[62];(ii)基于两块正交叠加的角度相位匹配晶体的完美矢量光束倍频研究[69]Fig.9 Frequency conversion of vector vortex beam based on different configurations.(i)Second harmonics generation of vector vortex beam based on quasi-phase matching crystal in a Sagnac loop interferometer[62];(ii)Second harmonics generation of vector vortex beam based on birefringent phase matching for two crystals with orthogonal optical axes[69]

下面以Sagnac干涉仪结构的矢量涡旋光束倍频为例,阐述矢量光束倍频的基本原理。输入的基频矢量光束的表达式为[62]

该光束通过Sagnac干涉仪进行直接倍频结果为

从(9)式可以看出,标准的矢量光束直接倍频产生的光束不是标准的矢量光束,其中含有不含角动量的高斯光束成分,该光束的偏振分布不满足柱对称条件。为了得到标准的倍频矢量光束,需要将基频矢量光束通过四分之一波片先变成指数形式的光束,该光束的表达式为

该光束在倍频后保持原有的形式,再将该形式的倍频光束通过四分之一波片倍频产生标准的倍频矢量光束

2.2 高效率的OAM频率转换研究

提高非线性转换效率是非线性光学研究的重要主题,为了让OAM光束的频率转换具有应用价值,高效率的转换至关重要。目前提升OAM非线性转换效率的手段主要有两种:一种是基于超快高峰值功率的脉冲光为泵浦光[如图10(i)][61];另外一种方式是针对连续光泵浦,可以通过腔增强的方式增强泵浦功率,从而可以大幅度地提高转换效率[如图10(ii)][70−73]。对于脉冲泵浦的情况,华东师范大学曾和平教授研究组通过ps脉冲的和频过程,对于OAM拓扑荷为1的光束将转换的量子效率提升到68%[61];本研究组通过腔共振技术,在2015年实现了OAM拓扑荷为2的光束的倍频,将倍频效率提升到10.3%[70];在此基础上,本研究组将其拓展到量子光学领域,通过单共振的谐振腔分别实现了1550 nm标记轨道角动量单光子态和轨道角动量纠缠态到525 nm的量子频率转换,证明了转换过程中的单光子特性、相干特性和纠缠特性可以有效地保持[如图10(iii),(iv)][71,72]。此外,本研究组还实现了OAM量子比特的差频转换[73]。为了系统地研究OAM光束参与非线性过程的转换效率与实验参数之间的关系,本研究组将高斯光束的转化效率公式拓展到了一般的情况,在泵浦光转换损耗很低的情况下得到了转换效率公式的解析结果[71]。

图10 高效率的OAM光束频率转换方式与进展。(i)基于脉冲泵浦的高效率OAM光束频率转换;(ii)基于单共振光学谐振腔结构的高效率OAM光束频率转换;单共振谐振腔用于高效率的(iii)OAM标记单光子频率上转换[71];(iv)OAM纠缠的频率上转换[72]Fig.10 Methods for high efficiency frequency conversion and some recent progress.(i)High efficiency OAM-carrying beam conversion based on intensively pulsed pump configuration;(ii)High efficiency OAM-carrying beam conversion based on cavity-enhanced configuration,and single resonance cavity for efficiently frequency conversion of(iii)heralded OAM state[71];(iv)OAM entangled state[72]

为了实现高效率的OAM单光子态频率转换[71],可以使用单共振的光学谐振腔。在实验中,谐振腔与795 nm的基频光共振,携带OAM的单光子态从谐振腔中单次通过。谐振腔共振时,其腔内循环功率可以达到约20 W,对于拓扑荷l=0,1,2的OAM单光子态的转换效率分别为22.4%、8.33%和2.96%。为了表征转换后光子的相干性是保持的,利用一个Sagnac干涉仪产生偏振与OAM的混杂叠加态,通过和频转换后其单光子态为,通过二分之一波片改变相对相位θ可以得到该量子态的干涉曲线,实验测得的干涉可见度为88.5%±5.6%。基于同样的方式,本研究组实现了OAM纠缠频率转换器[72],在实验中通过偏振纠缠源进行模式转换变成轨道角动量纠缠,分别实现了OAM量子比特、OAM与偏振混杂纠缠以及OAM纠缠的转换,实验中对于OAM量子比特转换的平均保真度为0.954±0.016;对于OAM与偏振混杂纠缠其重构的密度矩阵保真度为0.837±0.025;对于OAM纠缠,其在两组基矢下的干涉可见度分别为0.955±0.023和0.750±0.062,贝尔不等式S值大小为2.39±0.12。

不同OAM光与高斯光束相互作用的量子效率与实验参数的关系对于OAM光子频率转换至关重要。在泵浦弱耗散情况下,本研究组推导了不同OAM模式参与非线性的转换效率公式。对于单光子频率转换,其中P为腔内循环功率,Pmax是最佳转换时的功率大小。对于OAM光束与高斯光束和频,其和频功率与实验参数的关系可表示为[71]

式中:P为泵浦功率,Ps为信号光子功率,deff为有效非线性系数,ε0为真空介电常数,c为真空中的光速,ns、nSFG为信号与和频光子的折射率,λs、λSFG为信号与和频光子的波长,h(l,ξ)为聚焦参数,l为拓扑荷大小。

2.3 OAM频率转换效率模式非依赖性研究

在轨道角动量光束频率转换过程中,泵浦光束与携带不同拓扑荷的OAM光束的交叠程度不一致,因此不同轨道角动量光束在频率变换过程中会出现效率不一致的情况,这种情况会导致轨道角动量高维叠加态在频率变换后发生畸变,保真度会下降[71]。为此,本研究组尝试了两种方式,第一种方式是通过光学成像的方式将OAM光束产生位置的光场成像到待转换晶体的中心,这样不同轨道角动量光束虽然具有不同的空间相位分布,但是其强度分布是一致的。基于这项原理,本研究组利用fs光泵浦验证了拓扑荷为0∼3的条件下从1550 nm倍频到775 nm条件下转换效率随泵浦光功率的变化一致,最高转换效率可达到14%[如图11(i)][74]。另外一种方式是改变泵浦光的光场分布,将高斯泵浦光换成平顶光束作为泵浦,由于平顶光束与不同拓扑荷的轨道角动量光束的交叠程度一样,原则上可以消除不同模式转换时效率的不一致。基于此原理,本研究组实现了标记OAM单光子高维态的频率转换,并且证实了平顶光束转换相对于高斯光束转换保真度有明显的提升[如图11(ii)][75]。

图11 频率转换效率不依赖于OAM模式实验进展。(i)基于成像的方式实现倍频效率不依赖于fs OAM光束的拓扑荷[74];(ii)基于平顶光束实现高保真度的高维轨道OAM单光子态的频率转换[75]Fig.11 The experimental progress for realizing conversion efficiency independent of input signal modes.(i)Realizing of conversion efficiencies independent of input fs OAM modes in second harmonics generation[74];(ii)High fidelity frequency conversion of high dimensional OAM superposition state based on flat-top pump beam[75]

2.4 泵浦调制制备无后向选择OAM高维纠缠态

基于OAM自由度的高维量子态制备一直是量子信息领域的研究热点,传统方案中通常通过使用短晶体、大泵浦光斑和相位匹配调控来实现产生光子维度的调控,为了得到最大纠缠态往往需要通过后向选择来获得,后向选择可以得到高维OAM最大量子纠缠态,然而会牺牲产生光子的亮度[76−79]。由于自发参量下转换过程满足轨道角动量守恒特性,通过改变泵浦光的模式成分可以有效地影响下转换过程中产生的状态。基于这种原理,2018年,本研究组与俄罗斯Kulik研究组各自独立实现了通过叠加态的光束泵浦周期性极化PPKTP晶体制备三维最大纠缠态,并且制备的三维纠缠态的相对相位可以任意调控[80,81];在此基础上,本研究组进一步利用具有指数形式的光束泵浦实现了高维纠缠态的制备,从理论上证明可以产生高于10维的纠缠态制备,在实验中对5维纠缠做了系统的表征[82]。泵浦光调制方法提供了另外一种产生高维OAM纠缠态的有效方法,该方法的优点是在长晶体中可以进行强聚焦,在光子产生效率上有大幅度的提升。

自发参量下转换过程中满足角动量守恒,泵浦光子与产生的信号和闲频光子的角动量满足lp=ls+li。对于单个态泵浦,产生的光子对量子态为;与之对应,当用(其中CL=|CL|eiθL)叠加态的泵浦激光泵浦时,产生的光子对状态。选取合适的叠加系数,用C−2|−2〉p+C0|0〉p+C2|2〉p态进行泵浦时,可以产生基于此原理,当用 |L〉p=|0〉p+|2〉p+|−2〉p的泵浦光进行泵浦时,可以产生无后向选择的最大纠缠态|φ〉MES=|−1〉s|−1〉i+|0〉s|0〉i+|1〉s|1〉i。与此同时,当改变泵浦光叠加态的相对相位时,产生的三维最大纠缠态的相对相位也随之改变。当用 |−2〉p+eiθ0|0〉p+eiθ2|2〉p态进行泵浦时,产生的纠缠态随之变为|φ〉MES=|−1〉s|−1〉i+eiθ0|0〉s|0〉i+eiθ2|1〉s|1〉i。在实验中 (如图 12)[80],本研究组研究了改变泵浦光系数所产生的OAM双光子的空间频谱变化情况,发现在合适的系数下可以得到最大的三维纠缠态。另外,还研究了泵浦光叠加态相对相位的相干传递现象。最后通过高维干涉、高维贝尔不等式和量子态层析表征制备的纠缠态的特性。实验测量贝尔不等式S值为S3=2.3735±0.0159,重构的密度矩阵的保真度为F=0.8581±0.0028。

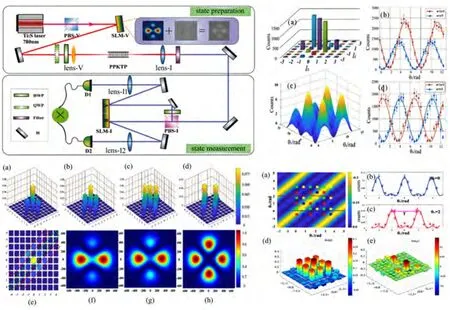
图12 基于泵浦调制的无后向选择任意可编辑三维最大纠缠态的制备[80]Fig.12 Preparation of arbitrary engineered three dimensional maximum entangled state without post-selection based on pump mode modulation[80]

3 讨论与展望

系统综述了轨道角动量光束在准相位匹配晶体中参与非线性相互作用的基本物理体系和主要进展情况。从已有的研究看,目前在基于一维准相位匹配的OAM频率转换中,其基本物理体系已经构建,主要的技术难点也基本被克服。未来关于OAM频率转换研究的主要趋势体现在以下几个方面:1)其他类型特殊光束的应用,比如时空涡旋光场、空间阵列光场和自旋轨道耦合的空间光场[83−87];2)特殊微结构材料的应用,比如二维、三维准相位匹配晶体,基于超表面的非线性表面材料等[88−94];3)研究的波长范围的拓展,可以从已有的近红外波段拓展到中远红外、太赫兹波段,以及往短波极紫外波段拓展[95−99]。新型光场调控给相关应用提供了重要的工具,为光学技术的发展不断贡献力量,该领域的研究依然具有很旺盛的生命力。