基于UML 活动图的无人车变道可靠性预测
吴兆贤,吴培培
(浙江理工大学 信息学院,浙江 杭州 310018)
0 引言
随着智能化的不断发展,无人车成为国内外研究热点。无人车不仅具备加速、减进、后退以及转弯等常规的汽车功能,还可以实现行人车辆避让、自动变道、自动转向、红绿灯识别等功能。其中,变道行为是两大基本驾驶行为之一,对车辆行驶安全和交通稳定具有重要意义[1]。据资料显示,车辆变道过程是交通事故的高发时段,对车辆变道行为进行研究有着重要的现实意义。谷歌RX450h无人车曾与一辆公共汽车发生刮擦,当时这辆无人车发生交通意外就是在它的变道过程中。无人车变道的可靠性问题是一个亟需解决的难题。
可靠性是指在特定的时间区间完成规定功能的能力[2];可靠性是软件的非功能质量属性,能够定量地对软件的失效行为进行评估[3]。基于体系结构的分析方法主要可以分为两类:基于路径的方法和基于状态的方法[4-5]。基于路径的方法常常运用在软件所有执行路径可靠性为已知的条件下;基于状态的方法根据软件中的构件及其交互关系,得出系统可靠性。早期的可靠性分析利用软件测试或运行时期统计的数据对软件可靠性进行度量和分析,这样度量出的结果较为精确。但是在该阶段才发现度量出的可靠性不满足要求,再对软件作出改进将花费大量的人力和物力。因此,在软件早期设计阶段对可靠性进行预测,从而指导软件开发很有必要。
由于车辆变道是驾驶中高频且十分重要的一项驾驶行为,本文针对无人驾驶车辆的变道行为进行可靠性预测。无人车可靠性预测结果可以在无人车设计阶段反映车辆变道效果,从而为设计人员提供是否需要改良的参考。
1 相关工作
统一建模语言(Unified Modeling Language,UML)通常被用作建立系统模型[6-8]。将非功能属性添加到简单的UML 模型中,从而为可靠性分析提供条件。对于构件化软件体系的可靠性分析而言,马尔可夫链和马尔可夫过程是非常有效的分析模型。文献[9]中通过构件转移图将UML模型转化为马尔可夫链;文献[10]中将MARTE(Modeling and Analysis of Real Time and Embedded Systems)模型通过定义的映射规则转化为马尔可夫决策过程。
软件系统组件间的错误传播是反映软件产品可靠性的量化因素。Malik[11]等提出一个针对基于组件的软件进行可靠性评估的框架,该框架考虑了系统组件之间的错误传播概率。并且,将方法应用于3 种场景的系统中,证实了该方法的有效性。但是该方法在评估可靠性时需耗费大量的时间和精力。文献[12]提出一种分析软件中数据错误传播的方法,引入了错误渗透率的概念,即输入信号中的一个错误渗透到一个输出信号中的概率。此外,还提出了一套参数用以度量错误渗透率,这些参数所描述的是模块间数据流的错误传播行为。文献[13]提出在计算软件可靠性时根据构件失效传播概率矩阵引入构件失效传播行为,但在实验时只是假设构件失效传播矩阵为已知,而并未实际计算。
目前,关于无人车的可靠性研究较少。文献[14]提出一种基于无人驾驶系统的可靠性建模分析方法,该方法采用架构分析与设计语言和错误模型附件建模技术,但是只停留在理论层面,并未通过实验对无人驾驶系统可靠性进行预测分析。
本文结合文献[9]和文献[12],对基于长短期记忆网络LSTM(Long Short-Term Memory,LSTM)的无人车变道行为可靠性进行预测。首先通过UML 对无人车的变道过程进行建模,对于感知模块和LSTM 模块之间的故障传播概率利用错误渗透率进行计算。将UML 模型利用映射规则转换成DTMC 模型,再基于构件转移图将UML 模型转换成DTMC 模型。分别根据这两个DTMC 模型运用PRISM[15]工具进行可靠性预测,并进行结果比较。
相比于文献[13]中计算可靠性时利用假定的失效传播矩阵,本文通过实验对LSTM 模块的错误渗透率进行计算,更具有现实意义。相比于文献[14]对无人驾驶系统的可靠性研究只停留在理论阶段,本文通过具体的建模和实验对无人车变道行为的可靠性进行了预测。
2 UML 建模
2.1 无人车软件架构
无人车的核心在于“智能”。典型的无人车软件架构总体分为感知、决策和控制三大部分。决策系统可以划分为行为决策模块和轨迹规划模块,控制系统可以划分为轨迹跟踪模块和底层控制模块。
LSTM 网络在处理时序问题时有很强的信息获取能力和表征能力。车辆的轨迹序列也是一种时间序列,LSTM可以在预测车辆变道时将车辆的历史轨迹考虑进去,从而达到更好的变道预测效果。目前,越来越多的研究人员将LSTM 神经网络应用于无人车的自主变道领域[16-18]。由于LSTM 网络在无人车变道领域的预测效果显著,本文将基于LSTM 网络的变道行为进行建模和可靠性预测。本文基于LSTM 的无人车智能变道系统架构如图1所示。

Fig.1 System architecture for realizing lane change of unmanned vehicles图1 无人车变道系统架构
2.2 无人车变道行为的UML 活动图
图2 为无人车变道过程的UML 活动图,活动图中添加了泳道信息,用以表示活动的执行对象。
如图2 所示,在无人车变道过程中涉及到的模块有感知模块、行为决策模块、轨迹规划模块、轨迹跟踪模块、底层控制模块。模块的名称标注在泳道上方,该模块负责泳道内的全部活动。无人车先通过感知模块的传感器收集自身车辆信息和周围相邻车道车辆信息;信息经过融合处理后被输入到LSTM 模块中;LSTM 模块利用输入的数据进行车辆变道意图预测,将变道意图的预测结果作为指令传给轨迹规划模块。LSTM 模块判断无人车是否发生变道时,可能会发生变道和继续跟随的情况,发生的概率分别为0.31 和0.69,该值来源于传统经验。轨迹规划模块接收指令后,经过计算后得到车辆的运动目标点和目标速度,然后将要求传递给轨迹跟踪模块;轨迹跟踪模块通过分析、计算后得到关于转向角、油门和制动的具体指令,再将指令传给底层控制模块;底层模块的转向控制系统、油门控制系统、制动控制系统再对无人车的车身进行控制。LSTM 模块作出的决策可能是变道,也可能是继续跟随。这两种条件下的后继轨迹规划、轨迹跟踪和底层控制在难度和复杂程度上都有着显著区别,当LSTM 模块作出的决策是不变道即继续跟随时,其后续活动明显更加简单。因此,在活动图中对不同情况下的后继轨迹规划、轨迹跟踪和底层控制用不同的活动节点加以区分。

Fig.2 Unmanned vehicle lane change activity图2 无人车变道活动
3 基于错误渗透率的故障传播
在进行可靠性评估时,通常会默认组件或模块的故障必定会引起系统失效。实际上,当系统中的某个模块将错误输入到下游模块时,下游模块可能会不受该错误的影响,即下游模块内部可能将来自上游模块输入的故障“遮盖”,仍然产生正确的输出。LSTM 神经网络的鲁棒性决定了感知模块输出的故障并不一定会渗透到LSTM 模块的输出。错误渗透率指模块输入的错误渗透到输出的概率,可用于分析故障传播行为。
由文献[12]对于错误渗透率的定义可知输入输出对之间的错误渗透率以及模块的错误渗透率。如图3 所示,模块M有m个输入和n个输出。式(1)为模块M的输入i和输出k之间的错误渗透率。为模块M的输入i发生错误时,模块M的输出k发生错误的概率。此度量显示软件模块的输入/输出对在输入上发生的错误“渗透性”程度。以单个输入输出之间的错误渗透率为基础,式(2)为模块M的错误渗透率,用以度量模块M输入上的错误渗透到输出的概率。
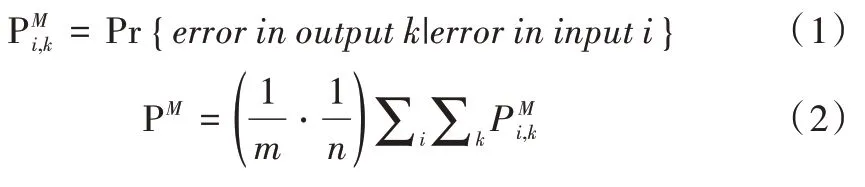

Fig.3 Software module with m inputs and n outputs图3 具有m 个输入和n 个输出的软件模块
如图4 所示,模块A 的输入出现故障的概率为Pf,模块A 的错误渗透率为PA,则模块A 输入出现故障且故障渗透到输出的概率为PfPA,输入出现故障且故障被遮盖的概率为Pf(1-PA)。通常在进行可靠性评估时,会假定模块输入的故障必定会渗透到模块输出,即默认模块的错误渗透率为1。

Fig.4 Fault propagation based on error permeability图4 基于错误渗透率的故障传播
图5 反映了考虑LSTM 模块鲁棒性的情况下感知模块和LSTM 模块之间的故障传播情况,如式(3)所示感知模块输出的每维信息不将故障传递给LSTM 输出的概率为R(C0)+ (1-R(C0))(1-PC1),其 中PC1为LSTM 神 经 网 络 的错误渗透率,(1-R(C0))(1-PC1)表示由于LSTM 的鲁棒性,感知模块输出的信息出现故障但没有渗透到LSTM 输出的概率。

式(4)表示在考虑LSTM 鲁棒性情况下感知模块收集的n维信息均未将故障传递给LSTM 模块输出的概率。


Fig.5 Fault propagation considering robustness图5 考虑鲁棒性的故障传播
4 UML模型映射为DTMC模型
UML 模型不能直接作为可靠性预测工具的输入,而DTMC 模型是有效的可靠性分析模型,可以保障可靠性分析的精确性。本文将基于映射规则将UML 模型转换为DTMC 模型。
DTMC 可定义为一个五元组D=(S,P,s0,AP,L),其中S表示全部状态的有限集合;P:S×S→[0,1]是迁移概率函数,∀s∈S,∑s′∈SP(s,s′)= 1;s0∈S是初始状态;AP 是原子命题集合;L:S→2AP是可以将每个状态映射到原子命题集合AP 里的标号函数[19]。
本文活动图包含图2 中所示的元素。活动图到DTMC模型转换的思路是将初始节点(Init Node)、分叉节点(Fork Node)和汇合节点(Join Node)的后继工作流分别转换为模型Init_DTMC、Fork_DTMC 和Join_DTMC。通过全局变量实现模型之间的通信。具体的映射规则可参考文献[10]中将MARTE 模型将转换成马尔可夫决策过程[20]的方法。
系统中各模块的可靠性如式(5)所示。

其中,k2、k3、k4分别为轨迹规划模块(C2)、轨迹跟踪模块(C3)、底层控制模块(C4)在变道条件下的难度系数。
感知模块(C0)、行为决策模块(C1)的可靠性分别用P0、P1表示。可靠性指系统在特定条件下完成规定功能的能力,不同条件下模块成功完成规定功能的可能性不一样,即不同条件下模块的可靠性也会不同。变道条件下的后继轨迹规划、轨迹跟踪和底层控制就难度和复杂程度而言,显然高于继续跟随条件下的相应活动。引入难度系数区分不同条件下C2、C3、C4模块的可靠性,难度系数越高,模块的可靠性就越低。模块C2、C3、C4在继续跟随条件下的可靠性值分别为P2、P3、P4,在变道条件下的可靠性值分别为P2(1-k2)、P3(1-k3)、P4(1-k4)。
自主变道的每一步活动都是由无人车系统中的模块执行,图2 中通过泳道显示了活动节点(S0,S1,...,S22)和模块(C0,C1,...,C4)的对应关系。活动节点的可靠性由负责该活动模块的可靠性决定。这里活动节点可靠性指该活动节点不会导致后继活动节点失效的概率。表1 显示了活动图中各活动节点的可靠性。

Table 1 Active node reliability表1 活动节点可靠性
活动节点S0表示感知模块对自身车辆信息进行收集,自身车辆信息中包含4 维信息,即S0可继续划分为4 个原子活动节点,由式(4)可知S0的可靠性为[P0+ (1-P0)(1-PC)]4。同理,由式(4)可知S1的可靠性为[P0+ (1-P0)(1-PC)]8。活动节点S3~S5、S6~S9和S10~S12分别为模块C2、C3、C4在继续跟随条件下的活动,其可靠性即为对应模块在继续跟随条件下的可靠性。活动节点S13~S15、S16~S19和S20~S22分别为模块C2、C3、C4在变道条件下的活动,其可靠性即为对应模块在变道条件下的可靠性。
图2中UML 活动图转换得到的DTMC 模型如图6所示。
其中,end1状态表示LSTM 模块在针对是否变道作出的决策为不变道的情况下,无人车以车身继续跟随作为结束;end2表示当LSTM 模块作出的决策为变道的情况下,无人车以车身执行变道作为结束。在DTMC 模型中添加了fault 状态,fault 状态表示系统在执行中出现了故障。DTMC中某个状态到fault 状态的概率由对应活动节点的可靠性决定,当对应活动节点的概率为p 时,该状态到fault 的概率为1-p。
5 实验与分析
5.1 LSTM 模块的错误渗透率
本文将LSTM 神经网络[17]作为无人车变道中的行为决策模块。如图7 所示,感知模块将收集到的自身车辆信息和周围车辆信息输出到LSTM 模块,由LSTM 模块给出变道决策。关于自身车辆的信息有4 个输入,其中Acc 为车辆加速度,Turning _angle 为车辆相对于道路的转向角度,Global_x、Global_y 分别为车辆相对于车道的全局横向和纵向两个车辆位置。关于周围信息有8 个输入,其中Left_lane_exist、Right_lane_exist 分别表示左车道和右车道是否存在,当值为1 时表示车道存在,当值为0 表示车道不存在。Front_dis、Rear_dis 分别表示自身车辆与前方车和后方车的纵向距离,Left_front_dis、Left_rear_dis 分别表示自身车辆与左前方和左后方车辆的纵向距离,Right_front_dis、Right_rear_dis 分别表示自身车辆与右前方和右后方车辆的纵向距离。

Fig.6 DTMC model converted from activity diagram图6 活动图转换的DTMC 模型

Fig.7 Interaction between perception module and LSTM module图7 感知模块和LSTM 模块交互
由式(2)知,要计算LSTM 模块的错误渗透率,需要分别知道12 个输入中每个输入发生错误时引起的LSTM 模块输出偏差的概率。本文LSTM 模块错误渗透率的实验基于故障注入(Fault Injection,FI),故障注入是一种人为地将故障或错误引入系统的可靠性验证技术。现选取6 000 组数据,分别针对12 维输入数据中的每一维数据注入故障,将注入故障后的预测结果与本来的预测结果进行对比,即可得12 维输入中每维输入发生错误时引起的LSTM 模块输出偏差的概率。本文中,对于Left_lane_exist、Right_lane_exist采取的故障注入方式是将原值取反。除此之外的10 维输入是在原值的基础上通过修改代码随机扩大或减小2 到5倍来注入故障。实验结果如表2 所示,Nerror为输入错误时输出发生错误的次数,Perror为每个输入与LSTM 模块输出之间的错误渗透率。由式(2)和实验结果可计算得出LSTM模块的错误渗透率为
5.2 利用映射所得DTMC 进行可靠性预测
本文无人车变道可靠性研究从无人车收集自身及周围环境信息开始到无人车继续跟随或无人车车身开始执行变道行为过程中无故障发生的概率,即本文中无人车变道可靠性的值为从开始最终能到达end1或end2状态的概率。
将由DTMC 模型得到的PRISM 代码及式(6)输入到模型检测工具PRISM 中。

Table 2 LSTM neural network input and output error penetration rate表2 LSTM 神经网络输入输出错误渗透率

对于图2 的无人车变道过程,基于当前软件架构,在P0= 98.2%,P1= 94.9%,P2= 98.1%,P3= 98.9%,P4=99.2%,K2= 0.012,K3= 0.010,K4= 0.001 时,由PRISM 模型检测工具得到可靠性值,如图8 所示,无人车变道可靠性值约为76.47%。
5.3 利用构件转移图的可靠性预测
上文可靠性预测是基于UML 活动图根据映射所得的DTMC 模型。目前,对于UML 活动图到马尔可夫链的转换,研究者参考较多的还有文献[9]中基于构件转移图将UML 活动图转换为马尔可夫链模型的方法。本文基于构件转移图将图2 的无人车变道活动图转换为DTMC 模型,利用该模型对无人车变道行为的可靠性进行预测。图9 为图2 所对应的构件转移图。其中,CTGStart 为起始节点,CTGend1和CTGend2为终止节点。在DTMC 模型中增加了终止状态C 和失效状态F。状态C 表示系统功能成功完成,状态F 表示系统发生失效。图10 为图9 对应的DTMC 模型。将构件转移图转换为对应的DTMC 模型时,还要在每条转移边上乘以源端模块的可靠性。这里需要指出的是,本文中对感知模块和LSTM 模块的故障传播概率基于错误渗透率进行了计算,故图10 中以感知模块为源端的转移边将不是直接乘以感知模块的可靠性P0,而是乘以P0+ (1-P0)(1-PC1)。

Fig.8 Reliability prediction value图8 可靠性预测值
将由图10 中DTMC 模型得到的PRISM 代码及式(7)输入到模型检测工具PRISM 中。由PRISM 模型检测工具得无人车变道可靠性的值约为90.19%。

通过图6 和图10 中的DTMC 模型进行可靠性预测时,得到的值分别为76.47%和90.19%。基于构件转移图思想构建DTMC 模型时,只能对使用到的模块进行概述,并没有描述实际运行时模块的使用情况,粒度细化能力较差。根据预测结果对比可知,基于构件转移图思想所得的可靠性预测值明显更高,该方法没有考虑到在无人车变道时对各模块的具体使用情况。根据映射规则所得的DTMC 模型在粒度细化方面的能力更强,更适用于无人车变道可靠性预测。

Fig.9 Component transfer图9 构件转移

Fig.10 DTMC corresponding to component transfer diagram图10 构件转移图对应的DTMC
6 结语
无人车的可靠性对于道路安全至关重要。本文对无人车变道过程进行建模,对无人车变道功能的可靠性进行预测。考虑到LSTM 神经网络具有鲁棒性,感知模块输出故障不一定会渗透到LSTM 模块的输出,通过错误渗透率可以对模块间的故障传播概率进行计算,使得可靠性信息更加准确。本文分别对利用UML 活动图映射所得的DTMC 和基于构件转移图所得的DTMC 进行可靠性预测,实验结果表明基于映射规则所得的DTMC 模型在粒度细化方面的能力更强。无人车可靠性预测结果可以体现无人车变道性能好坏,从而为设计人员提供了是否需要改良的参考。实际的无人车变道过程可能面临着十分复杂的情况,本文的UML 建模粒度较粗,这也是未来需进一步改进之处。

