毫米级颗粒在湍流场中的传热及着火特性
吴玉新,郭慧娜,冯乐乐,胡振坤, 张守玉
(1.清华大学 热科学与动力工程教育部重点实验室,北京 100084;2. 中国矿业大学 安全工程学院,江苏 徐州 221116;3. 上海理工大学 能源与动力工程学院,上海 200093)
固体燃料在热气流中的着火是其燃烧中的重要过程,该过程中,燃料颗粒的着火受多种因素影响,包括煤种、颗粒尺寸、加热方式等,除此之外,颗粒所在的气流环境(自然对流或强迫对流)对其着火过程也具有重要影响。LIU等在竖管炉内,研究了不同的对流强度对粒径约1.5 mm的大同烟煤温升历程、着火延迟时间和着火机理的影响,发现气相速度增大,升温速率明显增加,着火提前。KHATAMI等在落管炉内,研究了在自然对流和强迫对流情况下不同煤阶的煤粉着火机理,发现相对于自然对流,强迫对流使煤颗粒的升温速率变慢、着火延迟时间延长。虽然在不同的试验台上得出了相反的试验结果,但该结果进一步表明,燃料颗粒在热气流中升温至着火点的过程在颗粒整个燃烧历程中占据了很大一部分,准确预测颗粒受热及温升过程,对研究燃料颗粒着火特性和着火稳定性、燃烧工况优化具有重要意义。
随着双碳目标的提出,利用生物质与煤耦合发电成为燃煤电厂大规模减少CO的最可行措施,由于生物质破碎困难,目前生物质颗粒粒径一般为毫米级,其燃烧过程与微米级颗粒有较大区别。而流化床燃煤锅炉中的燃料受热及燃烧过程中,也是毫米级煤颗粒在强湍流密相床中发生受热与着火。
以往研究一般通过试验和数值模拟研究毫米级大颗粒燃料的燃烧过程,试验设备为热重分析仪、落管炉、平面火焰法和单颗粒反应器等,只能提供低雷诺数下的升温和着火环境,即关注层流条件或低脉动流场中大粒径燃料颗粒的燃烧特性。随着对高效、环保燃烧技术的重视,具有高速射流特征的低氧稀释燃烧技术[11-12]日益得到重视,被认为是新一代高效洁净的燃烧技术。该技术中,实际炉膛内部是一个具有强湍动度、火焰拉伸率的环境,燃料颗粒如煤、生物质等在其中受热及燃烧。强湍流脉动的流场特征对固体燃料颗粒的传热、着火及燃烧均具有重要影响。在气体燃料燃烧研究中发现,流场的湍流脉动会使火焰面变得褶皱,从而增大火焰面积,在一定范围内增大湍流燃烧速度。在固体燃料的燃烧中,湍流脉动通过破坏固体颗粒的热边界层对颗粒边界的气相传热传质起强化作用。
考虑粒径效应时,由于大粒径颗粒的弛豫时间较长,对湍流涡中的大尺度含能涡团具有较强的响应,由于微米级小粒径颗粒的弛豫时间与湍流涡中Kolmogorov时间接近,具有较好的弥散性和倾向跟随性。因此湍流对大颗粒燃料传热的作用更显著,需要研究湍流对大颗粒燃料着火过程的影响。但目前相关试验研究仍非常有限,湍流强化气体和液体传热传质试验中,典型的试验方法有射流火焰法、对冲火焰法、对冲风扇法。射流火焰法通过提高来流速度以增加脉动速度,这意味着较大的脉动速度需要较高的时均速度,难以区分强迫对流与湍流脉动的影响。对冲火焰法通过在中间平均速度接近0的滞止面上研究湍流脉动对气体传质的影响,但同样需要较高的来流速度以达到所需的脉动速度。对冲风扇法是通过设计风扇对冲流动在空间中心形成平均速度接近0的均匀各向同性湍流区域,在此区域内研究湍流脉动对液体燃料液滴蒸发、气体火焰传播等的影响。BIROUK等对称布置8个风扇,通过在立方体的8个角放置8个风扇构建可控的湍流流场,并进行各向同性湍流测量验证,并开展了湍流强度、液滴粒径、温度压力等对液滴蒸发的系统研究,该方法的优势是脉动速度大小可直接由风扇转速调控,操作简单高效。
由于受到环境温度的限制,已有研究尚无法开展针对毫米级固体燃料颗粒在强湍流场中的传热及着火的试验。为此,笔者搭建了宽温度范围下的四风扇对冲湍流试验装置,开发了流场及颗粒温度的测量方法。在不同湍流强度下,观测烟煤颗粒的着火现象。为了区分湍流强化传热与传质,利用粒径4.4 mm的铜球颗粒在高温湍流环境下开展湍流强度对颗粒传热特性的试验研究,并提出了考虑湍流强化作用的单颗粒受热修正关联式,采用粒径2 mm的铜球颗粒进行验证,进一步明确了湍流对毫米级煤颗粒着火过程的促进作用。
1 试 验
1.1 试验台与测量装置
搭建的各向同性湍流试验台如图1所示,由排气系统、电炉加热系统、风扇系统、颗粒给样系统、激光测量系统及数采系统等部分组成。其中湍流电炉内腔为八棱柱,竖直截面为正八边形,其内切圆直径为200 mm。经设计与校验,炉内最高加热温度可达900 ℃。电炉的前后门为开关式,且在中部开有观察窗,用于高速相机拍照;左右两侧壁面开设激光通道。电炉内对称布置4台相同的风扇,叶轮直径为70 mm。每台风扇的转速由单独的变频器控制,最高安全工作转速可达8 000 r/min,借助风扇转动在炉子中央构建各向同性湍流流场。试验过程中,单颗粒铜球/煤样由刚玉管和热电偶丝固定,并通过给样系统送至电炉中央。电炉内部流场特性由粒子图像测速仪(PIV)协同连续激光器进行测量,颗粒温度采用K型热电偶和无纸记录仪。采用Omega K型热电偶,不确定度为±2.2 ℃或测量值的0.75%。PIV测量主要误差来自示踪粒子的位置,经估计相对误差为±1%。煤颗粒的着火时间通过高速拍照识别,对应时间误差为0.1 s。
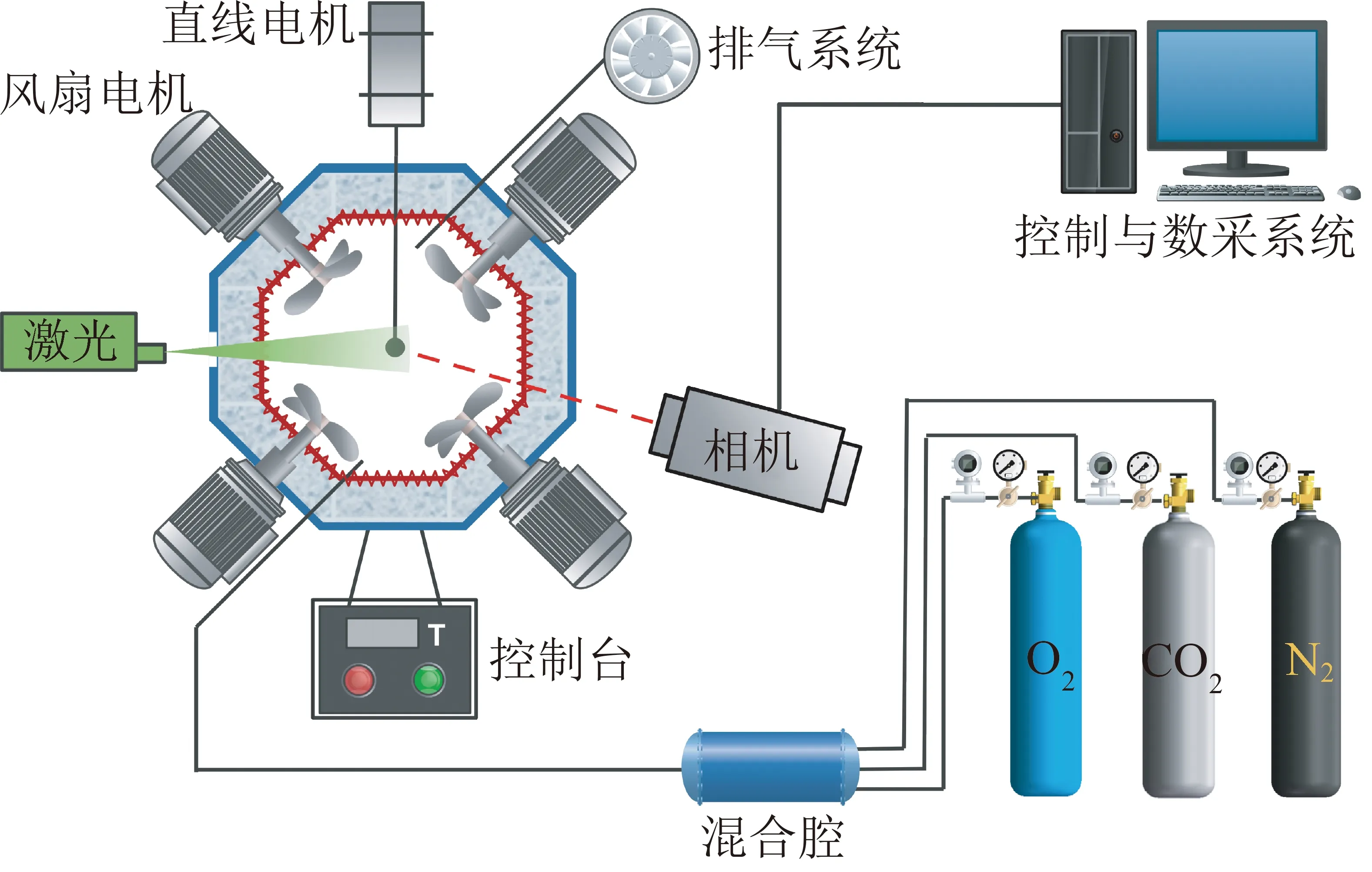
图1 均匀各向同性湍流试验台示意Fig.1 Schematic diagram of the homogeneous and isotropic turbulence experimental setup
采用高速相机对无单颗粒煤/铜球的流场进行拍摄及流场特性分析,拍摄区域为炉膛中间20 mm × 14 mm。试验过程为:① 根据试验工况调整4台风机的频率至相应转速,同时向流场中均匀散布示踪粒子;② 打开连续激光器,使激光照亮所拍摄区域的示踪粒子;③ 打开高速相机调整相机距离激光面的距离,选用适当的镜头焦距、光圈值,设置拍摄频率及相机的曝光时间;④ 将拍摄的粒子图像传输至计算机,采用TSI公司的Insight 4G处理软件,根据连续的两帧间的示踪粒子位移计算局部的流场速度。试验设备的主要参数见表1。
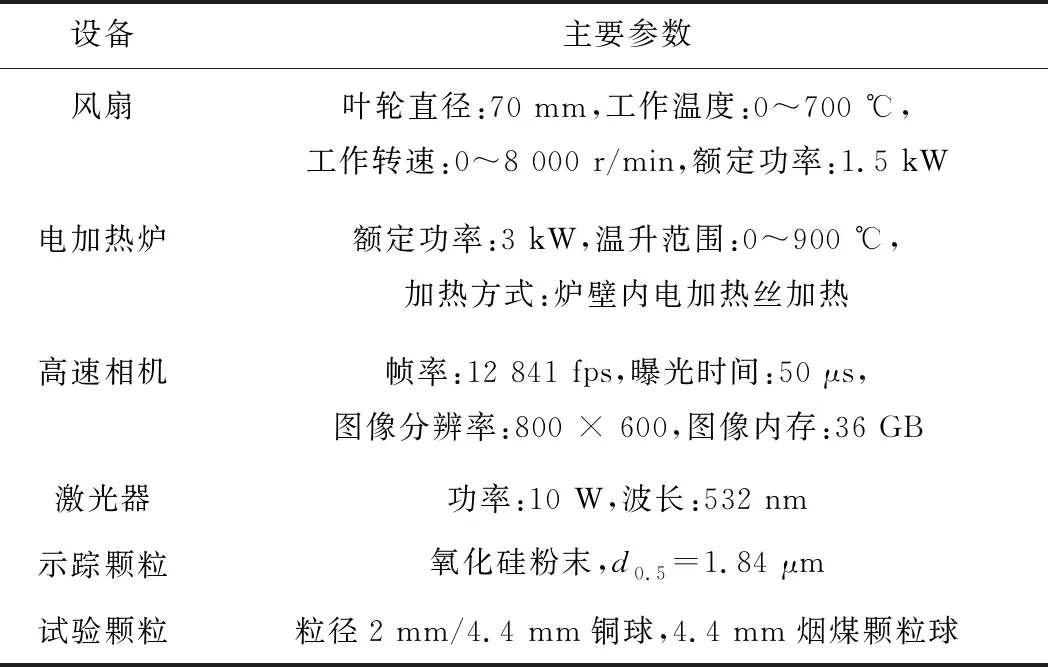
表1 试验设备及主要参数
1.2 试验工况与数据处理方法
PIV流场4台风扇转速变化为1 000~4 000 r/min。通过Insight 4G软件后处理可得到拍摄区域内任一坐标点下沿,方向的瞬时速度,。
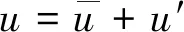
(1)
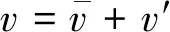
(2)
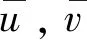
时均速度分量计算公式为
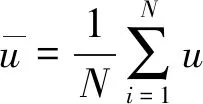
(3)
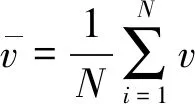
(4)
式中,为图像对的个数。
为分析脉动速度在不同工况流场中的差异,采用均方根计算脉动速度分量,即
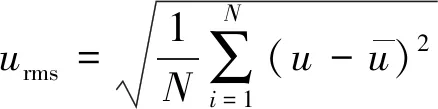
(5)
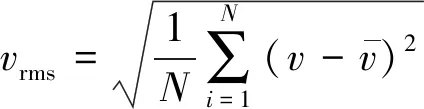
(6)
式中,,分别为沿,方向的均方根速度,即对测量平面上的脉动速度分量进行时间平均。
时均脉动速度即湍流强度Vel计算公式为
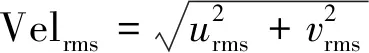
(7)
利用式(3)~(7)可计算拍摄区域内每一点的平均速度与脉动速度,可用于流场特性分析以及计算颗粒雷诺数等。
在湍流中,流场的均匀性指时间平均湍流量与空间位置无关,即在每个位置的值相同;各向同性指湍流的统计平均性质与空间的方向无关,湍流量在任何给定位置的所有方向上均相同,如=。为了量化均匀性与各向同性的程度,定义均匀性指数、各向同性率的计算公式为
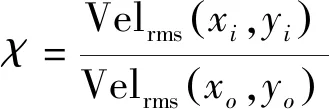
(8)
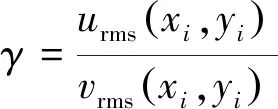
(9)
其中,(,)为区域中心位置坐标;(,)为区域的其他位置坐标。通过计算拍摄区域的,即可表征流场的均匀性与各向同性。
铜球升温测量工况见表2。由于不同粒径的颗粒升温趋势基本一致,因此升温试验采用2种代表性粒径的铜球:一种为粒径4.4 mm的铜球,升温范围100~500 ℃,根据其升温结果开发湍流强化传热的模型;另一种为粒径2.0 mm的铜球,其升温结果用于湍流强化传热模型的验证。

表2 铜球升温测量工况
2 试验结果与分析
2.1 湍流流场特性分析
图2为各转速下沿,方向流场的平均速度和脉动速度分布。可以看出,随着转速由1 000 r/min增至4 000 r/min,脉动速度逐渐由0.8 m/s增至3.2 m/s,平均速度由0.1 m/s增至0.6 m/s,且流场的脉动速度随风扇转速线性增加,各风扇转速下的脉动速度均远高于平均速度。流场分析结果与文献[20-22]一致,试验中可通过改变转速来改变流场的湍流脉动强度。
图3为转速2 000 r/min下流场的均匀性指数和各向同性率的空间分布云图,中心虚线圆环表示后续升温和着火试验中单颗粒位置,由于坐标比例尺的原因这里显示为椭球形,而实际上试验颗粒为球形。可以看出,试验颗粒所在的流场区域均匀性指数约为1,由于远离中心,气流不对称,流场的非均匀性增加;各向同性率在1.0~1.2波动。
从流场特性分析看,试验系统虽存在宏观平均速度,但远低于脉动速度,同时炉内中心位置流场具有良好的均匀性与各向同性,这使得研究湍流脉动对颗粒传热的促进作用成为可能。因此,可以认为试验在近似均匀各向同性湍流条件下进行。
图4为炉内中心处在不同转速下,沿,轴方向的瞬时速度,以及沿着45°方向瞬时速度的概率密度函数。可以看出,各转速下,3条曲线几乎重合,说明风扇转速的变化不影响炉内流场的均匀性。
2.2 湍流强度对铜球颗粒升温的影响
为进一步研究湍流对传热的作用,并区分传热与传质,采用粒径为4.4 mm的铜球,在不同炉温和转速下进行颗粒升温试验(图5),每个工况重复3次,重复性良好。可以看出,风扇转速一定时,随着炉温升高,升温速率加快。为了分析湍流强度对升温速率的影响,计算了炉温为100 ℃时,不同转速下铜球的升温速率(图6(d))。炉温一定时,在快速升温阶段,随着转速的提高,即湍流强度提高,铜球的升温速率加快。对于某一确定时刻,低转速时,如0~1 000 r/min,升温速率的变化对风扇转速的增大较为敏感;高转速时,如2 000~3 000 r/min,继续提高转速,升温速率变化不大。这是由于风扇转速增加,从气相到颗粒表面的传热增强,从而颗粒温度升高,同时也减小了颗粒内部和气相的温差,较小的温差降低了颗粒内、外热量的传递,即对升温速率的增大产生“负反馈”效应。转速越高,该作用越明显。因此在高转速下,继续增大转速,虽然湍流脉动速度增大,但相同时刻升温速率的增量变化不大。
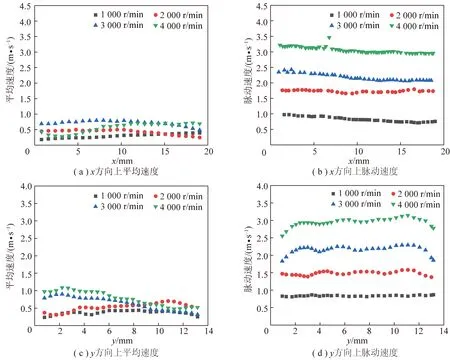
图2 不同转速下流场的平均速度与脉动速度分布Fig.2 Mean velocity and fluctuating velocity distribution of the flow field observed for different rotation speeds
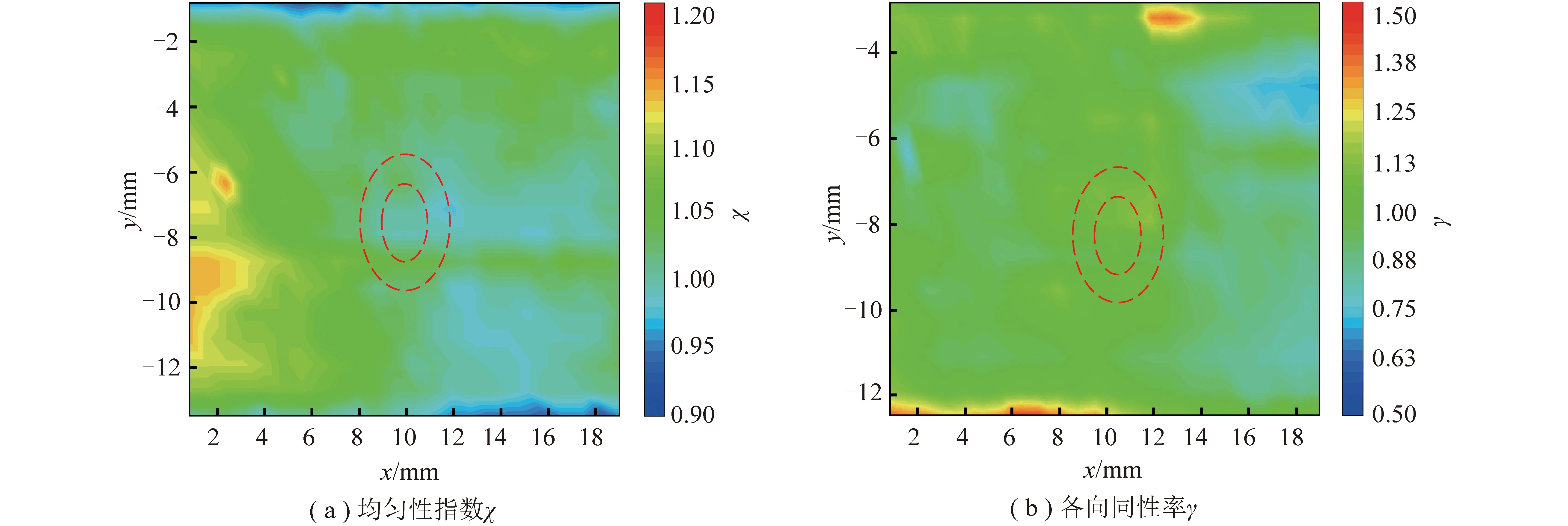
图3 流场的均匀性指数与各向同性率分布云图(2 000 r/min)Fig.3 Spatial distribution of the homogeneity index and isotropy index observed for a rotation speed of 2 000 r/min
2.3 湍流强化颗粒传热模型
基于流场测量结果和颗粒升温结果,可建立湍流强化颗粒传热的模型。
对于粒径4.4 mm铜球,其毕渥数≪0.1,因此可采用集总参数法进行分析。假定着火前未反应发生,颗粒受热来自炉壁的热辐射和气相与固相之间的传热。根据经典的颗粒加热零维模型,颗粒的升温速率可表示为
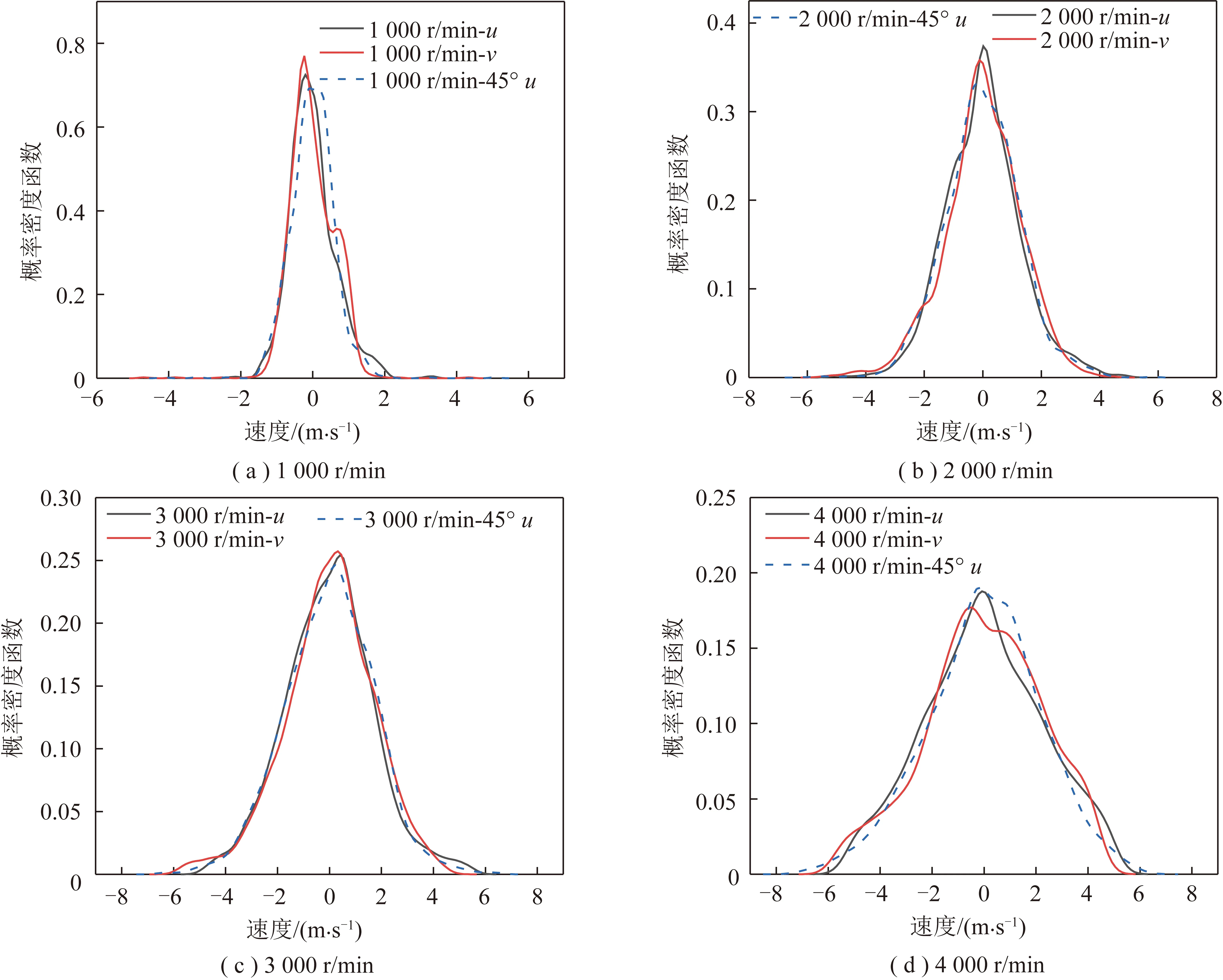
图4 不同转速下瞬时速度的概率密度函数Fig.4 Probability density functions of velocity for various fan speeds
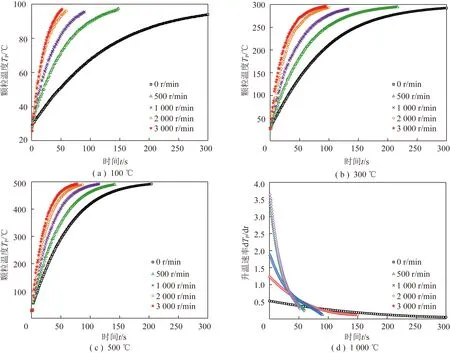
图5 不同温度、不同风扇转速下4.4 mm铜球的升温结果Fig.5 Heating results of a 4.4 mm copper ball at different furnace temperatures and fan speeds
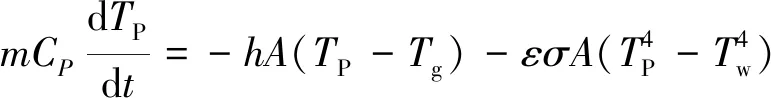
(10)
式中,为颗粒质量,kg;为颗粒定压比热,J/(kg·K);为颗粒表面积,m;为颗粒温度,K;为气体温度,K;为辐射壁面温度,K;为发射率;为对流换热系数,计算公式如式(11)所示;为玻尔兹曼常数。
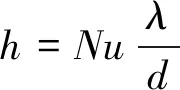
(11)
式中,为努谢尔数;为铜球直径,m;为流体的导热系数,W/(m·K)。
以往关于煤颗粒升温着火以及热解研究中,一般只考虑流场的对流作用对升温的影响,并采用经典的Ranz-Marshall公式计算。
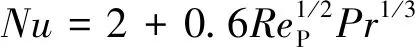
(12)
其中,为颗粒雷诺数,计算公式为
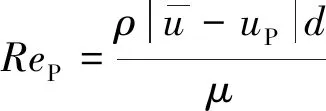
(13)
式中,为气体密度,kg/m;为颗粒速度,m/s;为气体黏度,Pa·s。
利用式(10) ~(13)计算不同粒径铜球颗粒在不同转速下的升温曲线,并与试验升温曲线进行对比,如图6所示。由图6可以看出,风扇转速为0 (即不存在气体脉动速度)时,利用式(12)计算的与试验值较为一致;风扇转速为500~3 000 r/min(即存在气体脉动速度)时,计算值明显小于试验值,且这种偏差随着脉动速度的增加而增大。通过对比不同粒径铜球的升温结果可以看出,颗粒粒径越大,不考虑湍流脉动速度带来的计算偏差越大,说明湍流对促进大颗粒的传热作用更明显。图7为利用Ranz-Marshall公式计算的与根据试验结果反推值对比,可以看出,这种偏差是由于只考虑对流作用而不考虑气体脉动作用时的计算值(即传热系数)远小于实际值。
湍流强脉动存在的情况下,忽略气体速度的脉动对单颗粒传热的促进作用将带来较大的温度偏差。这是因为忽略气体脉动将使计算得到的小于实际值,因此需要对的计算方法进行修正。
由于试验系统存在较小的宏观平均速度,仍需用Ranz-Marshall公式计算强迫对流对颗粒传热的作用。为了比较湍流与层流对传热影响效果的异同并保证公式的简洁性,考虑仍采用Ranz-Marshall公式的形式计算,并在此基础上进行修正。
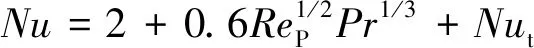
(14)
其中,为气体的脉动速度对传热的作用。查阅文献可知,目前尚无关于的计算公式,但有学者为了提高Ranz-Marshall公式的计算精度,采用引入额外因子的方法对其进行修正。参考其中的方法,可表示为
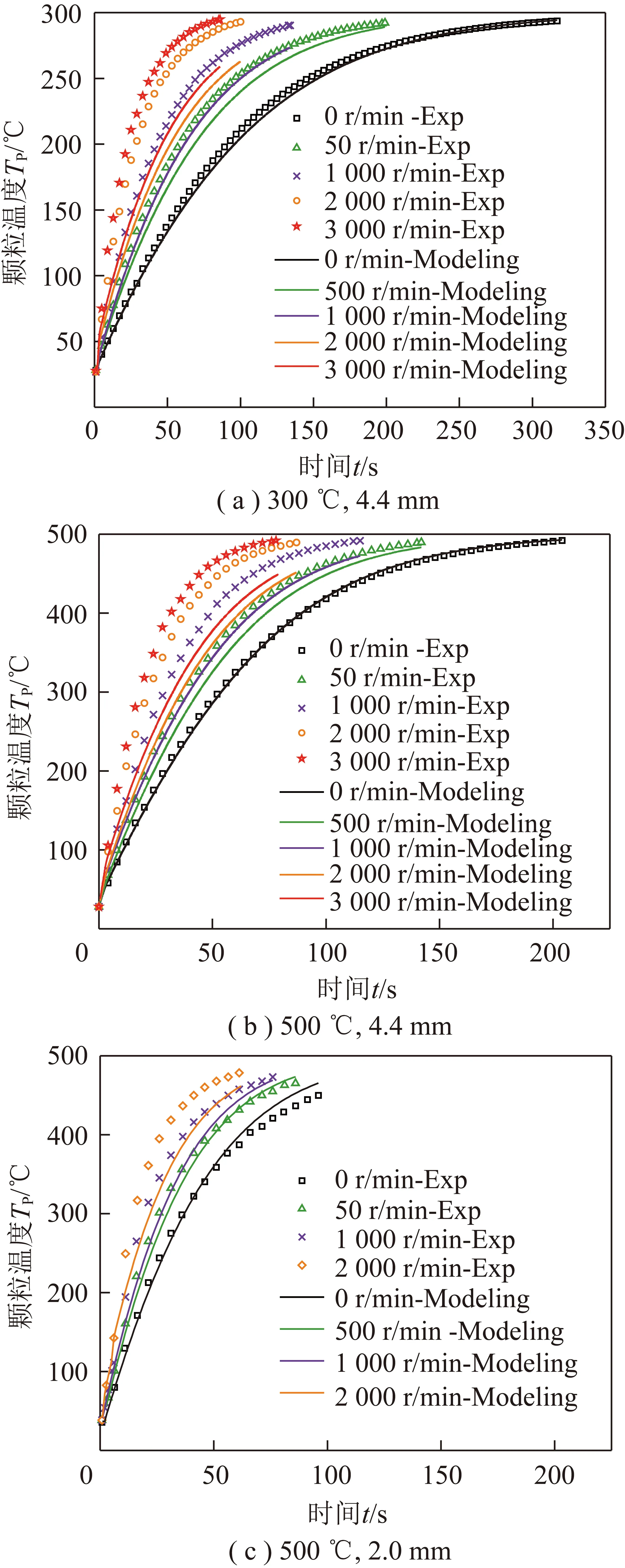
图6 不考虑气体脉动时预测的铜球升温结果Fig.6 Predicted heating result of copper ball without considering turbulent fluctuating velocity
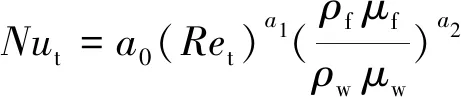
(15)
其中,为颗粒湍流雷诺数,以脉动速度计算;下标f,w分别为流体和壁面;,和为待确定的系数。基于4.4 mm铜球颗粒的试验数据,按照多元线性回归理论可求得,和的推荐值分别为 -2.346 5,1.318 9,-4.112 3,代入式(14)~(15)可得以上拟合关联式在试验范围内有效,其中>1。事实上,很多学者试验研究了湍流条件下管流中的壁面传热特性,文献[30-31]表明,在强湍流条件下,表达式中雷诺数的指数大于1,最高可达1.96。因此,式(16)中颗粒雷诺数的指数大于1是合理的。此外,通过引入()表示湍流脉动对热边界层中热物性不均匀的影响。以上结果表明湍流强化毫米级颗粒传热的原因主要因为湍流对壁面边界层的破坏。

(16)
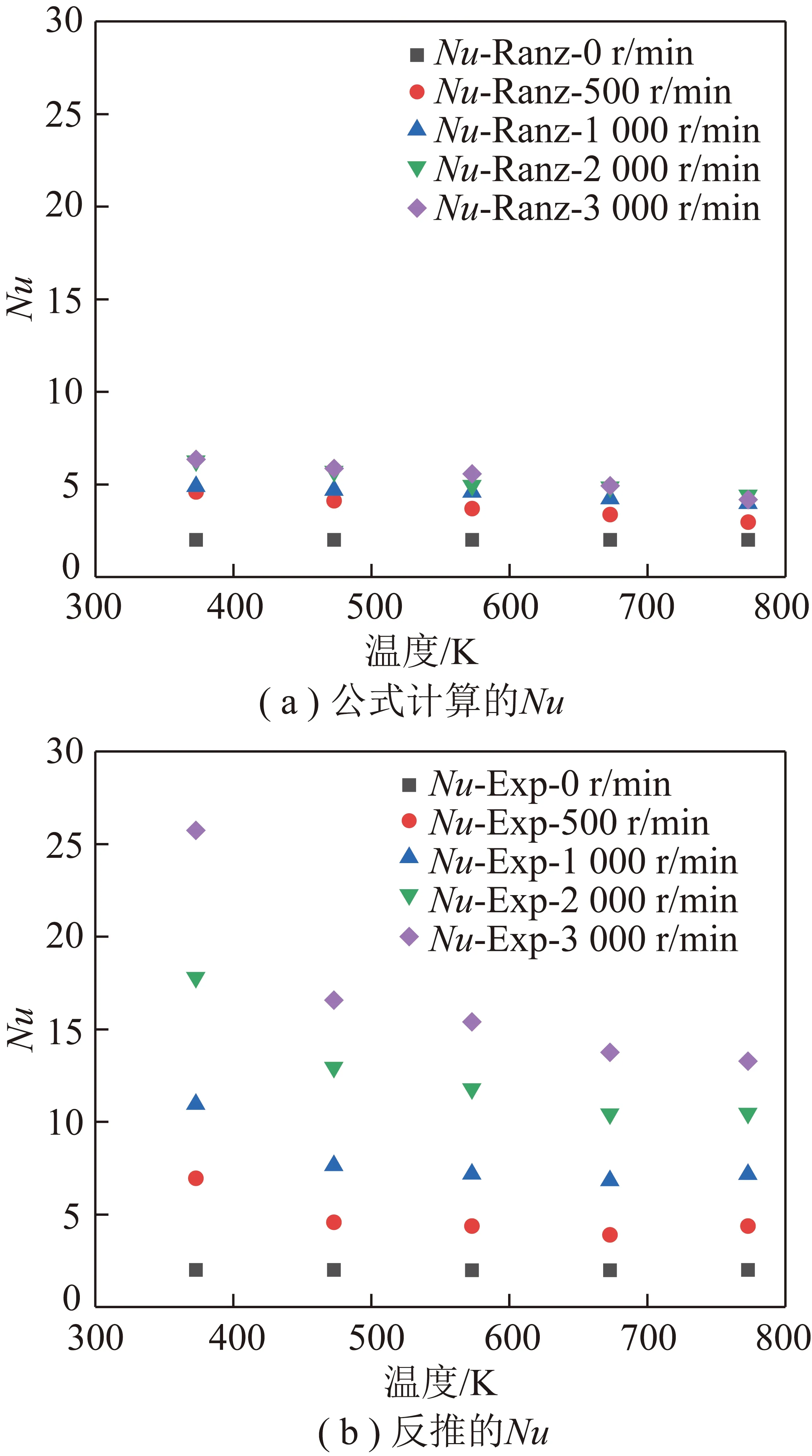
图7 Nu的计算值与根据试验结果反推值对比Fig.7 Comparison of Nu number calculated correlation and experimental results
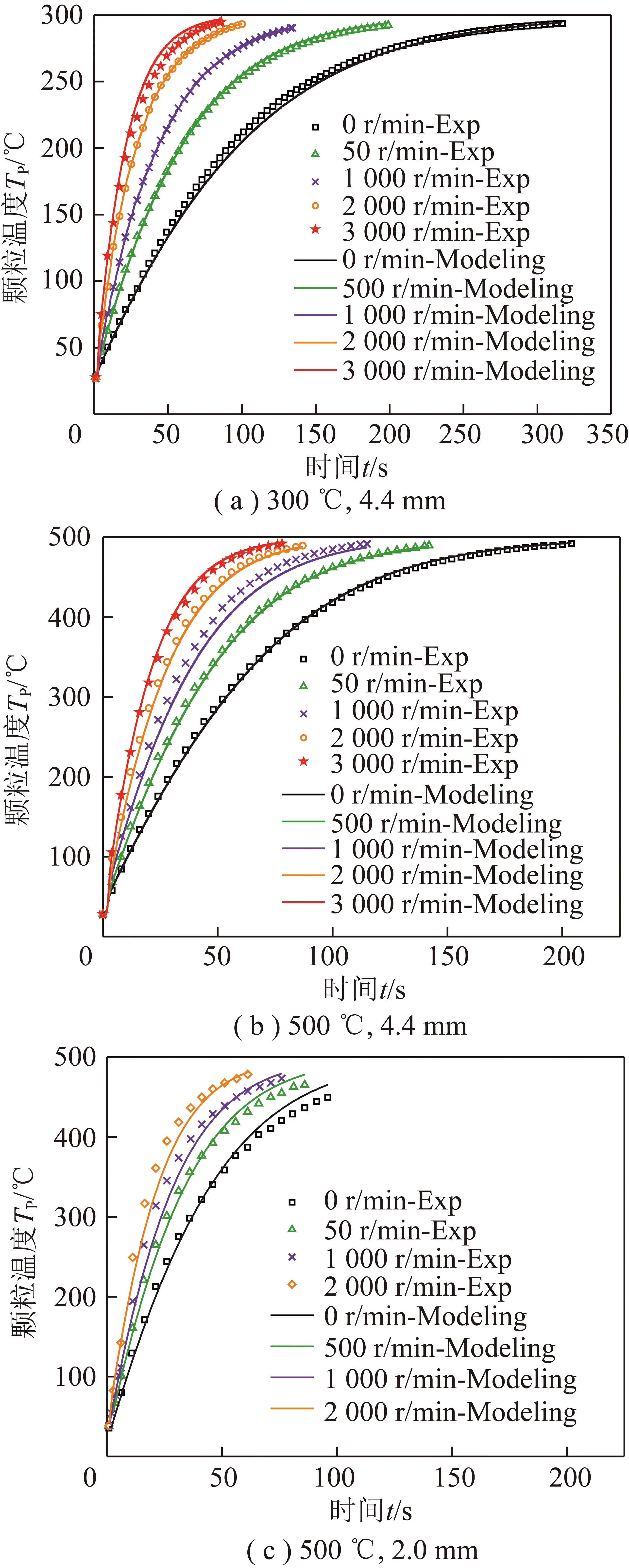
图8 考虑气体脉动时预测的铜球升温结果Fig.8 Predicted heating results of copper ball considering turbulent fluctuating velocity
将该传热模型应用于零维模型,预测不同粒径、炉膛温度、炉膛转速下的颗粒升温,如图8所示。可以看出,模型预测结果与的试验结果非常接近。因此,通过在经典的Ranz-Marshall对流换热关联式中添加湍流作用项,并借助试验数据确定模型参数,可描述湍流脉动对颗粒传热的作用。
2.4 湍流强度对煤颗粒着火的影响
在炉温为500 ℃时,研究粒径为4.4 mm的左云烟煤颗粒在不同的风扇转速下的着火试验,高速相机拍摄的典型时刻照片如图9所示。由图9可以看出,风扇转速为0 时,在44 s煤颗粒着火,反应主要在表面发生;风扇转速为1 000 r/min时,在30 s时煤颗粒着火;风扇转速为2 000 r/min时,在15 s时煤颗粒即发生着火。在煤颗粒燃烧过程中没有观察到明显的挥发分火焰,这是由于炉膛温度为500 ℃时,煤颗粒处于低温燃烧状态。根据着火结果可知,提高风扇转速即提高湍流脉动速度,可强化大粒径煤颗粒的传热过程,促进煤颗粒升温着火。

图9 不同转速、不同时刻的煤颗粒照片Fig.9 Photos of coal particles at different speeds and at different moments
深入分析风扇转速提高促进煤颗粒升温着火的原因,需要分析湍流脉动对传热传质2方面的影响。一方面,随着风扇转速增加,颗粒的湍流雷诺数增大,由式(16)可知,随之增加,说明湍流脉动增加提高了气固两相之间的传热系数,促进了气相向颗粒的传热过程;另一方面,根据传热和传质的可比拟性,扩散系数也随之增大,保证了颗粒表面有较多的氧气以及挥发分能较快析出,促进了颗粒着火。对于小粒径如微米级煤颗粒,也可参考本文的研究方法修正传热模型,以准确计算湍流脉动对其升温着火的影响。需要指出的是,微米级煤颗粒在湍流场中倾向于颗粒群燃烧,湍流作用通常表现在亚网格尺度,因此相对小,且微米颗粒的扩散作用增强,的影响显著降低。
3 结 论
(1)炉膛中心附近的流场可近似为均匀各向同性湍流,其平均速度远小于脉动速度,且脉动速度随风扇转速线性增加。
(2)随着风扇转速增加,煤颗粒着火提前,铜球颗粒的升温速率加快。湍流脉动速度增大明显促进气相向颗粒相的传热过程。
(3)在强湍流环境下,湍流对传热的强化作用不可忽略,且颗粒粒径越大,湍流对颗粒传热的强化作用越明显。
(4)在传热过程中,通过在经典的Ranz-Marshall公式中引入湍流作用项,建立湍流强化颗粒传热模型,可准确表征湍流脉动对颗粒传热的强化作用。
[2] DAVINI P,GHETTI P,BONFANTI L,et al. Investigation of the combustion of particles of coal[J]. Fuel,1996,75(9):1083-1088.
[3] TOGNOTTI L,MALOTTI A,PETARCA L,et al. Measurement of ignition temperature of coal particles using a thermogravimetric technique[J]. Combustion Science and Technology,1985,44(1/2):15-28.
[4] ESSENHIGH R H,MISRA M K,SHAW D W. Ignition of coal particles: A review[J]. Combustion and Flame,1989,77(1):3-30.
[5] KATALAMBULA H,HAYASHI J I,CHIBA T,et al. Mechanism of single coal particle ignition under microgravity condition[J]. Journal of Chemical Engineering of Japan,1997,30(1):146-153.
[6] LIU B,ZHANG Z,ZHANG H,et al. An experimental investigation on the effect of convection on the ignition behaviour of single coal particles under various Oconcentrations[J]. Fuel,2014,116:77-83.
[7] KHATAMI R,STIVERS C,LEVENDIS Y A. Ignition characteristics of single coal particles from three different ranks in O/Nand O/COatmospheres[J]. Combustion and Flame,2012,159(12):3554-3568.
[8] RIAZA J,GIBBINS J,CHALMERS H. Ignition and combustion of single particles of coal and biomass[J]. Fuel,2017,202:650-655.
[9] YANG Y B,SHARIFI V N,SWITHENBANK J,et al. Combustion of a single particle of biomass[J]. Energy & Fuels,2007,22(1):306-316.
[10] LU H,IP E,SCOTT J,et al. Effects of particle shape and size on devolatilization of biomass particle[J]. Fuel,2010,89(5):1156-1168.
[11] 李鹏飞,米建春,DALLY B B,等. MILD燃烧的最新进展和发展趋势[J]. 中国科学:技术科学,2011,41(2):135-149.
LI Pengfei,MI Jianchun,DALLY B B,et al. Progress and recent trend in MILD combustion[J]. Sci. China Tech. Sci.,2011,41(2):135-149.
[12] 黄文仕,吴玉新,冯乐乐,等. 高速圆射流中典型非球形颗粒的扩散特性[J]. 清华大学学报(自然科学版),2020,60(6):485-492.
HUANG Wenshi,WU Yuxin,FENG Lele,et al. Dispersion characteristics of typical non-spherical particles in a high-speed round jet[J]. Journal of Tsinghua University (Science and Technology),2020,60(6):485-492.
[13] SUN Z Y,XU C. Turbulent burning velocity of stoichiometric syngas
flames with different hydrogen volumetric fractions upon constant-volume method with multi-zone model[J]. International Journal of Hydrogen Energy,2020,45(7):4969-4978.
[14] GOULIER J,CHAUMEIX N,HALTER F,et al. Experimental study of laminar and turbulent flame speed of a spherical flame in a fan-stirred closed vessel for hydrogen safety application[J]. Nuclear Engineering and Design,2017,312:214-227.
[15] WANG L P,MAXEY M R. Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence[J]. Journal of Fluid Mechanics,2006,256:27-68.
[16] AHMED S,MASTORAKOS E. Spark ignition of lifted turbulent jet flames[J]. Combustion and Flame,2006,146:215-231.
[17] 夏朝阳,韩省思,毛军逵. 基于FGM的湍流射流扩散火焰超大涡模拟[J]. 工程热物理学报,2021,42(2):529-533.
XIA Zhaoyang,HAN Xingsi,MAO Junkui. Very large eddy simulation of turbulent jet diffusion flame based on FGM[J]. Journal of Engineering Thermophysics,2021,42(2):529-533.
[18] ZHOU B,FRANK J H. Experimental study of vorticity-strain interactions in turbulent premixed counterflow flames[J]. Proceedings of the Combustion Institute,2021,38(2):2909-2916.
[19] COPPOLA G,CORITON B,GOMEZ A. Highly turbulent counterflow flames: A laboratory scale benchmark for practical systems[J]. Combustion and Flame,2009,156(9):1834-1843.
[20] BIROUK M,FABBRO S C. Droplet evaporation in a turbulent atmosphere at elevated pressure:Experimental data[J]. Proceedings of the Combustion Institute,2013,34(1):1577-1584.
[21] VERWEY C,BIROUK M. An experimental assessment of the enhancement of fuel droplet vaporization in a very high turbulence intensity environment[J]. Proceedings of the Combustion Institute,2021,38(2):3243-3250.
[22] VERWEY C,BIROUK M. Fuel vaporization: Effect of droplet size and turbulence at elevated temperature and pressure[J]. Combustion and Flame,2018,189:33-45.
[23] BIROUK M,CHAUVEAU C,SARH B,et al. Turbulence effects on the vaporization of monocomponent single droplets[J]. Combustion Science and Technology,1996,113(1):413-428.
[24] 邢江宽. 煤粉与生物质热解和燃烧的高精度数值模拟研究[D]. 杭州:浙江大学,2020:20-24.
Xing Jiangkuan. High-fidelity simulation of devolatilization and combustion of coal and biomass [D]. Hangzhou:Zhejiang University,2020:20-24.
[25] 孙丽. 大颗粒燃料传热特性研究[D]. 北京:中国石油大学(北京),2019:22-25.
SUN Li. Numerical study on heat transfer characteristics of large fuel particles[D]. Beijing:China Petroleum University,Beijing,2019:22-25.
[26] RANZ W. Evaporation from drops[J]. Chemical Engineering Progress,1952,48(3):141-146.
[27] FISZDON J K. Melting of powder grains in a plasma flame[J]. International Journal of Heat and Mass Transfer,1979,22:749.
[28] LEWIS J A,GAUVIN W H. Motion of particles entrained in a plasma jet[J]. AIChE Journal,1973,19(5):982-990.
[29] LEE Y C,PFENDER E. Particle dynamics and particle heat and
mass transfer in thermal plasmas. Part Ⅲ. Thermal plasma jet reactors and multiparticle injection[J]. Plasma Chemistry and Plasma Processing,1987,7(1):1-27.
[30] OWHAIB W,PALM B. Experimental investigation of single-phase convective heat transfer in circular microchannels[J]. Experimental Thermal and Fluid Science,2004,28(2):105-110.
[31] SYED IZ,MUKHERJEE A. Experimental study of forced convection
heat transfer of water in a short microduct at a turbulent reynolds number[J]. Heat Transfer Engineering,2012,33(2):97-108.

