基于层次分析法的卓越师范生培养质量评价数学模型

程宏，王晓峰

（闽南师范大学 数学与统计学院，福建漳州 363000）

教育部2018 年9 月发布了《关于实施卓越教师培养计划2.0 的意见》[1]，针对当前师范生在培养方式、目标定位、师资保障、实习实践、考核方式等方面存在的问题，提出分类推进的指导意见.国家“十四五”规划中也指出，全社会要建立高水平的现代教师教育体系，建立健全教师教育评价制度和评价机制，力争到2035 年形成具有实践型特色的高水平教师人才培养体系[2-5].

20 世纪70 年代，美国匹茨堡大学教授、运筹学家Satty 提出了一种简单、灵活且实用的多准则决策方法——层次分析法(Analytic Hierarchy Process,AHP)[6].该方法的优点是利用较少的定量信息(主要是建立各指标层之间判断矩阵)建立决策思维过程，从而能为多目标、多准则的复杂决策问题最终提供一种简便的决策方法和数学模型[7-11].比如，对于三层决策问题，设第一层只有1个目标，第二层和第三层分别有m和n个因素，且第二层m个因素A1,A2,…,Am对第一层的权向量为a1,a2,…,am，第三层n个指标B1,B2,…,Bn对第二层因素Aj的层次单排序为b1j,b2j,…,bmj，则第三层B1,B2,…,Bn对第一层的层次总排序分别为，即第三层第i个因素Bi对总目标的权值为.宋阳和佟延秋[12]利用层次分析法研究了学生微格教学评价的数学模型，通过该模型对学生的师范技能做出科学的判断.董占明和左光纪[13]试用层次分析法建立一个评价高校学生成绩的数学模型以全面反映学生的综合素质.张军芳等人[10]运用层次分析法对师范生已有教育实习体系标准进行了数学建模分析，对师范生的实习中各个环节因素进行量化分析，对各项指标进行了层次总排序和一致性检验，分析结果对今后的教育实习和学生提升教育教学技能都有一定的指导和借鉴意义.

本文从定量分析的角度研究卓越师范生数学教师人才培养质量评价体系的构建，通过层次分析法分析各级指标层对师范生培养质量总目标的影响，提出改进卓越师范生培养质量的建议和措施，为健全师范生人才培养工作、提高师范生培养质量奠定基础.

1 卓越师范生培养质量评价指标体系层次结构的建立

师范类专业认证标准主要从践行师德、学会教学、学会育人、学会发展四个方面阐述了对毕业生的培养目标.借助于师范专业认证标准，结合数学学科特点，制定卓越师范生数学人才培养标准体系，详见表1.

表1 卓越师范生数学教师人才培养标准考核指标体系

在表1中，将卓越师范生人才培养标准指标体系按照层次结构划分为三个层次：第一层是目标层，用O表示；第二层是准则层，包含6个一级评价指标，用A（ii=1,2,…,6）表示；第三层是子准则层，共给出26个二级评价指标，用B（jj=1,2,…,26）表示.

2 层次分析法模型的建立

2.1 判别矩阵与权向量

在层次分析法中，同一层中的各项指标对上一层的贡献程度不是均等的，带有不同的权重.一般地，设第k层某项的总成绩y由第k+1 层的n项成绩x1,x2,…,xn来确定，则有y=，其中：ωi是第i项的权重，0 <ωi<1且=1.为确定权系数ωi，我们采用了成对比较，即从x1,x2,…,xn中任取两项xi和xj比较它们对y的贡献程度.按照Saaty评价尺度表示[7]，可按以下标度给赋值：若aij=1，则认为xi与xj对目标的贡献程度相同；若aij=3，则认为xi比xj对目标的贡献程度稍强；若aij=5，则认为xi比xj对目标的贡献程度强；若aij=7，则认为xi比xj对目标的贡献程度明显的强；若aij=9，则认为xi比xj对目标的贡献程度绝对的强；若aij=2,4,6,8，则认为xi与xj对目标的贡献程度处于两个相邻等级之间.若元素xi与xj对目标的贡献程度之比为aij，则元素xj与xi对目标的贡献程度之比为

根据上述评价模型评价指标体系层次结构，采用Saaty评价尺度法构造判别矩阵

矩阵G的唯一特征根λ对应的特征向量ω就是各因素对目标的影响权向量，即有Gω=λω.

2.2 计算判断矩阵的最大特征根及特征向量

2.3 对判断矩阵进行一致性检验

计算一致性指标CI=，其中n为判断矩阵的阶数，令CR=，称CR为随机一致性比率，其中RI表示平均随机一致性指标，具体取法：当阶数n依次取1,2,…,9时，RI分别取为0,0,0.52,0.89,1.12,1.26,1.36,1.41,1.46，如果判别矩阵G所对应的随机一致性比率CR能够充分小，在具体运算中，通常认为小于0.1，则可判别矩阵G是充分接近一致阵的，其λmax对应的特征向量ωmax可近似作为权向量.

3 层次分析法模型的求解

3.1 构建判断矩阵

准则层Ai对目标层O权重的判断矩阵记为OAi，子准则层Bj对准则层Ai权重的判断矩阵记为AiBj.为较客观准确的判断各子准则层对准则层的权重，我们在我校数学与应用数学师范专业2018级和2019 级学生中进行了问卷调查，问卷调查采用“问卷星”网络填报方式进行，共收到有效问卷360份.我们采用统计分析方法对各指标权重进行了数据处理，按照Satty 提出的标度法，我们建立如下七个判断矩阵：

3.2 判断矩阵一致性检验

按照层次分析法，对上述7个判断矩阵逐一进行一致性检验，验证各自随机一致性比率是否小于0.1.对于矩阵OAi，先计算矩阵OAi每一行指标元素的积，即

Gi=[5040,15,1,0.033333,0.014286,0.027778]T，计算Gi的n次方根

=[4.1407,1.5704,1.0000,0.56730,0.49259,0.55032]T，接下来对向量进行归一化，得ω=[0.49760,0.18872,0.12017,0.068174,0.059196,0.066134]T，则ω为所求特征向量，计算矩阵OAi的最大特征值λmax=6.6055，然后进行一致性检验[15]，则

所以可以认为判断矩阵OAi具有满意的一致性.

对于矩阵A1Bj，每一行指标元素的积Gi=[0.75,20,0.066667]T，计算Gi的n次方根=[0.90856,2.7144,0.40548]T，归一化后得ω=[0.22554,0.67381,0.10065]T，计算矩阵A1Bj的最大特征值λmax=3.0858，则

所以可以认为判断矩阵A1Bj也具有满意的一致性.对剩余的五个判断矩阵A2Bj,A3Bj，A4Bj，A5Bj和A6Bj做同样的计算，可得如下一致性检验，详见表2.

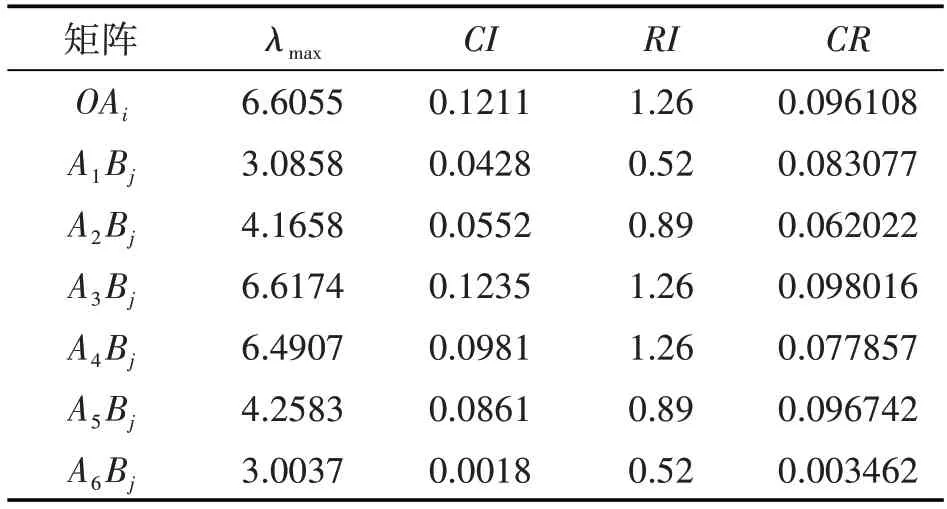
表2 卓越师范生数学教师人才培养标准考核指标一致性检验

从表2可以看出，7个层次单排序的CR值均小于0.1，该7个层次单排序都通过一致性检验.

3.3 层次总排序及其一致性检验

由表2 可知，单层次的权重排序比较单一，不能从整体上全面对卓越师范生数学教师人才培养标准考核指标进行分析.为此，还需要经过层次总排序，才能直观了解到所有的因素对于卓越师范生数学教师人才培养标准考核指标影响程度，构造成对比较矩阵进而得到权重及组合权重.考核指标层次排序详见如表3.

表3 卓越师范生数学教师人才培养标准考核指标层次总排序

层次总排序一致性指标为

层次总排序随机一致性指标为

从而可得层次总排序一致性比率为

因此，层次总排序的计算结果具有满意的一致性.

3.4 建立卓越师范生数学教师人才培养标准考核指标评价数学模型

根据计算出来的组合权重表3 中的组合权重系数的数据，设卓越师范生数学教师人才培养效果为Y，权重是目标层A的系数，目标层的各个指标为自变量y1,y2,…,y6，则构造出卓越师范生数学教师人才培养标准考核指标评价的数学模型为

若进一步考虑组合权重是子准则层B的系数，准则层的各个指标为自变量x1,x2,…,x26，则构建出更为细致的卓越师范生数学教师人才培养标准考核指标评价的数学模型为

4 模型的结论

根据表3 层次分析结果，可以看到卓越师范生数学教师人才培养效果指标体系中的权重按照数学学科知识(A1，0.49760)、教育、教学有关知识(A2，0.18872)、设计数学教学方案的能力(A3，0.12017)、实施教学方案的能力(A4，0.06817)、发现与解决教学问题的能力(A6，0.06613)、总结与反思教学过程的能力(A5，0.05919)顺序依次降低.数学学科知识(A1)占的比重几乎达50%，说明数学学科知识在卓越师范生的培养过程中更需要加强.数学学科知识中高等数学知识(B1)、中学数学知识(B2)、现代信息技术知识(B3)所占权重分别为0.22554、0.67381 和0.10065，可见对于师范专业毕业生来说，中学数学知识(B2)应该足够重视.

在教育、教学有关知识(A2)方面，教学案例性知识(B6)和数学教学法知识(B5)所占比重较高，分别为0.44855 和0.33537，这就要求在师范生培养方面对于案例性教学要十分重视，将数学教学法与案例式教学有机结合，用理论指导实践，用实践验证理论，使得卓越师范生的培养在看得见、感受得到、可操作的直观演示下能模仿、可实践，并且目标达成变得更为具体而直观.案例式教学在具体操作过程中采用同课异构的形式，也就是学生展示—教师点拨—教师展示的方式进行，通过对比差异，使学生身临其境，并且使学生在教师、学生身份的角色中自由转换，感受教育教学理论的可操作性以及优越性.

在设计数学教案的能力(A3)方面，教学目标的设计(B8)权重为0.41036，其次是学生认知特点与起点分析能力(B9)权重为0.18603，可以看出目标设定对于一节课的教学设计所起到核心的作用.教学目标相当于靶子，确定好目标才能有的放矢.教学目标的设计可以直接导向一节课的定位，在四基、四能、核心素养、育人价值方面如何设定，将直接决定教学的下限与上限以及教学质量的高低，所以在卓越师范生培养方面，使学生认识目标的重要性，并能制定出合理而高效的教学目标就成为日常教学的重点.

在实施教学方案能力(A4)方面，问题情境创设引入课题能力(B14)权重为0.40369，因为好的开端是成功的一半，学生学习的良好兴趣往往开始于课堂的伊始，从开始导课时就能抓住学生的注意力，让学生带着问题走进课堂，使他们的思维在课堂的有限时间内高速驰骋，有效提升学生的思维力，这是优质数学课堂的重要支撑点.而组织学生进行数学探究活动能力(B15)权重为0.25054，说明数学教学中探究性活动的开展对于学生学习数学的价值和意义非常巨大，因而在卓越师范生培养方面，对于导课中如何有效渗透四能的指导以及如何有效开展数学探究活动要有更多的侧重.

在总结与反思教学(A5)的过程中，对教学效果的反思(B22)的比重为0.45308.可见，教学效果有最显性的能直抵人心的存在感，透过教学效果反思，进行教学方案修正，这是最便捷的方式，其实教学目标达成的反思才是改变教学效果最根本的途径，但由于其内隐性师范生不容易察觉，所以在卓越师范生培养时，应有意识引导学生分析教学目标的反思，使学生的反思能够更全面改善、更加有效.

在发现与解决数学问题的能力(A6)方面，发现数学教学问题的能力权重为0.64833，说明大家普遍认可对于教学的改进首先来自于高度的教学觉察能力，只有意识到问题的存在才能更好地改进教学.

5 模型的应用

为检验所建立卓越师范生数学教师人才培养标准考核指标评价数学模型的效果，我们选取模型（5）作为研究对象，邀请6 位师范专业任课教师对2019 级“卓师班”学生进行打分，为公平期间，每位老师只负责其中一个指标的分数打分.我们从中随机挑选出10 位同学，分别以1 到10 编号，10 位同学的各项指标成绩如表4 所示.

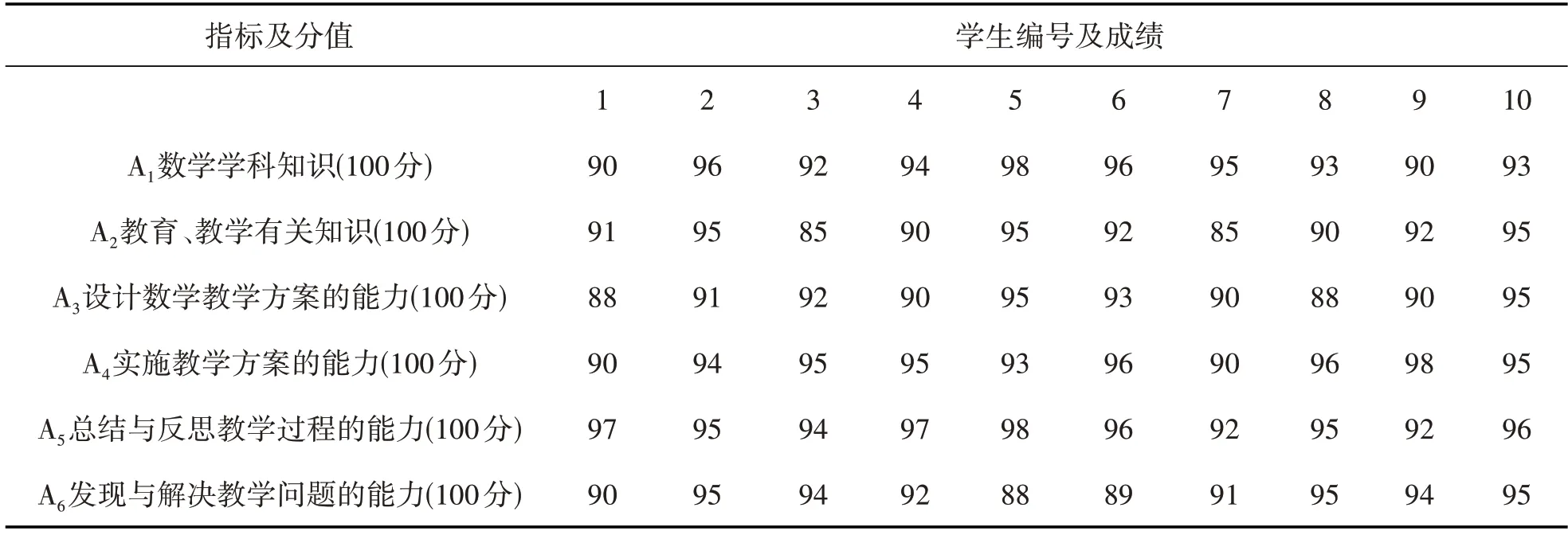
表4 数学与应用数学专业2019级“卓师班”十位同学考核分数

在表4中，共有6 个指标，每个指标赋值100分，按照以往求平均值的方法，我们可得这10位学生的得分依次为91分，94.3分，92分，93分，94.5分，93.6分，90.5分，92.8分，92.6分，94.8分，学生分数从高分到低分排序依次为10，5，2，6，4，8，9，3，1，7.按照模型（5），我们重新计算10 位学生分数，则依次为90.4分，94.9分，91.1分，92.8分，96.1分，94.4分，91.7分，92.3分，91.3分，94.1分，按照新的分数学生分数从高分到低分排序依次为5，2，6，10，4，8，7，9，3，1.从新的排名结果可以看出，编号为5 的学生数学学科知识的分数98分，由于该指标所占权重较大，直接导致了其排名第一的结果.在今后的教学实践中，我们将尝试将更为细致、更为全面的数学模型(6)进行卓越师范生培养质量的考核，使卓越师范生的素质得以全面提升.