PIVHFS 中计算关联决策专家权重的多属性群决策方法研究

朱国成 ,徐健 ,赵瑞华

(1.广东创新科技职业学院 科学技术协会，广东东莞 523960；2.云安中学生物组，广东云浮 527500)

0 引言

相较于犹豫模糊集(Hesitant Fuzzy Sets，HFS)，概率犹豫模糊集(Probabilistic Hesitant Fuzzy Sets，PHFS)由于考虑了决策专家对于隶属度的整体认可趋势，所以能够更加全面表达决策信息，概率犹豫模糊集自文献[1]定义以来，在理论与应用研究方面都获得了极大丰富与拓展.在理论研究方面，文献[2]不仅梳理了PHFS 的相关概念与性质，还定义了概率犹豫模糊偏好关系并初步研究了其一致性；为了减弱概率信息需要满足的条件，文献[3]借助证据推理的思想改进了PHFS 的定义；文献[4]在文献[2]的基础上进一步研究了概率犹豫模糊偏好关系.PHFS 的应用方面，国内外学者主要从解决决策问题的角度出发进行研究，例如，文献[5]利用概率犹豫模糊数(Probabilistic Hesitant Fuzzy Num⁃bers，PHFN)与理想值之间的关系提出了3 种决策算法，为研究智能系统与专家系统提供了不同的决策视角；文献[6]将改进的雷达图与信息数据的相似度理论进行结合，建立了一套概率犹豫模糊集多属性群决策(Probabilistic Hesitant Fuzzy Sets Multi-attribute Group Decision Making，PHFSMAGDM)算法，并成功解决了决策专家针对属性的偏好问题；文献[7]利用概率犹豫模糊加权Maclaurin 几何对称平均算子来解决PHFSMAGDM问题中的属性信息聚合问题，基于此建立的算法具有计算简单、灵活可靠且稳定性好等特点.目前在众多研究PHFS 理论与应用的文献中，鲜有学者考虑在PHFS 中隶属度对应的概率所关联的决策专家权重问题.事实上，PHFS 中隶属度发生的概率反映了决策群体的整体决策意向，与HFS 相比能够保留更多决策信息数据，所以在群决策问题中具有更多优势.但一个不容忽视的问题是，决策过程中对于决策专家的偏好时有发生，此时PHFS的定义中却没有包含该因素，故反应隶属度的重要性也就无从谈起.针对该问题，本文在PHFS 的基础上，重新定义了考虑决策专家权重的PHFS，同时，PHFN 中的隶属度值用区间数(Interval Num⁃ber，IN)刻画，此时新定义的PHFS 为考虑决策专家权重的概率区间值犹豫模糊集(PIV(W)HFS).在多属性群决策(MAGDM)问题中对本文定义的PIV(W)HFS 理论进行了验证分析，以此来说明在PIVHFS中考虑决策专家权重的必要性.

1 预备知识

定义1[7]记非空集合X，二元组H=｛〈x，hx（px）〉｜x∈X｝称为集合X上的PHFS，其中将

称为PHFE，PHFE中的γl表示元素x属于集合H的隶属度，pl为隶属度γl发生的概率，|h(p)| 表示PHFEh(p)中元素个数.

定义2记非空集合X，二元组H=｛〈x，hx（px）〉｜x∈X｝称为集合X上的PIVHFS，其中将

称a为区间数.若0 ≤a-≤a+，则a被称为正区间数；若a-=a+，则a退化为实数.

定义5[9]设a=[a-,a+],b=[b-,b+]为2 个正区间数，则有如下运算：

定义7[12]设2 个区间数a=[a-,a+],b=[b-,b+]，a,b的相离度用D(a,b)表示为

D(a,b) 越大，a，b相离的程度越大；特别地，当D(a,b)=0时，有a=b，即区间数a，b相等.

定义8令ai(i=1,2,…,n)为一组非负实数，且有r=1,2,…,n.若

则称（1）式为Maclaurin 对称平均算子，这里i1,i2,…,ir为遍历组合1,2,…,n中的一切r元组为二项式系数.容易验证Maclaurin 对称平均算子具有下列性质：

定义9在MAGDM 问题中，决策专家集Z={z1,z2,…,zl,…,zH}，其权重用ωzl(l∈{1,2,…,H}) 表示，且方案集A={a1,a2,…,ai,…,aM}(i∈{1,2,…,M})和G={g1,g2,…,gj,…,gN}(j∈{1,2,…,N})为属性集，属性权重用符号表示且未知，第l个决策专家给予第i个方案的第j个属性的评价信息用IN 信息数据表示，具体表示形式为本文研究的属性类型皆为效益型.根据定义9有如下定义：

定义10将由PIVHFS 构成的决策信息数据转换为PIV(W)HFS，其中

plij的计算方法采取文献[1]中的方法；

定义11根据定义10，PIVHFS 中的元素PIVHFE 及PIV(W)HFS 中的元素PIV(W)HFE 分别定义如下：

（3）式中的符号“⊂”类似与集合关系中所使用的包含符号“⊂”，因为等皆为IN，故不能直接用符号“⊂”描述IN之间的包含关系.

2 属性权重计算方法

根据属性之间信息数据差异程度来确定属性权重的方法——熵值法，该法为计算属性权重的主流方法之一.其算法具体步骤如下:

步骤1 由定义9 至定义11，将决策信息评价数据转换为PIV(W)HFS决策矩阵；

步骤2 根据定义12，计算各方案的属性综合值，即PIV(W)HFE()的综合值为

3 决策算法

由定义5可知，各方案ai的综合值|ai|仍为IN；

步骤5 利用定义6 对各方案ai的综合值|ai|进行两两测度，建立积型模糊互补判断矩阵

4 数值算例

教师教学水平的评价问题其实是一个MAGDM 问题，为了突出教师教学水平评价的公平性与专业性，针对某学科对教授该学科的所有老师进行评价.现有4 位教师(决策方案)需要被评教，用符号ai(i=1，2，3，4)表示，分别从教学态度(g1)、教学内容(g2)、教学方法(g3)和教学效果(g4)等4个因素(属性)进行评价，权重分别用(j=1,2,···,N)表示.评价主体由学生(z1)、教学督导(z2)、同事(z3)和学院领导(z4)组成(决策专家组)，其权重分别为=0.5、=0.25、=0.15=0.1，教学评价主体针对4 位教师教学水平的评分值经过技术处理以区间数表示（详见表1），并利用本文知识对4位教师教学水平进行排序.

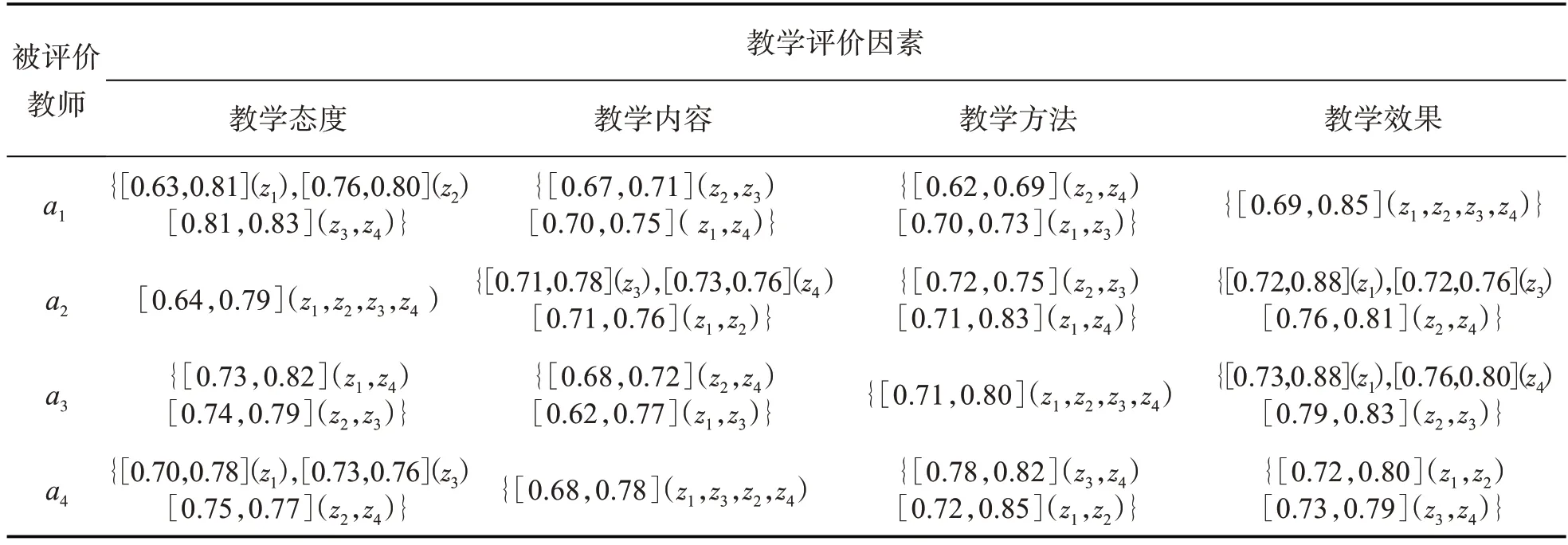
表1 教师教学评价评分表

4.1 计算属性权重

步骤1 根据定义11，将表1转换为PIV(W)HFS决策矩阵

步骤2 根据定义12 计算各方案的属性综合值分别为

步骤5 计算在属性gj上的熵值Sj与(j=1,2,3,4)分别为

4.2 算法步骤

由计算属性权重可知，步骤1、步骤2 已经完成，现直接进入步骤3.

在积型模糊互补判断矩阵[πii′]4×4中，πii′×πi′i≈1是在计算时四舍五入造成的；

步骤6 采用式（1）对πii′进行集结以获取各方案ai的比较结果||，分别为

4.3 算法比较

不考虑隶属度对应的概率所关联的决策专家权重,在PIVHFS 理论基础上设置一种MAGDM 算法，并将算法结果与考虑隶属度对应的概率所关联的决策专家权重算法结果进行对比.按照文献[1]中的方法，将表1 转换为由PHFS 构成的决策矩阵，如上文矩阵[Hij]4×4所示.

在定义9、定义10、定义11 与本文案例的基础上进行设置算法.同时为了能够与4.2 节中的决策算法结果更好比较，属性权重计算方法参考第2节内容，决策步骤参考第3 节内容，同时为了提高文章可读性，这里相关符号皆没有替换.

4.3.1 计算属性权重ωgj(j=1,2,3,4)

第1步：计算PIVHFE(hij)的综合值为

第2步：确定属性的理想属性值为

第3步：利用定义7，将PIVHFE(hij)的综合值与属性的理想属性值进行测度，建立相离度矩阵[dij]4×4，并采用文献[13]中的方法将相离度矩阵[dij]4×4规范化，得规范化矩阵[uij]4×4；

第4步：计算在属性gj上的熵值sj为

这里规定若uij=0，则uijlnuij=0；

第5步：求解属性gj的权重ωgj为

按照以上5步，可得各属性权重分别为

4.3.2 决策算法

第1步：根据定义9、定义10、定义11 及文献[1]，将决策信息表转换为由PIVHFE (hij)构成的决策矩阵[Hij]4×4；

第2步：由矩阵[Hij]4×4及属性权重计算方法确定属性权重ωgj（j∈{1,2,3,4}）；

步骤4：获取各方案ai的综合值|ai|为

由定义5可知,各方案ai的综合值|ai|仍为IN；

步骤5：利用定义6对各方案ai的综合值|ai|进行两两测度，建立积型模糊互补判断矩阵

步骤6：采用式（1）对πii′进行集结以获取各方案ai的比较结果||，并根据||大小对各方案进行排序，这里||大者其对应的方案ai为优.

根据以上算法步骤，无论r取何值(r=1，2，3，4)，皆可得各方案排序为a1≻a2≻a3≻a4.

5 结语

本文从PIVHFS 的定义出发，考虑了隶属度对应概率所关联的决策专家权重计算问题，并在此基础上建立了一套MAGDM 算法.数值算例结果表明，该算法操作简单，稳定性强，能够根据方案的信息数据快速取得排序结果.同时，在PIVHFS 中考虑决策专家权重前后所取得的决策结果差别较大.事实上，PIVHFS 中概率反应的是隶属度发生的整体发生可能性，兼顾到决策专家权重以后还体现了该隶属度发生的重要性，在决策案例中所能包含的信息更加全面，故排序结果说服力更强.在PIVHFSMAGDM 问题中，随着PIVHFE 中元素PIVHFN 的隶属度数量的增加，其概率信息在集结时快速衰减，怎样解决此类问题，今后需要进行深入研究.