腔磁杂化系统中磁振子阻塞的实现

欧孝飞, 李欣悦， 袁宁， 王楠， 朱爱东

(延边大学 理学院， 吉林 延吉 133002)

0 引言

近年来，单光子的相干操纵已经成为量子光学和量子信息处理领域的重要研究课题.目前，利用不同物理系统实现光子阻塞效应的研究已经取得较大进展，如在电路腔量子电动力学系统[1-2]、光子晶体-量子点系统[3]等系统中.近年来，将磁性材料中的自旋波量子(磁振子)作为量子信息载体的研究引起学者们的关注[4].目前，在腔磁系统中已观察到多种实验现象，如电磁感应透明[5]、磁子-光子-声子纠缠[6]等.本文提出了一个由2个相互耦合的微波腔和1个铁磁材料钇铁石榴石(YIG)球组成的杂化物理系统模型，并通过外加经典场来弱驱动磁振子实现了磁振子的阻塞效应.另外，通过对二阶关联函数和平均磁子数进行数值模拟，证明了该系统能够实现参数可控的单磁子反聚束效应.

1 系统模型与哈密顿量

图1 系统模型示意图

系统的哈密顿可以写成如下形式：

(1)

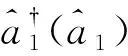
(2)

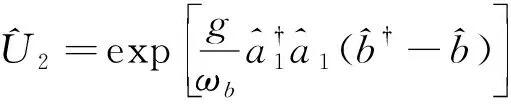
(3)

其中G=g2/ωb.在式(3)中，由于声子与腔之间的相互作用已经被解耦，因此在式中省略了声子的哈密顿项.由式(3)中的最后1项可以看出，光力耦合能够产生类克尔型的非线性作用.

2 磁振子的阻塞效应

2.1 磁振子的等时二阶关联函数

求解主方程即可获得磁振子的等时二阶关联函数.系统的主方程为：

(4)

(5)

当g(2)(0)<1时，磁振子呈现的是亚泊松分布；当g(2)(0)>1时，磁振子呈现的是超泊松分布；当g(2)(0)=0时，磁振子呈现的是完美的反聚束现象.

2.2 系统参数对磁振子阻塞的影响

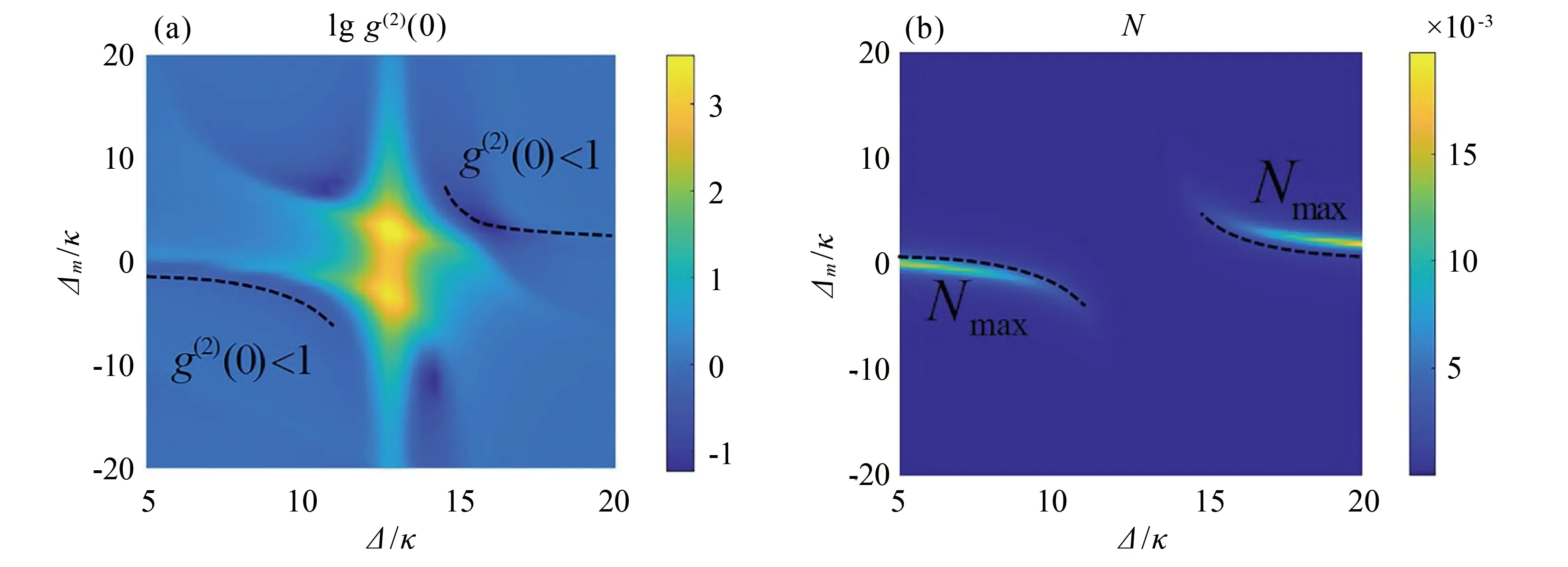
图2 二阶关联函数(a)和平均磁子数(b)随磁振子和腔失谐量的变化

2)两个腔之间的隧穿耦合强度和腔失谐量对磁振子阻塞的影响.取磁振子的失谐量Δm=5κ， 其余参数不变.由图3(a)可以看出：二阶关联函数存在一个最佳区域(图中黑色虚线区域).这说明，当产生最佳磁振子阻塞时， 2个腔之间的隧穿耦合与失谐量之间存在线性关系.当Δ=-10κ时，在J≈15κ处可获得磁振子的最佳反聚束效应.由图3(b)可以看出，在最低二阶关联函数的对应区域，磁振子具有较大的平均磁子数.由以上可知，通过调控隧穿耦合强度可以实现明亮的单磁振子阻塞状态.

图3 二阶关联函数(a)和平均磁子数(b)随腔失谐量和耦合强度J的变化

3)克尔型相互作用G和腔失谐量对二阶关联函数和平均磁子数的影响.图4为磁振子二阶关联函数随着非线性耦合强度G和腔失谐量Δ的变化情况.由图4(a)可以看出，二阶关联函数在Δ≈ -10κ附近处出现了反聚束现象，在G≈5κ时达到最佳，随后随着G的增加反聚束效应逐渐消失.出现上述现象的原因为：一是当光力耦合不断加强时，由左腔通过隧穿耦合转移到右腔的光子减少，使得右腔中的光子与磁振子的磁偶极耦合变弱；二是在外加激励的作用下磁振子被不断激发.在图4(b)，与图4(a)中二阶关联函数小于1对应区域(图中虚线对应的区域)的平均磁振子数均较大，并且磁振子数随着G的增加而增加.但当G达到15κ时，反聚束现象已变得很弱.

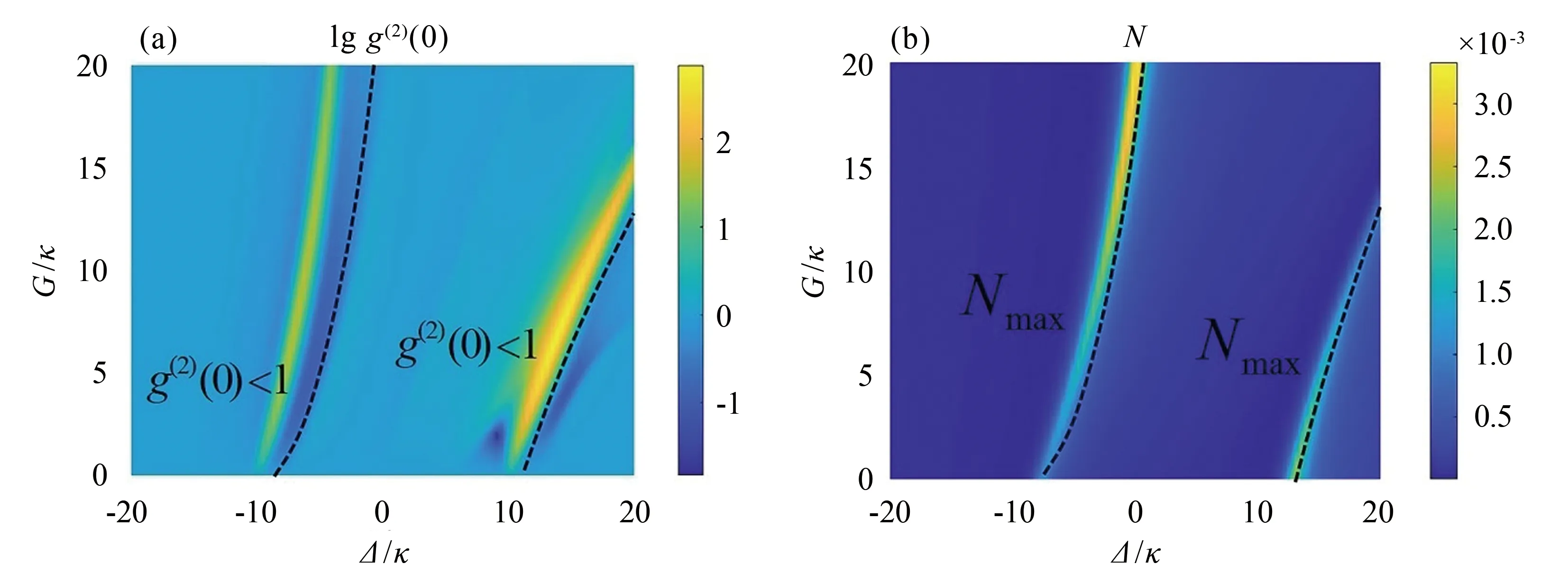
图4 二阶关联函数(a)和平均磁子数(b)随非线性耦合强度G和腔失谐量的变化

4)磁振子与腔之间的磁偶极耦合强度对二阶关联函数的影响.由图5可以看出，发生磁振子阻塞的区域其对应的平均磁振子数也较大(图5(b)中虚线所示的Nmax区域).由此可知，当腔失谐量固定时，可以通过调节YIG球的位置改变耦合强度λ， 即由此可以实现磁振子阻塞.

图5 二阶关联函数(a)和平均磁子数(b)随耦合强度λ和腔失谐量的变化

3 结论

本文研究了杂化腔磁系统中磁振子的反聚束效应，并通过求解主方程和数值模拟得到了磁振子的二阶关联函数和平均磁振子数随系统参数的变化规律.本文研究表明，通过调节机械模与腔之间的耦合、腔的失谐量、磁振子与腔的耦合等参数可实现较为明亮的磁振子阻塞状态.本方案可为在杂化系统中实现单磁子源以及量子信息处理提供参考.