基于空间相关电离层模型的天波雷达目标跟踪
郭 振 王增福 兰 华 潘 泉
(西北工业大学自动化学院 西安 710129)
(信息融合技术教育部重点实验室 西安 710129)
1 引言
天波超视距雷达(Over-The-Horizon Radar,OTHR)通过电离层反射效应来突破雷达视距的限制[1],可实现对隐身飞机、大中型舰船、洲际导弹、巡航导弹等高价值目标的远程预警,是最经济、费效比最高的远程预警手段。在目标跟踪中,天波雷达目标跟踪算法需执行雷达坐标系到大地坐标系的坐标变换。考虑到天波雷达信号经电离层反射,坐标转换过程中电离层参数(例如电离层虚高)是必需的。电离层参数的不准确是天波雷达目标定位误差的主要来源[2]。为了提高天波雷达的目标定位精度,需要采用更精准的电离层建模以及相应的电离层估计算法和目标跟踪算法。按照天波雷达目标跟踪方法对电离层虚高的假设,将其分为以下两类。
第1类方法将每层电离层虚高假设为确定性常数。其基本思路是将现有数据关联方法拓展到多路径数据关联,在雷达坐标系下完成量测预测及目标-量测-模式的三元关联,然后实现地理坐标系下的航迹更新。该类方法同时采用多路径量测数据更新航迹,提高了原始量测信息利用率,具有较好的估计性能。在该类假设下,学者分别提出了多路径概率数据关联方法(Multipath Probabilistic Data Association, MPDA)[3],基于期望最大化的联合多路径数据关联和状态估计方法[4],基于随机有限集统计理论的方法[5,6],多路径线性多目标综合概率数据关联算法[7],融合前向接收机量测的方法[8]以及基于分布式期望最大化的联合优化目标状态估计、多路径数据关联和电离层虚高辨识的方法[9]。
第2类方法中将每层电离层虚高假设为单个随机变量,在目标跟踪及状态估计过程中考虑电离层虚高误差的影响。Rutten等人[10]假设电离层虚高服从线性动态演化的形式,其过程噪声为高斯分布,并提出了一种多假设多路径航迹融合算法。基于同样的假设,Lan等人[11]提出了一种基于消息传递方法的天波雷达量测级融合方法。Pulford[12]假设每层电离层虚高服从已知均值和方差的单变量高斯分布,提出了一种用于不确定坐标配准的多路径概率数据关联算法(Multipath Probabilistic data association for uncertain Coordinate Registration, MPCR)。文献[13,14]假设电离层虚高是已知量和未知时变偏差的组合,考虑了目标状态和电离层虚高偏差的联合估计。
上述现有的方法都将每层电离层虚高看成固定或随机的单个变量,但由于电离层状态是一个复杂时空过程,在一个较大的区域中,每层的电离层虚高在不同位置显然不同。而随着目标位置的变化,天波雷达信号在电离层中的反射位置也是变化的。上述方法对电离层虚高位置独立性的假设大大简化了天波雷达目标跟踪算法的设计,但这种简化显然会带来电离层参数不准确的问题。
大量研究表明电离层状态参数是空间相关的,特别是在总电子含量和电子密度方面。早期学者发现电离层在空间上水平相关[15],后来学者从电离层在纬向和经向的相关性[16]、电离层日变率在水平和垂直方向的相关性[17]、电子密度的空间协方差模型及其在纬度和经度方向上不同的相关长度[18],以及电离层相关性在剖面扫描成像中的应用[19,20]等方面进行了研究论证。
基于上述研究工作,本文提出一种随位置变化且考虑空间相关性的电离层模型,应用于天波雷达目标跟踪。该电离层模型可以更精确地表示天波雷达目标跟踪中的电离层参数,从而达到减小天波雷达目标定位误差的目的。与前面提到的天波雷达目标跟踪方法一样,本文仍将电离层虚高作为坐标变换的参数。假定电离层虚高随位置变化是自然成立的。同时,电离层虚高的空间相关性假设是基于上述的关于电离层总电子含量和电子密度的空间相关性研究,以及电离层虚高对他们的依赖关系。例如,在给定天波雷达工作频率时,电离层虚高与抛物线层模型中电子密度最大值的高度呈线性关系[21]。
在实践中,为了实时在线估计电离层虚高,需要部署电离层探测仪[22]。但是由于客观因素限制,电离层探测仪仅能部署于可用区域,且需要付出相应的运营成本,因此只能在有限的位置获得电离层参数的量测值,而这些位置不一定是天波雷达和目标之间反射信号的位置。根据空间相关性,未量测位置的电离层参数可以通过有限的量测推断得到,从而提高电离层参数估计精度并改善天波雷达定位精度。
本文考虑电离层的空间相关性并将电离层虚高建模为高斯马尔可夫随机场(Gaussian Markov Random Field, GMRF),第2节给出模型与问题描述,讨论新的电离层虚高建模方法。之后在第3节提出基于电离层虚高GMRF模型的多径天波雷达目标跟踪算法,接下来在第4节进行仿真验证,最后给出结束语。
2 模型与问题描述
在本节中,首先给出目标运动和天波雷达量测模型,同时指出电离层虚高是从雷达量测中反演目标状态的关键参数。之后讨论了电离层虚高具体建模方法,最后在所有模型的基础上描述了本文拟解决的问题。
2.1 目标运动模型

2.2 天波雷达量测模型
假设电离层为球面模型,包含E层和F层[3],雷达信号存在4种单跳传播模式:EE(即发射过程中通过E层反射到目标,接收过程中通过F层从目标反射回接收机,下同),EF, FE和FF。与文献[3]相同,假定通过每个模式接收到的雷达信号都可能独


2.3 电离层虚高高斯马尔可夫随机场模型
由于天波雷达广阔的监视区域,可能反射天波雷达信号的电离层区域也较大;同时由于地球磁场特性,大范围内的电离层虚高不能视为一个整体,因此需要考虑其随位置的变化。基于现有的电离层空间相关性研究[15,18],简略起见,本文仅考虑电离层虚高在水平方向的相关性。短时间内,不同位置之间的电离层虚高的相关性取决与它们之间的距离,这对应于局部马尔可夫性质[23],因此电离层虚高被建模为马尔可夫随机场。参考文献[19,20]中假设电子密度和电子总量是高斯的,同样地,本文假设电离层虚高也是高斯的。综上所述,本文采用离散GMRF来描述E层和F层的虚高。
以E层为例来说明电离层虚高向量hE的GMRF建模,为了简便下文将向量hE下标省略。将电离层区域A离散化为N个子区域集合,则向量h中元素个数为N。将虚高向量h与一个无向图G=(V,E)关联起来,其中V={1,2,...,N}是图中点的集合,E是图中边的集合(i,j),i,j ∈V且i/=j。记虚高向量h中的元素hi ∈R+且i ∈V为E层子区域i的电离层虚高。
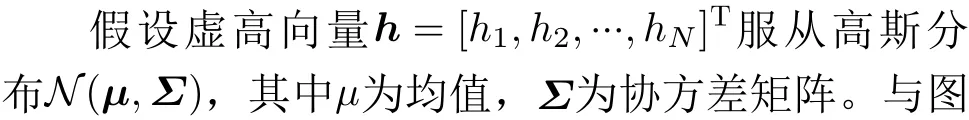

2.4 问题描述
对于天波雷达每个扫描时间帧内,GMRF模型下的天波雷达目标跟踪问题可以分为两部分:第1部分为推断电离层虚高的后验均值和协方差;第2部分为基于前文中的目标动态模型、推导的电离层虚高的后验统计量和雷达量测模型,计算目标状态的最小均方误差估计。
3 基于高斯马尔可夫随机场的天波雷达目标跟踪算法
本文将新提出的电离层虚高的GMRF模型嵌入到MPCR[12]算法中,形成名为MPCR-GMRF的新算法。GMRF先验从电离层的历史数据中得到。局部的确定区域的实时电离层量测通过电离层探测仪提供。一旦接收到新的电离层实时量测,未测量子区域的电离层虚高的后验均值和方差可以通过GMRF模型推断得到,然后该统计量被目标跟踪器使用,以得到目标状态估计。
3.1 电离层虚高推断
为了叙述方便,以E层为例来说明未测量区域的电离层虚高推断,并略去向量hE下标。2.3节提出的模型中将电离层区域A离散化为子区域的集合。在每帧k中,将该子区域集合划分为子集α和β,分别代表未被测量的电离层子区域和其余子区域。为了推断未测量区域的电离层虚高,将E层N个电离层子区域的虚高向量h及其相应GMRF参数势向量η和精度矩阵Q划分为
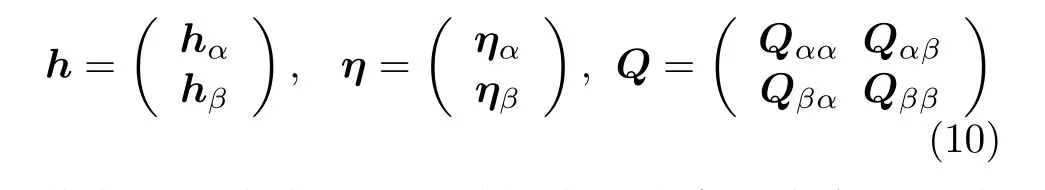
其中,hα为未测量区域的未知电离层虚高,hβ为测量区域的已知电离层虚高。

3.2 目标量测预测
量测预测是MPCR算法中目标状态估计过程不可缺少的。相比于MPCR算法,由于电离层模型不同,MPCR-GMRF算法有新的量测预测模块。结合3.1节电离层虚高推断,MPCR-GMRF算法目标量测预测的计算过程总结在表2的算法中,以下为具体计算。


表2 量测预测及其协方差

3.3 目标存在模型



3.5 目标状态估计

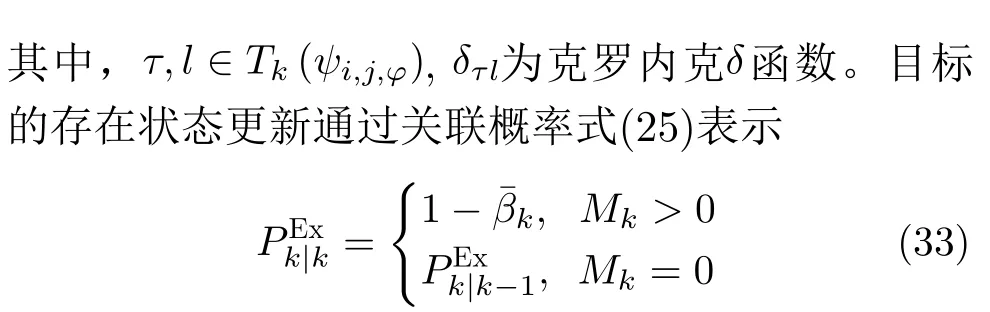
4 仿真
本文新提出MPCR-GMRF算法通过MATLAB R2018b实现并验证,电脑配置为Inter(R) Core(TM) i5-5300U CPU@2.3 GHz。仿真中将MPCRGMRF与天波雷达经典跟踪算法MPCR[12]和MPDA[3]作对比。3种算法的统计结果基于400次蒙特卡洛实验。本文采用文献[19]中的方法在2维经纬度空间中构造1阶近似GMRF的精度矩阵Q,构造的E层和F层的Q阵的值见表3。仿真场景中电离层虚高的真实值从构造的GMRF模型中采样得到。表3给出了天波雷达和电离层的参数设置。

表3 仿真场景参数设置
图1为仿真场景设置示意图。天波雷达接收机在原点位置,标记为方块,天波雷达发射机在离接收机距离为100 km的X轴上,标记为菱形。假设目标在X-Y平面内匀速直线运动,其运动轨迹如图1中蓝色线段所示,目标运动状态转移函数写为f(xk)=F xk,其中状态转移矩阵F=[F′0;0 F′],F′=[1T;0 1],T为采样时间间隔。目标初始状态假设为[1100 km 0.15 km/s 0.09472 rad 1.52665×10—4rad/s]T。假设有两部实时电离层探测仪分别部署在编号为1和73的电离层子区域,在图1中由黑色实心圆表示。在目标运动过程中,天波雷达信号在反射到目标和从目标反射回天波雷达的过程中用到的电离层子区域根据式(34)和式(35) 计算,这些区域同时在图1中分别由绿色和红色六角形标记。假设电离层区域A在X-Y平面的离散化如图1虚线所示。电离层子区域的大小记为ΔX×ΔY。表1中的下标it和ir计算为

表1 式(2)中传播模式与电离层参数的对应
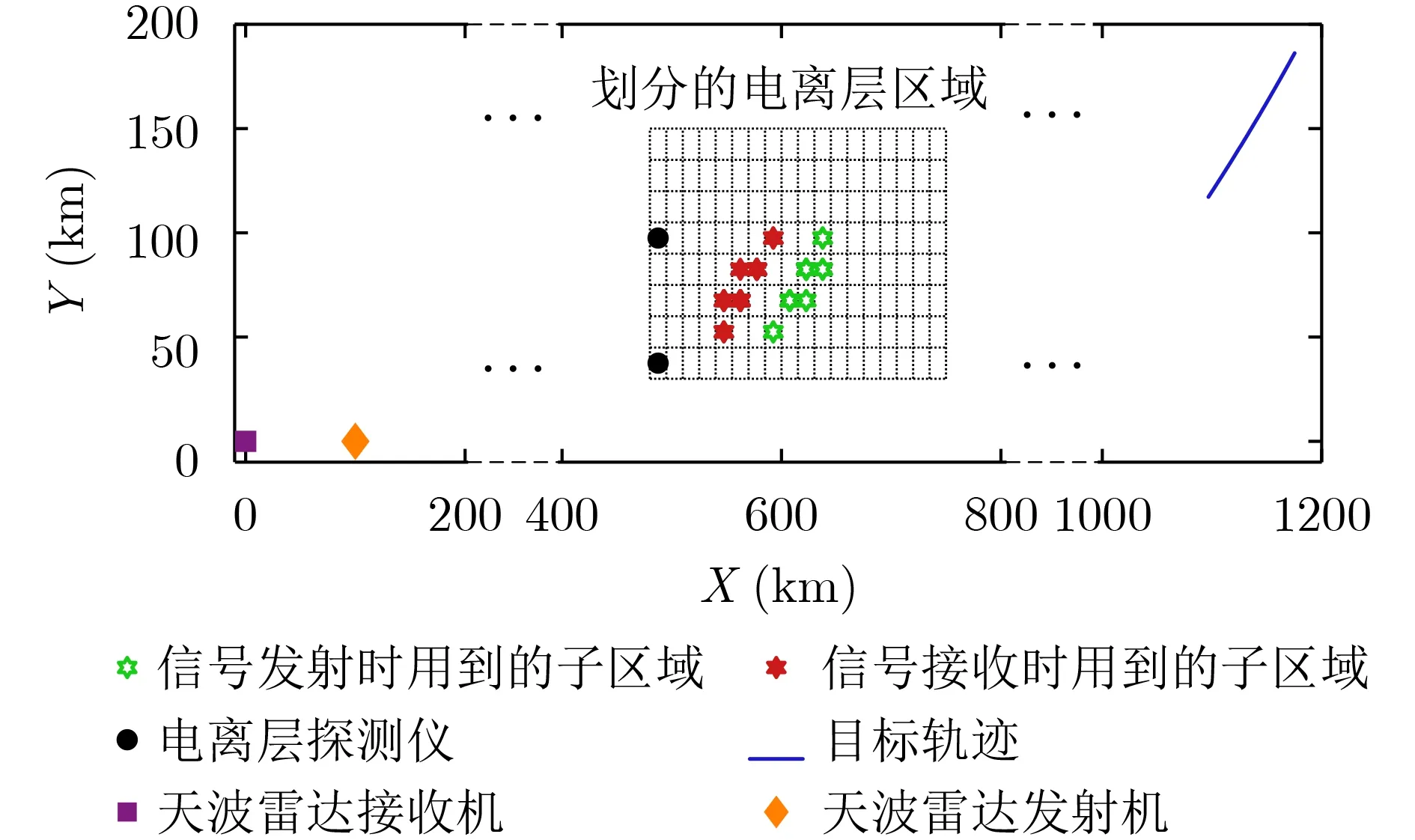
图1 仿真场景示意图
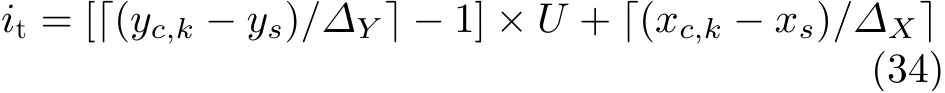


图2给出了目标使用的电离层虚高的推断结果,其中绿色点线为MPCR-GMRF使用的电离层虚高的均方根误差(Root Mean Squared Error,RMSE),该电离层虚高根据电离层探测仪实时测量和GMRF模型推断得到。红色实线为MPCR和MPDA使用的电离层虚高的RMSE,该电离层虚高为历史数据的均值。可以看出,由于利用了电离层不同位置的子区域之间的相关性和部分子区域的实时量测,MPCR-GMRF中使用的电离层虚高要比MPCR和MPDA使用的电离层虚高有更高的精度。相比于E层和F层的虚高标准差的10 km和20 km,采用了MPCR-GMRF算法推断的电离层误差分别为5.9 km和11.6 km,分别提升了41.4%和42%。

图2 目标使用的电离层虚高的推断结果
图3给出了MPCR-GMRF, MPCR和MPDA的跟踪结果的RMSE。绿色点线、橙色虚线和红色实线分别代表了新方法、MPCR和MPDA的结果。从图3可以直观地看出与MPCR和MPDA相比,新提出的MPCR-GMRF方法在径向距和方位角上精度都有所提高。相比于MPDA和MPCR在30帧中径向距平均误差分别为2.4 km和1.68 km,MPCR-GMRF的径向距平均误差降低到了1.19 km。表4给出了采用SSRSE评估的后10帧中目标跟踪相对平稳时的统计结果。从表4可以看出,在径向距、径向距速率和方位角3个方面,新提出的MPCRGMRF方法均为最优。在径向距SSRSE方面,MPCRGMRF相对于MPDA和MPCR分别减少29.4%和50.6%。以上结果表明,在提高电离层虚高推断精度的基础上,MPCR-GMRF方法达到了有效改善天波雷达目标跟踪定位的精度的目的。
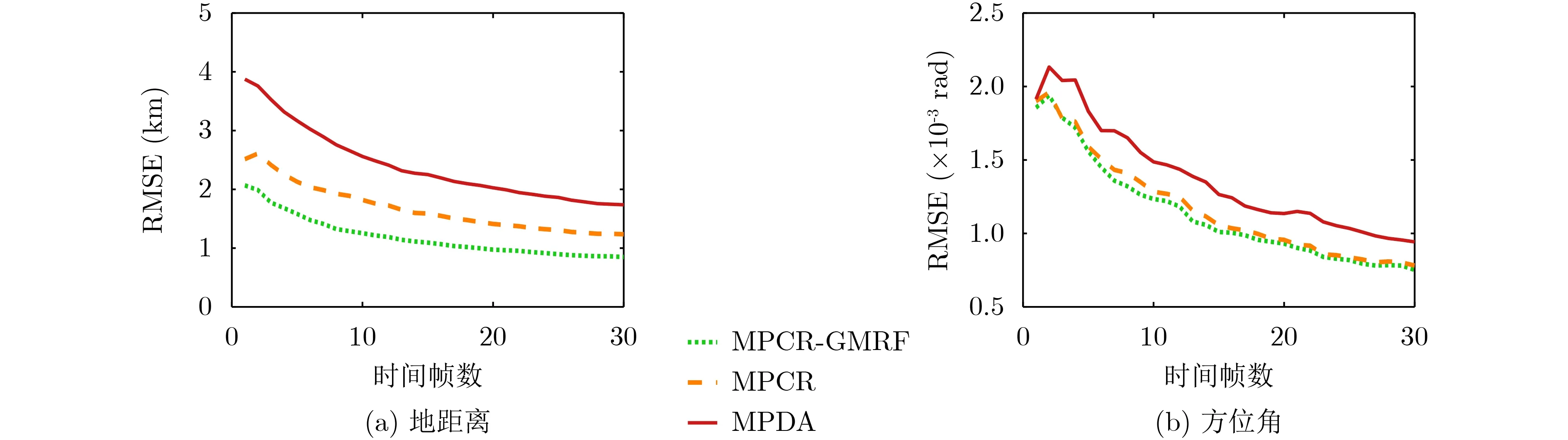
图3 目标状态估计中的RMSE
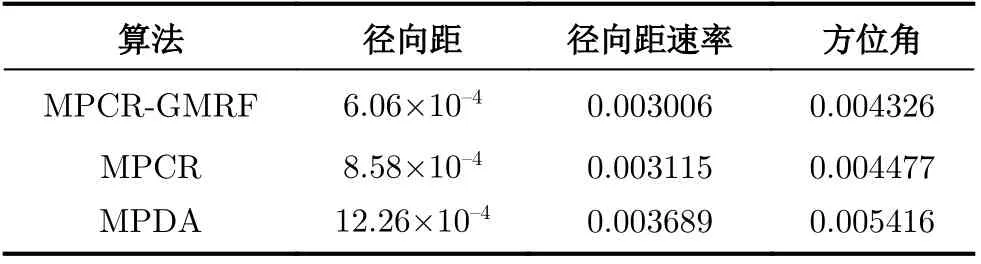
表4 MPCR-GMRF, MPCR和MPDA的SSRSE对比
5 结束语
本文在天波超视距雷达目标跟踪算法中,对电离层的现实特性,即电离层虚高随位置变化且在不同位置之间有相关性,采用GMRF进行建模,提出一种新的天波雷达目标跟踪MPCR-GMRF算法。在电离层量测由于客观因素比较有限的情况下,未量测区域的电离层虚高可以利用空间相关性推断得到,且精度比先验值高,从而达到改善天波雷达目标定位精度的目的。数值仿真对比表明有部分电离层量测且采用MPCR-GMRF推断的情况下,E层和F层虚高估计精度相对于先验值分别提升了41.4%和42%。相对于MPDA和MPCR算法中的平均目标径向距定位误差分别为2.4 km和1.68 km,MPCRGMRF将该误差降低到了1.19 km。同时,在径向距稳态相对误差方面,MPCR-GMRF算法相对于MPDA和MPCR分别减少29.4%和50.6%。数值仿真结果表明,在对电离层虚高更加贴近实际情况的建模方式下,本文新提出的MPCR-GMRF算法有效提高了天波雷达目标跟踪精度。未来的研究包括采用电离层实测数据对模型进行误差分析实验,以提供更加翔实的实测数据支持。

