软件定义网络中基于时延和负载的多控制器部署策略研究

黄梅根 袁 雪 吴令令 孙培斯

(重庆邮电大学计算机科学与技术学院 重庆 400065)

1 引言

SDN(Software Defined Network)起源于2006年斯坦福大学的Clean Slate研究课题[1]，是一种将数据转发功能与控制逻辑解耦的新型网络架构，具有集中式控制、可编程性、开放性以及灵活的网络管理等特点[2]。经典SDN网络架构依赖拥有全局视图的单一控制器，在中小型网络中，可以胜任网络的管理。但在大规模网络环境中，随着转发设备和终端的增多，单一控制器有限的资源和处理能力难以及时处理大量流请求，因此依赖单一控制器的SDN网络架构存在可扩展性问题。

为了解决这一问题，业界提出通过部署多个控制器来分担网络中的各种处理请求，以减少单个控制器的负载，从而提高整个控制平面的处理能力。对于一个给定的网络拓扑，部署多个控制器往往需要考虑3个方面：网络中需要多少个控制器、这些控制器应该放在哪里以及网络中交换机的归属问题。

Heller等人[3]首次提出控制器放置问题(Controller Placement Problem， CPP)，并将控制器位置问题作为设施位置问题来解决，试图最小化平均传播延迟和最坏情况传播延迟。他们表明，最优安置的控制器延迟明显优于随机安置的控制器，但该算法未考虑控制器负载；Zhang等人[4]以网络可靠性、控制器的负载均衡和响应时间为度量，使用自适应细菌觅食优化算法来解决控制器放置问题，但未考虑控制器时延问题；文献[5，6]都考虑在控制器负载不超过其容量的情况下，用不同的算法最小化控制器到节点的延迟或者控制器到控制器的延迟，但这些算法仅考虑了传播时延；文献[7]主要考虑控制器负载，提出一种近似比为2的多控制器负载均衡算法；文献[8，9]利用博弈论处理交换机迁移，通过重新分配交换机而不是添加或删除控制器来实现控制器的负载平衡，以达到最大化整个网络效用即最大化每个控制器的资源利用率，但并未考虑到时延问题；Wang等人[10]考虑端到端的传播时延以及控制器排队时延，提出聚簇网络划分算法来减少端到端的传播时延，并放置多控制器来减少排队时延，但未考虑控制器负载问题；文献[11]尝试使用改进的NSGA-II(非支配排序遗传算法)来解决最小化延迟和容量管理的问题，但仅考虑了传播时延；文献[12]使用修改后的ap聚类算法对网络进行分区，自动计算聚类数量并识别出最佳的控制器部署位置，但该算法仅考虑了控制器之间的传播时延；文献[13]提出多种优化模型用于控制器部署及故障处理，但仅考虑了交换机到控制器的传播时延。

综上所述，大多数研究只考虑了传播时延，然而网络中除数据包发送和传输所需的时延外，每次交换机转发都需要时间，且距离控制器的跳数越多，所需转发时间就越多。此外，控制器和交换机所需的排队时延又与网络流量有一定的关系，网络流量越大，排队时延就越大。可见每一种时延都对CPP有一定的影响，因此为了更好地部署控制器，应当综合考虑网络中可能产生的各种时延。故本文考虑总时延和控制器负载均衡，引入谱聚类，并改造该算法中的K-means算法来保证连通性的同时加入离群点处理算法和负载均衡处理算法，将网络划分成一定数量的子网域，并在每个子网域中选取合适的位置部署控制器，达到降低网络总时延和均衡控制器负载的目的。

2 SDN控制器放置模型

2.1 问题描述

SDN控制器的部署过程中，应该尽量满足以下几个条件：(1)低成本。出于对成本的考虑，在满足需求的情况下，控制器的数量应该尽量少；(2)低时延。网络时延是控制器部署中非常重要的一个性能度量，主要由传播时延、处理时延、发送时延和排队时延组成，在很大程度上影响网络的性能。为了保证网络的性能，应该使网络中的总时延不超过一个给定的阈值，并且总时延越低越好；(3)负载均衡。在SDN网络中，控制器的负载均衡也是一个不可忽略的度量。控制器的负载越大，则其对于流的处理时间会越久，从而容易造成控制器处理效率低下，影响整个网络的性能。因此，均衡各个控制器的负载，能够有效提高整个网络的服务质量。

基于上述考虑，SDN控制器部署问题可以抽象地描述为：对于任一给定的网络拓扑，已知所需子网的个数、控制器的处理速率以及交换机的流请求速率，求解该网络最佳的子网划分方法以及每个子网中最优部署控制器的位置，使整个网络的总时延尽可能小，并且每个区域内控制器的负载尽可能均衡。

2.2 系统模型

将SDN网络建模为无向图G=(V，E)，其中V表示网络中交换机和控制器节点的集合，E表示连接交换机和控制器的链路，n表示V中节点的个数。假设在SDN网络中需要放置k个控制器，则控制器的集合可表示为C={i|i=1，2，...，k}且控制器i管理的交换机集合表示为CVi。则在对SDN网络进行分区时，需要满足

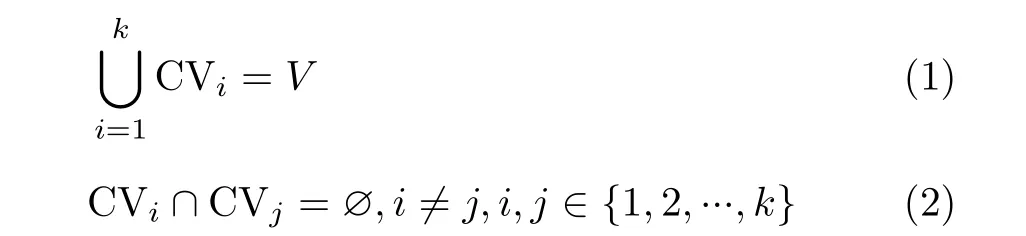
式(1)表示总子网需要覆盖所有的网络节点元素，式(2)表示每个子网中的交换机节点有且仅有1个控制器来对它进行管理。

为进一步阐述控制器放置问题，接下来将对研究部署时需考虑的度量进行定义。

定义1 端到端时延。如图1所示，从交换机1到控制器传输数据包的端到端时延主要由3个部分组成：数据包传输时延(TDi)、数据包传播时延(PDi)和交换机处理时延(SPDi)。数据包传输延迟也称发送时延，是指从开始发送数据帧到发送完毕所需要的全部时间，由TDi=PLi/BWi给出，其中PLi是链路i中数据包的长度，BWi为该链路的带宽。数据包传播时延是指数据包在链路上传播所需要的时间，可由PDi=Li/TS计算而出，Li为链路i的距离， TS为链路上介质的传播速度。另外，交换机处理时延SPDi受交换机负载的影响。因此数据包从交换机Si到控制器Cn的端到端时延可表示为

图1 SDN网络中的端到端时延

定义4 总时延。总时延分为两个部分：(1)子网总时延；(2)网络平均总时延。当网络中有新的数据包进入交换机，交换机没有对应的流表时，交换机会向对应的控制器发送Packet-in请求消息。控制器收到该消息后，对其做出相应的决策和处理后，向交换机下发所需流表。这一过程所花费的时延，可由式(8)和式(9)表示

式(12)为需要优化的目标函数，α为权重因子。式(13)为α的取值范围。式(14)表示任一控制器的负载不能超过其处理能力，即不能过载。

3 控制器部署算法

3.1 算法分析

控制器部署问题是一个带约束的多目标组合问题，因此本文考虑使用谱聚类算法来求解该问题。对于给定的网络拓扑图G=(V，E)，目标是将其切成k个互相没有联系的子图，每个子图点的集合为A1，A2， ···，Ak，其中Ai ∩Aj=Ø且A1∪A2∪...∪Ak=V。

谱聚类中使用的是标准的K-means算法，但标准K-means算法的分类目标是为了使内部的距离变小，没有考虑到类中节点的数量，这样很容易造成局部最优。除此之外，标准的K-means算法并不能直接应用于网络拓扑分区，原因如下：首先，随机选择初始中心并不能保证每个分区的质心与其关联节点之间的最大延迟；其次，标准K-means算法是基于欧氏距离将节点分配到一个集群中的，然而由于初始中心是随机选择的，所以可能不存在物理链路，因此在实际网络中使用欧氏距离并不总是可行的。

为了实现控制器的均衡部署，使用改造的Kmeans算法，实现均衡的谱聚类，在保证总时延较低的情况下，达到均衡各个控制器间的负载的目的。

3.2 MCPA算法实现

本文改造标准的K-means算法，首先用Dijkstra算法取代欧氏距离来求解出各相连节点的端到端距离，保证网络的连通性；其次，在初步完成分区之后，加入离群点检测算法，若发现孤立节点，则采取邻近法进行再分配以确保所有的交换机节点都分配到了相应的控制器；最后加入负载均衡处理，保证子网总时延较低的情况下，控制器不过载。

如表1所示，该算法分为3个阶段：(1)数据降维处理阶段(步骤(1)—步骤(8))；(2)网络划分阶段(步骤(9)—(19))；(3)子网调整阶段(步骤(20)—步骤(33))。在网络划分阶段，首先计算各个点到初始选取质心的端到端距离，然后根据距离将节点分配给相应的质心后以时延总和最小为条件找出真正的质心(步骤(16)—(19))。当初步完成分区后，进入子网调整阶段，先进行离群点检测，若存在未分配到的节点，则使用重分配算法以就近原则对该节点进行分配(步骤(24))。在保证所有节点都划分到对应的区域后，选择负载最大的子网，找出边缘区域的交换机节点作为拟移动节点(步骤(32))，以距离和F为指标不断调整拟移动交换机的分配，直至BLP-1接近一个极小的值(步骤(30)—步骤(33))，最终产生k个负载均衡的子网。

表1 基于时延和负载的多控制器部署算法

4 仿真实验

为评估本文提出的控制器部署算法，采用Internet2 OS3E网络和ChinaNet网络进行仿真实验。这两种网络广泛使用于评估控制器部署问题，也是所选取对比算法之一中基于聚类的网络划分算法(Clustering-based Network Partition Algorithm，CNPA)[10]用于验证的网络拓扑。考虑到真实网络拓扑的连通性，采用Haversine公式计算拓扑中节点之间的距离，并使用Dijkstra算法来计算节点到节点的最短路径距离。设置控制器服务速率为1 kpps，以保证一个请求可以在1 ms内处理完成，并规定每个交换机的流请求独立且最大为0.1 kpps[10]。分别与K-means、谱聚类(Spectral Clustering)和CNPA在平均总时延、最大端到端时延以及控制器负载方面进行比较。

实验1 验证在不同的网络拓扑中，MCPA，Spectral Clustering， CNPA和K-means在最大端到端时延上的差异，实验结果如图2(a)和图3(a)所示。MCPA和CNPA在端到端时延的差值并不大，说明提出的算法在最大端到端时延性能接近CNPA。而Spectral Clustering较高的原因可能是聚类的时候采用的传统的K-means算法，选取的质心并不一定是最优的，因而导致端到端时延增大。

实验2 验证在不同的网络拓扑中，MCPA，Spectral Clustering， CNPA和K-means在平均总时延上的差异，实验结果如图2(b)和图3(b)所示。随着控制器的增加，平均总时延都在下降，但K-means算法始终高于其他3种算法。分析其原因可知，Kmeans每次选择节点加入的时候，会以最小距离为条件改变控制器的位置，这一做法虽减小了传播时延，但忽略了控制器的负载情况，在大规模网络中部署少量控制器时，容易出现局部控制器负载过大，导致排队时延增加。CNPA总体高于MCPA算法和Spectral Clustering可能也是因为没有考虑控制器负载，增加了排队时延，导致总时延增大。

实验3 验证在不同的网络拓扑中，MCPA，Spectral Clustering， CNPA和K-means在控制器负载上的差异，实验结果如图2(c)和图3(c)所示。在图2(c)中，MCPA算法下的控制器负载参数始终接近1.0，且最小的时候达到了1.05，最大值为1.3，优于其他3种算法。分析原因是：K-means是以减少传播时延为目标的，未考虑到控制器的负载情况，导致控制器的负载增大。在图3(c)中，控制器数量达到5后，随着控制器的增加，CNPA的负载参数逐渐递增，分析原因可能是该算法虽改进了K-means算法，保证了连通性，但并没有考虑控制器负载。负载参数最小的是MCPA算法和Spectral Clustering，且MCPA算法更低一些。这是因为谱聚类算法虽然采用了RatioCut来划分网络，具有了一定的均衡作用，但其采用的还是传统的K-means算法进行最后的聚类，因此不及经过改造K-means后的MCPA算法。

图2 OS3E网络中的性能指标

图3 ChinaNet 网络中的性能指标

5 结束语

本文提出一种基于子网划分的多控制器部署方法。该算法改造谱聚类算法，添加离群点分配算法和负载均衡处理算法，保证了网域内各设备间的连通性，实现了时延和负载限制下控制器的均衡部署。通过在真实网络拓扑上进行仿真实验，与标准的谱聚类等算法进行对比，结果表明本文提出的控制器部署算法能够有效地对网络进行划分，使网络中控制器和交换机之间保持较小的网络总时延以及使各个控制器的负载保持均衡。未来将进一步完善MCPA，使其能够达到更好的效果。