两类非线性密码组件可重构研究与电路设计

连宜新，陈 韬，李 伟，南龙梅

（战略支援部队信息工程大学密码工程学院，郑州 450001）

0 概述

对称密码在网络和通信领域应用广泛，其按照加密方式的不同可进一步分为序列密码算法和分组密码算法［1］。在基于比特级操作［2］的序列密码算法中，非线性布尔函数成为其核心部件，在乱源更新和乱数生成过程中都参与运算，而s 盒是分组密码唯一的非线性部件，为算法提供了非线性性和安全性，两者本质上都是非线性布尔函数，但在密码芯片实际处理中却存在不同的实现方式。在s 盒实现方面，由于s 盒构造方式的不同，国内外研究分为通用和专用s 盒的实现加速，在通用领域［3-5］均采用时序部件8-8的RAM 搭建可重构运算单元，可不同程度地并行实现常规类型的s 盒，区别在于文献［5］在电路的基础上增加了旁系电路，通过门控技术降低了s 盒功耗。而文献［6］将s 盒作为非线性布尔函数，利用与或阵列的形式搭建可重构s 盒电路。在专用领域，s 盒的实现主要针对基于塔域求逆和仿射变换设计s 盒的算法，如AES、Camellia、SMS4 等。文献［7-8］根据有限域上域的扩张理论，采用组合逻辑的方式优化单算法AESs 盒。文献［9］提出的复合域求逆运算模型针对有限域求逆的s 盒，其本质上仍然是域的扩张理论，文献［10］将AES、Camellia、SMS4 等s 盒电路采用GF（16）上的运算搭建进而重构，其核心的求逆电路相同，区别只是在于求逆电路输入前和输出后的转换矩阵。在针对序列密码的非线性布尔函数（NBF）实现方面，单算法设计如文献［11］采取直接实现的方法，而面向密码处理的NBF 设计结构具有通用性，其可重构设计借鉴了FPGA 思想。文献［12-14］在统计序列密码NBF 运算特征，即参与运算变量个数与项次数基础上采用LUT 搭建实现，其结构的区别在于LUT 选取的粒度和规模不同。

但以上设计均只是从某种或者某类算法的角度出发，并未将对称密码非线性运算模块统一，实际上两者本质上并无区别，这样的异构化设计必然存在资源浪费的问题。此外由于s 盒一般采用并行化处理，这使得s 盒成为密码处理器中资源消耗最大的模块，如何降低对称密码非线性运算面积开销是急需解决的问题，因此可以采取一种统一的结构实现以降低硬件开销。

本文设计一种s 盒非线性布尔函数模块（Sbox_Non-linear Boolean Function Module，SNBFM）架构，在MBFM 架构的基础上融合部分类型的s 盒，并结合有限域理论，对其中能够优化的类AESs 盒进行适配，使其对类AES 的s 盒支持力度更高。

1 可重构分析

1.1 两类非线性密码组件操作特征分析

在对称密码中，s 盒和非线性布尔函数都是作为异构的模块单独实现，其中NBF 在序列密码的编码环节［15］，即乱源更新，在乱数生成的过程中均参与运算，其通用表达式包含1，2，…，n次常数项，公式如下所示：

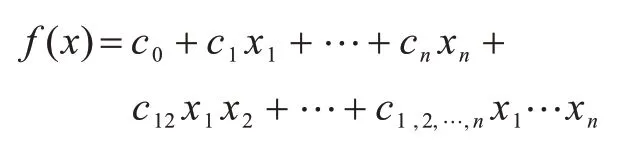
通过统计NESSIE 计划、CRYPTREC 计划和ESTREAM 计划，征集序列密码算法NBF 操作特征，即对其状态序列长度、参与运算变量个数、项个数和次数进行分析，如表1 所示，发现虽然位宽为12～256 bit，参与运算的变量个数可能很多，约为12～128 个，但与项次数多数不超过6 次，因此相应的NBF 结构均是能实现最高次数为6 的变量结构［12-14］。

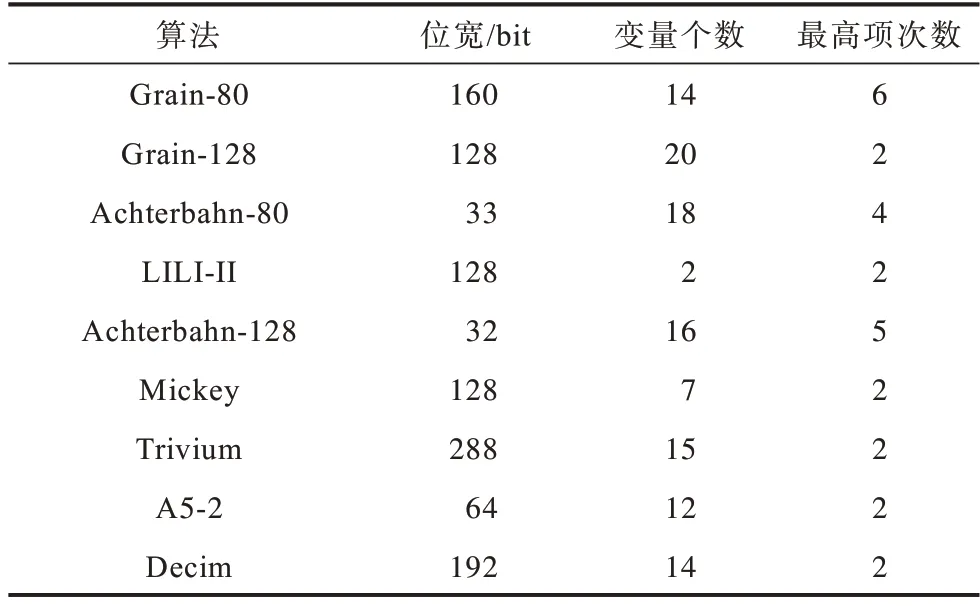
表1 NBF 操作特征Table 1 NBF operational characteristics

s 盒设计方法主要包括随机选取测试和利用数学方法产生2 种［16］，并且需要满足一定的设计准则，而硬件设计人员在s 盒实现上关注的是s 盒的操作特征，即输入和输出变量数。本文对AES 计划、NESSIE 计划以及其他商用分组密码算法的s 盒进行特征分析，发现s 盒的种类大多集中在4-4、6-4、8-4、8-8、8-32 上，同时s 盒具有一定的并行性。

1.2 NBFM 结构实现能力分析

在文献［13］所列出的4 种NBFM 结构中，其中的一种共享2 输入NBFM 结构如图1 所示，NBFM 是一个10 入4 出的结构，这类含共享变量的结构充分考虑了NBFM 操作特征，减少了端口数目，易于在处理器中集成，整体结构可以分为LUT 存储和NBFM组合逻辑两部分。适配8-8 s 盒的NBFM 如图2 所示。NBFM 实现能力如表2 所示，其中输出端用0、1、2、3 代替。将s 盒映射到NBFM 是将s 盒输出的每一路都看作输入的非线性布尔函数，然后根据输入变量的多少确定NBFM 变量模式，可以看到，NBFM对于4 输入、5 输入、6 输入的s 盒能够分别支持4 路、2 路和1 路输出，较好地支持了4-4、6-4 类型的s 盒。但由于NBFM 缺少8 变量模式，因此只能通过级联实现8 变量NBFM，图2 所示为8-8 s 盒输出任意一路在NBFM 中的适配，而各类s 盒在NBFM 中适配资源消耗如表3 所示。

表2 NBFM 实现能力Table 2 NBFM Realization ability

表3 不同类型s 盒资源消耗Table 3 Resource consumption of different types of s box

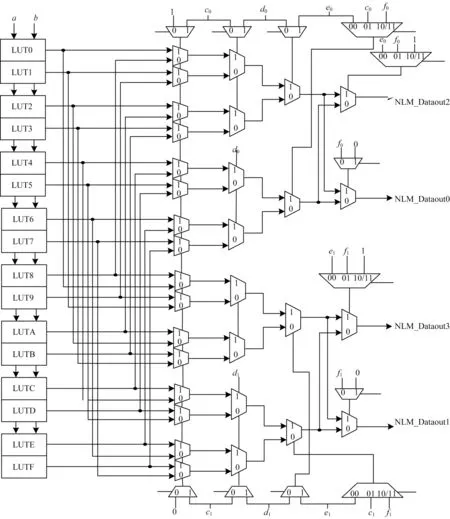
图1 NBFM 结构Fig.1 NBFM structure

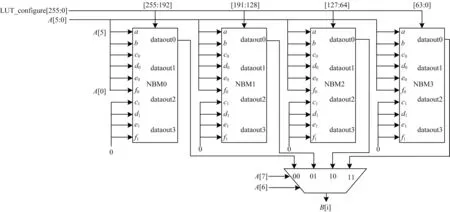
图2 适配8-8 s 盒的NBFMFig.2 NBFM of adaptation 8-8 s box

从表3 可以看出，NBFM 在实现4-4 和6-4 的s 盒上消耗资源较少，而在实现8 输入变量的s 盒上时需要多个NBFM 级联才能实现1 路输出。NBFM 实现一个8-8 的s 盒与8-8 的RAM 如表4 所示。可以看出，NBFM 在实现8-8 s 盒上效率很低，性能指标也并不如RAM 实现，但通过对8-8 的s 盒进行进一步细分发现，8-8 的s 盒中存在求逆和仿射变换构造的类AESs 盒，这类s 盒可通过组合逻辑的方法化简输出的NBF 表达式，从而易于NBFM 适配。

表4 8-8 的s 盒适配资源评估Table 4 8-8 s box adaptation resource evaluation

2 类AESs 盒和非线性布尔函数可重构研究

2.1 类AESs 盒可降解理论分析

在对文献［7-8］进行分析后发现，类AES 的s 盒存在2 种分解形式：GF（42）2和GF（（22）2）2。2 种分解形式区别在于基本模块规模的不同，而适合NBFM这种2 输入LUT 类型实现的是GF（（22）2）2，因此本文将根据混合基方法［17］推导s 盒分解后的不同模块表达式。

文献［17］采用混合基实现AESs 盒的塔域分解，具体采用的基和不可约多项式如表5 所示，其中，α是e(x)=0 的一个根，β是f(x)=0 的一个根，γ是g(x)=0 的一个根。为方便计算，记λ=α2β。塔域分解后的AESs 盒电路如图3 所示，可以看到s 盒的求逆部分由乘和求逆等5 类模块组成，δ、Aδ-1+C是复合仿射变换后的同构映射矩阵，规模为8 行8 列，负责对求逆的输入和输出进行转换。与文献［17］s 盒采用GF（16）上的模块用GF（4）模块组合实现、GF（4）上模块再用GF（2）上的运算组合实现的两级模块化设计方法不同，由于各个模块具体适配到NBFM 上时，适配的对象LUT_n表示一个n输入的NBF，最终的适配对象应该是一个个的NBF，因此只能推导出各个模块的NBF 表达式，而文献［17］的两级模块搭建方法无法深入比特级表达式，因此无法适配各个模块。下文将依次推导出求逆所包含的5 个模块的布尔表达式。

表5 不可约多项式和基的选取Table 5 Selection of irreducible polynomials and bases

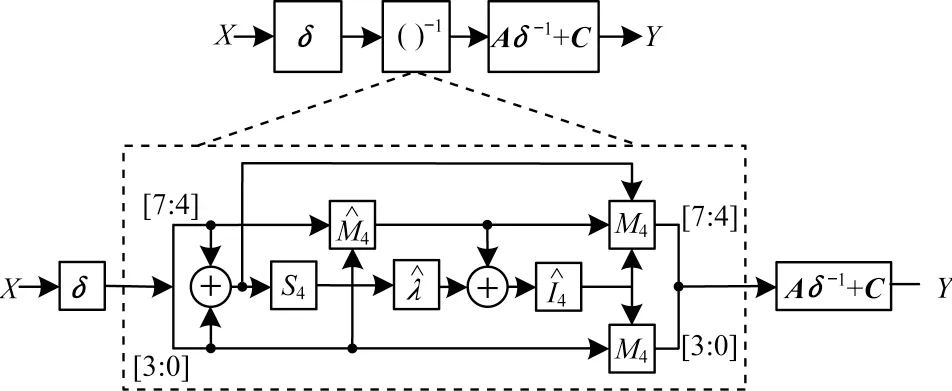
图3 塔域分解后的AES s 盒电路Fig.3 AES s box circuit after tower domain decomposition

s 盒的求逆部分包含平方S4、乘法M4、乘法常数乘法乘、求逆等5 类模块，涉及到的运算均在GF（16）上，其中S4、M4以多项式基输入和输出，乘和以多项式基输入、正规基输出。设GF（16）上元素A、B用多项式基表示：A=a0⊕a1β，B=b0⊕b1β，a0b0是低2 位，a1b1是高2 位，a0b0a1b1∈(0，1，2，3)。

S4、M4乘和求逆结果用A2、AB、AB_ptn、λA、A-1表示，则可得式（1）～式（5）。由于最后要推导出各个模块的布尔表达式，而a0b0a1b1是GF（4）并非GF（2）上元素，因此需要继续分解。可以看到，式（1）～式（5）用到的基本运算包含GF（4）上的平方S2、两类常数乘法α乘和α2乘、乘 法M2和求逆I2等4 类。GF（4）上元素用正规基表示可以简化求逆和平方的计算，设C=c0⊕c1α，D=d0⊕d1α，其中，c0d0是低位，c1d1是高位，c0d0c1d1∈(0，1)。

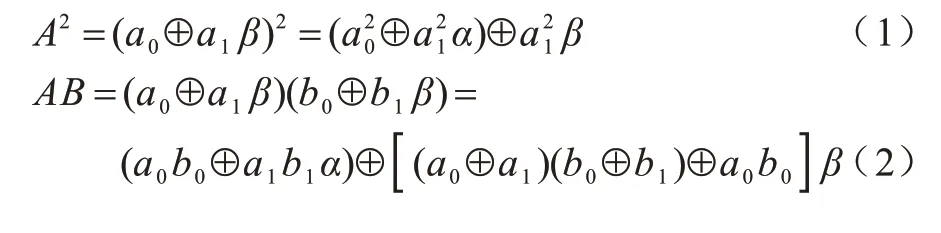
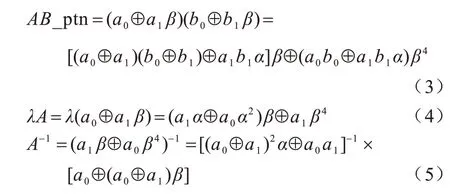
S2、α乘和α2乘、M2、I2结果分别用C2、αC、α2C、CD、C-1表示，可得式（6）～式（10）。设GF（16）上元素AB的比特形式为A={A3，A2，A1，A0}，B={B3，B2，B1，B0}，将式（6）和式（7）代入式（1）得S4，将式（7）和式（8）代入式（2）得乘，将式（6）、式（7）、式（9）和式（10）代入式（3）得，将式（7）和式（9）代入式（4）和式（5）得和M4，结果分别如式（11）～式（15）所示：

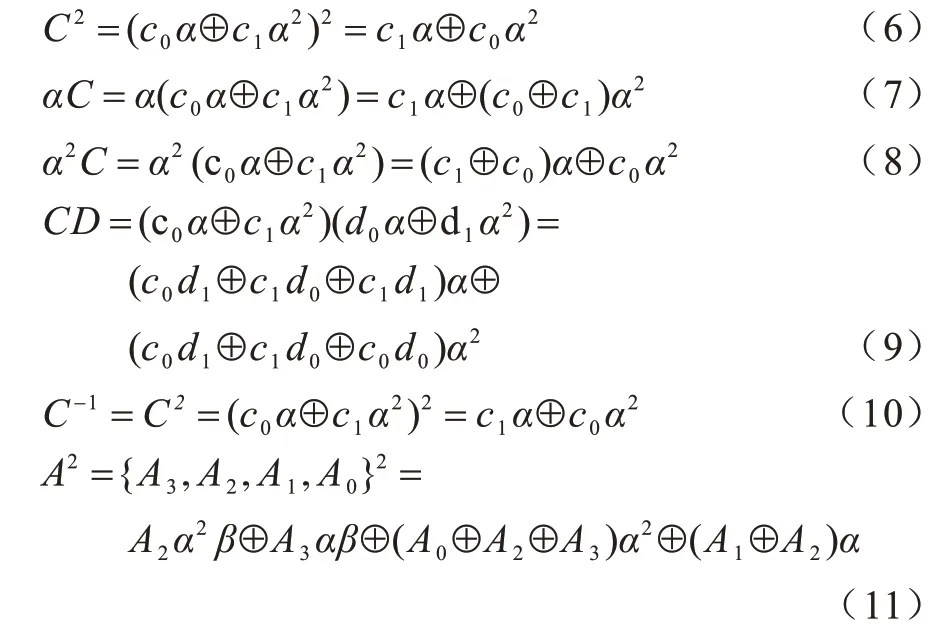
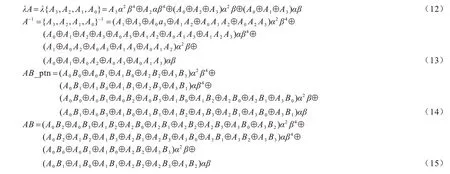
将AESs 盒求逆表达式推导完成后，由于涉及到的是类AESs 盒，因此还需要从原理上证明此类s 盒适合重构。文献［10］对AES、Camellia、SMS4等类AESs 盒做了可重构电路，其求逆统一在塔域GF（42）2上实现，区别仅在复合了仿射变换后的前后同构映射矩阵上，但并未说明其理论基础。文献［18］根据包含相同个数元素的域是同构的原理，证明了GF（256）上s 盒S和基于有限域扩张理论求出来的逆s 盒T存在线性变换A1、B1，使得S=B1（T（A（x）），并进一步证明有2 040 个这样的转换对使得s 盒原域和塔域的乘法逆s 盒保持线性变换。A1、B1即为转换矩阵，在采用统一基类型和不可约多项式的前提下类AESs 盒乘法逆T相同，这样即从原理上证明了此类s 盒存在统一的结构，为可重构电路设计奠定了理论基础。

2.2 类AESs 盒与NBFM 可重构分析

将塔域分解后的s 盒和NBFM 结构重构，即将s盒适配到NBFM 结构中，将s 盒分解到GF（16）上的各个运算，考虑各模块输入输出情况，如乘法M4是8 入4 出的结构，采用NBFM 的6 输入模式后，需要消耗16 个NBFM，具体各模块资源消耗如表6 所示，其中，异或包括求逆的2 个GF（16）上运算以及2 个转换矩阵，1 个异或门面积≈个2_LUT。

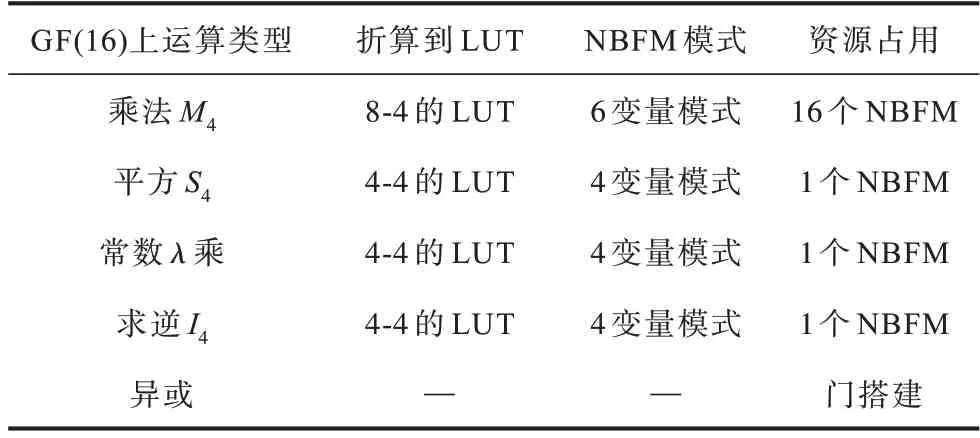
表6 各模块资源消耗Table 6 Resource consumption of each module

Sbox_area=3M4+S4+I4+λ+异或，相当于用51 个NBFM 加一部分异或门实现一个可分解的8-8 s 盒，这样效率不如直接实现，由于M4布尔表达式是8 入4 出的结构，如果直接采取NBFM 的6 变量模式搭建一个完备的NBF将导致资源浪费，冗余度过高，应该针对M4继续分解。

将GF（16）上的乘法继续分解到GF（4）上，用到3个M2乘法、1 个α 乘以及部分异或门资源，电路如图4 所示。涉及到的各模块资源损耗如表7 所示，其中，M2电路只考虑LUT 资源的情况下消耗4 个2 输入LUT，相当于1/4 个NBFM。

表7 M4资源消耗Table 7 M4 resource consumption

图4 M4电路Fig.4 M4 circuit

最后相当于 用1 个NBFM 实现GF（16）上的乘法。最终的s 盒占用变为6 个NBFM 加一部分的异或门，相比将s 盒输出展开写成NBF 表达式的方法节约了近9 倍的NBFM 资源。

2.3 结合类AESs 盒的NBFM 结构优化分析

由2.1 节对塔域分解后的不同模块表达式的推导可知，式（11）～式（15）复杂程度不一，映射到NBFM 上还是采用门级电路实现未定，根据推导出的表达式复杂程度，结合表达式输入输出特征，将各个模块分为3 类实现形式：1）基于异或实现平方S4乘和前后的同构映射；2）基于NBFM 实现求逆3）基于改进后的SNBFM 实现和M4乘法。图5 所示为类AESs 盒适配的电路，可以看到只需用到4 个NBFM 便可以实现一个完整的类AESs 盒。

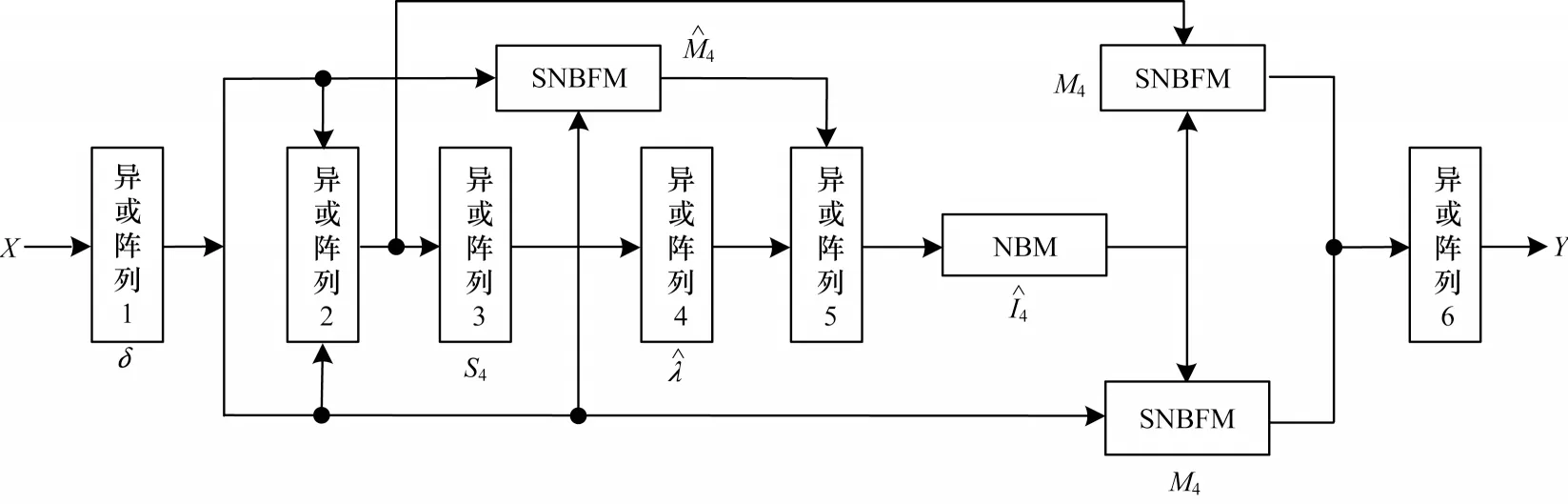
图5 s 盒适配后的整体结构Fig.5 Overall structure of s-box after adaptation

基本模块平方S4乘根据式（11）、式（12）结果只有少数的1 次项，如果采用能实现从1 次项到4 次项且变量任意组合的NBFM 的4 变量模式，将造成极大的资源浪费，考虑到s 盒实现的并行性，用较少的NBFM实现是需要考虑的性能指标，基于此，平方S4和求逆采用异或实现，这样只需要用到6 个2 输入异或门便可实现S4模块，需要7个2输入异或门便可实现乘模块。此外，同构映射矩阵也采用异或门实现，异或门的数量=矩阵中1 的数量减1，由于前后的同构映射矩阵不属于求逆部分，类AESs 盒的差别即在于此，因此设置成可配置类型，共需要128 bit 配置信息和126 个异或门，配置信息为1 时输入位取反，为0 时输入位不变。下面给出AESs盒输入转换y=和输出转换y=的转换矩阵，其中x、y均按小端排列。

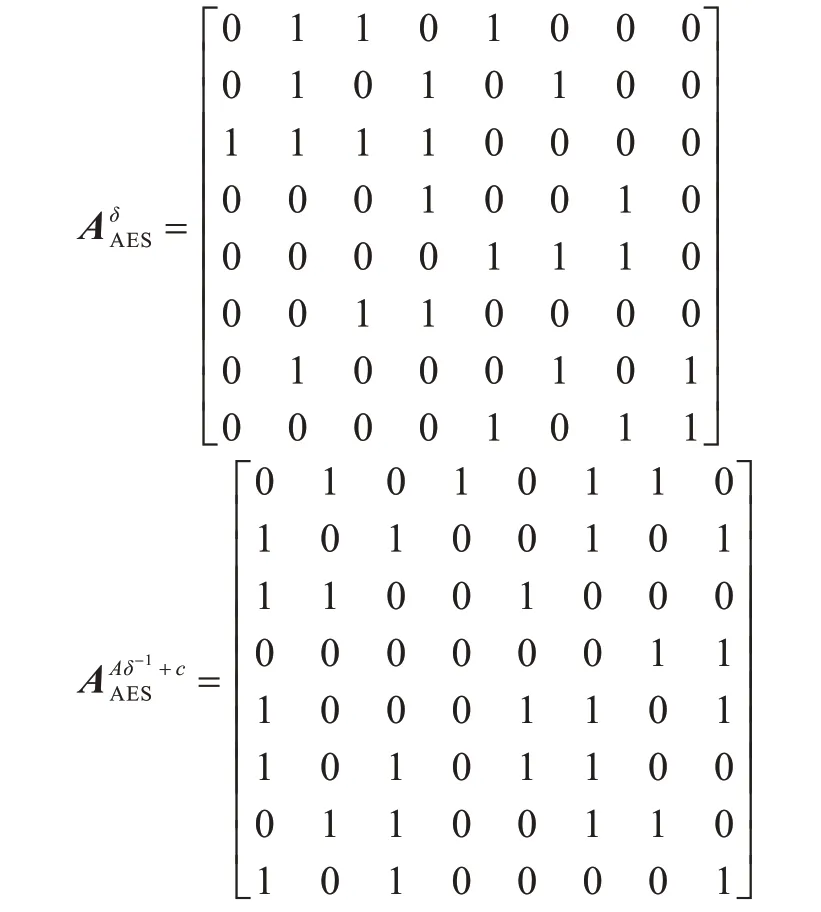
表8 电路端口映射Table 8 circuit port mapping

表8 电路端口映射Table 8 circuit port mapping

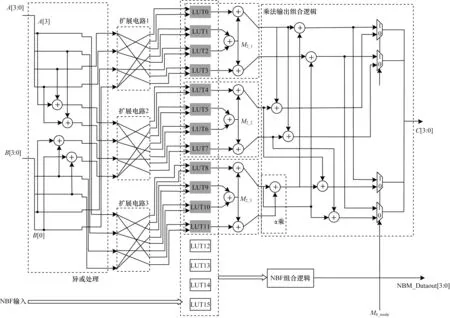
图6 SNBFM 结构Fig.6 SNBFM structure

3 性能评估

在保证NBFM 原有NBF 功能前提下，采用verilog实现各个改进的NBFM 模块，最后按照类AESs 盒电路的组织形式对改进后的NBFM进行级联实现s盒功能。功能验证通过后在CMOS 65 nm 工艺库下对该电路进行综合，与塔域直接实现的s 盒电路和NBFM 电路进行对比分析后的结果如表9 所示。

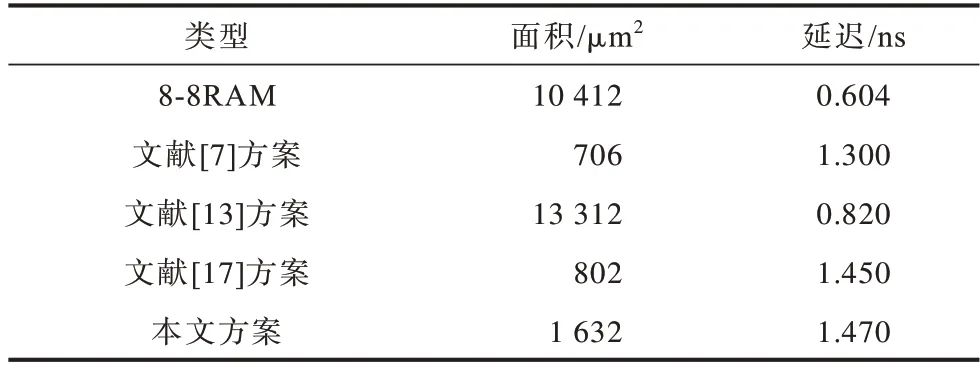
表9 电路性能指标Table 9 Circuit performance index

RAM 是一个时序部件，虽然延迟最小但规模过大，而文献［13］的NBFM 结构在适配s 盒时将s 盒作为NBF 适配，这种方法虽然适合通用8-8 的s 盒，但由于NBM 最多只能支持6 变量模式，因此NBFM 个数消耗过多以致占用资源最多。这种NBF 适配的方法适合6 变量、4 变量输入的s 盒，但并不适合8-8 的通用s 盒。文献［17］所选用的塔域分解是一种用组合逻辑的方法实现AESs 盒，其目的是为了降低面积开销，但是这种组合逻辑的方法在单个算法s 盒性能表现上并不是最优的。文献［19］将各模块的表达式推导出以后，采用CSE 算法将其中的各模块表达式含有的公共项消除进一步减少了s 盒面积和延迟。本文验证了类AESs 盒电路差异仅在转换矩阵上，实现了类AESs 盒和NBF 的可重构，由于可重构的结构是要实现两类非线性运算，但NBFM 的结构并不适合对类AESs 盒直接实现，需要对NBFM 进行改进，这使得NBFM 的电路资源并非完全参与s 盒的运算，采用CSE 算法也会造成一定的冗余度。也因此，本文采用类似的塔域分解的方法，相比文献［19］增加了1 倍多面积。

但实际上面积不是唯一的指标，由于牵扯到复杂的NBF 适配，NBFM 的个数是多个级联在一起，因此在保证充分复用前提下用最少的NBFM 个数来实现s 盒。本文采用的方法相当于在4 个改进后的NBM 电路加一部分异或阵列，可以看到在4 个NBFM 基础上增加1 632-362×4=184 μm2实现了一个类AES 的8-8 的s 盒，相当于只用22.7%的s 盒电路面积实现了一个类AES 的s 盒，而电路延迟基本不变。

在电路实现功能上，如表10 所示，由于塔域分解定理只针对部分s 盒，因此并不能实现通用的8-8 s 盒的实现。

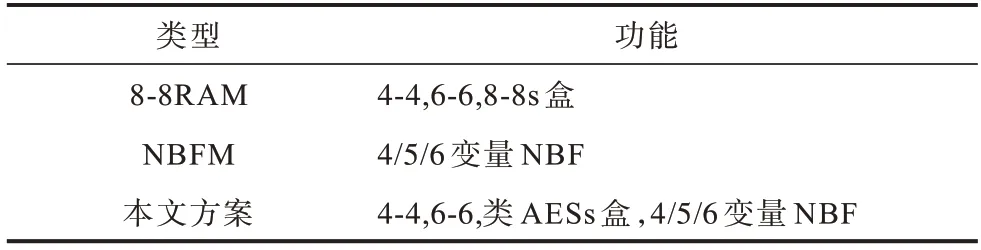
表10 电路实现功能的对比Table 10 Comparison of circuit realization functions

4 结束语

本文实现了类AESs 盒和NBFM 的可重构电路，并基于塔域分解理论，提出一种新的SNBFM 结构。采用混合基方法将AES 类s 盒电路分解为GF（16）上的各种运算模块，并推导出这些模块的位级表达式。实验结果表明，改进后的整体结构只用到4 个NBFM加上原s 盒的22.7%面积实现一个完整的类AESs盒，而延迟基本不变，并保证了已有NBF 功能。但类AESs 盒相比通用s 盒种类较少，使得该结构的用途受到限制，下一步将研究运用更少的资源实现通用s盒和NBF 的可重构，并通过扩展指令的方式加速密码运算［20］。