基于相似性多色谱图像融合的降噪技术*

张亚婉，钟其麟，陈威宇

（广东工业大学华立学院，广州 511320）

0 引言

随着计算机技术的快速发展，图像处理技术在医学成像、人脸识别、地质勘察等方面得到了广泛的应用，人们对图像处理的精度要求越来越高[1]。图像的采集、转换与传输等过程中，常常受到光照、天气和成像设备等外界条件的影响以及电磁波和元器件等内部条件的影响，会出现一些离散、孤立的图像噪声点，可采取图像融合技术降低图像噪声，提升图像质量[2]。图像融合是根据多尺度几何变换、多种数学模型和数学理论，利用图像处理技术将多幅具有互补特性的图像进行融合，形成分辨率高、信息量大而准确的图像。遥感图像融合领域中普遍使用多尺度分析算法、成分替代算法、混合算法以及基于模型的算法等[3-4]。基于多尺度分析的经典算法有有离散小波变换、拉普拉斯金字塔变换等[5]。

传统的拉普拉斯金字塔分解的冗余数据具有关联性，分解方向固定，导致算法难以提取图像的细节结构信息，随着分解层的逐步增加，分辨率越来越小，导致图像边界噪点变多[6]。本文提出一种改进的拉普拉斯金字塔变换的相似性多色谱图像融合技术，通过拉普拉斯金字塔对源图像进行预处理和分解，得到一系列高分辨率的细节系数和一系列低分辨率的近似系数。在低分辨率的融合子图像上运用自适应分割算法，以区域为单位提取图像特征，然后比较区域内的SML 值，获得近似系数融合的初始决策图。再使用引导滤波算法对初始决策图进行优化，通过最终决策图像素值加权方法将近似系数进行融合[7]。在细节系数上采用Canny算子对图像进行边缘检测处理，并依据最终决策图对高水平细节系数采用局部区域梯度能力取大方法实现融合。根据源图像的像素值逆变换原理得到的近似系数和细节系数重构得到一幅融合图像[8]。

1 自适应差分进化算法

差分进化算法是一种多目标优化算法，目前已经成为一种求解非线性、不可微、多极值和高维复杂函数的一种极其有效的方法[9]。主要有变异因子F和交叉因子cr两个参数，如下式所示：

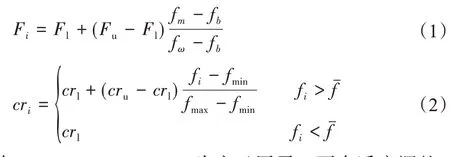
式中：Fl=0.1；Fu=0.9；cr为交叉因子，可自适应调整，cr=[0,1]；fmax和fmin分别为当前种群中最优和最差个体适应度；为其平均值；crl下限值取0.1，cru上限值取0.6。

自适应差分化算法在不同阶段F和cr的值，可以收敛为一个合适的解，并以较小的图像质量的代价来保证算法效率。

2 拉普拉斯金字塔融合（LP）

2.1 传统的拉普拉斯金字塔变换

利用传统的拉普拉斯金字塔图像融合方法，其过程主要分为两步，首先将源图像分解为高低频率系数，使用不同的融合策略完成对不同的系数的各层次各方向的融合，最后通过反变换得到融合后的图像[10]。其中IX、IY为输入源图像，LX、LY为不同源图像分解后的低频系数，HX、HY为高频系数，IF为融合后的效果图。如图1所示。

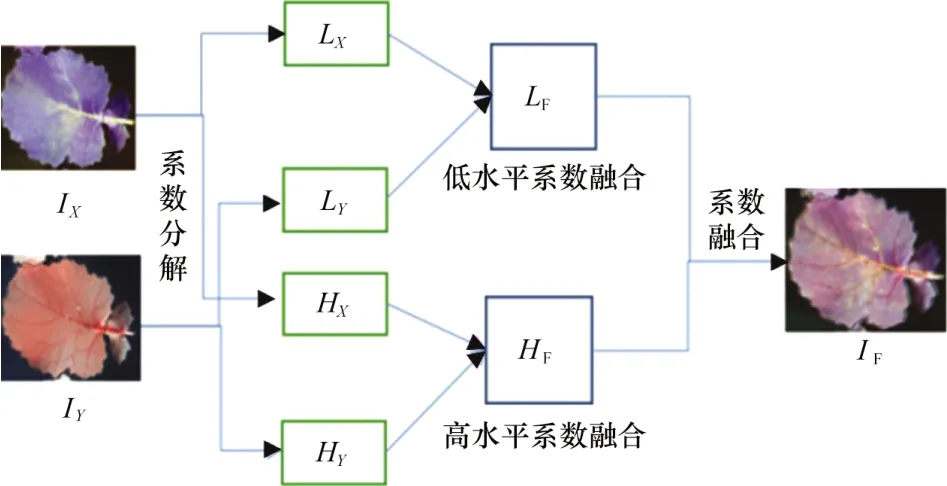
图1 传统变换域图像融合过程

传统的拉普拉斯金字塔变换的融合效果一般，分解后的数据总量比源图像多出1 倍，而且难以提取图像的细节结构信息[11]。

2.2 改进的拉普拉斯金字塔变换

根据拉普拉斯金字塔对源图像进行预处理和分解，获得一系列高分辨率的细节系数和一系列低分辨率的近似系数。在低分辨率的融合子图像上运用自适应分割算法以区域为单位提取图像特征，当源图像大小为M×N，建立初始决策图大小为M×N的全零矩阵DP（x，y），用于保存聚焦结果。通过区域化改进确定拉普拉斯能量和多聚焦度的度量。对于SA（x，y）和SB（x，y），利用比较的方法获取初始决策图如下：

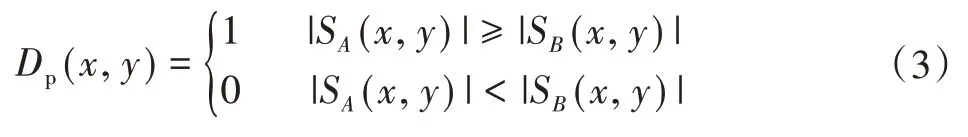
从图2（a）中可以看出，初始决策图存在较多小黑块，可使用众数滤波算法优化初始决策图，以块为处理单位，将具有近似值足够多并且在滤波器内核周围必须是连续的相邻像元数进行替换以完成小孔洞的填充，效果图如图2（b）所示[12]。

图2 初始决策图效果

因采用聚焦程度测量功能获得近似系数会导致初始融合效果不理想，边界处不平滑，故引入图像引导滤波算法进行优化。根据图像结构一致性原理，将源图像的结构信息复制到决策图上[13]。为提高精度可适当降低分解层数。通常情况下取r=8，本实验中，将分解层降低到1～5层，滑动窗口半径以8为基准，对不同的分解层应用不同的滑窗半径，r=8-level，level 为分解层[14]。效果图如图3所示。

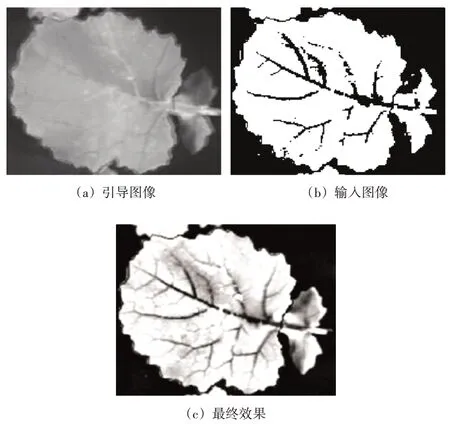
图3 最终决策图效果

采用Canny 算子在细节系数的融合子图像上进行图像边缘检测，通过计算得到梯度幅值G（x，y），再选取合适的阈值τ，若G（x，y）＞τ，则（i，j）是边缘点，反之，（i，j）为非边缘点。用以上方法得到二值图像{g（i，j）}[15]。其梯度模和方向如下式所示：

用fs=f(x,y)·G(x,y)进行平滑运算，利用一阶微分算子计算边界点的位置。平滑后的梯度参数可用下式近似：

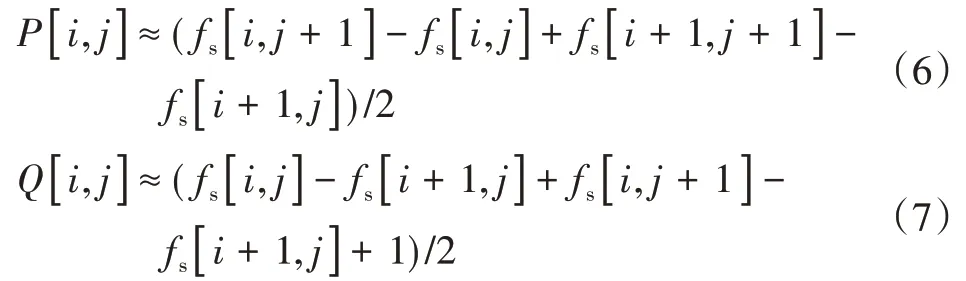
幅值M[i,j]和方向角θ[i,j]可根据下式进行计算：

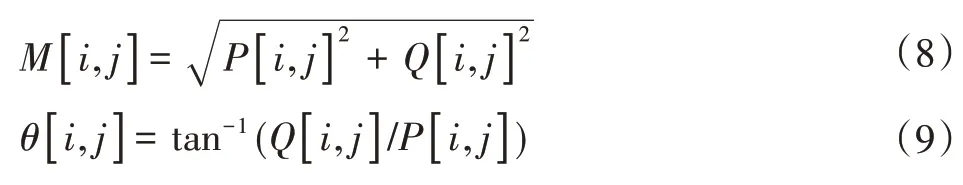
幅值M[i,j]表示图像边缘强度，θ[i,j]表示边缘方向，利用Canny算子进行图像边缘检测，抑制了噪声引起的伪边缘，使边缘细化。即使对于对比度较低的图像，可通过调节参数方法，进行检测，其检测结果如图4（b）所示。

图4 检测图像

输入系数LA（x，y）和LB（x，y）、LF（x，y）为近似系数融合后的系数，Df（x，y）为权值，根据加权融合的规则实现融合，如下所示：

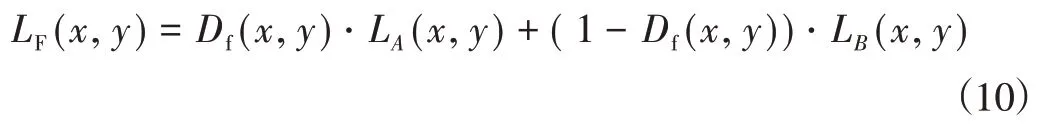
细节系数能表示图像的全部细节信息，局部能量取大法是常用的处理方法。一个坐标为（i,j），大小为m×n的窗口Q的局部能量的定义如下所示:

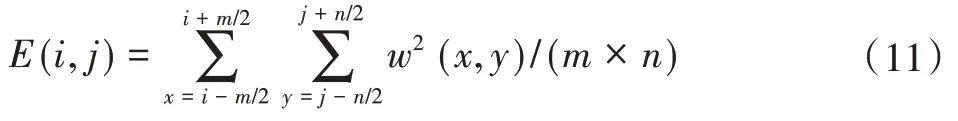
其中，当前窗口的具体坐标为金字塔细节系数为w（x，y），（x，y）∈Ω。细节系数在不同层次尺寸有所不同，实现分块如果采用固定大小会影响最终结果。近似系数根据差分进化理论获取了自适应的决策图Df（x，y），结合Df（x，y）对细节系数进行决策判别，对细节层数实现逐层融合。系数融合如下所示：

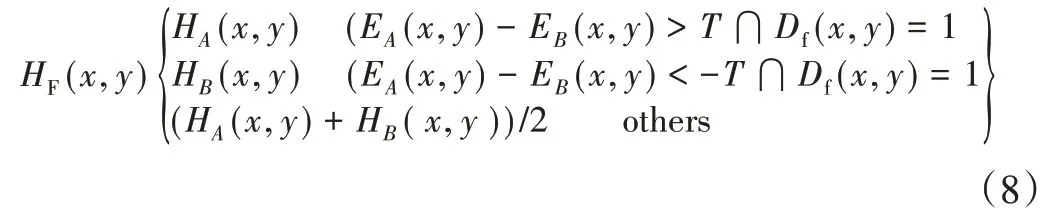
式中：HA（x，y）和HB（x，y）为两幅细节融合系数（x，y）处的值；Df（x，y）为自适应决策图上（x，y）处的取值；T为阈值，取值范围为[0,1]之间的常数[16]。

3 实验仿真与分析

利用MATLAB 软件，通过利用对改进后的算法进行图像融合处理，根据实验设置3 种融合检测指标，分别对3种方法进行比较，图5所示为传统拉普拉斯金字塔的算法效果图，图6所示为低通比率金字塔变换的效果图，图7所示为本文研究方法的效果图。由图可知，对于3种算法进行分析，本文算法得到的图像融合效果更好，图像更加清晰，信息量更大，信息聚合度更强。

图5 传统拉普拉斯金字塔算法

图6 低通比率金字塔变换算法

图7 本文算法

为了评价融合方法的性能，选用4 种常用的融合指标对其进行评价，分别是QXY/F—基于边缘信息的评价指标，QMI—互信息评价指标等指标进行评价，各融合降噪算法的客观评价如表1所示。

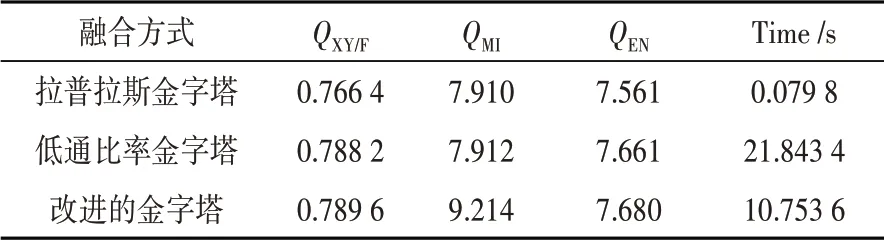
表1 各融合降噪算法的客观评价结果

本文采用了与图像本身相关联的自适应分块技术，克服了块效应，提升了特征提取的精准程度，通过MATLAB 进行仿真比较，结果表明基于此图像融合技术的降噪方法优于传统和低通比率金字塔方法。

4 结束语

为了进一步高效准确提升图像的特征提取能力，本文设计了自适应差分进化算法，通过调整缩放因子和交叉因子，实现了分割的自适应从而大大提升了图像的特征提取能力。结合拉普拉斯金字塔变换，将多源图像分解成近似系数和细节系数，利用自适应差分化算法划分区域并结合SML 值形成融合决策图，在近似系数上采取像素加权融合规则完成近似系数融合。在细节系数上采取局部区域块梯度能力取大法与最优决策图融合，融合后的近似系数和细节系数通过源图像的像素值逆变换重构。从实验仿真结果可以看出，用本文方法进行融合降噪方法的图像聚合度更强，更加清晰，并提高了图像的识别率和清晰度。从各融合降噪算法的客观评价结果看来也优于其他方法。