直流电场作用下湿型粘土砂导电特性及其应用研究
张容鹏,李大勇,石德全,马旭梁
(哈尔滨理工大学 材料科学与化学工程学院,黑龙江哈尔滨 150040)
0 引言
湿型粘土砂组分和性能参数的检测与控制一直是铸造生产的重要课题之一。因为水分和粘土是影响型砂质量的主要成分,并且水分具有独特的介电常数。因此,利用湿型粘土砂导电特性表征其含水量的研究由来已久[1]。此前有关型砂导电特性的研究主要分为直流导电特性和交流导电特性或交直流导电特性综合利用的研究。最初人们利用直流电源激励砂样检测型砂含水量,发现砂样电阻在直流电场作用下不断变化,因而无法获得稳定电阻值,导致这种最为简单的测试方法难以用于实际生产,后续研究发现引起砂样直流电阻不断变化的原因是电场作用下的介质极化[2]。研究型砂交流导电特性研究的目的在于克服介质极化的影响,以便获得稳定的砂样电阻值,进而求得型砂含水量。但是该方法对交流激励源频率和波形要求比较严格,否则难以获得理性检测结果。对砂样分别实施交直流电源二次激励,利用砂样交直流导电特性求解型砂含水量及有效粘土含量的研究是深入研究和应用型砂导电特性的有益探索。为了进一步简化测试方法,本文提出再次深入研究湿型粘土砂直流导电特性,尝试利用单一直流电场作用下型砂极化行为的特殊信息表征型砂含水量及有效粘土含量,以期获得直流电阻法在湿型粘土砂质量测控中的实际应用。
1 湿型粘土砂直流导电特性
1.1 湿性粘土砂直流导电特性检测方法
为探寻型砂直流导电特性与型砂含水量和有效粘土含量之间的关系,本文构建如图1 所示的检测装置。装置测量回路由型砂试样、恒流源和取样电阻构成,恒流源对型砂试样施加外部直流电场激励。数据采集系统由计算机和亚当模块构成,亚当模块负责实时检测取样电阻上的电压变化,计算机负责处理信息参数。取样电阻与型砂试样串联。
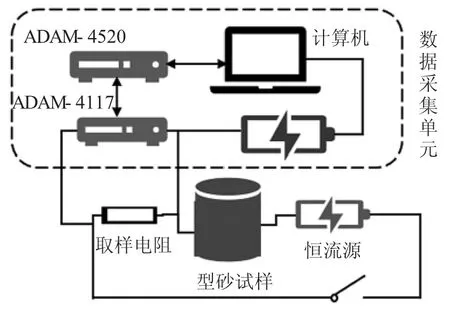
图1 型砂导电特性测试装置
为研究和讨论问题方便,我们用型砂试样施加直流电场作用之初,取样电阻所测电压表征砂样初始直流导电能力;用通电100ms 时取样电阻上的电压降表征砂样直流导电能力变化。
1.2 型砂初始导电能力
在外电场作用下,粘土颗粒表面电荷发生分离,分离的电荷使得粘土颗粒带电。当粘土砂中加入水后,粘土矿物中所含的矿物盐成分在水的作用下溶解发生电离,从而使湿型粘土砂这个溶胶分散体系中含有大量阴阳离子。试验中外加直流电场时,阴阳离子在电场力驱动下发生定向移动,形成电流。形成电流的电荷量与湿型粘土砂中的离子浓度有密切关系,因此,试验中待测砂样内部瞬间电流的产生与外部电势和内部离子浓度均有关系。
由上述分析可知型砂的初始导电能力与三个因素有关:直流激励源的幅值大小,表现为阴阳离子的驱动力;型砂的成分,表现为水对强电解质的电离和粘土胶团的带电性;直流激励时间,通电瞬间可使电荷快速移动,之后阴阳离子移动趋于平衡状态,使得型砂短时间内获得较大初始导电能力。
1.3 型砂导电能力的变化
在外加直流电场作用下,湿型粘土砂中的粘土和水均存在一定程度上的电离过程,电离出来的离子就是砂样导电的媒介。电场中的水被分解为自由水和结合水,自由水含量高于结合水含量。结合水与粘土吸附电场中一部分带电离子,另一部分离子游离于自由水之中。在外部电场作用下,若型砂中水分越少,则自由水含量越少,相应的游离态离子越少,宏观上则表现为待测砂样的测量电阻值越大[3,4];若型砂中水分增加,那么电场中相应的游离态的自由离子增加,宏观上观测到的待测砂样的电阻值会降低。
将被测砂样等效成如图2 所示的RC 串联模型,Rs为等效电阻,Cd为等效电容[5,6]。

图2 砂样等效电路
当待测砂样加入直流激励电场E 时,回路电流为:
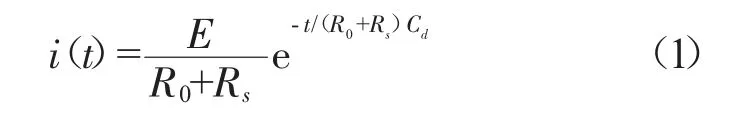
回路中的电流随时间作指数级衰减,其时间常数τ 为:

若忽略取样电阻R0的影响,则电流随时间作指数级衰减的时间常数τ 近似为:

这种回路电流随时间作指数级衰减的过程称为介质的极化过程[7],湿型粘土砂在外加直流电场作用下的极化过程中,60s 时间内取样电阻上的电压降变化曲线如图3 所示。
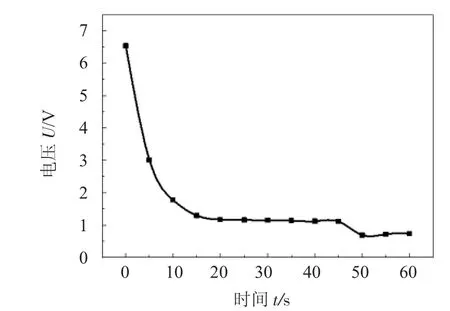
图3 湿型粘土砂导电能力变化曲线
2 组分变化对湿型粘土砂导电特性的影响
当湿型粘土砂的外形尺寸、紧实度和金属电极及激励源电压值确定后,影响湿型粘土砂导电能力的因素主要是砂样组分。
2.1 含水量对湿型粘土砂导电特性的影响
湿型粘土砂中水含量对其导电性影响显著。湿型粘土砂中的强电解质会随着含水量的增加不断发生电离,电离出来的带电离子因含水量不同而产生离子浓度变化。变化的离子浓度对测量回路中的等效电阻Rs产生较大影响[8,9]。若单位体积内自由移动的带电离子数量增加,即离子浓度增加,则待测砂样的导电能力会增强,观测电路中Rs阻值明显降低。
如图4 所示,接通直流激励电源后,提取取样电阻R0上的初始电压值U,该值反映砂样初始直流导电能力;通电100ms 时,提取取样电阻R0上的电压变化值△U,该值反映砂样直流导电能力的变化。
由图4 可见,固定有效粘土含量为6%时,含水量增加,砂样导电能力会增强,电压U 与电压变化△U 均呈现出下降的趋势。这反映了含水量增加导致电离出来的离子数量增加,进一步导致与外加电场方向相反的附加电场增强,宏观上表现为导电能力随之降低。

图4 湿型粘土砂含水量对直流导电特性的影响
2.2 有效粘土含量对湿型粘土砂导电特性的影响
Bidadi[10]的研究表明,粘土在电场力作用下表现出强烈的介电特性,该特性的大小很大程度上取决于粘土中水分的多少,同时受粘土中所含阳离子类型和浓度的影响。因此,有效粘土含量的增加对等效电阻Rs的影响是不确定的,它与粘土中所含电解质的多少和水土的比例有关。
提出的初始直流导电能力和直流导电能力变化与有效粘土含量的关系如图5 所示。
由图5a 可见,在含水量固定的条件下,湿型粘土砂的初始导电能力与有效粘土含量在一定区间内并不是简单的线性关系。含水量为4.0%,粘土含量低于7.0%时,初始直流电压U 随粘土含量的增加而降低,这是因为粘土增加使得大量粘土胶团在电场作用下产生极化作用所致,当粘土含量达到7.0%左右时,极化作用达到最大强度,初始电压值出现极小值点。此后随着粘土含量的增加,自由水相对减少,粘土胶团的极化作用被逐渐削弱,结果造成湿型粘土砂的导电能力逐步回升。由图5b 可见,当有效粘土含量达到某一特定值时,如3.0%和4.0%,由于水土比例适当会使得△U 值达到最大与最小,其后有效粘土含量继续增加使△U 呈现波动式变动趋势。该趋势产生原因有待进一步研究。
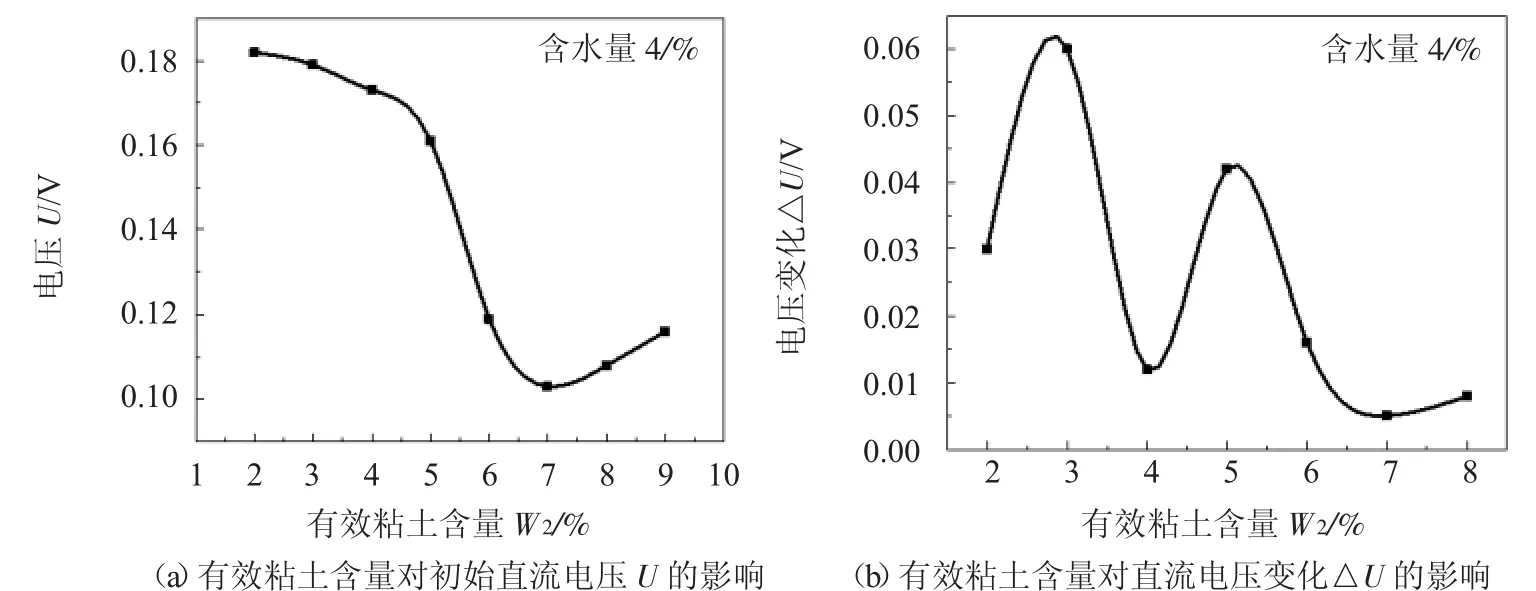
图5 有效粘土含量对砂样直流导电特性的影响
为了进一步研究不同粘土含量和水分含量下砂样导电能力的变化规律,本文将含水量2.0%~6.0%,粘土含量2.0%~9.0%的砂样的初始直流导电能力和直流导电能力变化曲线绘于图6 和图7。
由图6a 可以看出,随着含水量的增加,不同有效粘土含量对应的电压值变化基本一致,均呈现出大幅度下滑后平缓下降的趋势。
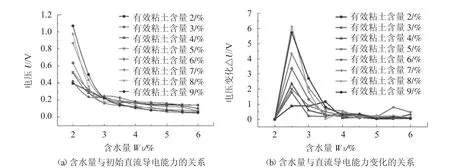
图6 不同含水量下湿型粘土砂导电能力变化
在外加直流激励电场的情况下,有效粘土含量越高,砂样中的粘土胶团越多,粘土胶团可以吸附更多的带电粒子,而这一部分带电粒子大部分由砂样中的水电离分解出来,因而低含水量和高有效粘土含量时,砂样中的带电粒子移向电极愈发困难,观测初始直流导电能力数值高。当含水量逐渐升高时,由水电离出来的带电粒子不断增多,但砂样中总的离子浓度由于高含水量而降低,且水的电离和粘土胶团的吸附有一定限度,不会无限制分解产生带电粒子,因此观测到的电压值走势最终会趋于平缓。图6b 中电压变化规律反映了a 图中的初始直流导电能力变化趋势,b 图中电压变化率大幅度上升与下降体现出砂样中离子电离产生的浓度变化过程。
由图7a 可以看出随着有效粘土含量的增加,不同含水量对应的电压值变化有较大差异。当含水量保持较低数值特别是2.0%和2.5%时,随着有效粘土含量增加,电压变化值非常明显;当含水量保持较高数值时,有效粘土含量的增加所表现出来的电压值反而不明显。原因在于,砂样中含水量保持低值时,在直流激励源的激励下,砂样中自由移动离子不断增加,单位体积内离子浓度提高,相应观测电压值增大。但是随着有效粘土含量和含水量均进一步提高,矿物盐完全溶解后,单位体积内的离子浓度随含水量增加而降低,故而出现高含水量高有效粘土含量的初始直流导电能力低的现象。相应b 中总体上升的趋势符合有限粘土因含水量提高而不断溶解电离的过程,但不同含水量的直流导电能力变化参数的高低亦反映出a 图中的相应差异。
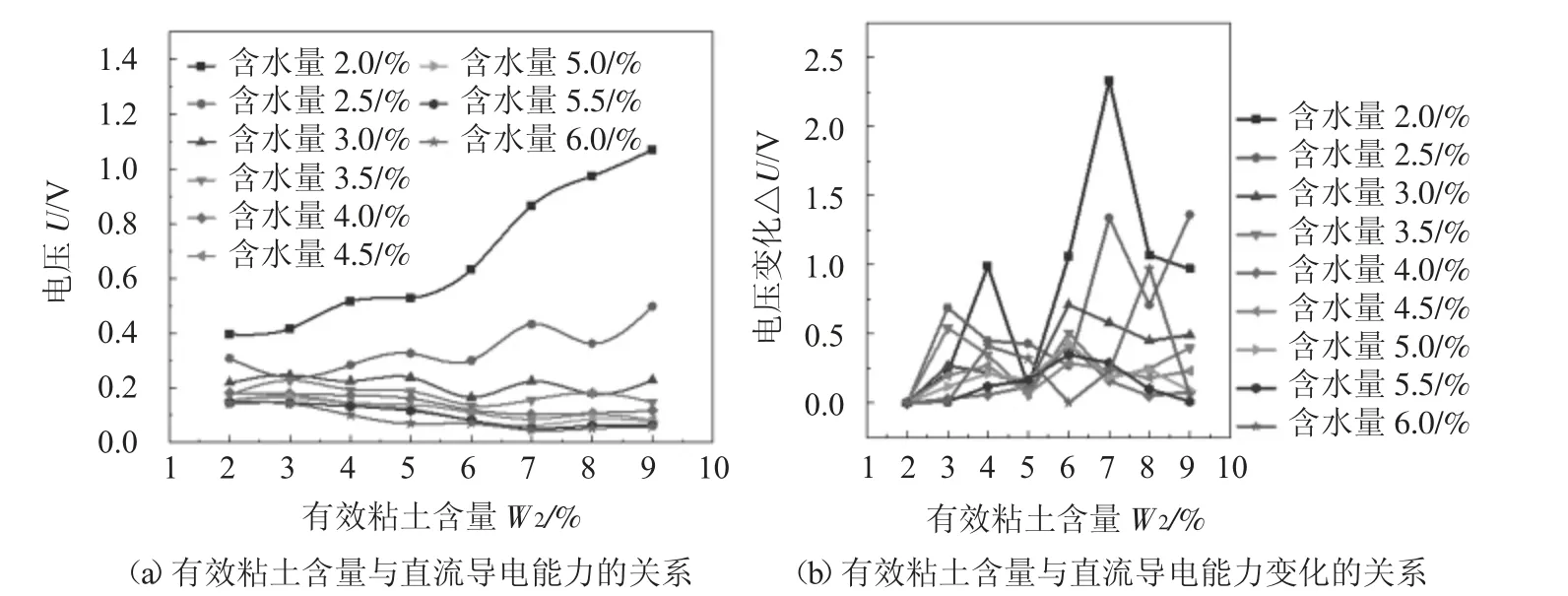
图7 不同有效粘土含量下湿型粘土砂导电能力变化
3 直流导电特性在湿型粘土砂含水量及有效粘土含量快速检测中的应用
3.1 基于人工神经网络的型砂含水量及有效粘土含量求解方法
湿型粘土砂导电机理、导电特性的理论分析及试验研究表明,湿型粘土砂的导电特性表征参数与其主要成分——有效粘土含量和含水量之间有确有依存关系,但是关系比较复杂,当有效粘土含量处于某一数值范围时,导电特性参数与粘土含量出现“V”或“N”形关系,无法依据电压信号求解有效粘土含量,为此本文引入砂样紧实率实现对有效粘土含量求解的“去伪存真”。尽管依据紧实率难以定量准确测定有效粘土含量,但用于多解取舍却有优势。
有效粘土含量与型砂紧实率和初始直流导电能力之间的关系如图8 所示。由图可以看出,有效粘土含量在6%~9%时,同一初始导电能力可能对应不同的有效粘土含量。为此,本文引入有效粘土含量与紧实率的关系曲线。当有效粘土含量在6%~9%时,分别对应不同的紧实率数值,利用这种单调函数关系可以辅助解决有效粘土含量求解的多值问题。

图8 有效粘土含量与型砂初始导电能力和紧实率的关系
将紧实率作为辅助参数引入人工神经网络,本文利用MATLAB 构建如图9 所示的BP 神经网络。
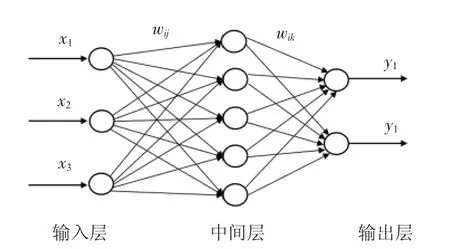
图9 BP 神经网络结构
图9 为BP 神经网络结构,设定输入层的节点为3 个,分别是经过温度补偿和归一化处理的湿型粘土砂初始直流导电能力、直流导电能力变化率和紧实率;输出层为2 个节点,分别是湿型粘土砂的含水量和有效粘土含量;隐含层节点选为6个。BP 神经网络采用Sigmoid 函数作为中间层和输出层的传递函数,采用Levenberg-Marquardt 算法来优化训练[11],测试训练和结果验证的数据样本共为100 个。
3.2 人工神经网络训练与检验
本文对含水量1.5%~6.0%、有效粘土含量2.0%~9.0%的湿型粘土砂进行了80 次实验,随机选取40 次结果作为训练样本,其余为测试样本。实验测量用的湿型粘土砂包含石英砂、钠基粘土、煤粉(4.0%)和水。实验中采用红外线烘干法测得真实含水量,有效粘土含量采用计算加入量数据。经过BP 神经网络训练后,用10 个样本对该方法的准确性进行检验,为了能定量地评价和分析BP神经网络模型的计算误差和训练效果,本文采用3 个定量指标,即MAE(平均绝对误差)、MSE(均方误差)、RMSE(均方根误差)[12]。它们的计算公式如下:
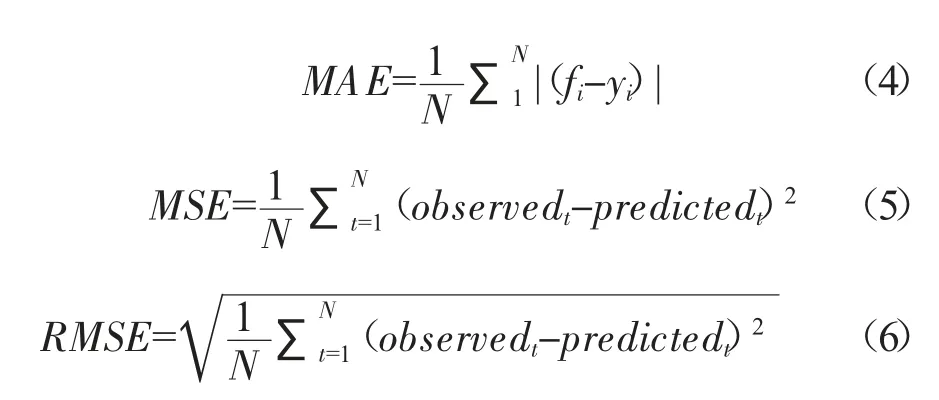
注:fi为预测值、yi为真实值、observedt为真实值、predictedt为预测值。
可以证明平均绝对误差、均方误差和均方根误差接近0 时,表示神经网络模型的计算误差小,训练效果较好。本文BP 神经网络训练效果如表1所示。

表1 BP 神经网络模型对训练样本的计算误差
表2 给出了采用神经网络算法及标准检测方法所得有效粘土含量和含水量的测定结果,结果数据表明BP 神经网络通过初始直流导电能力、直流导电能力变化和紧实率来计算含水量和有效粘土含量可行。
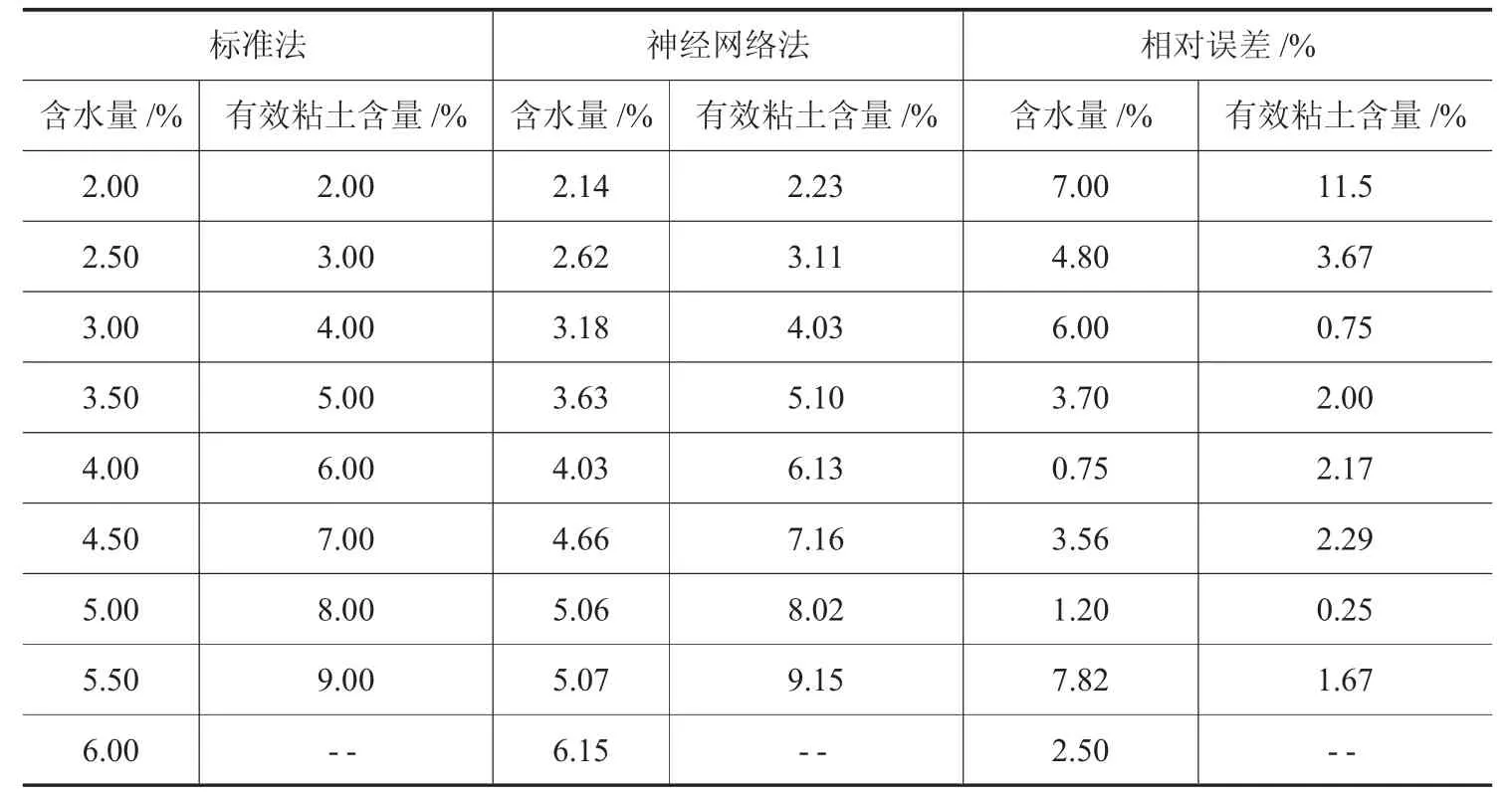
表2 神经网络算法及标准检测方法测量含水量和有效粘土含量的结果
4 结论
(1)湿型粘土砂在直流电场作用下,粘土和水会发生一定的电离,进而导致砂样中离子浓度变化,最终影响了砂样的等效电阻Rs的等效电容Cd,使砂样两端电压随通电时间呈非线性衰减——极化现象。当含水量和有效粘土含量很低时,直流电源激励下的湿型粘土砂样可呈现初始导电能力极大值,随含水量或有效粘土含量升高,初始导电能力将逐渐减小,直至出现初始导电能力极小值。导电能力变化值随有效粘土含量增加呈现波动下降趋势,当有效粘土含量固定而改变含水量时,型砂导电能力随含水量升高,呈现大幅度下滑接着小幅度衰减的趋势,导电能力变化值亦呈同样趋势。
(2)本文所选择的BP 人工神经网络包括输入层、隐含层和输出层,输入节点分别为砂样初始电压值、电压变化值和紧实率,输出节点分别为型砂含水量及有效粘土含量,中间层节点数为6 个。采用Levenberg-Marquardt 算法对100 个数据样本进行优化训练,最终含水量训练结果:相对最大误差为7.82%,相对最小误差为0.75%;有效粘土含量训练结果:相对最大误差为11.5%,相对最小误差为0.25%,训练结果表明BP 神经网络通过初始直流导电能力参数、直流导电能力变化参数和紧实率可求解含水量和有效粘土含量。
(3)应用最简单的直流激励法,选取合适的输入参数和人工神经网络,可以实现湿型粘土砂含水量及有效粘土含量快速检测,经过进一步完善,有望用于实际生产中的型砂质量控制。

