基于深度强化学习的分布式电驱动车辆扭矩分配策略

孔泽慧 樊杰

（1.广西机电职业技术学院，南宁 530007；2.中国汽车工程研究院股份有限公司，重庆 401122）

主题词：分布式驱动 电动汽车 深度强化学习 扭矩分配

1 前言

分布式驱动电动汽车（Distributed Drive Electric Vehicle，DDEV）具有响应快、加速性好、多自由度、控制灵活等独特优势，在提升车辆操纵稳定性、安全性和经济性等方面极具潜力。

前、后轴扭矩分配策略是DDEV发挥上述潜力的关键所在，如：Nam等为提升车辆经济性提出了面向急加速场景的车轮防滑控制策略；孟彬运用动态方法寻找轮毂电机的高效区，获得了前、后轴扭矩分配系数；X.Yuan等提出了一种扭矩分配策略，解决了低需求扭矩下系统的低效问题。但上述方法仅面向驱动工况，未考虑DDEV 的制动能量回收。为充分发挥电驱动系统在可再生制动领域的独特优势，Sun 等运用非线性模型预测控制方法设计了DDEV的再生制动扭矩分配策略，J.Zhang 等综合考虑驱动、制动场景，设计了再生制动和摩擦制动的协调控制策略。虽然上述研究将电机的制动能量回收也纳入优化范畴，但扭矩分配以经济性为目标，未考虑制动稳定性约束，存在应用局限性。

扭矩分配策略依据算法可分为基于规则和基于优化的方法。基于规则的方法因具有高可靠性而广泛应用于实车，但应用效果受工况影响较大；基于优化的方法在变量可行域中以最小化成本函数为目标求解最优控制变量，优化效果远优于基于规则的方法，因此日益受到重视。目前常用的优化方法包括动态规划、粒子群算法和强化学习等。其中，强化学习作为当代前沿智能算法的一类典型代表，在控制领域已取得了令人瞩目的应用成果，如何洪文等运用深度强化学习方法为功率分配型混合动力电动客车设计了能量管理策略，其燃油经济性与基于动态规划的全局最优结果近似度超过90%。

考虑到强化学习在控制领域的强大应用潜力，本文提出一种基于深度强化学习的DDEV前、后轴扭矩分配策略。在保证制动稳定性的前提下，以车辆的总需求扭矩和车速为状态输入，前、后轴扭矩分配系数为输出，利用深度神经网络建立状态输入到控制输出的最优映射，并通过与传统固定系数的前、后轴扭矩分配策略对比，验证算法的有效性。

2 DDEV车辆建模

DDEV的结构如图1所示。车辆由4个独立的电机驱动，每个电机连接1 个离合器，并通过轮边减速器与车轮相连。其中，、分别为质心与前、后轴的距离。

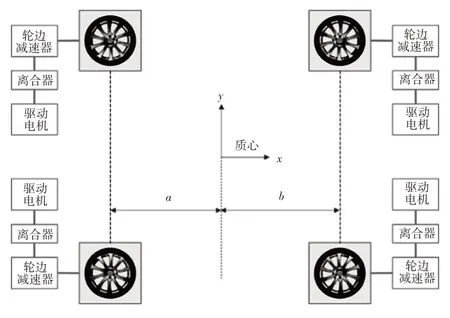
图1 DDEV结构示意

为了求解控制策略，需要建立能够准确模拟车辆动态响应的物理模型。本文采用商业化车辆动力学软件CarSim内置的车辆模型，包括驾驶员模型、悬架模型、轮胎模型，其中考虑了轮胎力饱和效应、轮胎迟滞效应、轮胎载荷转移效应等。其他车辆子系统，包括驱动电机、机械制动系统、电池模型等，对其进行数学建模，并搭建MATLAB∕Simulink模型。

2.1 电机模型

电机模型可以表示为：

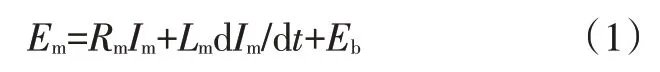
式中，、分别为电机的电压和电流；、、分别为反电动势、电枢电阻和电枢电感，并且：

式中，、均为电机常数，取决于电机结构、绕组数量和铁芯材料属性等；为电机转速；为电机扭矩。

另外，电机的电压和电流需要满足：

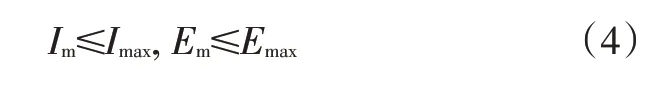
式中，、分别为电机的最大电流和最大电压。

根据文献[12]的测试结果，绘制如图2 所示的电机效率MAP，为简化计算，认为电机在制动时的效率与其在对应状态下的驱动效率相同。

图2 电机效率MAP

电机功率是输出扭矩、电机转速和电机效率的函数，可以表示为：

式中，为电机效率，可以根据图2由电机扭矩和电机转速插值获得，电机扭矩和转速可以通过电机控制器的传感信号获取。

2.2 机械制动模型

电机的制动力矩虽响应迅速，但十分有限，因此在大制动强度下需要机械制动系统参与制动。本文假设电制动和机械制动能够实现制动力矩的连续调制，力矩响应可以近似为如下一阶系统：

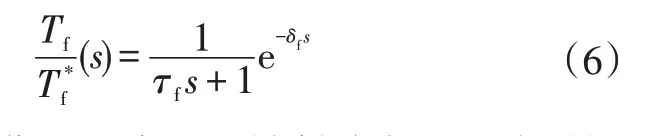
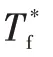
2.3 电池模型

本文采用锂离子动力电池作为能量源，一阶RC 电路电池模型为：

式中，为一阶RC网络端电压；、分别为RC网络的极化电容和极化内阻；为激励电流；为电池容量；为电池端电压；为电池开路电压；为欧姆内阻。

根据安时积分规则，电池荷电状态（State of Charge，SOC）与电池容量和激励电流存在以下关系：

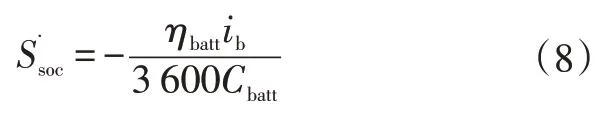
式中，、分别为电池的荷电状态和充放电效率。

以SOC的多项式函数进行建模：

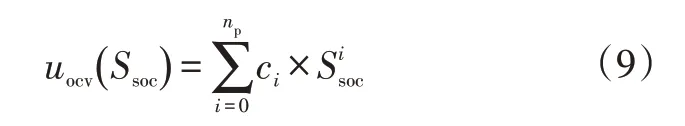
式中，c为第阶SOC分量对应的多项式系数；为多项式的阶数，本文取=5，即认为是的五阶多项式函数。

部分整车参数如表1所示。

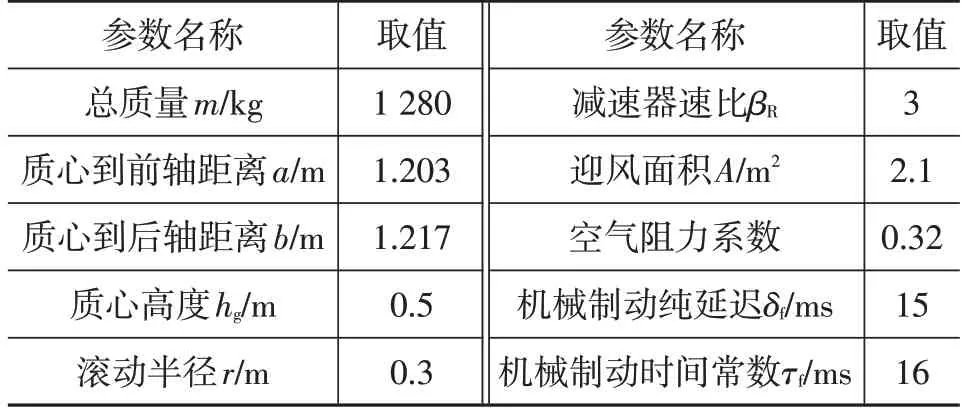
表1 车辆基本参数

3 基于深度强化学习的扭矩分配设计

强化学习的思想是通过与环境的试错交互，基于观测值及对系统行为的分析提高系统性能，通常以最大化累计回报函数为目标，获得最优控制策略。

-learning 是著名的强化学习方法，当给定控制策略时，在状态s下执行动作a时的动作值函数可以表示为：

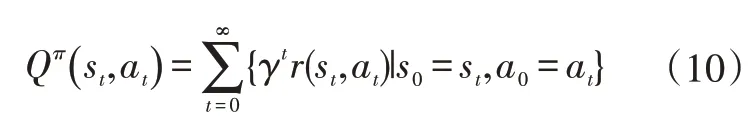
式中，为[0,1]范围内的折扣因子，表示将未来回报折算到当前时间点的回报折算值；为单步回报；Q为动作值函数，表示在当前状态s下，执行动作a后的长期期望累计回报。

最优动作值函数定义为：

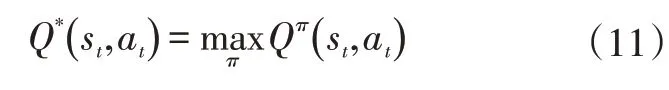
可以通过选择最大化值的动作来获得最优控制策略：

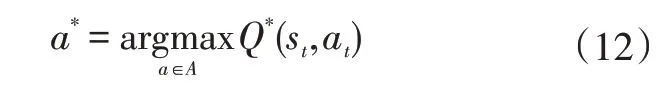
式中，为动作变量的可行域空间；为执行的动作；为获得最优值函数的动作。

传统的-learning 通过离散化状态和动作参数来获得从状态到动作的最优控制策略，但针对DDEV扭矩分配，由于系统的状态（需求扭矩、车速）为连续输入，一方面，离散化会影响最终优化策略求解的精度，另一方面，过度的离散化也会带来“维数灾难”，增加运算负担。因此，为了对包含连续状态的控制问题应用learning，可运用深度强化学习算法，通过神经网络实现从连续状态到动作值函数的映射：

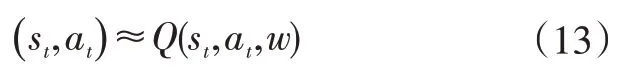
式中，为深度神经网络的参数；(s,a,w)为从状态s和动作a到动作值函数的映射。

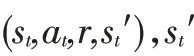
本文定义需求扭矩和电机转速组成的二维向量为系统状态，即=(,)，系统的动作为前、后轴的扭矩分配系数，这里定义为前轴扭矩在总驱动扭矩中的占比，并且假定同一轴上的2个电机输出扭矩相同，即

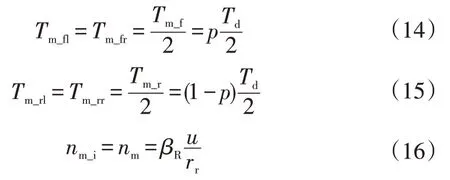
式中，、、、分别为左前轮、右前轮、左后轮、右后轮的扭矩；、分别为前、后轴的扭矩；为轮边电机转速；=1,2,3,4 分别表示左前、左后、右前、右后轮；为车速；为车轮的滚动半径；为轮边减速器的速比。

控制目标为整车的经济性最优，由于-learning 算法通常最大化累计期望回报，而本文的优化目标是最小化瞬时能耗，因此定义瞬时回报为系统瞬时能耗的相反数：

式中，为指示函数，驱动状态时=-1，制动状态时=1。

本文设定神经网络具有4个隐含层，隐含层之间为全连接结构，每层拥有500 个神经元，神经元的激活函数为，输入层有2个神经元，分别代表状态向量中的需求扭矩和电机转速，输出层有11 个神经元，将在[0.5,1.0]范围内均分为10 等份，11 个神经元依次代表取0.50、0.55、0.60、…、0.95、1.00 时对应的动作值函数。的最小值为0.5，即前轴的扭矩始终不低于后轴，原因是前驱车辆具有不足转向特性。

另外，系统必须满足的约束条件还包括：

式中，为轮边电机扭矩；=1,2,3,4 分别表示左前、左后、右前、右后轮；、分别为最大扭矩和最大转速。

当车辆处于制动状态时，还需要满足制动稳定性约束。理论上，为了达到最大制动效能，前、后轴应同时达到“抱死”条件，此时前、后制动力和满足图3所示的I曲线，即

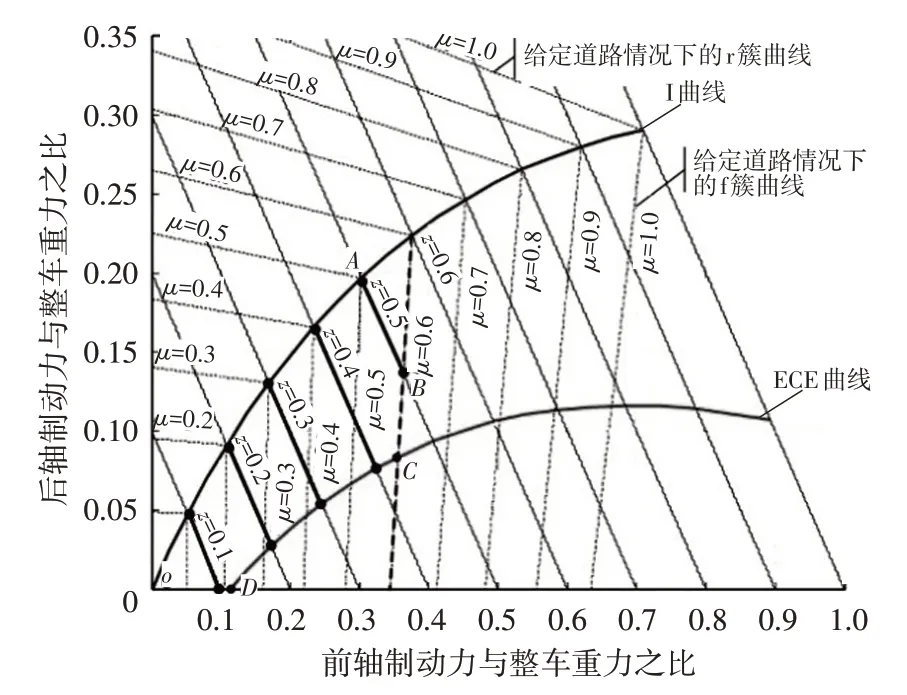
图3 制动稳定性边界

式中，为车辆质心高度；为轴距。

然而，实际情况下很难实现前、后轴同时达到“抱死”，为保证车辆的稳定性，通常允许前轴较后轴先抱死，即前、后制动力分配系数应该在I曲线下方。

另外，欧洲经济委员会（Economic Commission for Europe）规定了后轴最小制动力以避免前轴过于容易达到“抱死”且保证制动距离满足要求。根据规定，制动强度和路面附着系数应满足：

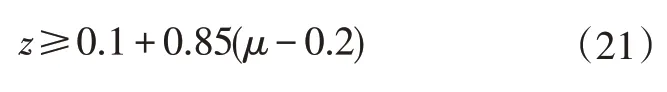
因此，可以得到如图3所示的ECE曲线，其表达式为：

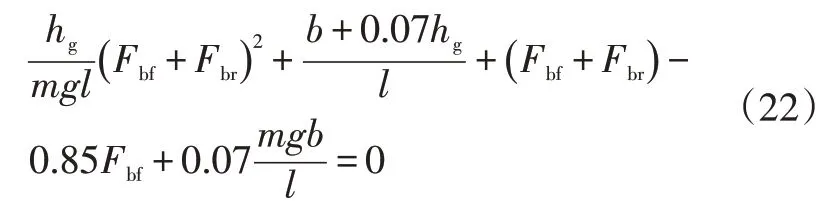
另外，美国州公路工作者协会研究表明，在紧急情况下，良好路面上的制动强度可达0.55，而一般情况下的制动强度通常低于0.35。因此，本文将制动强度限定在0～0.5范围内。如果制动强度超过0.5，将被认为是紧急制动，为保证制动的可靠性，可完全采用机械制动。

根据上述分析，从制动稳定性角度看，的可行域为图3中围成的区域。

本文采用的深度强化学习相关网络参数如表2 所示，详细算法流程为：

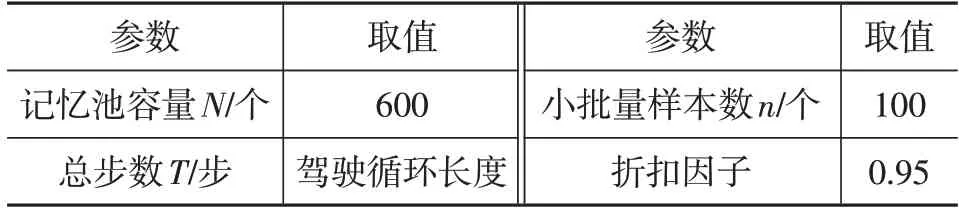
表2 深度强化学习参数

基于深度强化学习的DDEV 扭矩分配计算流程如图4所示。

图4 基于深度强化学习的DDEV扭矩分配计算流程

4 仿真结果及讨论

4.1 NEDC工况试验仿真

新欧洲驾驶循环（New European Driving Cycle，NEDC）工况下，基于深度强化学习求解的驱动和制动状态下的最优扭矩分配MAP 如图5 所示：当需求扭矩（绝对值）较低时，为了避免电机在低扭矩情况下进入低效区，通过前轴电机产生驱动力或进行制动能量回收；当需求扭矩较高时，扭矩近似在前、后轴间均等分配。

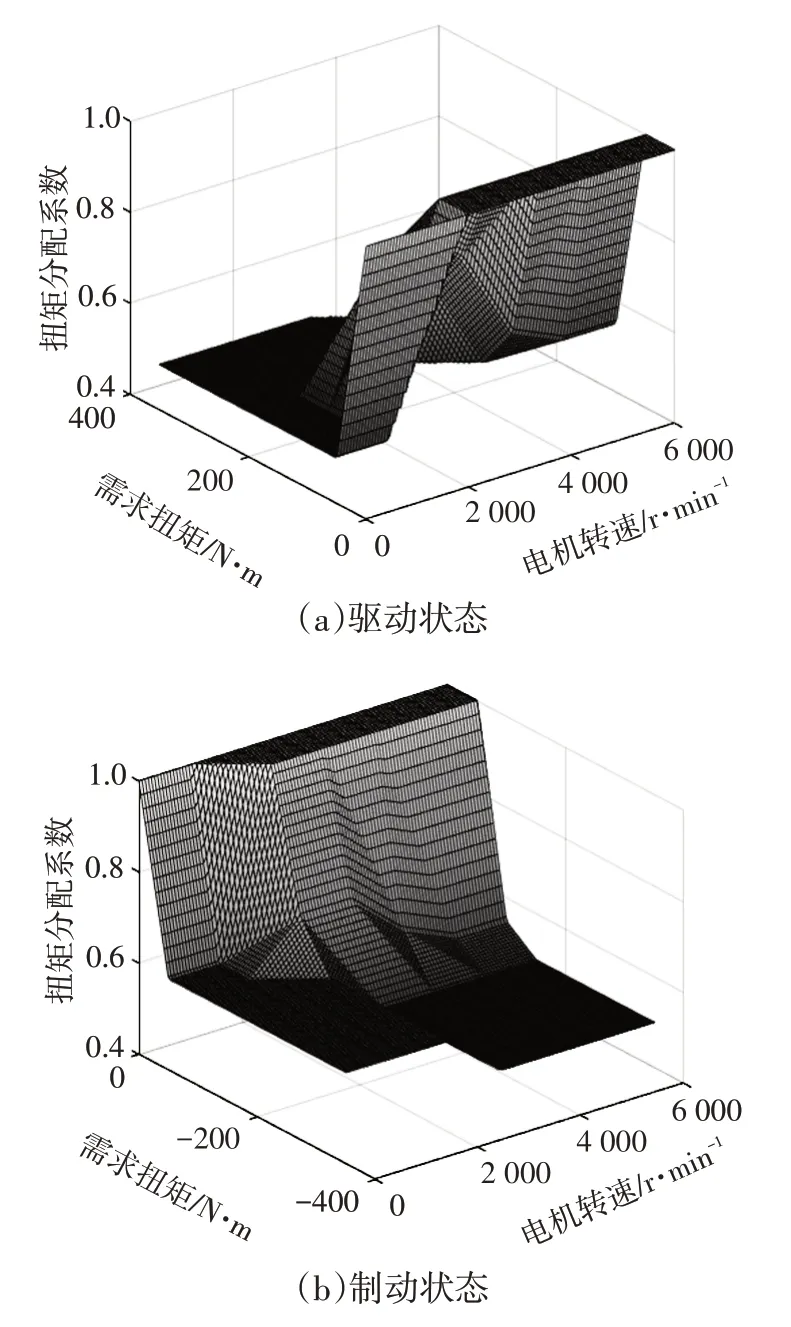
图5 基于深度强化学习求解的最优扭矩分配MAP

为了验证所提出的基于深度强化学习的DDEV 扭矩分配策略的经济性优势，采用传统扭矩分配策略作为对比基准。传统扭矩分配策略在驱动状态下，力矩在4 个车轮间通常平均分配，在制动状态下，制动力在前、后轴间按照固定比分配。为了保证车辆的制动稳定性，一般要求车辆的前轮制动力稍大于后轮制动力，取=0.6。制动时优先采用再生制动，如果电机制动力矩能够满足制动需求，则完全由电机制动，否则，电机按照最大力矩进行制动，所需的剩余制动力由机械制动补足。

通过CarSim 和MATLAB∕Simulink 联合进行NEDC工况仿真，为了量化对比，引入以下指标：

a.牵引效率，用于评价驱动系统的能耗水平：

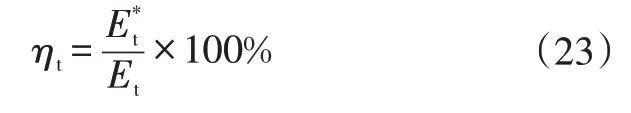
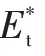
b.再生制动率，用于评价再生制动系统的能量回收能力：

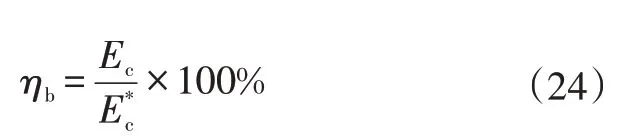
c.节能率，用于评价整车的节能水平：

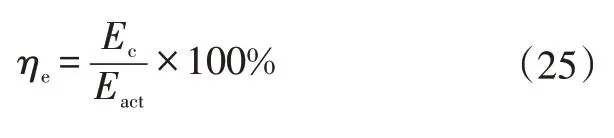
式中，=-。

在如图6所示的NEDC工况下分别进行2种控制策略的仿真。设定电池初始SOC 为80%，2 种扭矩分配策略下的电机扭矩输出和驱动∕制动功率对比如图7所示，可以看出：在NEDC的市区工况下，2种控制策略的输出基本一致；在高速、市郊工况下，由图7a和图7b可知，基于深度强化学习的控制策略更倾向于使用前轴驱动；图7d表明，基于深度强化学习的扭矩分配可节省超过10%的驱动功率，同时制动回收功率可增加近10%。

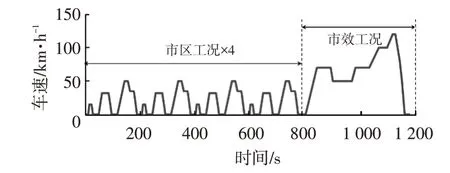
图6 NEDC工况

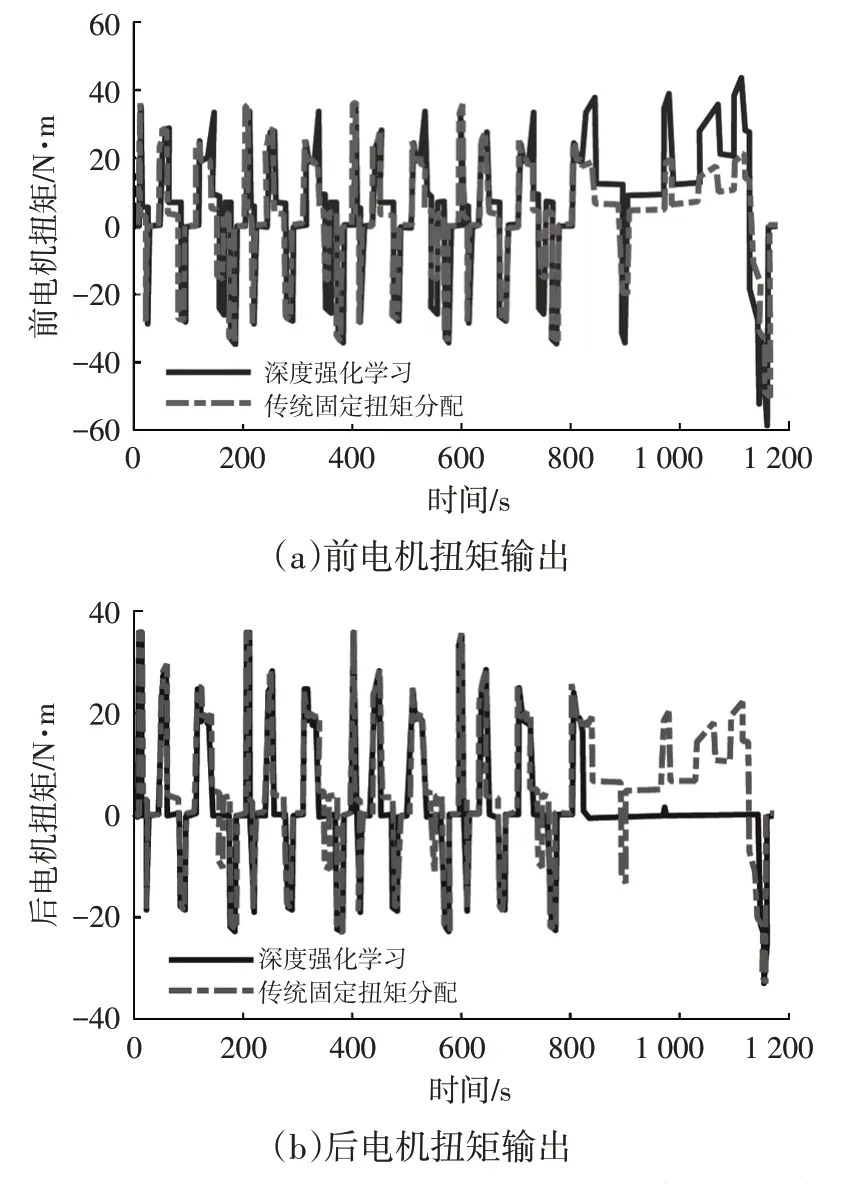
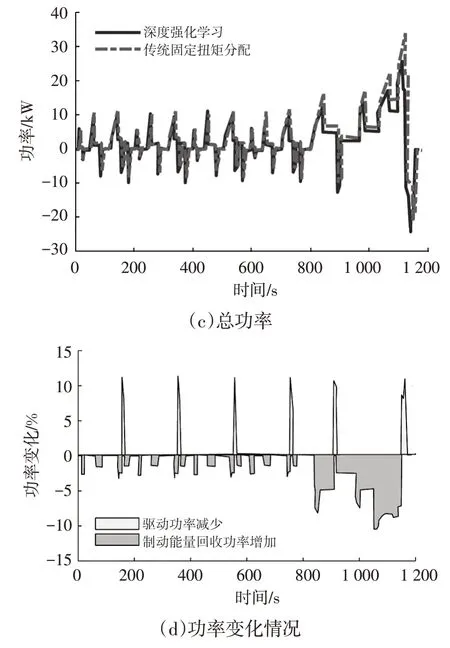
图7 2种扭矩分配策略结果的对比

表3和表4分别对比了2种控制策略的能耗特性和评价参数。与传统方法相比，深度强化学习策略对应的牵引效率和再生制动率均有所提高，其中牵引效率提高了4.18百分点，再生制动率提高了4.92百分点。除此之外，2种策略下初始SOC均设定为80%，在结束时，强化学习对应的SOC比传统策略高出3.96百分点。由于上述在驱动和制动工况下的改善，车辆节能率提高了3.48百分点。

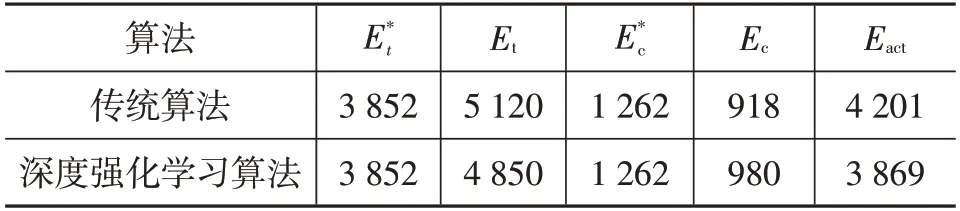
表3 能耗特性对比 kJ

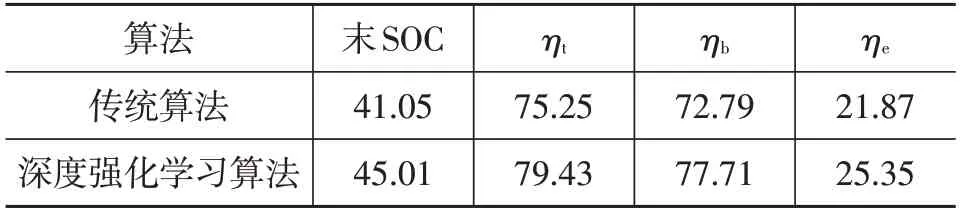
表4 评价参数对比 %

4.2 对开路面大强度制动硬件在环测试

为了验证所提出的控制策略能否保证车辆良好的制动稳定性，通过硬件在环测试进行对开路面大强度制动测试，对开路面左、右侧附着系数分别设定为0.2 和0.5，制动强度取0.5（即所提出控制策略允许的制动强度上限值）。基于RT-LAB和MotoTron的硬件在环仿真测试平台如图8 所示，在该平台中，基于深度学习算法获得制动扭矩分配MAP并作为扭矩分配原则，MotoTron控制器接受需求扭矩和电机转速信号，根据制动扭矩分配MAP 插值获得扭矩分配系数，RT-LAB 中包含分布式车辆的系统模型，接受MotoTron控制器发送的扭矩分配信号，同时输出需求扭矩和电机转速。

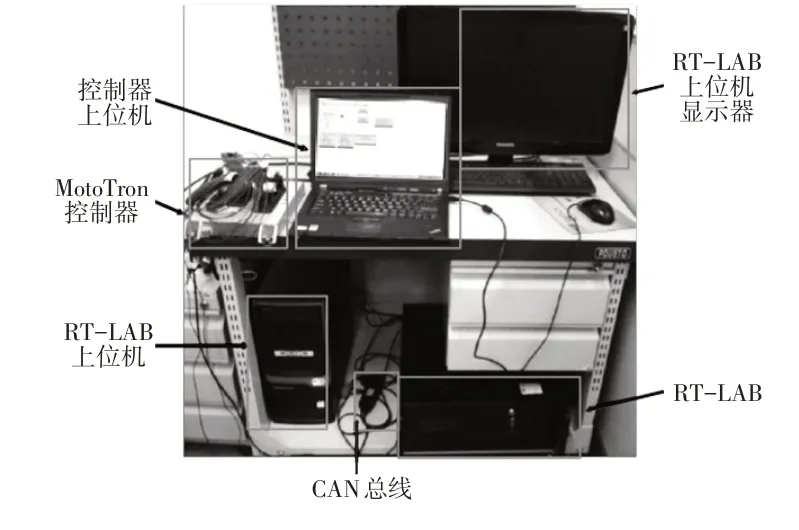
图8 基于RT-LAB和MotoTron的硬件在环测试平台

传统策略和基于深度强化学习的策略下4 个车轮的滑移率如图9 所示，可以看出：对于传统扭矩分配策略，在施加制动信号后，左侧车轮先后进入低附着系数路面，滑移率迅速提高，最高可达到4%左右，由于车辆在高滑移率时，附着率较低，导致路面可对左侧车轮提供的最大附着力降低，从而使整车左侧处于易打滑状态，而右侧车轮处于低附着良好状态，左、右侧附着力的不平衡使车辆处于不稳定状态；而本文提出的控制策略，由于增加了制动稳定性约束，左侧车轮的滑移率一直控制在20%附近，此时车轮具有较为理想的附着特性，车辆的稳定性良好。

图9 2种扭矩分配策略滑移率的对比

5 结束语

本文面向分布式驱动车辆，提出了基于深度强化学习的扭矩分配策略，在保证车辆制动稳定性的前提下，以经济性为目标，获得了前、后轴扭矩的最优分配系数。验证结果表明：在NEDC 工况下，相比于传统的固定前、后轴扭矩比的控制策略，提出的控制策略可以实现牵引效率和再生制动率的提高，节能率提高了3.48百分点；在对开路面大强度制动硬件在环测试中，所提出的控制策略能够将低附着系数路面车轮滑移率控制在20%附近，保证了车辆的制动稳定性。