多技能项目调度问题研究综述
胡振涛, 崔南方, 胡雪君, 张 艳
(1. 华中科技大学管理学院,湖北武汉 430074;2. 湖南大学工商管理学院,湖南长沙 410082;3. 东莞理工学院经济与管理学院,广东东莞 523808)
1 引 言
多技能项目调度问题(multi-skilled project scheduling problem,MSPSP)中的资源可同时具备多种技能,以芯片研发项目中的研发人员为例,掌握模拟IC 设计技能的员工,也往往会了解一些模拟版图实现的技能,这种多技能资源的存在对项目的计划制定者而言,既是机遇也是挑战.
多技能使资源的分配更加灵活,这不仅能丰富项目计划的多样性,还能在项目面临不确定风险时,为管理者提供更为灵活多变的应对措施.如Hegazy 等[1]研究了单技能项目和多技能项目的调度问题,结果表明项目管理者在调度时考虑多技能策略能有效地减少工期降低成本. Arashpour 等[2]则指出,多技能员工有助于降低项目周期、提高项目产出、提升资源均衡水平,并鼓励企业对员工进行适当的跨技能培训.此外,陈蓉等[3]在研究人员随机离职的多技能项目调度问题时提出,当项目实施过程中出现人员离职时,可根据技能特征选择与离职员工相近的员工补缺,以降低这类不确定事件的影响.
然而, 多技能资源的出现也为项目调度带来了更大的挑战.在单技能项目调度中, 由于活动所需资源的类型明确,资源技能单一,项目的调度计划一旦确定,资源分配方案便随之确定,并不涉及复杂的资源指派问题.而在MSPSP 中,资源的多技能属性使得不同种类的资源之间存在相互替代的可能性,活动所需要的技能可由不同的资源执行. 因此, 即便已经生成了项目的调度计划, 依旧需要解决资源的指派问题. 所以MSPSP 是调度问题与指派问题的组合,求解更加复杂,属于NP-hard 问题[4].
近年来,越来越多的学者开始研究MSPSP,而目前尚缺乏对这些成果的系统梳理. 本文以“柔性+项目调度”、“多技能+项目调度”和“flexible+project scheduling”,“multi-skill+project scheduling”为关键词,分别在知网、万方、维普等中文数据库,Elsevier ScienceDirect,Web of Science,SpringerLink,EBSCO 等英文数据库检索了相关文献,以2000 年~2020 年为限,经过相关性及创新性筛选后,按文献公开年份统计结果见图1.可以看出,学术界对MSPSP 的关注度在逐渐提升. 因此,有必要对MSPSP 的国内外相关研究成果进行归纳整理,为本领域的后续研究提供支持.
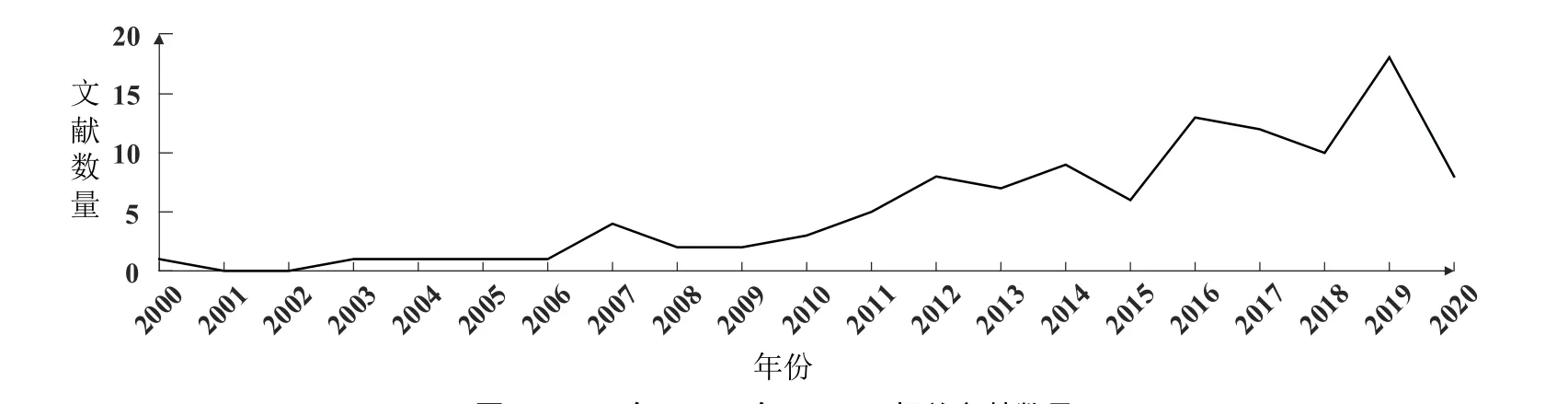
图1 2000 年~2020 年MSPSP 相关文献数量Fig.1 Quantity of literatures on MSPSP in 2000~2020
2 基于MSPSP 建模的研究综述
2.1 问题描述与基础数学模型
基础MSPSP 主要包含如下要素: 活动参数、资源参数、技能参数及其它相关参数. 其中项目网络采用节点式表示, 共包含n个活动节点, 起始节点1 和终止节点n代表虚活动; 活动之间存在工序约束;以G={V,E}表示项目网络,其中V={1,2,...,n}表示活动集合,E为有向弧,表示活动的工序约束;活动i的工期为di,对技能l的需求表为TFil;资源具备多技能,每个资源都至少具备一种项目所需求的技能,R={1,2,...,K}表示资源集合,资源总量为K;F={1,2,...,L}表示技能集合,技能种类为L. 相关符号汇总于表1.

表1 MSPSP 相关参数汇总Table 1 Summary of the parameters in MSPSP

续表1Table 1 Continues
MSPSP 需要解决的是, 在一定的环境下, 如何对活动排程并为之分配资源, 以满足预设的目标.所以,MSPSP 的主要决策内容为:活动的开始时间、活动所使用的资源以及资源在对应活动中所执行的技能.根据现有文献,模型中决策变量的构建可分为两类. 第一类为含有时间索引的决策变量,其最常用变量形式为

由式(1)或式(2)可以确定项目活动的排程,由式(3)可以推导出相应的资源分配方案.据此,含有时间索引的MSPSP 数学模型(I)如下

其中式(4)表示目标函数; 式(5)表示各活动的执行时间必须得到满足; 式(6)表示活动工序约束不可违背;式(7)表示资源只可执行其所掌握的技能;式(8)表示资源在某一时刻最多只能执行一种技能,且最多只能分配给一个活动;式(9)表示各活动的技能需求必须得到满足,且不会被分配到过多的资源;式(10)表示活动在执行过程中不可被中断;式(11)表示决策变量的可行域.
第二类决策变量在构建时不以时间为索引,而是引入了活动的时序关系,最常见的变量形式为

Si表示活动i的开始时间,
由决策变量(12)可以确定项目活动的排程,由决策变量(14)可以得出项目的资源分配方案.由此可归纳出含有时序关系的MSPSP 数学模型(II)如下

其中式(15)表示目标函数; 式(16)表示活动的工序约束不可违背; 式(17)表示资源只可执行其所掌握的技能;式(18)表示各活动的技能需求必须得到满足,且不会被分配到过多的资源;式(19)表示资源在一个活动中最多只能执行一种技能;式(20)表示两个活动不可互为前序;式(21)表示并行的活动不可使用同一资源;式(22)表示决策变量的可行域.
2.2 目标函数
项目工期是MSPSP研究中最常见的目标,一般是指在确定性环境下所生成的调度计划的工期,其典型的数学表达为

项目成本是项目管理者关注的另一个重点. 在MSPSP 研究中,考虑的成本主要有三类: 和多技能资源有关的成本CR[57,79],和工期有关的成本CT[65],以及固定成本CF[91]. MSPSP 中最小化项目成本可总结为

此外, 还有以资源均衡[42]、项目净现值[84]、调度计划鲁棒性[53]等为单目标, 以“项目工期+项目成本”[8]、“项目工期+工作时间均衡”[92]等为多目标的MSPSP 研究,整理相关文献可知,MSPSP 的目标可分为三类: 时间类目标、成本类目标和资源类目标.
时间类目标的研究背景可分为确定性环境和不确定环境两种. 确定性环境假设项目的内容、项目的活动时间、资源的状态等都是确知且不变的,如何在工序约束、资源约束及时间约束之下,得到一个项目周期最短的调度计划是这类问题研究的重点. 而不确定环境,则假设项目中存在不确定因素,且这些因素会干扰调度计划的实施,如何在计划制定期便考虑这些不确定因素,以保护项目如期进行是这类问题研究的核心,其最常见的目标形式为最大化按时完工率、最小化项目期望工期等[94].
成本类目标具有鲜明的项目特征,不同的项目其成本构成会存在较大差异.如在研发项目中,研发人员的工资、奖金、分红以及培训费用等资源使用成本是研究的重点. 而在一些具有严格交付期的大型工程项目中,更受关注的则是和工期有关的惩罚性和奖励性成本等.
资源类目标在多技能项目调度问题研究中,有显著区别于一般项目的特点. 在项目计划阶段,多技能资源的指派方案更多,这使得资源均衡问题变得更复杂,但同时也使其具备了更大的优化空间. 在项目实施阶段,当发生计划外的不确定事件时,常常会进行反应性的资源重调度,而资源的多技能特征也使得这种反应性调度更加灵活. MSPSP 的变量形式及目标见表2.

表2 MSPSP 的变量形式及目标Table 2 Models and objectives in MSPSP
2.3 约束条件
在现实中,不同的项目具有不同的内部特征,也面临着不同的外部环境. 项目间的这些差异在数学模型中表现为不同的约束条件,并由此产生了许多MSPSP 的变体.以下将从项目环境、活动以及资源–技能三个角度,介绍多技能项目在现实中所面临的不同状况,以及在构建模型时所对应的约束条件.
1)项目环境类约束
在MSPSP 研究中, 因自然环境、社会环境及项目内部环境变化而导致的模型中某些预设参数出现变化的情况,被称为不确定环境的MSPSP.项目不确定性的来源主要有两个,活动和资源. 其中最常见的是活动时间不确定[53],也即模型中di不再是常数,而是一个随机量. 此外还有活动需求的不确定[34],即模型中的TFil为随机量;活动存在不确定[52],即在项目网络中活动数量有增加或减少的可能;以及活动实现不确定[55],即活动完工后存在返工的可能.资源的不确定情况可分为两类,第一类为资源状态不确定[3],如员工离职、设备故障等导致某些资源处于不可用状态;第二类为资源效率不确定,如资源的技能水平存在波动等.
此外,在实际中项目的执行或多或少地会与其它项目产生联系,因此部分学者考虑了多项目环境(multiproject)下的MSPSP.多项目调度的研究可分为普通多项目调度和项目组合(project portfolio)调度,普通多项目调度假设各项目有互相独立的项目管理者,项目间利益独立、信息独立,唯一的联系是共享有限的全局资源. 而项目组合调度则假设各子项目不仅共享资源还具有共同的战略目标,并且子项目与子项目之间还可能存在工序约束.
现代项目面临着愈发复杂的内外环境,因此不确定环境下的鲁棒项目调度研究也成为近些年来的研究热点[95]. 然而多数研究还停留在一般单技能项目的层面,而很少有对多技能项目鲁棒调度的研究.此外,很多现实的多技能项目,如研发项目等,都是以项目组合的形式实施进度管理的,而学术界对于多技能项目组合调度问题的关注还不足.
2)活动类约束
在最基本的MSPSP 中, 活动工序服从结束–开始(finish-start, FS)的约束类型, 也即紧前活动结束之后,后续活动才可开工. 而在现实项目中,活动工序之间的约束类型往往更加复杂,即广义优先关系(generalized precedence relations)[69],如SS(start-start),SF(start-finish)和FF(finish-finish)等.
多模式(multi-mode)指的是活动的执行可从多种模式中选择[65],不再是消耗固定量的资源、花费固定量的时间,一般情况下,可通过增加资源数量来减少活动的工期,也可通过延长活动工期来减少资源的投入.表现在模型中,活动对技能的需求量TFil及活动工期di都不再是定值,且TFil与di具有相关性

实际上,多模式项目调度问题更一般化的情况是离散时间/资源平衡问题(discrete time/resource trade-off problem,DTRTP),它假设各活动有固定量的工作内容(work content/workload),当投入资源与花费时间的乘积等于工作内容时活动才可完工[47].
活动可中断(preemptive)也被部分学者称为任务可拆分[6],区别于传统项目调度问题中活动一旦开始必须持续到完工的要求,可中断约束允许活动在执行过程中暂停,并在之后任意时刻开始. 在研究MSPSP 时,若加入活动可中断约束,会引出很多与中断–再开始这一过程有关的问题,如活动中断–再开始的过程是否消耗额外的资源与时间[15],活动重新开始时会否产生额外成本[37],活动中断再重新开始时是否可更改原本的资源分配方案[6]等. 此外,还有关于活动可中断更加一般性的假设: 如项目中仅有部分活动可中断,且在中断以后,相应活动所使用的资源并非全部都可被释放[70]等.
3)资源–技能类约束
项目所涉及的资源一般可分为可更新资源和不可更新资源两种,MSPSP 中的多技能资源多是指可更新资源,且一般情况下,资源的总量为定值,资源之间相互独立. 而文献[20,21]则提出了关键资源的概念,虽然研究的是单技能项目调度问题,但是其有关关键资源(principal resource)、附属资源(dependent resource)和独立资源(independent resource)的阐述,能为MSPSP 的研究提供较有价值的参考.
技能水平(skill level)约束是MSPSP 研究中最常见的一种技能类约束, 在传统MSPSP 中资源对技能的熟练度是二元的, 资源对技能或是完全掌握或是完全不掌握[32], 即RFkl ∈{0,1}. 而在考虑技能水平的MSPSP 中,资源对技能的熟练水平是多元的[50],不同资源对同一技能的熟练程度存在差异,技能水平有高有低. 引入索引参数g ∈{1,2,...,G}表示资源对技能的掌握水平,以及二元参数

其中当g <g′, RFklg′= 1时,有RFklg= 1,即当资源具备高等级技能时,也必然能具备该技能的低等级技能[72].
资源技能水平的差异给项目带来的影响是多方面的,学者们从不同视角对这一问题进行了研究,其中最常见的假设是,活动会对资源的技能水平有要求[72];活动工期的长短会受资源技能水平的影响[67]等. 此外,也有部分学者假设资源的技能水平会影响项目产品的质量[49]、项目的完工率、返工率[58]以及活动对资源的需求量[50]等.
在多技能人力资源项目的研究中,员工技能存在学习效应的现象也引起了学者的关注,学习效应指的是员工的技能熟练度会随技能的使用而逐渐提高[39]. 与之相应的,还有遗忘效应:频繁使用技能会提升技能熟练度,而长时间闲置技能则会降低技能水平[76]. 表3 列出MSPSPc 的约束条件.

表3 MSPSP 的约束条件Table 3 Constraints in MSPSP
3 基于MSPSP 求解的研究综述
MSPSP 属于NP-hard 问题,具有较高的求解难度,目前关于MSPSP 的求解方法可分为三种: 精确求解法、启发式算法和元启发式算法.
3.1 精确算法
在前文所介绍的两种MSPSP 模型中,以时间为索引所构建的是0-1 规划模型,其决策变量均为二元变量,活动的开始时间Si被限定为整数,但是该模型是非线性的,虽然在求解小规模问题时便于使用穷举法等精确方法,但在大规模算例中求解则较为困难.如文献[42]以多技能资源均衡为目标,构建了以时间为索引的0-1 规划模型,利用LINGO 求解,但所求解的算例是仅包含5 个活动的项目.
引入活动时序关系后, 则可以将Si扩展为全体实数, 且该问题可被描述为混合整数线性规划模型(mixed integer linear programming,MILP),便于使用分支定界法进行精确求解. 如文献[4]建立了MILP,通过启发式算法求得解的下界后,根据活动的最早–最晚开始时间缩小了决策变量Si的取值范围,并基于活动时序关系构造了若干约束,进一步压缩了解空间. 尽管如此,现有的求解器如CPLEX 和LINGO 等,在求解MSPSP 时依旧只能处理小规模的项目案例,如文献[20]使用的案例仅包含20 个活动.
分支定界法是在精确求解MSPSP 的主要方法,而提高其求解效率的关键在于下界的计算,一个紧的下界能大大降低搜索空间,提高求解效率.目前MSPSP 研究领域求解下界的方法有两种,第一种最直观最常见的方法可称为“直接法”,也即是对模型中的某些约束进行松弛甚至直接删除,如文献[4]删除了所有资源约束,直接以关键路径的长度作为下界,文献[20]则放宽了资源约束,假设每个活动都能以最短工期进行,这种下界计算方式尽管简单,但是给出的往往是一个过于宽松的下界,紧密性较差,难以显著降低搜索节点的数量.
第二种是“突破法”[78],即先预设一个较宽松的下界,在证明该下界无可行解后,逐渐提升下界,直至出现可行解,固定下界的值.相较于直接法,突破法能有效提升下界的紧密性,但其难点也是重点,在于如何证明一个给定的下界无可行解存在,尤其由于MSPSP 中的复杂性,一旦开发出高效的证明方式,突破法获得的下界很可能远优于关键路径长度,有效减小搜索空间. 如文献[16]提出了基于“活动相容集”的下界突破证明方法,能有效求解包含32 个活动的项目算例.
3.2 启发式算法
启发式算法是一种针对具体问题开发的, 贴合问题特征的求解策略,它不保证给出问题的最优解, 但是能在可接受的时间及空间内给出可行解. 除了精确求解法以外, 大多数的项目调度求解方法都是一个不断为活动安排时间、分配资源的迭代过程,因此涉及两个问题:如何迭代,以及每次迭代内如何操作,关于MSPSP 的启发式算法也大多是围绕这两点设计的.
调度计划生成机制解决的便是如何迭代的问题, 常用的有并行调度(parallel scheduling generation scheme,PSGS)和串行调度(serial scheduling generation scheme,SSGS)两种. 算法1 和算法2 展示了两种调度计划生成机制的伪代码.

可以看出,并行调度随时间迭代,在每次迭代内不断选择满足约束的活动加入当前开始活动集,串行调度随活动迭代,在每次迭代内选择活动并按最早可开始时间为之排程. PSGS 和SSGS 之中并不存在一个普适的最优的方法,学者们根据所设计的算法采用了不同的计划生成机制,如文献[32,33]采用的是PSGS,而文献[78]则选择SSGS.
活动相容性判断在很多MSPSP 启发式算法中是很重要的一步[4],它是指根据工序约束和资源约束判断当前可同时开始的活动集合.在传统的单技能资源受限项目调度中,若干活动能否相容,除了判断工序约束外,只需对资源的供应和需求数量做简单对比即可.但在多技能项目中,由于资源具备多技能,即便资源数量是确定的,其技能分配也是可变的,简单的数量对比并不足以作为判断的依据. 而最大程度上使相容的活动同时开始,不仅能提高资源的利用率,还能缩短项目工期.如文献[32]的最小费用最大流法,文献[33]的二分图最大匹配法,都是用来求解固定资源数量下的最大相容活动集的. 对SGSS 而言,由于其每次迭代仅考虑单独一个活动,并不存在活动相容性判断的问题.这降低了问题的求解难度,但同时也会使一些原本可以并行的活动,由于资源技能的分配不合理而无法并行,导致项目工期变长,这也是更多MSPSP 启发式算法选择PSGS 而不是SGSS 的原因.
在确定了调度计划生成机制以后,需要决定每次迭代内如何操作,即图2 中的决策(Ⅰ)和决策(Ⅱ),它们分别代表活动调度以及资源指派问题.现有文献中,最常见的决策方式是通过一定的规则赋予活动和资源优先权,而后根据各自的优先权,按照一定的调度计划生成机制对项目实施调度,这类调度算法被称为基于优先规则的启发式算法. 如文献[32]考虑了活动的最迟开始时间及后续活动时间等因素以赋予活动权值,考虑了资源稀缺度技能需求度等因素以赋予资源权值,文献[33]则更进一步,在调度过程中根据资源的供给及活动的需求,动态调整资源的权值.
基于优先规则的启发式算法具有规则易理解、易设计、求解速度快等优点,尤其对于规模较大的复杂项目而言,往往能在很短的时间内求得满意解,这是精确求解法和其它元启发式算法难以企及的. 然而由于相关规则的设计具有很强的目标针对性,这使其难以被应用于求解多目标问题.如活动规则中的“具有最多后续的活动优先开始”这一规则,显然是针对优化项目工期这一目标设计的,在求解以资源、成本为目标的问题时,就很难起到作用. 此外,规则的制定还应考虑项目特征,即便对于同一类型的项目,由于活动数量、网络复杂度、资源需求强度等的不同,其最优的规则也往往是不同的,这无疑对项目计划的制定者提出了较高的知识及经验要求.
3.3 元启发式算法
相对于启发式算法而言,元启发式算法不依赖于具体问题,而是借助于一系列通用求解策略对问题进行求解,因此在MSPSP 的现有研究成果中,元启发式算法的应用最为广泛.
尽管目前有很多求解MSPSP 的元启发式算法,但其最根本的思路大多遵循着算法1 和算法2 的调度过程,即通过迭代,逐步完成对活动的调度和资源的指派. 基于规则的启发式算法是通过经验或推理设计一定的规则赋予活动和资源优先权,元启发式算法则是以随机的方式产生初始解,而后根据目标值的反馈,经过进化不断优化解的质量. 因此,元启发式算法随机性更大,但同时也具有更广的搜索空间,而且一个有效的进化机制能保证解不断向最优解收敛,这是基于规则的启发式算法所不及的.
编解码和进化策略是元启发式算法优化求解过程的两个核心内容.在MSPSP 的元启发式算法中,编码包含活动编码和资源编码,分别对应算法1 和算法2 中的决策(Ⅰ)和决策(Ⅱ). 最常见的活动编码方式有两类,第一类为按活动顺序编码[23],其个体基因位上的数值是活动的编号,在个体上位置越靠前的活动优先权越高,见图2(a),这类编码方式的优点是活动优先级明确,基因信息在传递过程中不会失真,缺点是在进行交叉变异等进化操作时,可能会产生大量需要修正的不可行解;第二类是按活动权值编码[25],其个体基因位上的数值指的是对应活动的权值,权值越大的活动优先权越高,见图2(b),这类编码方式的优点是不会产生不可行解,但是在进化时,由于不同权值在不同序列内的排序可能不同,从而导致基因交换后信息失真.
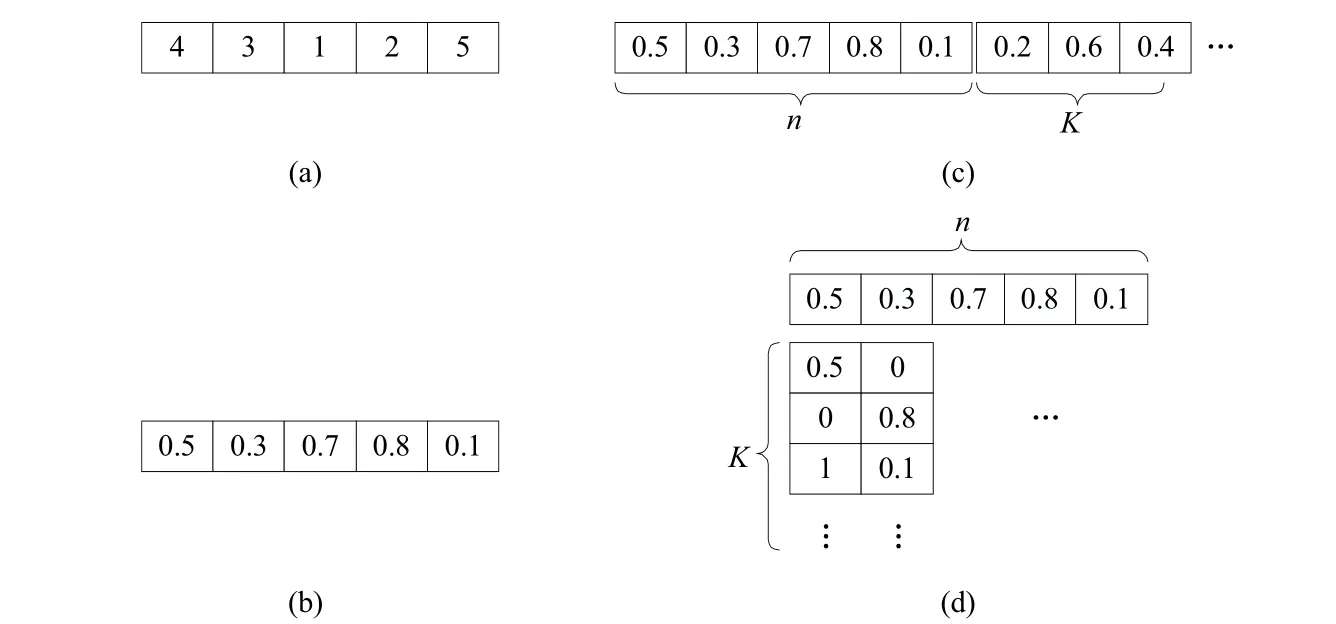
图2 MSPSP 元启发式算法常用编码方式Fig.3 Common solution representations in meta-heuristic algorithms for MSPSP
除此之外,也有文献采用了活动时间编码的方式,也即每个基因位上的数值代表对应活动的开始时间.尽管这类编码在解码时可直接生成调度计划,不需要通过调度计划生成机制处理编码信息,但是它在进化时也可能会生成大量的不可行解,且相对于按活动顺序编码,它更不易修正,因此只有针对特定的算例时,才有部分学者采用了这种编码方式[84].
部分元启发式算法中仅考虑活动,而不含资源信息,资源的指派是通过其它方式求解的,这种算法可理解为用元启发式求解决策(Ⅰ),而用启发式求解决策(Ⅱ). 在同时包含活动和资源信息的元启发式算法中,资源的编码方式也有两类,第一类是一维赋值型编码[25],即在活动编码后端继续设置等于资源数量的基因位,每个基因位上的数值代表对应资源的优先权,从而为决策(Ⅱ)的进行提供依据,见图2(c). 因此,该类编码个体结构简单易于进化操作,但由于其活动信息和资源信息是相互独立的,这就导致在进化过程会各自独立变化,不能改善活动与资源之间的匹配关系;第二类是二维赋值型编码[73],即在活动编码的下方继续编码,为对应活动赋予资源,从而使编码由一维转变为二维,见图2(d),这类编码能保证优秀的活动-资源匹配信息得到遗传,但是在进化过程可能会导致不可行解的产生,且编码复杂度会随着项目规模的增大而快速上升,算法运行时间也随之增加.
解码是将个体信息转译成具体调度计划的过程,解码过程可以说是调度计划的生成过程,由于大多数元启发式算法中个体所包含的信息仅仅是活动及资源的优先权,因此在解码时仍需要选择调度计划生成机制.对于按照活动顺序编码的算法而言,最适合的是SGSS,因为个体中的活动序列已经决定了迭代的次序,不需要额外的数据处理. 无论是哪种调度计划生成机制,两种编码方式下的个体经过处理后都可应用,更进一步地,文献[25]直接将其纳入个体的编码,在解码的过程中,只需读取个体中该基因位上的信息,采取相应的调度计划生成机制即可.这样的处理方式增大了算法的搜索空间,但是在面对具有不同特征的算例时,也能挑选出最适合的调度计划生成机制,规避了用单一调度计划生成机制处理所有项目算例的缺陷.
一般的基于规则的启发式算法难以应对多目标问题,因此在面对多目标MSPSP 时,更多的是采用元启发式算法. 在多目标求解算法中,如何根据个体目标值判别解的优劣是保证进化的关键,其中最常见的个体优劣判别方法是非支配排序技术, 它基于Pareto 最优理论,设计了拥挤度等指标,通过多目标值的对比及个体在解空间内的位置对个体排序,从而为进化提供依据. 如非支配排序遗传算法(non-dominated sorting genetic algorithms,NSGA-Ⅱ)等,具体文献见表4.
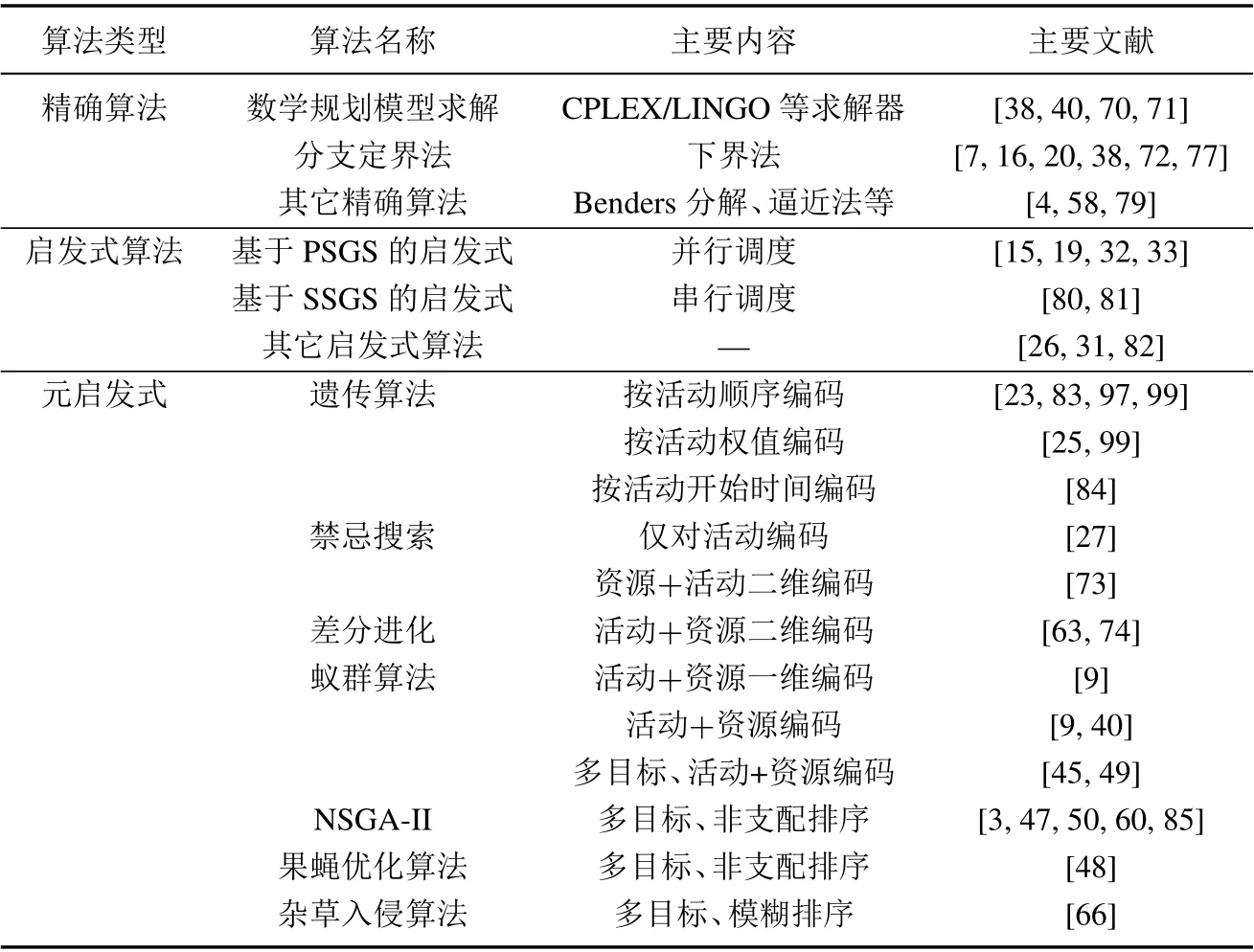
表4 MSPSP 的求解算法Table 4 Algorithms for MSPSP
3.4 算例库
在检验算法的优劣时,一个合理的数据库至关重要.MSPSP 与传统的单技能RCPSP 有共同点也有不同点,相较于传统RCPCP,MSPSP 增加了有关技能的参数,所以RCPSP 研究中所使用的标准算例库无法被直接应用于MSPSP 研究之中. 因此,有些学者在研究过程中通过修改RCPSP 标准算例库以适应MSPSP,有些学者则构造了全新的MSPSP 算例库.
算法有效性及稳健性的检验, 需要用到各种规模各种类型的项目算例, 因此项目算例库的多样化程度越高, 越具有使用价值. 一般来说, 主要从以下四个指标衡量MSPSP 算例的类型: 活动数量(number of activities, N)、网络复杂度(network complexity, NC)、资源强度(resource strength, RS)和技能因素(skill factor,SF).
文献[93]构造的项目调度算例库(project scheduling problem library,PSPLIB1http://www.om–db.wi.tum.de/psplib/main.html)是项目调度领域最常用的一个算例库. 该算例库经过不断更新,目前不仅包含普通的RCPSP 算例,还含有多模式RCPSP 算例,项目规模从小到大依次包含30,60,90 和120 个活动,且每个规模下包含480 个算例.
然而PSPLIB 中的资源均为单技能资源,它无法被直接用于MSPSP 研究.因此学者们对其做了修改,大多是在保持项目网络不变的前提下,对资源的技能、活动的需求等方面进行调整. 如文献[36]提出了一种基于PSPLIB 的多技能项目算例生成机制,构造了PSPMSWC 算例库,依据项目网络中活动数量分为四个子集: J30,J60,J90 和J120,每个子集包含360 个活动,共1 440 个项目算例.
也有学者根据MSPSP 的特点,构造全新的算例库,如文献[87]构造了专门应用于MSPSP 的iMOPSE 算例库2http://imopse.ii.pwr.edu.pl/index.html,依据项目网络中活动数量分为四个子集: J10,J15,J100 和J200,分别含有3 个,3 个,18 个和18 个算例,共42 个算例. 此外还有学者通过RanGen 软件3https://www.projectmanagement.ugent.be/生成算例,或者自行设计算例,或者直接选取现实项目案例进行研究,各文献所采用的算例库具体见表5.
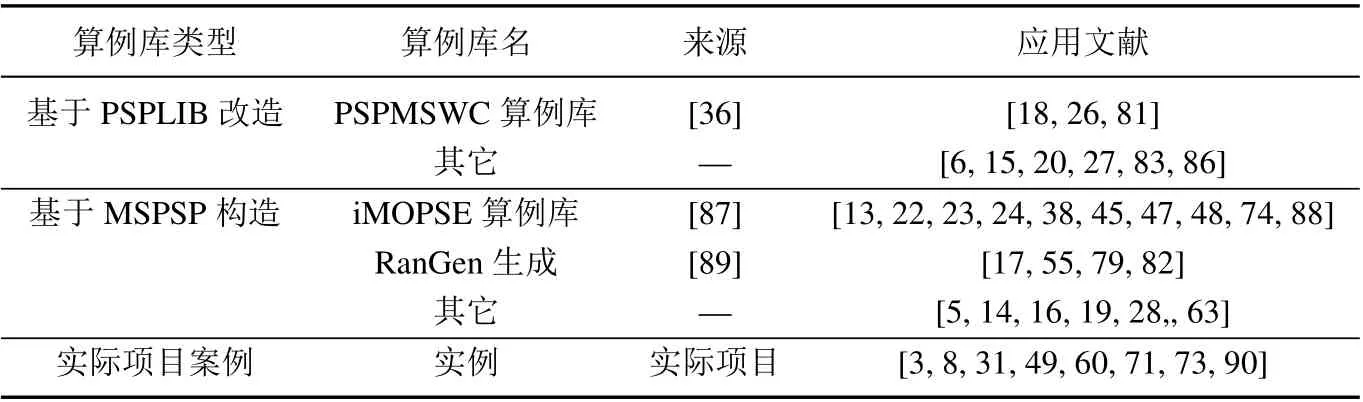
表5 MSPSP 的算例库Table 5 Case library for MSPSP
4 结束语
为给多技能项目调度的研究提供参考,本文从问题建模和问题求解两个方面分析了MSPSP 的现有研究成果.在模型的目标函数方面,目前的研究集中于优化项目的工期、成本、资源均衡等,而项目管理者所重视的目标中仍有部分鲜有学者关注,如项目净现值问题.除此之外,实际项目中管理者的目标往往更加复杂,同时考虑多个目标的调度方法更能符合现实需求. 在模型的约束条件方面,学者们将多技能与多项目、多模式、活动可中断、技能可变等方面结合,形成了较为丰富的理论成果.然而,实际项目往往具有鲜明的行业特征,所涉及的多技能资源也具有不同的特性,此外,不确定环境下多技能项目、项目组合中的多技能项目等也各具特点,所以多技能项目调度的研究,可更多地结合行业特点及项目环境,根据实际构建模型. 在问题求解方面,学者们开发了大量的元启发式算法,而对启发式算法的研究则相对较少. 但在实践中,一些基于规则的启发式算法往往更便于应用,也能给予项目管理者更多启示. 因此,如何开发出求解速度快、求解质量高的启发式方法也是未来的一个研究方向.最后,在研究所采用的算例库方面,目前所使用的大规模算例库大多是对PSPLIB 修改得来的,很难有统一的对比基准(benchmark),开发一个算例数量多的包含对比基准的大规模算例库也是MSPSP 研究的一个重点.

