共享平台下基于阈值的占线任务分配策略
代文强, 章潇月, 姜玉琦
(电子科技大学经济与管理学院,四川成都 611731)
1 引 言
随着互联网时代的来临,信息技术不断加强,共享经济作为一种新型的经济模式越来越受到人们的关注. 根据中国国家信息中心颁布的《中国共享经济发展年度报告(2020)》,2019 年我国的共享经济交易规模达到32 828 亿元,与2018 年相比增长了11.6%,并且预计至2022 年,我国共享经济的年均增幅将会继续维持在15%左右[1]. 共享经济是用户在不拥有资源的情况下访问和共享他人资源,从而提高资源利用率的新型商业模式,其本质是以获得一定报酬为主要目的,基于陌生人且存在物品使用权的暂时转移[2]. 在这其中,共享平台作为连接资源需求方与供应方的桥梁,起着基础性的作用. 目前研究共享经济的文献中,只有较少一部分从共享平台企业运营角度开展研究,已有的研究也大多都是进行定性研究,缺乏对平台的定量化研究[3]. 并且共享平台上的需求任务到达信息相当复杂,使得平台定量化研究更加困难.因此本文主要聚焦平台的定量化研究,从平台的角度出发,研究如何将需求进行实时合理分配给现有的资源以使得平台收益达到最优.
在现有针对共享平台的定量研究中,大多数是将其转化为设施规划问题.例如,以共享车辆平台为例,He 等[4]研究了单向电动汽车共享系统服务区域设计的战略规划问题,制定了一个综合服务区规划模型,考虑了用户在采用服务时的满意行为以及单向电动汽车共享系统的各种运行特性. Shu 等[5]提出了具有比例限制的网络流模型用以描述网络内自行车的周期性流动,并由此建模并分析了共享自行车的布局与再分配优化问题.Mak 等[6]提出了鲁棒优化模型用以研究并求解共享电动车公司电池交换基础设施优化选址问题.除共享车辆平台外,最近王海燕等[7]研究了医联体信息共享过程中平台运营商的最优收费定价策略以及三级医院、社区医院的参与决策和付费方式选择策略.可以看出已有的文献大多研究需求模式已知的条件下的路径规划问题或者平台定价问题.而本文研究的是在需求未知的情况下,平台方如何实时对需求进行分配以满足利润最大化的问题.
共享平台的一个典型特征是未来需求到达信息往往呈现高度不确定性. 以往针对信息不确定的建模,常用的建模思路是假设随机分布或随机过程的条件下寻求平均意义上的最优解. 但是,网络平台上的需求任务信息变化复杂,决策者往往并不能假设未来需求服从某种随机分布或随机过程. 以往文献假设的某种随机分布或随机过程的条件一旦发生变化,其给出的最优方案就会失去最优性. 近年来受到管理学界广泛关注的占线(online)问题和竞争策略(competitive strategy)的方法能够很好地处理动态特征较强的问题,其针对变化因素的每一个特例都能给出一个方案,并使得这一方案所给出的平台收益离决策者在已知该特例输入下的最优方案得到的平台收益总在一定的比例之内,因此能够避免传统的静态优化方法所得到的结论对初始假设依赖强的弊端[8-14].
就理论上来说,可以将本文研究的问题视作无任务优先权的占线区间排序问题.在以往研究占线区间排序问题的文献中,大多都考虑任务具有优先权[15]. 但在共享经济背景下,往往不能假设任务优先权的存在.已有一些学者研究了无任务优先权的占线区间排序问题,例如Boyar 等[16]在火车票保留背景下研究了占线区间排序问题,因此其可行集是若干离散集合,Gupta 等[17]研究了运输行业中的占线区间排序问题,设计了相应的分配策略.关于区间排序的综述性文献和进一步的研究,可以参考文献[18,19].
同以往的研究相比,本文的贡献在于不仅考虑了共享平台供应方服务时长的差异性,并且结合实际,考虑平台的收益规则包含每单固定价格和单位可变价格,建立了共享平台下实时占线任务分配模型,在满足不确定需求的条件下尽可能最大化平台收益.为了尽可能地让服务器服务具有较长持续时间的需求,引入阈值参数的概念,在此基础上给出了占线任务分配策略并证明了竞争性能比.本文不假设需求具有任何分布信息,因此可以弥补以往相关研究假设性太强的缺陷,同时本文也是现有占线问题研究的有益补充,具有重要的理论意义和实践价值.
2 占线任务分配模型
2.1 模型描述
首先针对共享平台下服务器及任务需求的概念进行简要的描述. 共享平台下某时刻可同时使用的资源数量称为服务器,记n代表该时刻可同时使用的服务器数量,每个服务器i的可持续服务时间被限制在一定值内,且每个服务器一次只能处理单个需求任务.以L表示需求任务的有限非空序列,需求一个个到达,对于某需求j,其开始时间用tj表示,需求持续时间长度为dj. 设最小可能需求时间长度为Dmin>0,最大可能长度为Dmax<+∞. 注意当需求j到达时,决策者只能观察到dj及之前的需求信息,dj之后的需求信息不可观察且无法预测. 记D=[Dmin,Dmax],并设需求L的集合为L(D),同时定义Δ=Dmax/Dmin.
当需求j到达时,平台的决策者必须在不知道未来需求信息的情况下立即做出决策,根据系统中存在的可服务的服务器决定将该需求分配给哪台服务器. 决策一旦做出便立即执行,且无法更改.此外,若需求k和需求l同时满足tk≤tl和tk+dk >tl,则称需求k和需求l是重叠或冲突的,显然其不能分配给同一个服务器. 令s为每单需求为平台带来的固定收益,单位可变收益设为1,其中比例为p(0<p <1)的部分是平台的收益抽成.因此,平台的收益可以表示为π=sm+pm∑i=1di,其中m为已接受需求的数量. 此外,为计算方便定义f=s/Dmin. 由于p是一个固定的常数,为便于描述,通过对收益函数的适当处理可将其等价地转化为p=1.

2.2 竞争性能比
为了证明研究问题的竞争性能比,首先提出以下定义.
定义1 给定两个集合B和C,定义集合B到集合C的分配方案ω:B×C →R+满足


对于共享平台下的任务分配问题,只要针对不同的问题特征设计相应的占线策略,再构造满足式(1)的分配方案,即可根据定理1 得到相应的竞争比. 在下面的分析中,将利用定义1 与定理1 证明本文设计的策略具有较好的竞争性能比.
3 任务分配策略及竞争性能分析
3.1 任务分配策略
本文是从共享平台的角度出发考虑如何分配任务需求使得平台收益最大化. 由于在一定条件下,需求的持续时间越长,给共享平台带来的收益越大,故引入阈值的概念尽可能的让服务器服务较长持续时间的需求. 首先给出如下阈值的定义.
定义2 每个服务器i存在一个可接受服务时间的最低值ϕ(i)(即阈值),当需求j的持续时间dj大于等于ϕ(i)时,需求j对于服务器i来说才是可指派的.
基于上述阈值的概念,一个简单的占线任务分配策略A 可以设计为如下步骤:
在丰富多彩的数学教学活动中,如果教师能把进行法制教育的方法、时机掌握恰当,运用灵活,对提高学生的思想觉悟、抵制心灵污染,定会收到良好的效果。数学教材中蕴含着极其丰富的育人因素,其中“综合与实践”板块,既能帮助学生回顾某一单元的知识网络,又能综合检测学生的实践能力,同时我们也可结合切入点对学生渗透法治教育。例如,在教学“绘制校园平面图”时,学生通过测量、计算,最终绘制出校园平面图,不仅掌握了相关知识,提高了动手能力,还可渗透《中华人民共和国地图条例法》。在教学年月日,让学生绘制年历表时,对学生渗透《全国年节及纪念日放假办法》、《中华人民共和国劳动法》。
步骤1 按照服务器的可持续工作时间对当前系统中存在的可用服务器进行排序,并按照可持续工作时间从短到长的顺序分别编号为1,2,...,n,当用户需求信息到达时,按照编号顺序将其分配给服务器,注意需求与服务器一一对应,不能重叠或冲突.
步骤2 分配给需求j的服务器i必须满足不等式dj≥ϕ(i),即需求的持续时间必须超过所分配服务器的阈值,否则就释放该需求,需求重新进入需求序列并重复进行步骤1 和步骤2,直到策略推荐出合适的服务器.
在上述策略中,核心是阈值的设计.根据以下定义计算阈值ϕ(i).
定义3 令服务器i的阈值为ϕ(i),则ϕ(i)的计算方式如下
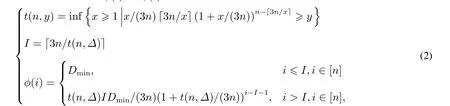
其中t(n,y)和I为中间计算式. 上述ϕ(i)的定义中以服务器的数量n和Δ作为参数输入,后续的推导也将根据n和Δ的取值分情形讨论.为了后面分析竞争性比方便,首先给出以下的结构性质.
引理1 给定一个需求序列L,令根据策略A 所确定的需求集合为BL,离线最优方案所确定的需求集合为CL,那么有以下三个论述:
1)若n=1,∀b ∈BL∩CL,每个需求任务b除了自身,不会和集合CL重叠.同样的,∀c ∈CL∩BL,每个需求任务c除了自身,不会和集合BL相重叠.
3)如果Dmax>Dmin,∀b ∈BL,与BL重叠的CL的总区间长度(服务时间)严格小于n(2Dmax+db).
证明 1)此时集合BL和CL均不包含重叠需求,因此论述1 成立. 对于2)若需求序列L已知,则集合CL里的需求也为已知,假设集合CL可以被划分为n个子集,而且每个子集只包含不重叠的需求. 在该情形下,因为所有需求任务的长度都相等,则集合BL中的每个需求任务最多与集合CL每个子集中的2 个需求任务相重叠.即BL最多和CL中的2n个需求相重叠.3)同理,假设集合CL可以被划分为n个子集,且每个子集中的需求均不重叠.则对于任意的需求b ∈BL,与需求b重叠的CL的区间长度(服务时间)小于2Dmax+db. 因此,与需求组BL重叠的CL的总区间长度(服务时间)严格小于n(2Dmax+db). 证毕.
3.2 竞争比分析
下面首先从特殊情况出发,讨论n=1,Δ=1 时的情形.
1)策略在n=1,Δ=1 时的结论.
当n= 1,Δ= 1 时,根据定义3 并经简单化简可知对于任意的i ∈[n],都有ϕ(i) =Dmin,即服务器的阈值与需求到达序列的最小区间长度相等. 首先定义如下函数.


同样简单化简可知,对于∀i ∈[n+1]时,都有ϕ(i)=Dmin恒成立.


证明 当a=b时,代表这k+1 个需求持续时间相等,此时需求i最多与2 个需求相重叠.即k <2.此时,di=a,因此di/k≥a/2. 当a >b时,与a=b的情况相反,此时k≥3,且至少有k-2 个需求在需求i的开始时间si之后开始,并在需求i的结束时间si+di之前结束. 所以,di≥(k-2)a成立. 进一步进行分式变换得,di/k≥(k-2)a/k≥a/3. 证毕.

证明 对于由该确定性策略分配给服务器i的任何给定b ∈BL,从b到集合CL{b}中非空分配是必须有持续时间大于或等于ϕ(i)的需求,并且b属于集合BL∩CL. 集合CL是已知需求到达序列L时确定的需求集合.因此,集合CL和CL{b}可以被划分成n个子集,这每个子集只包含不相互重叠的需求.

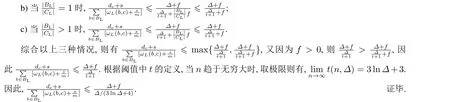
表1 汇总了以上四个定理分别给出的策略在四种不同情形下的竞争比. 综合情况1)和情况3)可知,当n ∈N,Δ= 1 时,策略的竞争比只与参数f有关,且上界为3(1+f),即策略在f取值越小时竞争比越好;综合情况2)和情况4)可知,当n ∈N,Δ >1 时,竞争比与f和Δ都相关.

表1 竞争比总结表Table 1 The summary of competitive ratios

4 数值算例
在这一节中结合数值算例评估策略的实际性能.假设有20 组需求集合在一段时间内陆续到达,相邻到达的两个集合间隔1 个单位,每组需求集合内包含x个需求任务,其中x ∈[3,10]. 每个需求的持续时间的区间为D= [6,12],系统中可服务的服务器数量为n= 5 个.假设每单需求带给平台的固定收益s= 1,可变收益为1,此时Δ=2,定义3 中的t(n,Δ)=t(5,2)≈5.405,I=3.
根据上述规则用计算机随机生成一组需求到达序列,根据本文提出的任务分配策略进行编程,得到策略A 所调度的结果如表2 和图1.

图1 A 调度结果示意图Fig.1 The scheduling results diagram of A
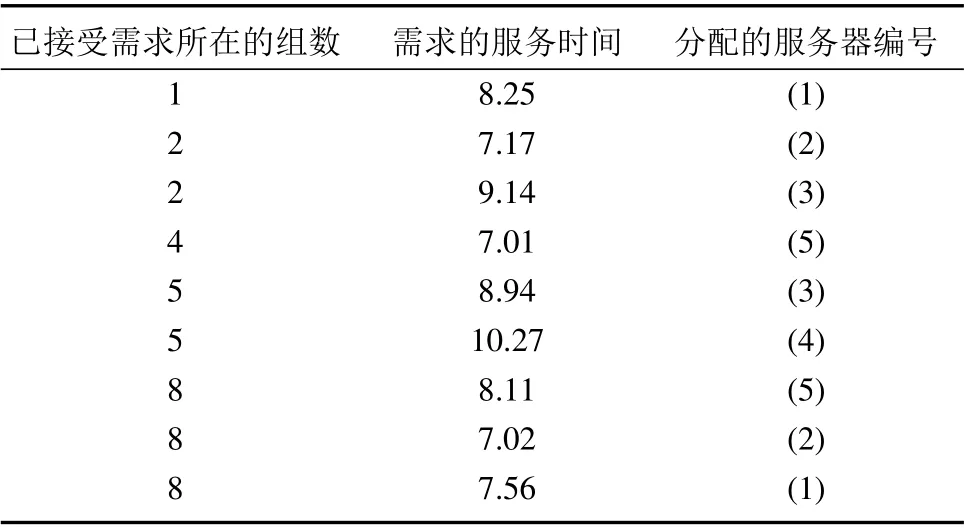
表2 A 调度结果表Table 2 The scheduling results of A

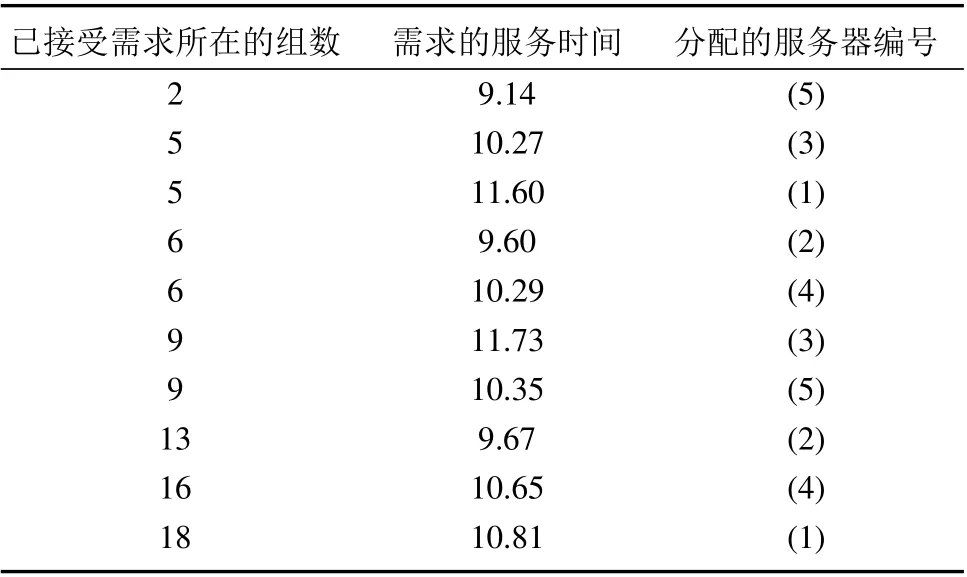
表3 OPT 调度结果表Table 3 The scheduling results of OPT
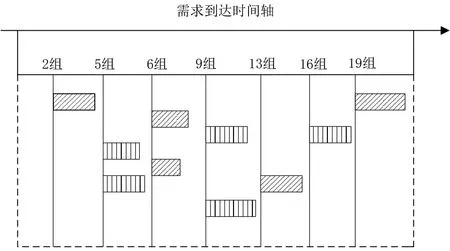
图2 OPT 调度结果示意图Fig.2 The scheduling results diagram of OPT

5 结束语
本文考虑的是共享平台下的实时任务分配问题.在实际中需求信息常常是难以预测也不可用概率分布刻画的实际背景下,考虑平台的收益包含固定收益和可变收益,建立了占线任务分配模型,引入阈值的概念,给出了相应的实时任务分配策略,从理论上证明了该策略具有较好的常数竞争性能比.在未来的研究中,可以通过考虑将更多的实际因素融入到模型中以增加模型的指导性.

