支线航运网络下集装箱分配与船舶调度联合优化
孔灵睿, 计明军, 孙以宁, 关云潇, 郭兴海
(大连海事大学交通运输工程学院,辽宁大连 116026)
1 引 言
在经济全球化的影响下,海运贸易量不断增长,集装箱运输行业在过去的数十年间呈快速、稳定的发展趋势. 2018 年,全球集装箱海运量已达到2.01 亿TEU.集装箱海运业的强劲发展,有力推动了集装箱船舶的大型化. 目前,全球最大集装箱船舶的运载能力已超过20 000 TEU.然而大型集装箱船舶在为船公司带来规模经济效益的同时,其靠港的吃水要求也决定了大型集装箱船舶只能挂靠在吃水较深的干线港. 而仅靠干线港之间的干线运输难以满足全方位的现代化运输需求,国际集装箱海运格局逐步由原来单一的港到港的运输向着干线运输和支线运输相结合的方向衍化,形成了以枢纽港(干线港)为转运中心的轴辐式航运网络. 以枢纽港口为中心的轴辐式航运网络,是海运一体化进程中出现的一种能够适应全球海运系统的网络形态[1],Msakni 等也通过实例验证了应用轴辐式航运网络的重要意义[2]. 在轴辐式航运网络中,大船通常被用来服务于各大枢纽港之间的干线运输以获得规模经济效益,小船则被用来完成支线运输任务以满足枢纽港所对应若干喂给港(支线港)的运输需求[3]. 对于轴辐式航运网络,需要明确枢纽港的位置、喂给港的挂靠方案以及枢纽港之间的班轮运输航线和服务时间表.在此基础上,如何规划最优的支线集装箱船舶调度方案,实现支线运输成本的最小化,就成为了船公司日常需要考虑的重要问题.
支线集装箱船舶运输网络同车辆路径问题(vehicle routing problem,VRP)的网络相似,均是包含一个配送中心(枢纽港)以及若干顾客点(喂给港)的二级运输网络,如图1 虚框内部分所示.
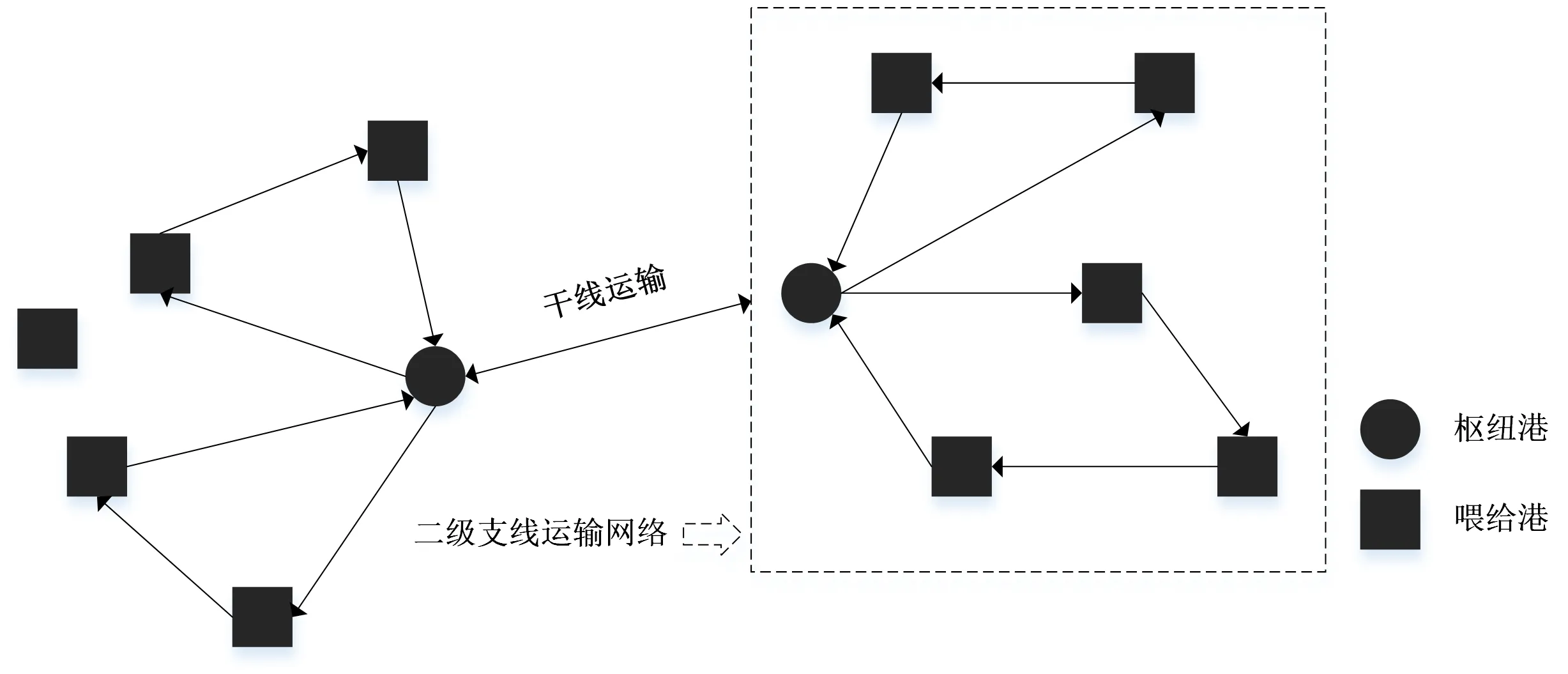
图1 二级支线运输网络Fig.1 The two-level feeder transportation network
从现代供应链和产业链的角度看, 海上集装箱运输仅是其中的一个环节, 只能满足客户的部分需求.2016 年起,以马士基集团与法国达飞轮船为首的集装箱航运巨头试图将供应链整合战略应用到海洋运输服务中. 尽管战略执行有所不同,但均以加强海洋与内陆腹地的连接、接近海洋服务终端客户为目标,以期深化企业与用户合作,打造共赢、共存和良性发展的供应链生态圈. 为顺应这一发展趋势,本文将产生集装箱运输任务的货源点加入至轴辐式航运网络的支线运输网络中,构建三级支线运输网络,如图2 所示.

图2 三级支线运输网络Fig.2 The three-level feeder transportation network
不同于传统的支线运输网络,三级支线运输网络不仅需要对支线集装箱船舶调度方案进行决策,还需同时考虑各货源点的集装箱到喂给港的分配方案.即货源点的集装箱并非提前分配至相应的喂给港,而是同支线集装箱船舶调度计划进行联合优化. 若一个货源点的集装箱通过不同的喂给港进行运输,最优的支线船舶调度方案可能会发生很大的变化,最小的运输成本也将随之改变.通过构建三级支线网络并对其进行联合优化研究,能够为航运企业向供应链终端整合提供思路,同时可以降低整体支线网络的总运输成本.
以往有关轴辐式航运网络的研究主要集中在枢纽港之间的干线运输上[4-7],有关支线船舶调度的研究较少. 关于支线船舶调度问题,Sambrocos 等[8]将其看作是车辆路径问题(VRP)的一个扩展,认为支线船舶调度是从枢纽港出发,向喂给港运货的具有容量约束的VRP;靳志宏等[9]同样将VRP 理论应用到支线集装箱船舶调度问题中,在现有研究的基础上,加入对船舶容量约束与时间窗约束的考虑,构建了混合整数优化模型,并采用粒子群算法进行求解;Karlafti 等[10]考虑了更多的实际情况,研究了喂给港既有卸箱需求也有装箱需求的情况下,枢纽港与众多喂给港之间的支线集装箱船舶调度问题,并采用混合遗传算法进行求解;为探究船型的选择对于支线集装箱船舶运输成本的影响,Ji 等[11]构建了多船型的支线集装箱船舶调度优化模型,并设计改进遗传算法进行求解;考虑船舶航速对于支线船舶调度方案的影响,Santini[12]等,计明军等[13]研究了可变航速下的支线船舶调度问题.然而,以往的研究均是基于二级支线网络,假定各喂给港的装箱量已知,即各个货源点的集装箱已提前分配至相应的喂给港,再对支线集装箱船舶调度方案进行优化. 缺乏对于供应链终端的货源点的考虑,因此难以适应航运企业向供应链终端进行整合的发展趋势,也无法使整体支线运输网络的总成本达到最小.
而对于车辆路径问题, 也有学者将其拓展为三级运输网络. 其中与本研究最为相似的是考虑需求分配的车辆路径问题(vehicle routing with demand allocation problem,VRDAP).该问题最早由Ghoniem 等[14]提出,应用于非营利性的食物配送方面,以最小化运输距离为目标建立了混合整数规划模型并设计了精确求解算法进行求解; Solak 等[15]以及Reihaneh 等[16]随后也分别设计了更优的精确求解算法对VRDAP 进行求解. 本文研究的实质可以看成是VRDAP 在支线航运网络的应用,但又与VRDAP 研究有着较大的区别:VRDAP 研究假设所有的车辆具有相同的运载能力,而本文的三级支线运输网络中包含两种运载工具,集装箱运输船舶与集装箱运输车辆,且在实际运输过程中存在着不同大小的支线集装箱船舶,因此需要对船舶不同的运载能力进行考虑;VRDAP 研究仅考虑了配送问题,而支线集装箱船舶运输既需考虑卸船需求也需考虑装船需求;VRDAP 研究没有考虑任何时间上的约束,而相比于陆路运输节点,集装箱航运港口具有更为严格的时间要求,包含喂给港的作业时间窗以及枢纽港的运输时刻表.从研究内容以及约束条件上看,本文的研究都更为复杂,更贴合支线集装箱船舶运输的实际情况.
基于上述考虑,本文将货源点加入至传统的支线运输网络中,将传统的二级支线运输网络拓展成三级支线运输网络. 针对支线集装箱船舶运输的特点,考虑船舶容量、喂给港时间窗以及枢纽港运输班期等现实因素,分析货源点集装箱在喂给港的分配与支线船舶调度计划之间的内在联系,对集装箱分配方案以及支线集装箱船舶调度计划进行联合优化,以期能够降低整个三级支线运输网络的总成本,为航运企业的升级转型提供有益借鉴.
2 问题描述与数学模型
如图3 所示,本文研究的三级支线运输网络包括一个枢纽港、挂靠在该枢纽港下的喂给港以及若干产生集装箱运输任务的货源点.通过对比图3 中的两个不同的运输方案可知,若某一货源点的集装箱被分配至另一个不同的喂给港,那么最终的支线船舶调度方案可能会发生改变,运输成本也会随之发生变化.若提前确定好货源点的集装箱到喂给港的分配,并不能够使得整个三级支线网络的总成本达到最小. 因此需要对集装箱分配以及支线船舶调度进行联合优化,以最小化三级支线网络的总运输成本.
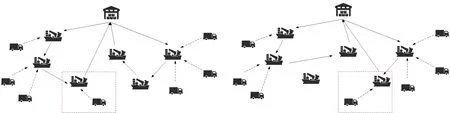
图3 货源点集装箱在不同喂给港的分配对支线船舶调度方案的影响Fig.3 The impact of the container distribution among different feeder ports on the feeder routing plan
在本文所描述的网络中,从枢纽港到每个喂给港的卸箱量已知,每个喂给港的装箱量则是分配至该喂给港的集装箱量的总和.若某一喂给港既没有卸载集装箱,也没有任何一个货源点的集装箱被分配至该喂给港,则不需要任何一艘集装箱船舶挂靠至该喂给港. 本文不但考虑船舶到达各喂给港的时间窗约束,也考虑所有货源点的集装箱必须在规定时间点之前送至枢纽港的班期约束. 此外,本文考虑多种船型的集装箱船舶,不同类型的集装箱船舶具有不同的容量、经济航速与运输费用.
本文需要解决的问题包括为每个货源点的集装箱选择装船的喂给港、为有集装箱运输需求的喂给港分配指定船舶并确定每艘船舶的运输路线,以满足运输需求、船舶容量及时间窗限制,并使得船舶运输与集装箱分配(集装箱从货源点至喂给港的运输成本)的总成本最小.
2.1 模型假设
基于支线集装箱船舶运输的特点,提出如下假设:
1)任意喂给港最多只能由一艘船舶挂靠;
2)所有的支线集装箱船舶均从枢纽港出发,完成相应的装卸任务后,最终返回枢纽港;
3)在喂给港卸下的集装箱全部来自枢纽港,且在喂给港装船的集装箱只能运输至枢纽港,即喂给港之间不存在集装箱流量;
4)所有货源点的集装箱均不能被拆分,即某一货源点的集装箱必须全部运输至同一喂给港;若同一位置的集装箱允许被运往不同的喂给港,则被视为不同的货源点;
5)在调度的过程中需要保证每一个货源点的运输需求都被满足.
2.2 模型构建
为了构建数学模型,定义如表1 所示的参数和变量.

表1 参数与变量说明Table 1 Description of parameters and variables
基于表1 中的参数以及变量定义,集装箱分配与多船型支线集装箱船舶调度联合优化模型为

其中式(1)中的目标函数表示最小化船舶运输和集装箱分配的总成本,即最小化三级支线网络的总运输成本;约束(2)定义了变量gi,若喂给港i有卸船集装箱,或至少有一个货源点被分配至喂给港i,则喂给港i有运输需求,gi= 1,否则,gi= 0;约束(3)表示每个有运输需求的喂给港有且仅有一艘集装箱船舶挂靠,若某一喂给港没有运输需求,则该喂给港没有集装箱船进行挂靠;约束(4)规定所有集装箱船舶均从枢纽港出发,其中若xkOO′=1,则表示船舶k没有被实际投入使用,是一条虚拟航线;约束(5)可以保证运输流的平衡,即驶入某一喂给港的集装箱船舶必须从该喂给港驶出;约束(6)定义了船舶从一个港口到达下一个港口的时间,保证了船舶航行的连续性,且能够消除子回路;约束(4)~约束(6)相结合可以保证每艘集装箱船舶仅分配一条运输航线,且最终均返回枢纽港;约束(7)定义了集装箱船在枢纽港进行装船作业的时间;约束(8)定义了集装箱船舶在喂给港进行装卸作业的时间;约束(9)保证船舶到达喂给港的时间满足喂给港的时间窗要求;约束(10)保证船舶返回枢纽港的时间满足船上所有集装箱必须运至枢纽港的最晚时间要求;约束(11)定义了船舶在枢纽港的装箱量;约束(12)保证喂给港的运输需求全部被满足(分配至某一喂给港的货源点的集装箱在该喂给港全部被装船);约束(13)表示船舶的容量约束;约束(14)定义喂给港的装箱量;约束(15)保证每一个货源点均被分配至一个喂给港.
假设货源点的数量为M, 包含枢纽港在内的港口的数量为N, 可以选择的船型的数量为H. 对于一个喂给港来说,其紧前喂给港有N-1 种可能,其紧后喂给港的选择也有N-1 种可能,可选的船型数量为H,那么该喂给港共可能生成H(N-1)2种方案;对于N-1 个喂给港,最多可产生H(N-1)3种方案;对于货源点的分配共可能产生M(N-1)种方案,因此问题的复杂度最终可表示为MH(N-1)4. 随着喂给港以及货源点数量的增加,使用线性求解器对模型(1)进行直接求解会消耗大量的时间,因此在本文的第3节设计了求解算法对大规模问题进行求解.
2.3 两阶段求解模型与算法
为了验证整合优化集装箱分配与支线船舶调度的优势与必要性, 在本节中介绍两阶段求解模型与算法(两阶段求解算法),用来作为第3 节中所提出的整合优化求解算法的对比基础.基于本文所研究问题的特性,可以很容易的将问题拆分成第一阶段的集装箱分配问题以及第二阶段的支线集装箱船舶调度问题.两阶段求解算法描述如下:
步骤1 集装箱分配
在第一步进行集装箱的分配,目标是最小化总分配成本. 此外,为了能够得到较好的最终解,在第一步分配集装箱时也一定程度的考虑船舶运输成本.由于此时船舶的具体行驶路径是未知的,船舶运输成本是通过计算船舶从枢纽港到各个有运输需求的喂给港的总运输成本来进行粗略的估计.因此第一阶段的目标函数可以表示为最小化集装箱分配成本与粗略估计的船舶运输成本的加权平均成本,如式(16)中的目标函数所示(在集装箱分配模型中,γ为0-1 之间的小数,表示集装箱分配成本在目标函数中所占的比重;模型中涉及到的其他符号的表示同模型(1)).
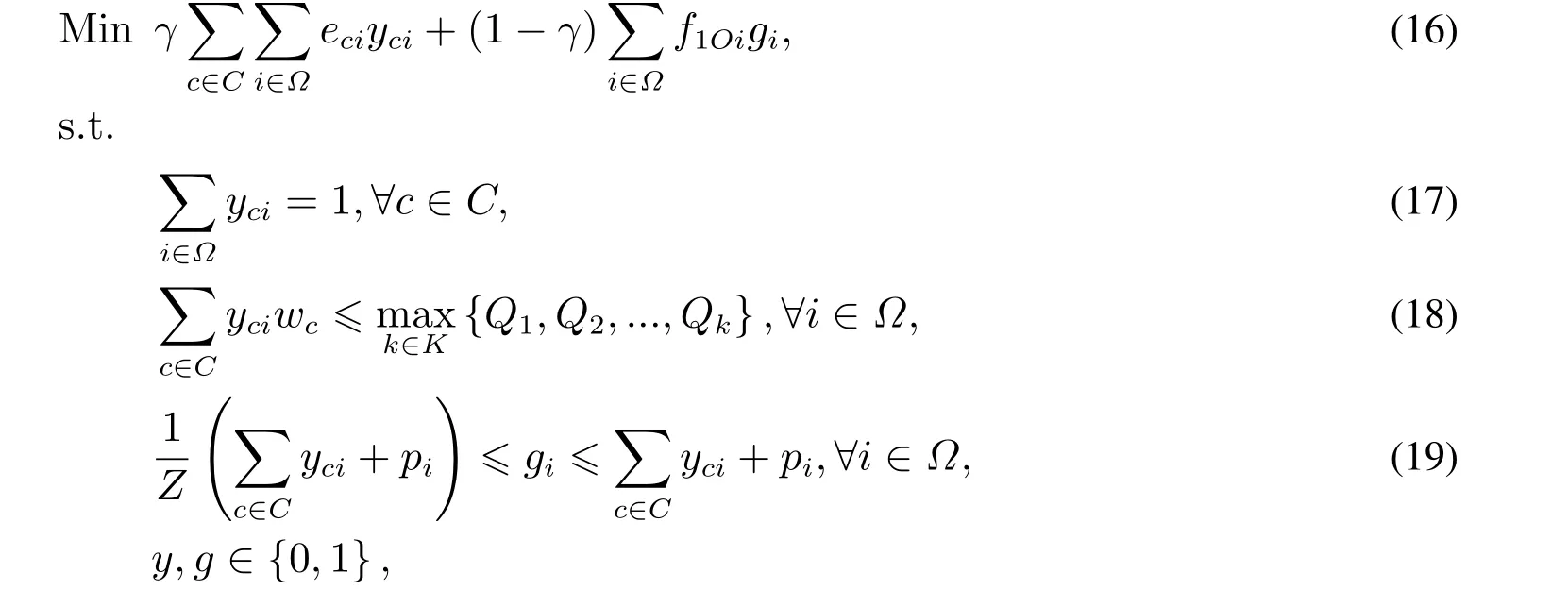
其中约束(17)保证每个货源点都被分配且仅分配至一个喂给港;约束(18)能够保证得到相应的集装箱分配方案后,在第二阶段进行船舶调度的过程中不会超过船舶的容量约束;约束(19)定义了变量gi.
该模型可直接使用线性求解器进行求解.
步骤2 支线集装箱船舶调度
当每个货源点的集装箱都被分配至相应的喂给港后,原问题就变成了已知集装箱分配以及各个喂给港运输需求的支线集装箱船舶调度问题.两阶段算法第二阶段的支线集装箱船舶调度模型与模型(1)结构相同,不同点为在支线集装箱船舶调度模型中,模型(1)中的变量gi和yci成为了已知参数,为两阶段算法中第一阶段的求解结果.关于此阶段模型的求解算法并非本文研究重点,采用以往研究中已提出的启发式算法进行求解. 由于本文考虑的是多船型下的支线集装箱船舶调度问题,因此参考文献[11]中描述的遗传算法对两阶段算法的第二阶段进行求解.
3 基于列生成的整合优化求解算法
3.1 列生成求解算法原理及框架
列生成算法是求解大规模整数规划问题的优化算法,其理论是由Danzig 等[17]提出的Dantzig-Wolfe 分解. 目前,该算法被用于对VRP 进行求解,并取得了很好的效果[18-19]. 考虑到本文所研究的问题为VRP 的一个变形与拓展,因此参考求解VRP 的列生成算法,基于本文所研究问题的特性,设计基于列生成的求解算法对问题进行求解.
应用列生成算法,首先是根据分解原理将模型(1)进行分解变型,生成与模型(1)等价的,拥有同样最优解的集分割模型. 在集分割模型中,用单一加权约束代替了多面体集约束大大减少了约束的数目,但因这个多面体的顶点可能非常多,因此增加了约束矩阵的列数. 而这种多列的问题则可以采用列生成技术进行求解.
对于集分割模型, 首先将其线性松弛并将松弛后的集分割模型称为主问题(master problem, MP)模型.若n代表MP 模型的变量数量,m表示MP 模型的约束数量,根据集分割模型的特点可知n远远大于m. 因此MP 模型的基本可行解的数量可表示为Cmn,即其可行域的顶点有Cmn个.当n很大时,即使m较小,总极点数量也十分的庞大.因此列生成算法的基本思想为:使用主问题模型所有列的部分子集构建受限主问题(restricted master problem,RMP)模型,并对RMP 模型进行求解,然后通过迭代向RMP 模型中加入能够使得RMP 模型的目标函数值继续降低的列(最小化问题),直至无法找到这样的列时,即求得MP 模型的最优解. 实际上,在线性规划的最优解里,基变量的数目永远不会超过约束数目. 因此可以不用在求解时生成全部的列,只是在需要的时候才生成新的列添入至模型当中,这样就可以使用较少的列获得MP 模型的最优解,能够大大加快求解的速度.
新加入列的原则是基于求解线性规划的单纯型法原理: 在列生成算法中,将RMP 模型中未加入的列默认为MP 模型的非基变量. 如在未加入的列中存在某一列s,其检验数小于0(最小化问题),那么列s的加入会使得RMP 模型的目标函数值进一步降低,因此需要将列s加入至RMP 模型中再次求解RMP 模型. 这个过程反复进行直至不存在检验数小于0 的列为止,则说明MP 问题已求得最优解. 由于MP 模型的列十分的多,不可能通过枚举方法来找到可加入的列,因此要构造一个子问题(sub-problem,SP)模型,来获得可加入的列并判断MP 模型的最优性. 典型的,通过这种交互方法,只需要进行有限次迭代即可获MP 模型的最优解.
在求得MP 模型的最优解后,将0-1 整数变量约束加入至当前的RMP 模型即可求得集分割模型的整数解. 本文所设计基于列生成的整合优化求解算法的具体步骤总结如下:
步骤1 构建集分割模型,并松弛其整数约束以构造MP 模型(见3.2 节);
步骤2 以两阶段算法最终求得的集装箱分配以及船舶调度方案作为列生成算法的初始可行解(即初始列);
步骤3 用初始列构建RMP 模型(一条可行的船舶路径及相应的集装箱分配方案对应着RMP 模型的一列);
步骤4 构建能为RMP 模型生成新列,且能够判断MP 模型最优性的SP 模型(见3.3 节);
步骤5 用线性求解器Gurobi 求解RMP 模型,获得当前RMP 模型的对偶变量值;
步骤6 将当前的对偶变量值代入SP 模型,求解SP 模型,如果没有可添加的列(任何未加入列的加入均无法使RMP 模型获得更小的目标函数), 则MP 模型已求得最优解, 转入步骤7. 若存在可添加的列使得RMP 模型的目标函数值能够进一步降低,则将相应列加入至RMP 模型中,转入步骤5;
步骤7 向当前的RMP 模型中加入0-1 整数变量约束,求得集分割模型的整数解.
3.2 集分割模型
集分割模型的部分参数定义如表2 所示,其余参数同模型(1).

表2 参数与变量说明Table 2 Description of parameters and variables
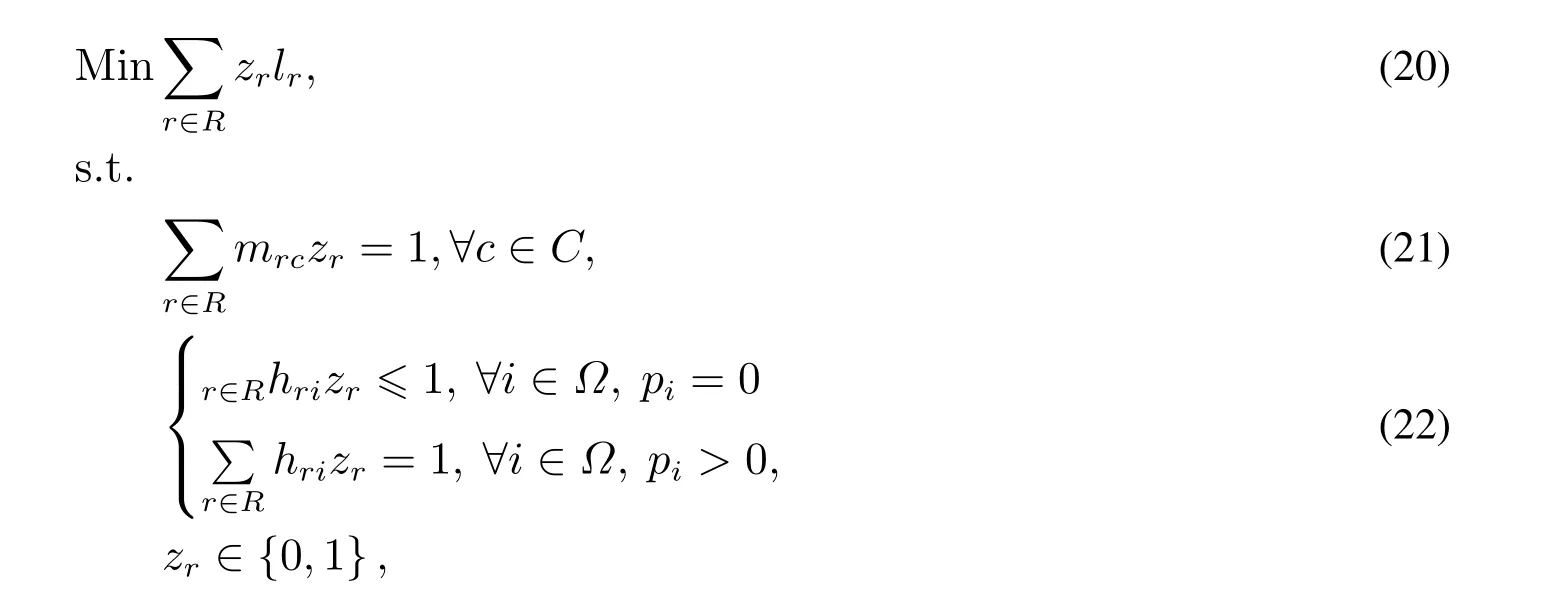
其中模型(20)的目标函数表示最小化方案的总成本,与模型(1)的目标函数等价;式(21)表示每一个货源点均被分配且仅被分配一次;式(22)表示若pi=0,则喂给港i最多被一条船舶路径访问,若pi >0,即有从枢纽港运输至喂给港i的集装箱,则该喂给港必须被访问且仅被访问一次.
至此, 模型(1)被转化为与其等价的集分割模型. 模型(1)原本有大量的约束, 而集分割模型的约束仅为|C|+|Ω|个,与模型(1)相比大为减少. 在集分割模型中,每一个列都代表着一个可行的方案.
为应用列生成算法,首先将集分割模型进行线性松弛,将zr ∈{0,1}替换为0 ≤zr≤1,并称线性松弛后的集分割模型为主问题模型(MP 模型).
3.3 子问题模型
根据单纯型法的原理,把检验数小于0 的列代入至RMP 模型中迭代,能够优化当前最优解. 因此可将最小化检验数的值作为子问题的目标函数,若子问题的目标函数值小于零,则把所求得的方案转化成列代入至RMP 模型中继续求解,若子问题的目标函数值大于等于0,则证明MP 模型已经求得了最优.
为了表示MP 模型某一列的检验数,用βc表示约束(21)所对应的对偶变量,用αi表示约束(22)所对应的对偶变量. 则MP 模型某一列的检验数可以表示为

为构建SP 模型,重新定义模型(1)中的一些参数,V表示当前所选船舶的速度,Q表示当前所选船舶的容量,fij表示当前所选船舶在i-j段的运输成本.
xij为0-1 决策变量,表示船舶是否行驶i-j段;yci的表示同模型(1);ti表示船舶到达港i的时间;si表示船舶在港i的作业时间;ui表示船舶港离开港口i时的载箱量;qi表示船舶需要在港口i装载的集装箱总量.

其中模型(25)的目标函数表示最小化检验数的值;式(38)描述了变量xij和变量yci的关系:若当前船舶路径不经过喂给港i, 则当前方案下任一货源点都不能分配至喂给港i; 式(26)~式(37)的表示可参考式(4)~式(15),此处不再赘述. 区别为SP 模型仅生成一条船舶路径及该路径下的集装箱分配方案,且不用保证每个有运输需求的喂给港都被访问,也不用保证每个货源点均被分配,只是求得一条能够使得目标函数最小的可行路径以及相应路径下的集装箱分配方案.求解SP 模型,得到变量xij和变量yci的值之后,通过转换即可到一个可行方案r,及相应的hri,mrc和lr的值.
对于SP 模型,即使集装箱被提前分配好了,该问题可看作是一个TSP 问题,用线性求解器求解中大型规模算例仍然较为困难,因此在本文的3.4 节中设计了启发式规则对SP 模型进行求解.
3.4 ALNS 算法求解子问题
子问题是具有容量和时间窗约束的基本最短路径问题的一个扩展, 可以定义在一个有向图G=(P ∪C,E ∪E′)上. 顶点集合由集合P和集合C构成,其中P是港口集合(P=Ω ∪O ∪O′),C为货源点集合;边集合包括集合E和集合E′,其中E={(i,j)|i ̸=j ∈P},E′={(c,i)|c ∈C,i ∈Ω}. 根据子问题的目标函数,属于集合E的边的费用和属于集合E′的边的费用分别为

在每次求解主问题得到新的对偶变量值之后都需要对边的费用进行更新. 对边的重新定价,可能会产生负的费用值.Feilet 等[20]运用动态规划算法对含负费用边的最短路径问题进行求解.若使用动态规划算法求解子问题,在拓展标签的过程中,设某港口有10 个可选择的货源点,其所能形成的集合为210个,那么当前港口可以拓展的标签数量最多可达210. 尽管有很多标签在拓展的过程中由于不可行或是被另一个标签统治而删去,可拓展标签的数量仍然十分多.经实验验证发现通过动态规划算法求解子问题的效率很低.因此本文设计启发式规则对子问题进行求解.
本文基于自适应大规模邻域搜索算法(adaptive large neighborhood search,ALNS)设计求解子问题的启发式规则,算法的具体描述如下:
1)初始解
定义N为港口数量,M为货源点数量,一个初始解可以表示为O,1,2,N+1,N+2,6,N+3,O′,其中O和O′分别表示枢纽港和虚拟枢纽港,1~N的数字分别表示喂给港的编号,N+1~N+M的数字分别表示第1 个到第M个货源点,即小于等于N的编号为喂给港;大于N的编号为货源点.
因此如上初始解所表示的船舶路径为O-1-2-6-O′,其中货源点1 和货源点2 被分配至喂给港2,货源点3 被分配至喂给港6.
2)邻域搜索动作
针对初始解的生成规则和问题的特性,设计了四种邻域动作:(a)随机插入—随机选择解的一个位置插入一个0~M+N之间的与原解不重复的数值.(b)最优插入—评估所有插入位置以及所有可插入的不重复的数值,选择一个最好的插入位置和相应最好的插入数值对原解进行更新. (c)随机移除—随机选择解的一个位置并移除该位置的数值.(d)最优移除—评估所有可以移除的位置,选择一个最优的移除位置并移除该位置的数值.
在进行邻域动作时需要遵循以下规则:插入的数值必须与原解中的所有数值不重复;插入或移除的位置不能是解的最左边或者解的最右边(保证船舶必须从枢纽港出发并最终返回枢纽港).
3)自适应邻域搜索规则
在算法最开始随机生成10 个初始可行解,在进行邻域搜索时,随机在10 个解中选择一个解进入邻域搜索操作.在进行邻域搜索之前,首先根据4 种邻域动作的权重值(算法初始时,四种邻域动作的权重值相同,在迭代的过程中需要根据解的好坏进行更新),运用轮盘赌机制选择一个邻域动作,再对所选定的解进行该邻域动作下的邻域搜索.当每次通过邻域搜索得到新解比当前解更优时,则用新解替代当前解;若新解比当前解差,则以一定的概率接受新解成为当前解. 设置能够使子问题目标函数值为负的解的集合为S,若新解的目标函数值小于0,则将该解加入到集合S当中,并对该解进行记录,禁止加入重复的解到集合S.
在选择邻域动作之前,还需要根据当前进行邻域搜索的解的长度对四种邻域动作当前的权重值进行临时的设置.邻域动作随机插入和最优插入的权重值依据式(41)进行临时设置;邻域动作随机移除和最优移除的权重值依据式(42)进行临时设置,即
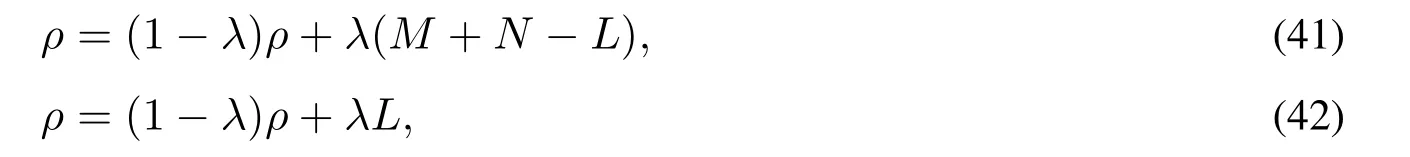
其中λ为0-1 之间的小数,M为货源点的数量,N为港口的数量,L表示当前要进行邻域搜索的解的长度.
根据式(41)和式(42)对邻域动作的权重进行临时的设置,可以使得在原有权重的基础上,长度越长的解越可能进行移除操作,长度越短的解则越可能进行插入操作.在选择完某一个邻域动作后,还需要对四种邻域动作临时设置的权重值进行还原.
此外,在完成一次邻域动作搜索后,需要依据所得新解的好坏,按照式(43)对当前所选邻域动作的权重值进行更新,即

其中µ为0-1之间的小数,φ是当前进行的邻域搜索所得结果的评估值,具体表示为

其中ω1>ω2>ω3>ω4>0
4)不同船型的处理方法
每次判断生成的新解是否可行时,均按照最大船型的参数进行计算.但在得到一个可行解后,计算其成本以及SP 模型目标函数之前,需要判断是否可以在保证解可行的形况下,更换更小的船型,若可以的话则按照当前可更换的最小船型计算相应参数的值.
5)算法停止规则
ALNS 算法迭代10 000 次停止.若集合S为非空,则将S中所有解转化成列加入到RMP 模型中. 求解RMP 模型,得到新的对偶变量值后,再进行ALNS 算法;若S为空则可看作当前MP 模型中不存在检验数为负的列,可以判断MP 模型已经求得了最优解(近优解).
ALNS 算法的步骤如下所示:
步骤1 随机生成10 个初始可行解;
步骤2 设置初始迭代次数iter←0;
步骤3 为所有的邻域动作设置相同的初始权重;
步骤4 在10 个解中随机选中一个解s;
步骤5 按照解s的长度对四种邻域动作的权重值进行临时设置;
步骤6 采用轮盘赌机制选择一个邻域动作,对解s进行该邻域动作下的邻域搜索,生成一个新解s′,并对临时设置的权重值进行还原. 若解s′优于解s,则用s′替换s,若解s′比解s差,则以一定概率接受s′;
步骤7 若解s′的目标函数值小于0,则将解s′加入至集合S中并对解s′进行记录,防止其被重复加入集合S;
步骤8 按照当前所选择的邻域动作的搜索结果,对该邻域动作的权重进行更新;
步骤9 iter←iter+1. 如果iter ≤10 000,则转至步骤4,否则转至步骤10;
步骤10 输出集合S,算法终止.
4 实验结果与分析
本文基于珠江三角洲地区,选取一个枢纽港、若干喂给港以及若干货源点构成三级支线运输网络. 设计不同规模的算例,分别运用线性求解器Gurobi、两阶段求解算法、整合优化求解算法进行求解,以验证模型的准确性、算法的求解效率以及本文的研究意义.实验的计算机参数配置为Intel(R)Core(TM)I5-8265U,1.80 GHz,8 GB RAM.算法在Visual Studio 2017 C++中实现编码,所使用的Gurobi 版本为8.1.0.
4.1 算例描述
1)设置包括枢纽港在内的港口数量|P| 为10,15,20,25,30;货源点数量|C|为10 到80 不等. 对于不同的(|P|,|C|)组合,共计生成45 个算例.
2)选取三种类型的支线集装箱船舶,分别为100 TEU,150 TEU,200 TEU.
3) 在距离枢纽港一定半径范围内随机生成指定数量的货源点, 各货源点的集装箱运输需求在10 TEU~45 TEU 之间随机生成.
4)各喂给港的卸箱量设置:0.2 的概率为0 TEU;0.8 的概率在15 TEU~55 TEU 之间随机生成.
5)各港口的效率、时间窗限制以及各货源点集装箱最晚运至枢纽港的期限在一定范围内随机生成.
4.2 实验结果与对比分析
为了更好的展示三级支线运输网络中,货源点集装箱分配对于支线船舶运输路径以及运输成本的影响,分别使用两阶段求解算法和整合优化求解算法对10 个货源点和10 个港口的算例进行求解,求解结果如表3 所示.

表3 两阶段求解算法vs.整合优化求解算法Table 3 Two-phase algorithm vs. integrated optimization algorithm
在两阶段算法的求解结果中,货源点的集装箱实现了最优分配,得到了最小的集装箱分配成本1 050 元.在最优的集装箱分配方案下,需要使用2 艘100 TEU 的集装箱船舶和1 艘150 TEU 的集装箱船舶实现最优的船舶调度,相应的支线船舶运输成本为32 450 元,最终的总运输成本为35 500 元;在整合优化求解的结果中,货源点1 被分配至喂给港5,货源点4 和货源点6 被分配至喂给港9,均没有进行最优的分配,集装箱分配成本增加至1 080 元. 然而在该集装箱分配方案下,仅需要3 艘100 TEU 的集装箱船舶即可实现支线船舶的最优调度,船舶运输成本大大降低. 整合优化算法求得的总运输成本比两阶段求解算法求得的总运输成本降低19.37%,初步验证了构建三级支线运输网络以及进行整合优化的意义.
为了进一步验证算法的有效性和本文的研究意义,分别运用3 种求解方法对45 个不同规模的算例进行求解,求解结果如表4 所示. “*”表示Gurobi 运行1 h 没有得到最优解,相应数值为Gurobi 运行1 h 得到的满意解;“—”表示Gurobi 运行1 h 没有得到可行解;Gap1 为整合优化算法求解结果与Gurobi 计算结果的对比情况;Gap2 为整合优化算法求解结果与两阶段算法求解结果的对比情况.
表4 中结果显示, 使用线性求解器Gurobi 求解模型(1)时, 只有算例1、算例2、算例3、算例10 和算例19 在1 h 内求得了最优解,其余算例均无法在1 h 内求得最优解或可行解.而对于所有的算例,整合优化求解算法均能在12 min 内求得最优解(近优解),平均求解时间为469.29 s.
此外,对Gurobi 和整合优化算法的求解结果进行对比分析可以发现,对于Gurobi 可以在1 h 内求得最优解的算例,整合优化算法的求解结果与Gurobi 的求解结果相差最多为1.78%,最少为0,平均相差0.81%;对于其他算例,整合优化算法所求的成本均小于Gurobi 求解1 h 所得到的成本.
图4 为表4 中Gap1 值的柱状图,进一步展示了除了4 个算例之外,整合优化算法的求解结果均优于或等于Gurobi 的求解结果,成本最多可降低22.47%,平均降低7.44%. 因此,通过对比Gurobi 以及整合优化算法的求解结果,验证了整合优化算法的求解效率.
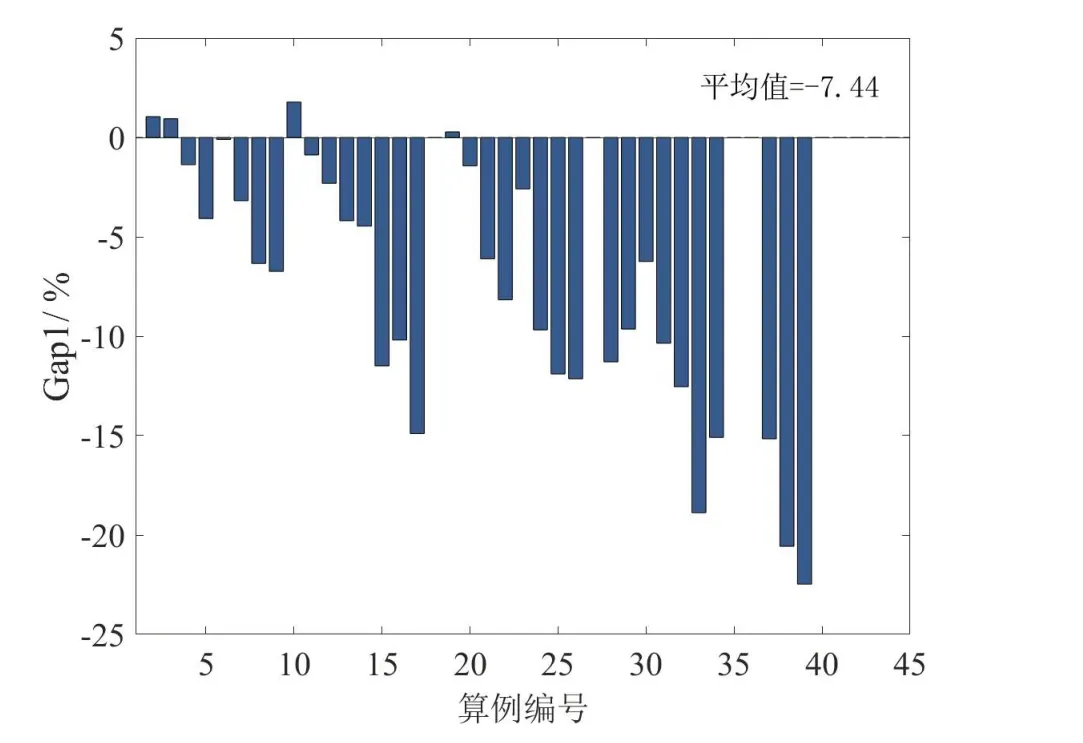
图4 Gap1 柱状图Fig.4 The bargraph of Gap1
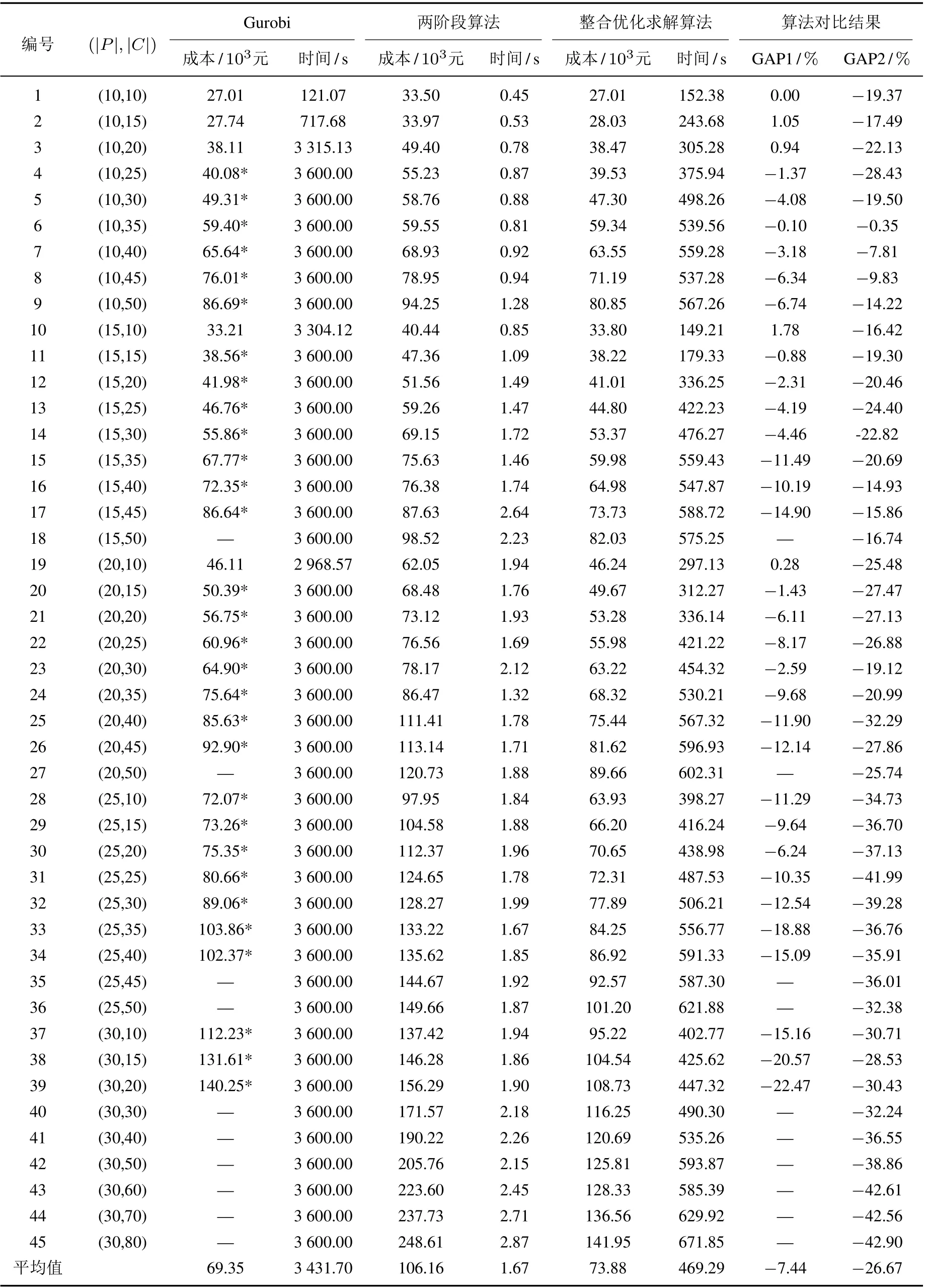
表4 三种求解方法下不同规模算例的求解结果Table.4 Computational results of three types of methods for different size of instances
此外,对比观察表4 中整合优化算法的求解结果与两阶段算法的求解结果可知,对于所有的算例,整合优化算法的求解结果均要优于两阶段算法的求解结果.在45 个算例中,既存在集装箱分配发生变化后可以将大船换成小船使总成本降低的情况,也存在集装箱分配发生变化后,集装箱船舶的行驶路线发生改变而使总成本降低的情况.
图5 为表4 中Gap2 值的柱状图,由图5 可知,整合优化集装箱分配与支线船舶调度最多可使成本降低40%以上,平均成本降低值为26.67%,充分验证了整合优化求解的必要性以及本文的研究意义.
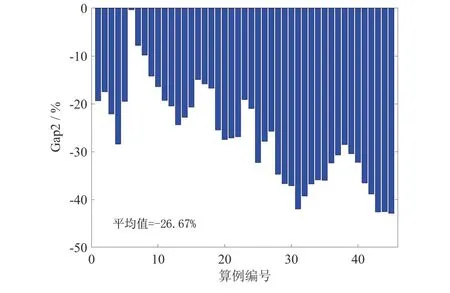
图5 Gap2 柱状图Fig.5 The bargraph of Gap2
为证明使用多船型集装箱船舶对于本文所研究问题的优势,选取表4 中算例28~36 共9 个算例,运用整合优化求解算法,分别对多船型、仅100 TEU 船型、仅150 TEU 船型、仅200 TEU 船型4 种情况进行求解,求解结果如图6 所示.
由图6 可知,对于所有算例,使用多船型的调度方案均比单一船型要好,且差别较为明显,因此验证了使用多船型集装箱船舶进行集装箱分配与支线船舶调度联合优化的必要性.
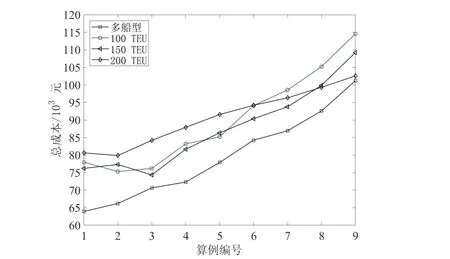
图6 多船型调度与单一船型调度成本对比Fig.6 The difference between the cost for the scheduling of single-type containership and multi-type containership
5 结束语
为顺应航运企业向供应链终端整合的发展趋势,同时考虑到货源点集装箱分配方案对于支线集装箱船舶调度成本的影响,本文将有集装箱运输需求的货源点加入传统的支线船舶运输网络进行研究,构建了三级支线运输网络. 以运输总成本最小化为目标,建立了集装箱分配与集装箱船舶调度联合优化模型,并分别采用两阶段求解算法以及基于列生成原理的整合优化算法对问题进行求解. 实验结果表明,整合优化求解算法相对于线性求解器Gurobi 更具优势,由此验证了整合优化算法的有效性;对比两阶段算法与整合优化算法的求解结果,整合优化算法能够得到更低的支线网络运输总成本,验证了整合优化的重要性.
本研究可为集装箱船舶运输企业向供应链终端延伸服务的愿望和计划提供建议,促使其与产生集装箱运输需求的客户方进行合作,提前预知运输需求,获得能够使支线运输总成本最低的集装箱分配计划与船舶调度方案,从而进一步加强航运企业同内陆腹地的连接.将集装箱运至枢纽港进行后续的干线运输有明确的时间要求,因此本文的研究主要侧重于三级支线网络的集运过程.而对于网络末端的配送问题,则具有更强的不确定性,需要考虑喂给港的堆场容量、外集卡的提箱时间、堆场的堆存成本等诸多因素.在未来的研究中,拟在此研究基础上,对三级支线网络疏运过程中的协同优化问题开展进一步讨论.

