基于启发式算法的农机混流装配线平衡分析与优化
包建军,李 明,袁逸萍
(新疆大学机械工程学院,新疆 乌鲁木齐 830047)
1 引言
随着制造业的迅速发展,我国制造业由传统的手工式生产方式向“智能制造”方向迅速发展[1]。农机生产也进入新的发展时期,现代农机生产具有小批量多品种的特点,因此在生产布局规划时不仅需要考虑装配线能否满足产能要求,更要使装配线适应现代农机生产的特点[2]。在现代制造中,装配工作量占整个产品研制工作量的(20~70)%,平均为45%,装配时间占整个制造时间的(40~60)%[3],目前农机企业装配车间在实际生产中普遍出现工位上在制品积压、工位空闲等生产不平衡现象。在此背景下,混流装配线成为了农机装配车间的主要作业方式。混流装配线一般由多个单元工位构成,各单元工位安装若干机床,并以统一的节拍生产作业[4]。农机企业需要根据自身实际情况对混流装配线进行平衡分析和优化,使混流装配线在加工时间上不产生闲置同时达到负荷均衡。
混流装配线的高效性很大的程度上取决于能否提高产线平衡率,国内外有许多学者从不同方面研究了混流装配线平衡问题。Tsai等论证了产品排产问题是一个Hard-NP问题[5]。为了解决这个问题,研究人员普遍用了算法改进、目标多样和混合型产品等方法,所采用的优化算法主要有模拟退火算法[6]、遗传算法[7]、蚁群算法[8]、粒子群算法[9]等。文献[10]在综合考虑工作节拍、优先关系约束以及其它相关约束下,用禁忌搜索算法数字化求解。
综上所述,大多数文献对再平衡的研究是在任务再分配、人员再分配以及库存约束的理论上计算平衡问题,没有对车间实际情况作出充分的数据收集和调研,所用算法在实际使用上有一定困难。这里在对某农机企业装配装配线调研的基础上,针对某玉米机不同型号产品的装配线为背景进行了实际分析,运用启发式算法对该混流装配线的平衡问题进行了构建与优化,最后对优化后的混流装配线效果进行评价,以期为农机企业混流装配线平衡优化提供有效借鉴。
2 某农机企业装配线现状分析
某农机生产车间目前装配的玉米机主要有三种型号,分别是:Y1、Y2和Y3,年订单量分别占总量的58.33%,25%,16.67%;三种不同型号的产品结构和装配流程相似,具有混流装配的特性,可通过设计混流装配线对三种产品进行混流装配。
目前车间三种型号的产品分别由三条装配线各自装配,现以Y1产品装配线为例进行装配线平衡分析,运用工业工程中的秒表法测量各工位工时结果,如表1所示。

表1 Y1产品装配线时间分析Tab.1 Time Analysis of Y1 Assembly Line
由表1可得出Y1装配线平衡分析图,如图1所示。

图1 Y1装配线平衡分析图Fig.1 Balance Analysis Diagram of Y1 Assembly Line
同样的,运用秒表法测量Y2、Y3产品各工位装配时间,得到Y2、Y3的装配线平衡分析图,如图2、图3所示。
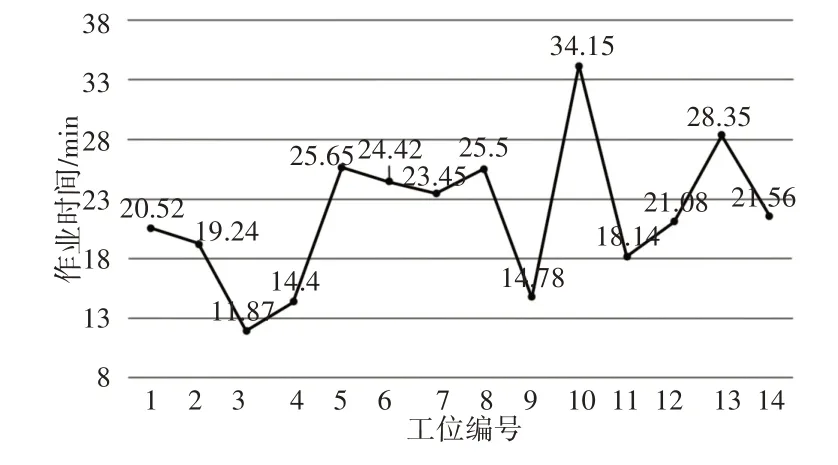
图2 Y2装配线平衡分析图Fig.2 Balance Analysis Diagram of Y2 Assembly Line

图3 Y3装配线平衡分析图Fig.3 Balance Analysis Diagram of Y3 Assembly Line
通过平衡分析可以得出:由于原Y1、Y2和Y3装配线人员分配不合理,各工位负荷不均匀,以及物料配送不及时的原因,导致装配线经常出现在制品堆积和等待,造成生产效率较低,浪费严重。汇总三条装配线分析结果,如表2所示。
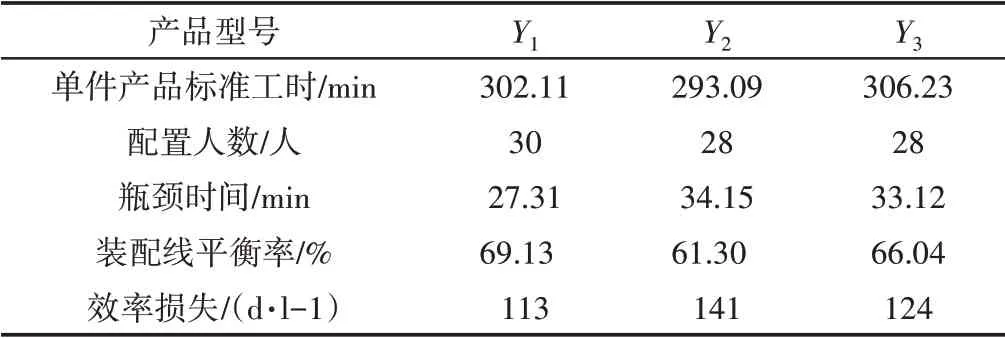
表2 Y1、Y2和Y3装配线平衡分析结果汇总Tab.2 Balance Analysis Results of Y1,Y2 and Y3
由表2可以看出,原产线生产效率较低,三条装配线平衡率都在70%以下,效率损失在113~141d之间,产线浪费严重。
3 混流装配线优化
运用启发式算法求得混流装配线的平衡优化方案,首先需要确定作业的先后顺序,得到混流装配线的作业优先顺序图,绘制混流装配线的作业优先图,首先需要收集各工位的作业时间,然后再将各个工位进行编号。
3.1 计算综合作业时间
其综合作业时间计算方式如式(1):

式中:Ti—作业优先顺序图中作业元素i的作业时间,min;Pj—产品j在总量中所占的比例,%;tj—产品j的标准作业时间,min。
根据式(1)计算三种产品构建混流装配线的综合作业时间,计算结果,如表3所示。
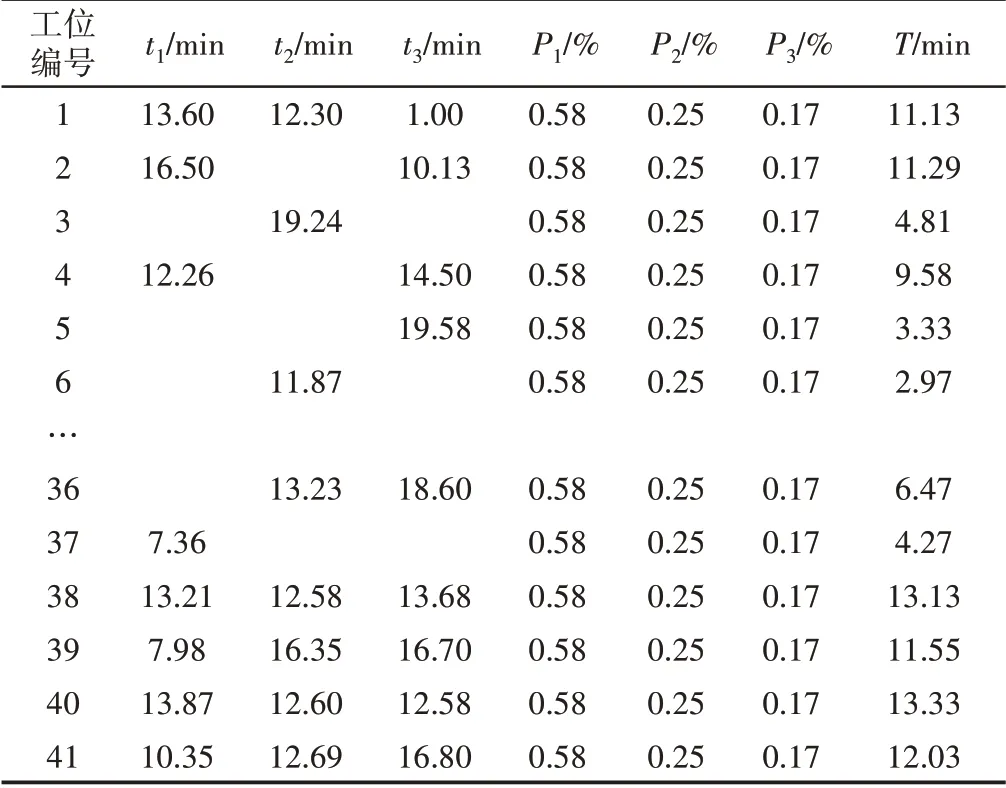
表3 Y1、Y2和Y3产品综合作业时间Tab.3 Comprehensive Operating Time of Y1,Y2 and Y3
3.2 作业优先顺序图
通过以上绘制玉米机的作业优先顺序图,如图4 所示。其中,圆圈代表作业工位,圆圈上的数字表示对应作业工位的完成时间,箭头表示整个作业完成顺序上的先后约束关系。
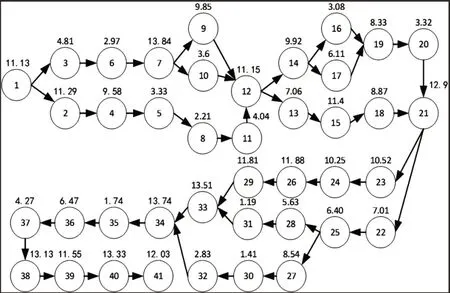
图4 作业优先顺序图Fig.4 Priority Sequence Diagram
3.3 基于启发式算法优化平衡方案
3.3.1 确定生产节拍
生产节拍(C)是指完成两个相同产品之间的间隔时间。也就是完成一个产品需要的平均时间。确定统一的生产节拍是实现均衡化生产的前提。节拍按照每天8h的有效工作时间计算,根据产品的订单量,Y1、Y2、Y3的平均日生产量分别为17、14、14辆。
混流装配装配线的节拍计算如式(2):

式中:C—混流装配线生产节拍;min;tx—生产期实际工作时间,min;Qi—生产期产品i的数量,辆;Ti—产品i的总作业时间,min。
确定混流装配线生产节拍后,需要对产线所需要的最小工位数进行求解,最小工位数(Hmin)是指装配线要在实际工作时间内完成计划产量所需要的最少工位数量。
混流装配线的最少工位数的计算如式(3):

根据式(3)计算出混流装配线的最少工位数,计算结果如下:

3.3.2 基于启发式算法进行优化
启发式算法优化混流装配线平衡一共需要4 个步骤,分别为:(1)确定生产节拍;(2)从第一个工位开始,对作业工序重新分配;(3)另重新分配的工位总时间等于或接近生产节拍;(4)计算得到的新的混流线的相关评价指标。根据以上步骤,玉米机混流装配线的平衡分析过程和优化结果,如表4、表5所示。
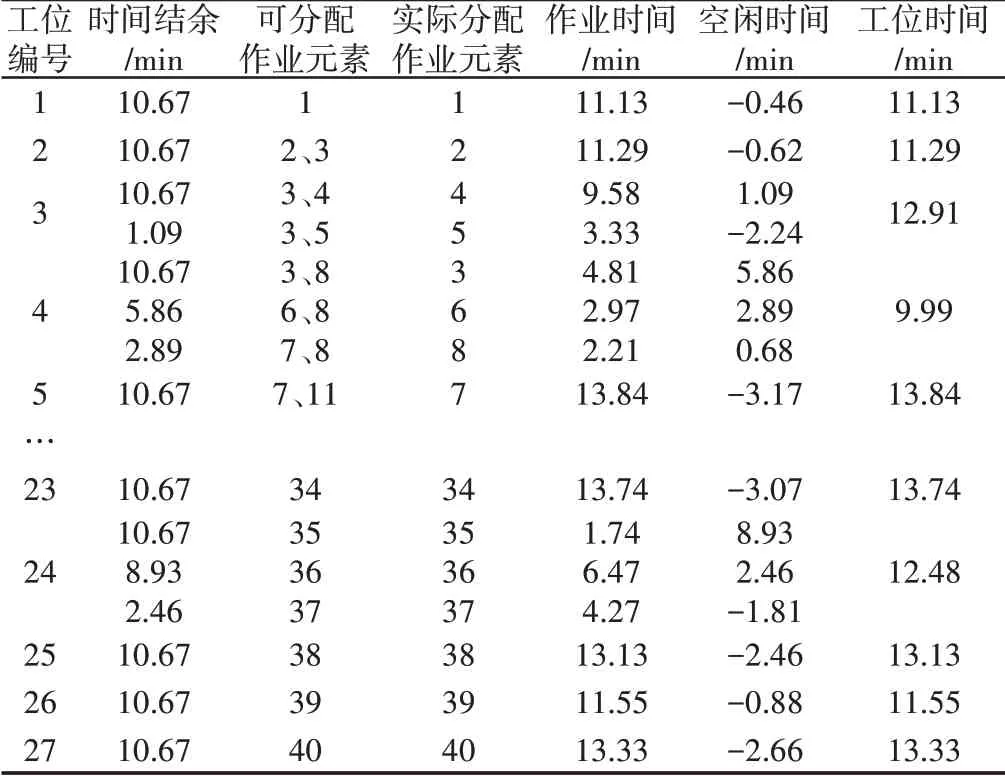
表4 玉米机混流装配线平衡分析过程Tab.4 Balance Analysis Process of Mixed-Model Assembly Line of Corn Harvester
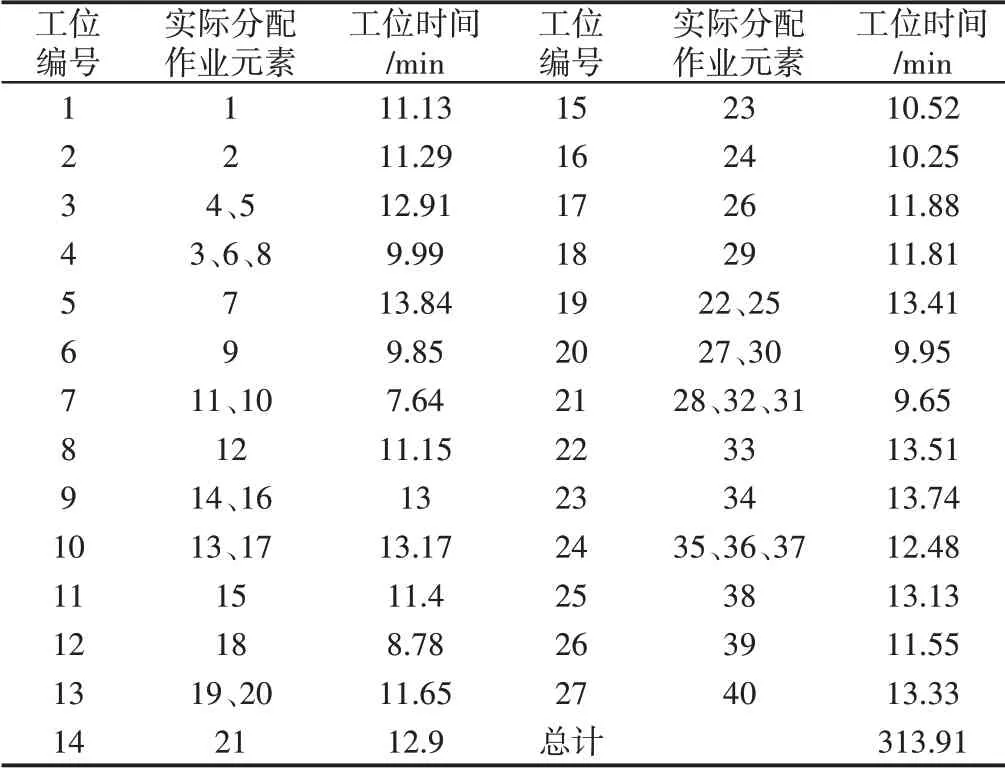
表5 玉米机混流装配线平衡结果表Tab.5 Balance Result of Mixed-Model Assembly Line of Corn Harvester
3.3.3计算混流装配线评价指标
混流装配线的平衡率计算如式(4):

式中:B—混流装配线的平衡率;
Tz—生产总计工位时间,min;
CTz—生产瓶颈工位时间,min;
H—生产工位总数量,个。
计算结果如下:
B=313.91/(13.84×27)×100%=84%
从计算结果可以得出:优化后玉米机混流装配线工位数为27时的总平衡率为84%。通过优化,Y1产品平衡率提高14.87%,Y2产品平衡率提高了22.7%,Y3产品平衡提高了17.96%。同时Y1装配线的瓶颈工时由原先的27.31min降低到13.84min,降低了13.47min;Y2装配线的瓶颈工时由原先的34.15min降低到13.84min,降低了20.31min;Y3装配线的瓶颈工时由原先的33.12min降低到13.84min,降低了19.28min;装配线整体的生产效率提高了一倍以上。
4 仿真验证
4.1 构建仿真模型
根据优化后的混流装配线,建立从产品开始生产到最后工位结束的完整装配过程的Flexsim动态仿真模型,仿真时间单位为min。建立仿真模型,需要4个步骤:(1)构建混流装配线设备布局,如图5所示。其中发生器表示物料仓库;处理器表示装配工位;吸收器表示成品库;(2)依据优化后每个工位装配时间等数据设置各工位装配时间参数;(3)确定加工周期,目前装配线作业时间为每周6天,每天有效作业时间480min,将仿真周期设定为一周,即2880min;(4)对模型进行代码编译,编译结束后重置运行模型。

图5 Flexsim仿真模型Fig.5 Flexsim Simulation Model
4.2 仿真结果分析
根据建立的仿真模型运行后可得到各工位负荷,如图6所示。
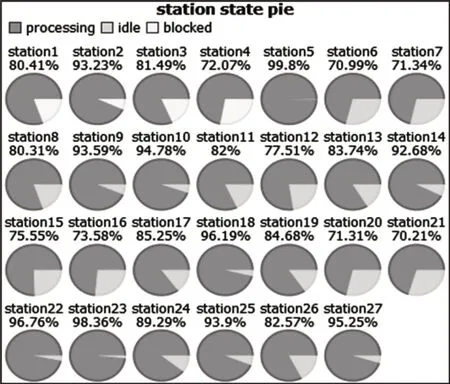
图6 各工位负荷图Fig.6 Load Diagram of Workstations
从图6中可以看出,通过优化,各工位负荷基本趋于平衡,各工位利用率均在70%以上,工位间等待现象和堵塞情况得到明显改善,整个生产系统畅通平衡,从而验证了优化方案的可行性。
5 结束语
这里针对某农机企业装配车间生产效率低下的问题,对三种具有混流装配特性的产品装配线进行了分析和优化,首先计算综合作业时间和绘制作业任务优先图,然后运用启发式算法对混流装配线进行了构建和优化,最后通过仿真验证了优化方案的可行性。
通过优化:
(1)提高了产线平衡率,优化后Y1产品平衡率提高14.87%,Y2产品平衡率提高了22.7%,Y3产品平衡提高了17.96%;
(2)直接节约了人工成本,该农机企业工人人均年收入为6万元/年,则Y1产品:节约人均人工成本=6×14.87%=0.89万元/年,Y2产品:节约人均人工成本=6×22.7%=1.36万元/年,Y3产品:节约人均人工成本=6×17.96%=1.08万元/年,由此可知,优化后直接节约人工成本3.33万元/年;
(3)优化后各工位负荷更均匀,提升了人员积极性,产线在制品堆积大大减少,减少了在制品库存。结果表明,运用启发式算法可有效解决农机企业混流装配线平衡问题,提高整体装配效率。

