基于分组蚁群算法的复杂零件视觉检测机器人路径规划*
□ 陈叶凯 □ 梁冬泰 □ 陈特欢 □ 彭文飞 □ 崔 杰
1.宁波大学 机械工程与力学学院 浙江宁波 315211 2.浙江华朔科技股份有限公司 浙江宁波 315000
1 研究背景
在现代化制造业中,复杂零件广泛用于自动化设备,结构特征复杂多样,在机器中价值高,品种多,并且要求在机器运行过程中稳定安全可靠。对于该类零件,须严格保证每个零件的质量,即须对每个零件的每个特征进行检测。
由于复杂零件特征多样且分布不均匀,使得检测任务繁重,仅依靠常规的人工检测,通常导致检测效率低下,同时由于零件种类繁多,使得检测过程复杂。设计一种机器人视觉检测系统,替代人工对零件特征进行检测,能够在很大程度上提升检测效率。
机器人视觉检测的关键点在于获得无碰撞最优路径,需要对机器人的检测路径进行规划。机器人路径规划过程主要包括检测目标建模、优化目标函数定义、目标点遍历寻优三个部分。
对检测目标在空间中的位姿进行建模,常用的建模方法有可视图法、拓扑网络法、栅格法等。其中,栅格法将检测目标分割成一系列的网格,根据网格内是否包含检测目标,对网格进行划分。张玮等[1]采用均匀栅格法进行二维平面建模,这种方法空间利用率低下,过多占用无障碍物空间,若将栅格划分过细,则会导致计算效率低下。优化目标函数在不同场景下有不同定义,王宇等[2]将总行程作为三维地形下的优化目标函数。机器人视觉检测路径不同于三维地形中的移动,需同时考虑位姿变换,总行程无法准确描述目标点之间的变化。
对目标点遍历寻优为典型的旅行商问题,解决算法主要有遗传算法、蚁群算法等[3-12]。蚁群算法广泛用于解决旅行商问题、避障、约束满足条件问题等。在求解旅行商问题时,随着目标点数量的增加,计算效率下降,为此,不少研究者对蚁群算法做出了改进。卜新苹等[7]采用非均匀栅格法对环境进行建模,用闵可夫斯基距离对障碍物进行边界拓展后,将移动物体视为质点,根据建模结果应用蚁群算法进行路径规划。使用非均匀栅格法对障碍物进行二维投影,忽略了障碍物的高度特征,难以适用于三维空间避障环境。Duan Haibin等[9]使用差分进化算法改进蚁群算法规划三维路径,将蚂蚁分成若干组,使用各组蚂蚁产生的信息素矩阵,对路径上信息素的更新策略进行改进,但是只对三维路径中的欧氏距离进行优化,优化过程中没有考虑物体姿态的变化。
在综合上述研究优缺点后,笔者提出一种基于分组蚁群算法的复杂零件视觉检测机器人路径规划算法。首先基于非均匀二叉树原理和检测目标的投影与高度特征,对机器人运动的三维空间进行建模。然后根据目标点位姿变换的特点,采用一种优化目标函数。最后基于分组蚁群算法求解图像采集的最优路径,根据手眼标定结果获得各采集点的机器人末端位姿,实现零件的图像采集。这一算法能够实现机器人在三维空间中位姿变换的路径规划,相比基本蚁群算法具有更高的计算效率,相比均匀栅格法具有更优的目标空间建模。基于分组蚁群算法的复杂零件视觉检测机器人路径规划流程如图1所示。

▲图1 复杂零件视觉检测机器人路径规划流程
2 目标空间建模
为避免机器人在遍历过程中与检测目标碰撞,对检测目标建模,在空间中描述检测目标。笔者基于二叉树分割六面体包络法对检测目标进行建模,具体思路为,将检测目标在高度、长度方向分解为多个实体,用多个六面体对各实体进行包络。
2.1 目标空间建立
目标空间A为目标在高度方向上的最小外接六面体。获得最小外接六面体的具体方法为,获得检测目标在高度方向上的投影,使用外接矩形包围投影,并通过不断变换外接矩形方向,共得到q个外接矩形。取最小的外接矩形作为目标空间底面,以此底面从目标高度最低点到最高点扫掠,得到六面体目标空间。
2.2 目标空间衡量
目标空间不应占用过多的机器人运动空间,以体积占比ρ来衡量所获目标空间的质量。
ρ=V1/V2
(1)
式中:V1为检测目标体积;V2为目标空间体积。
检测目标体积包括填补内部特征。
为得到满足体积占比要求的目标空间A,在高度和长度方向上用非均匀二叉树分割,不断对模型进行分割,计算分割后的体积占比,以体积占比作为分割结束指标。设置最大分割次数,直到体积占比满足要求或到达最大分割次数。
2.3 障碍物路径判断
目标空间为参数已知的六面体,定义障碍物路径为穿过目标一个或多个面的路径。
根据建模过程,所获六面体各面不一定与坐标系各面平行,存在角度δ旋转及Y轴方向yp偏置。在进行障碍物判断时,对平面及目标点同时旋转-δ。障碍物路径判断如图2所示。图2中,A1为某个面,A2为旋转-δ,并平移-yp后得到的平面,b1、b2为a1、a2跟随A1平面变换后的目标点,zmin、zmax分别为A1平面Z轴方向的最小值和最大值,xmin、xmax分别为A2平面X轴方向的最小值和最大值。

▲图2 障碍物路径判断
在旋转变换以后,只需根据简单的坐标关系,即可确定路径与目标空间平面的关系。
(1) 根据目标点b1、b2确定路径方程:
(x-x1)/U=(y-y1)/V=(z-z1)/W
(2)
式中:U、V、W依次为路径在X轴、Y轴、Z轴方向上的向量;(x,y,z)为路径上点b1和点b2之间点的坐标;(x1,y1,z1)为点b1的坐标。
(2) 令路径方程中y为0,求出路径与目标空间平面所在平面的交点坐标(x,y,z)。
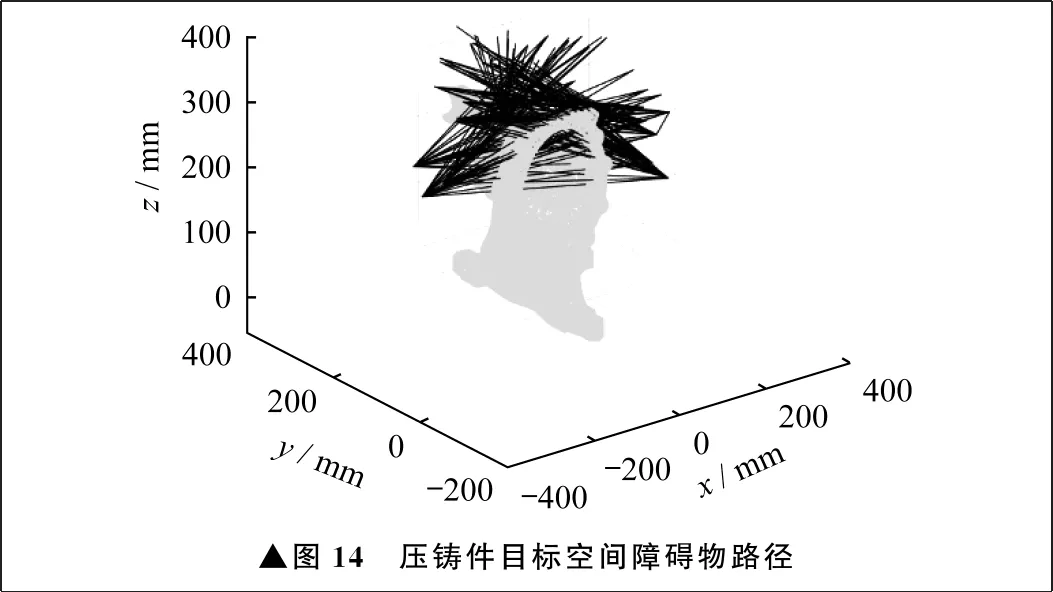
(3) 若xmin 利用路径与目标空间平面的关系,依次判断路径与目标空间六面的关系。路径与某个面相交,则判定当前路径为障碍物路径。路径与六个面都不相交,则判定为无障碍物路径。 机器人的遍历过程同时存在位置变换和姿态变换,并共同影响路径结果。笔者提出采用向量和优化目标函数来描述检测装置在机器人基坐标系下目标点之间的变换。 检测装置在两个目标点之间变换的直线欧氏距离d(ai,aj)为位置变换单目标函数,ai、aj为检测装置在目标点i处、j处的中心,向量pij为位置变换方向。 (3) pij=[xi-xjyi-yjzi-zj]T (4) 式中:(xi,yi,zi)、(xj,yj,zj)分别为ai和aj在机器人基坐标系下的坐标。 检测装置在每个目标点具有特定的姿态,为描述检测装置的姿态,检测装置在目标点i处的姿态向量λi定义为从检测目标上检测点中心αi指向检测装置中心ai方向上的单位向量。 λi=[xi-xαiyi-yαizi-zαi]T/ηi (5) (6) 式中:(xαi,yαi,zαi)为检测目标上检测点αi在机器人基坐标系下的坐标;ηi为姿态向量的模。 检测装置在目标点姿态相同的情况下,目标点i、j之间的欧氏距离即可表示优化目标。在综合考量位姿变换后,将各目标点在姿态向量方向偏移k个单位长度,得到新的目标点a′i,k为姿态变换相对程度。当检测装置在目标点i处、j处的姿态一致时,pij等于p′ij,相当于只进行位置变换。目标点间姿态相同时向量和如图3所示。 存在λi、λj与欧氏向量夹角同时为锐角的情况,此时满足锐角条件,对λi、λj同时取反向,以避免总优化 ▲图3 目标点间姿态相同时向量和 目标减小。λj为检测装置在目标点j处的姿态向量。满足锐角条件时向量和如图4所示。 ▲图4 满足锐角条件时向量和 (7) (8) p′ij=[xa′i-xa′jya′i-ya′jza′i-za′j]T (9) (10) 式中:(xa′i,ya′i,za′i)、(xa′j,ya′j,za′j)分别为新目标点a′i和a′j的坐标。 求ya′i、za′i、xa′j、ya′j、za′j与xa′i类似,当位置变换较大时,k取较小值,反之,k取较大值。在得到向量和后,使用目标向量和的模γij作为优化目标。 路径规划的核心在于获取最优的遍历路径。基于上述目标空间建模和优化目标函数,笔者提出一种分组蚁群算法来找寻最优路径。分组蚁群算法在相同的条件下,经验证具有更快的寻优速度。 蚁群算法中,蚂蚁在当前节点选择下一节点,依据路径上的信息素浓度和启发因子进行选择,在比较选择各未访问节点的概率γij后,采用轮盘赌选择下一访问节点。 (11) ξij=1/γij (12) 式中:τij为检测装置从目标点i到j路径上的信息素浓度;ξij为检测装置从目标点i到j路径上的启发因子;s、t分别为选择路径时信息素和启发因子的相对重要度;T为当前检测装置的目标点集合。 在蚁群算法中,蚂蚁在每次遍历过程中会在转移路径上留下信息素。蚂蚁在路径上留下的信息素浓度与路径长度成反比,每轮迭代完成后,信息素更新为上一轮信息素和本轮迭代蚁群留下的信息素的叠加。 (13) Δτh(i,j)=Q/Lh (14) 应用前述障碍物路径判断对路径分类后,设置障碍物路径上的启发因子为0,即蚂蚁在选择该路径时的概率为0,以避开对障碍物路径的访问。 在蚁群算法中,设置蚁群规模为m后,蚂蚁根据路径上的信息素和启发因子,各自完成对目标点的遍历。在此基础上,笔者提出分组蚁群算法,蚁群以分组的方式完成遍历。将蚂蚁分为g组,各组中各蚂蚁各自完成迭代,g组蚂蚁完成遍历表示一轮迭代完成。与基本蚁群算法相比,在消耗相同资源的情况下,分组蚁群算法具有更高的寻优效率。 各组蚁群完成寻优以后,根据路径长度对信息素矩阵进行排序,得到各组信息素矩阵τ1、τ2、...、τg,满足L1 τ=v1τ1+v2τ2+...+vgτg (15) v1+v2+...+vg=1 (16) v1>v2>...>vg>0 (17) 式中:τ为最终信息素矩阵;v1、v2、...、vg为各组信息素矩阵奖惩因子。 分组蚁群算法具体流程为:将蚂蚁分为g组后,各组独立进行目标点遍历;在各组完成一轮迭代后,进行信息素更新,并重新开始迭代,直到迭代次数达到最大迭代次数I。 适度函数用于评价算法对于应用场景的适用性。针对多样性复杂零件检测过程,评价指标主要为遍历路径长度和算法运算效率。遍历路径长度决定单次遍历的时间,算法运算效率决定对单个检测进行路径规划的时间。在综合考虑上述因素以后,将适度函数S定义为: (18) w1+w2=1 (19) 式中:w1、w2分别为路径长度权重和寻优时间权重,L、T分别为得到的路径长度和寻优时间,转换至相同数量级;C1、C2分别为路径长度适度常数和运算时间适度常数。 ▲图5 手眼标定 笔者选用发动机缸体作为算例检测目标,硬件平台为戴尔台式机,内存为8 GiByte。对发动机缸体表面特征进行分析以后,采用所提出的检测目标空间进行建模,应用目标函数、分组蚁群算法对发动机缸体表面的122个检测点进行路径规划。发动机缸体如图6所示。 ▲图6 发动机缸体 发动机缸体表面检测目标空间建模通过非均匀二叉树分割得到。为验证方法的可行性,与均匀栅格法进行对比。为准确且高效地计算障碍物路径,设置体积占比为0.6,最大分割次数为5,旋转步长为1°。非均匀二叉树分割的结果为,在长度方向上非均匀分割六份,在高度方向上均匀分割四份。均匀栅格法分割结果为,在长度方向上均匀分割五份,在高度方向上均匀分割四份。发动机缸体非均匀二叉树分割法建模如图7所示,发动机缸体均匀栅格法建模如图8所示,发动机缸体不同建模方法结果对比见表1。 ▲图7 发动机缸体非均匀二叉树分割法建模▲图8 发动机缸体均匀栅格法建模 在完成检测目标空间建模后,对检测目标点之间的7 381条路径按障碍物进行分类。笔者采用非接触式检测,不需要考虑检测装置存在一定体积与检测目标发生碰撞的情况,直接将检测装置作为质点。在当前目标空间中,障碍物路径数量为4 752条,无障碍物路径数量为2 659条。无障碍物路径如图9所示。 表1 发动机缸体不同方法建模结果对比 ▲图9 无障碍物路径 设置算法参数,蚁群规模m为20,信息素重要度s为5,启发因子重要度t为5,分组数量g为5,信息素蒸发率σ为0.1,信息素增强因子Q为11,最大迭代次数I为200,路径长度权重w1为0.4,计算时间权重w2为0.6,路径长度适度常数C1为105,计算时间适度常数C2为102,奖惩因子v1为0.5,v2为0.2,v3为0.2,v4为0.1,v5为0,姿态变换相对程度k为10。 发动机缸体表面检测路径规划分组蚁群算法与基本蚁群算法对比见表2。由表2数据可知,分组蚁群算法在计算时间上缩短了19.5%,且获得的路径相对于基本蚁群算法在长度上更优。同时,分组蚁群算法的适度比基本蚁群算法高21.6%,即相对于基本蚁群算法,分组蚁群算法更适合用于多品种零件检测的路径规划。基本蚁群算法和分组蚁群算法路径规划结果分别如图10、图11所示。 ▲图10 基本蚁群算法路径规划结果 ▲图11 分组蚁群算法路径规划结果 表2 发动机缸体表面检测路径规划算法对比 为验证分组蚁群算法的实际使用效果和针对不同零件的通用性,另外选取某压铸件为检测目标进行实例验证。使用UR5机器人,检测装置由工业相机和四个条形光源组成,条形光源从四个方向给予照明,工业相机的镜头为55 mm焦距远心镜头,试验平台如图12所示。在完成相机和UR5机器人手眼标定后,通过分组蚁群算法运算得到路径,在示教器上编程完成路径遍历,同时完成检测目标点的图像获取。 ▲图12 试验平台 压铸件的目标空间建模参数与发动机缸体相同,压铸件目标空间建模结果如图13所示,数据见表3。 ▲图13 压铸件目标空间建模结果 表3 压铸件建模数据 在完成检测目标空间建模后,对检测目标点之间的1 225条路径按是否有障碍物进行分类。在当前目标空间中,障碍物路径的数量为189条,无障碍物路径的数量为1 036条,障碍物路径如图14所示。 ▲图14 压铸件目标空间障碍物路径 在对压铸件上的目标检测点进行路径规划时,设置信息素增强因子C为1,其余参数与发动机缸体相同。在运算得到路径点的运动顺序后,在UR5机器人上编程,完成目标点的遍历试验。分组蚁群算法寻优结果为,最优路径长度为17 515 mm。压铸件目标点路径规划结果如图15所示。 ▲图15 压铸件目标点路径规划结果 机器人遍历过程未与压铸件发生碰撞,即分组蚁群算法能够在实际使用中高效地计算出最优路径,并且能够保证路径无碰撞,同时在各个位置获得的图像清晰,手眼标定结果准确。 在完成手眼标定后,逐一计算在各目标点上机器人的末端位姿,并在UR5机器人示教器上编程控制机器人运动。UR5机器人遍历过程及图像获取结果如图16所示。由图16可以看出,在目标点获得的图片较清晰,标定结果准确。 ▲图16 UR5机器人运动过程和图像获取结果 笔者研究了复杂零件视觉检测机器人路径规划问题,主要包括检测目标空间建模、优化目标函数定义、路径规划三部分。在检测目标建模阶段,采用非均匀二叉树分割检测目标,将检测目标转换为六面体,描述检测空间中的障碍物区域,增加机器人可运动的范围。 笔者提出应用向量和优化目标函数,同时考虑位置变换和姿态变换在不同度量下对路径的影响。在路径规划中,通过分组蚁群算法规划检测路径,在综合考量路径结果和计算效率的前提下,有效找到机器人无碰撞检测的最优路径。算例和实例结果表明,分组蚁群算法在计算效率上明显优于基本蚁群算法,在规划最短路径的长度上也优于基本蚁群算法,并且不易陷入局部最优。3 优化目标函数
3.1 位置变换单目标函数
3.2 姿态向量
3.3 向量和目标函数


4 路径规划
4.1 路径点选择策略
4.2 信息素更新策略

4.3 避障
4.4 分组寻优
4.5 分组信息素更新策略
4.6 适度函数
5 手眼标定

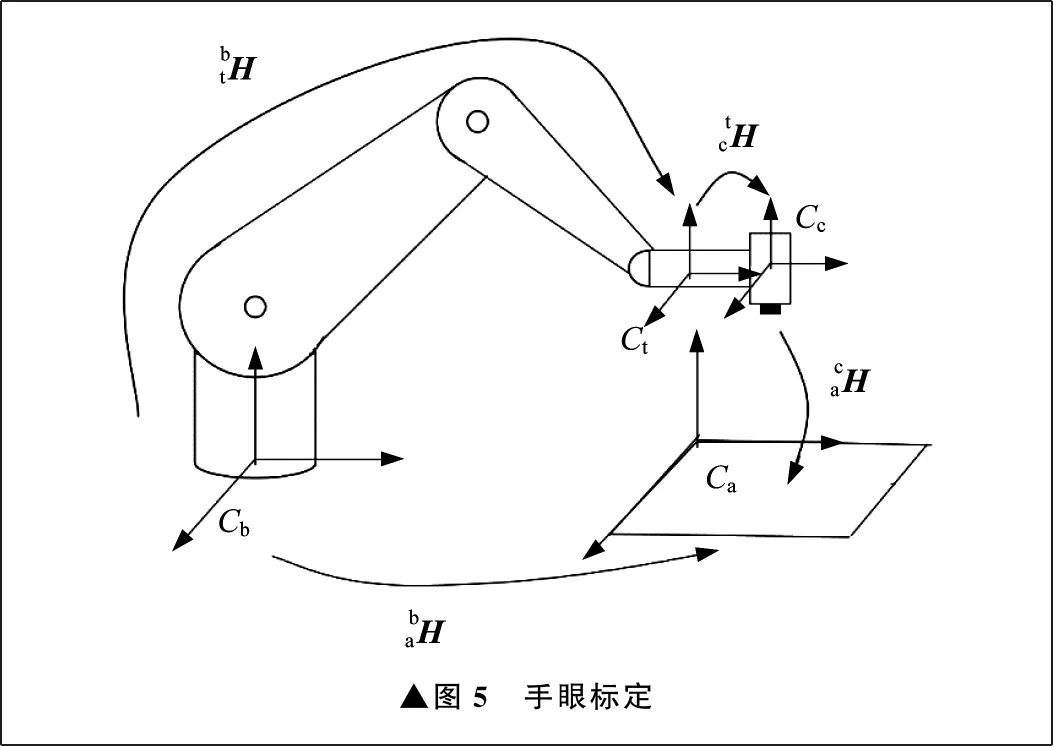
6 试验分析
6.1 路径规划算例检验

6.2 检测目标空间建模与障碍物判断



6.3 蚁群寻优



6.4 实例验证





7 结束语

