正交胶合木墙体-楼板角撑连接节点受火后受剪承载力计算方法

张 晋 姜 坤 陆 川

(1东南大学混凝土及预应力混凝土结构教育部重点实验室， 南京211189)(2华润置地有限公司， 南昌330000)

正交胶合木(CLT)可用于建筑的墙体、楼面板与屋面板结构，适用于建造高层木结构建筑[1].长久以来，木结构建筑的发展一直被木材的抗火性能所限制，因此，研究CLT的抗火性能对多高层木结构的推广及应用具有重要意义.CLT节点是CLT结构中受力的关键部位，也是设计中最复杂的部分.CLT节点的抗火性能关系到火灾下及火灾后结构的安全性，需要对其开展深入研究.

目前，国内外关于CLT节点抗火性能方面的研究文献较少.Dagenais[2]对4种不同形式的CLT板-板直线式节点进行了耐火试验研究，发现板-板直线式节点在火灾下均由于失去防火完整性而达到耐火极限，采用单侧或双侧盖板节点的楼板的耐火性能优于半层搭接节点连接的楼板，企口连接节点的楼板耐火性能最差；根据试验数据，验证其建立的有限元传热模型、热-力耦合模型和简化设计模型，并给出了4种不同形式的CLT板-板节点的完整性系数，用于简化设计方法，评估节点接缝的防火完整性.Mahr等[3]为了表征CLT节点的热降解效能，将CLT墙体-楼板角撑连接节点暴露于28种不同时间-温度组合的试验条件下，对节点进行循环剪切试验，进而提出骨架曲线模型，并发现随着温度的升高，节点的承载能力、弹性刚度、延性及耗能能力逐渐下降.

国内外目前尚未有公开文献介绍关于CLT墙体-楼板角撑连接节点受火后受剪承载力的计算方法；但是常温下CLT墙体-楼板角撑连接节点的受剪承载力计算方法已有一些基础性的研究，主要包括适用于CLT层板的销轴类紧固件受剪承载力以及轴向承载力的计算方法.欧洲规范EN 1995-1-1[4]中提供了常温下木-金属连接件的受剪承载力计算公式，但并不适用于CLT. Uibel等[5]进行了大量自攻螺钉在CLT上的受剪承载力试验研究，通过试验结果修正了欧洲规范EN 1995-1-1计算方法中的部分公式，使之能够适用于CLT，其修正内容包括：①对层板厚度小于等于9 mm的CLT板，拟合出销槽承压强度计算公式，并建议对层板厚度大于9 mm的CLT板，仍采用欧洲规范EN 1995-1-1中的推荐公式计算销槽承压强度；②给出了钉入CLT中自攻螺钉的轴向抗拔承载力计算公式；③对于垂直钉入CLT平面内的多个自攻螺钉，认为其有效个数与实际个数相同，即总受剪承载力等于各个紧固件受剪承载力之和.

基于贾苑等[6]对常温下CLT节点受剪性能的试验研究，本文对较为常用的CLT平台式墙体-楼板角撑连接节点开展常温及受火后受剪试验.根据常温下CLT节点受剪承载力计算方法，考虑节点受火后钢销轴强度折减及CLT层板有效持力截面的减少，提出了CLT墙体-楼板角撑连接节点受火后受剪承载力的计算方法，并通过试验结果验证其正确性与适用性.

1 试验

1.1 试验设计

设计了4组共计10个CLT墙体-楼板角撑连接节点试件，试件参数见表1.

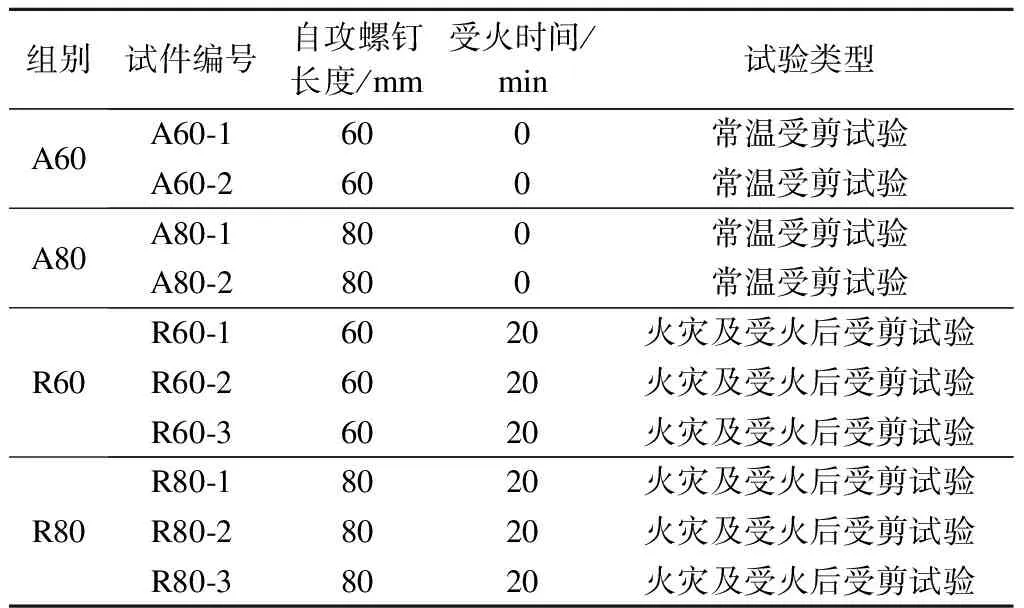
表1 试件设计参数

如图1所示，CLT墙体及楼板通过8根自攻螺钉与角钢连接件组成一个墙体-楼板角撑连接节点.CLT墙体、楼板的尺寸均为300 mm×300 mm×125 mm[6]，层数均为5层,每层厚25 mm.

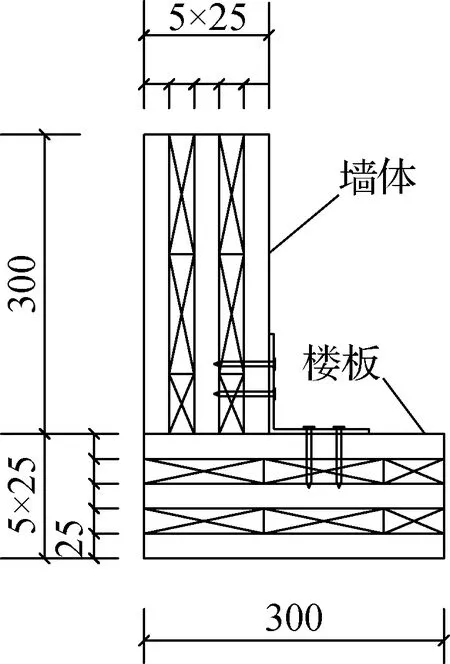
(a) 左视图

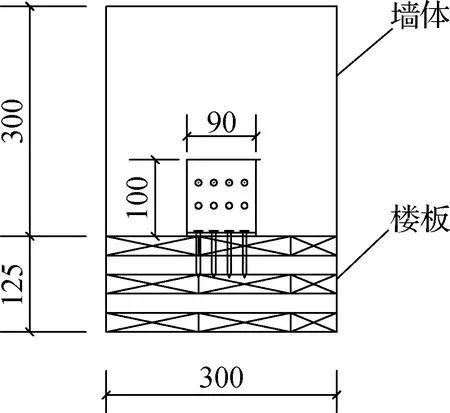
(b) 正视图

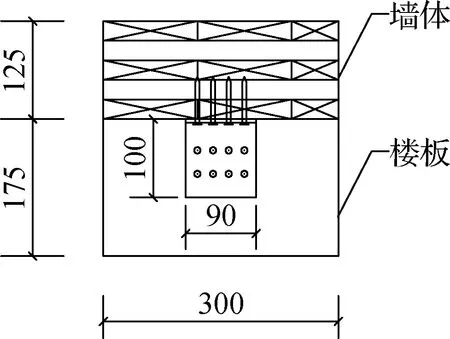
(c) 俯视图

1.2 材料性能

本试验所用的木材为北美加拿大进口的云杉-松木-冷杉(SPF)，由CANFOR公司生产，材质等级为2级.SPF板材经干燥处理后运至浙江宁波中加低碳有限公司加工成CLT幅面板.为了确定5层CLT板的力学性能，按照文献[7-10]进行材性试验，获得常温下各材性参数均值如下：板材密度为436.1 kg/m3，含水率为13.4%，滚动剪切强度为1.15 MPa，滚动剪切模量为23.31 MPa，5层顺纹层层板抗压强度为33.38 MPa，5层顺纹层层板抗压弹性模量为6.33 GPa.

节点的紧固件采用上海美固澄梵紧固件有限公司的DKM型自攻螺钉，材质为304不锈钢，选用60、80 mm两种长度规格，其他参数见表2.

表2 自攻螺钉几何参数 mm

依据文献[11-12]，对自攻螺钉开展抗弯试验和抗拔试验，测得的各力学性能参数均值如下：自攻螺钉STS-60的屈服弯矩为4 851 N·mm，抗拔强度为15.64 MPa；自攻螺钉STS-80的屈服弯矩为4 212 N·mm，抗拔强度为16.11 MPa.自攻螺钉STS-60的屈服弯矩大于自攻螺钉STS-80，这是由于前者受自身长度限制，加载点位于螺纹杆内，与规范要求的做法存在一定的出入.故偏于保守考虑，在下文计算中将2种自攻螺钉的屈服弯矩皆取为4 212 N·mm.

角钢连接件采用意大利Rothoblaas公司的标准产品HT100，具体尺寸为90 mm×100 mm×100 mm，厚度为3 mm.材质为镀锌高强结构钢(S250GDZ275)，由厂家提供的抗拉屈服强度平均值为250 MPa，极限抗拉强度平均值为330 MPa.

1.3 火灾试验

火灾试验在大型水平火灾试验炉中进行，采用ISO834标准火灾升温曲线.

如图2(a)所示，隔火区域采用20 mm厚耐火棉(苏州伊索来特耐火纤维有限公司产品，型号为ISOWOOL1260)进行包裹，并在耐火棉外侧再覆盖1层9 mm厚的普通石膏板(北新集团建材股份有限公司龙牌耐火纸面石膏板).试件在水平火灾试验炉中倒挂放置(见图2(b))，墙体的受火面为侧火面，楼板的受火面为迎火面.

试验中采用K型热电偶测量炉温和CLT节点内部温度.

待受剪试验结束后，取图3中的截面A-A′和B-B′作为测量面.将测量面切开，沿截面宽度方向每隔4 mm依次测量剩余截面厚度，再由试件原截面厚度减去剩余截面厚度，即可得到炭化深度.

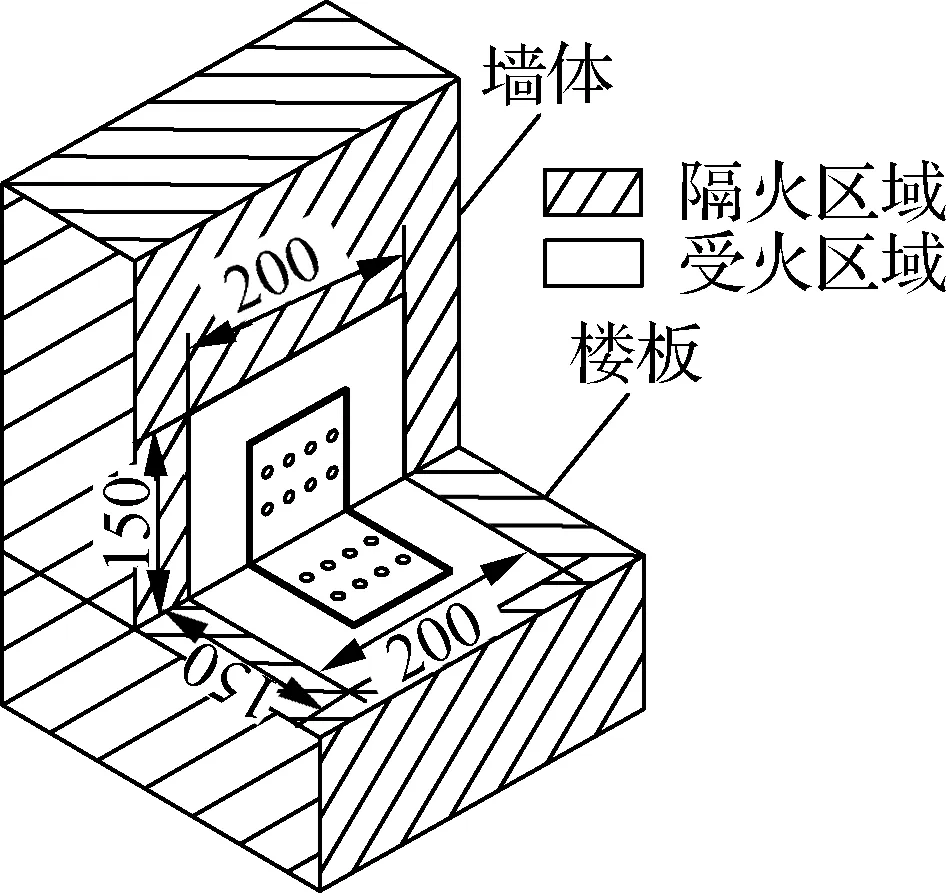
(a) 试件受火、隔火区域

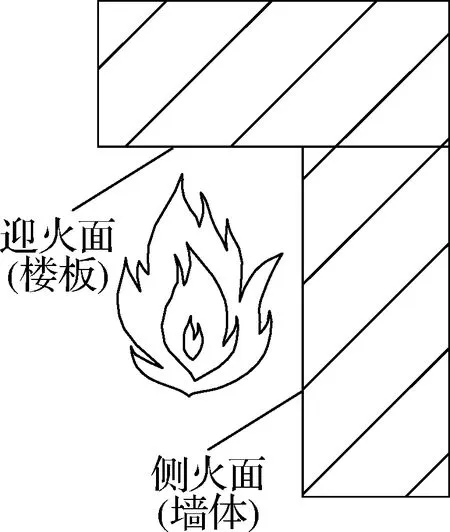
(b) 试件受火方位

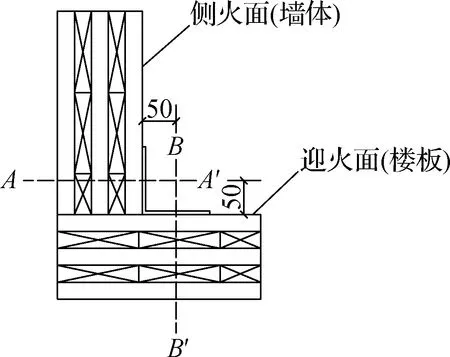
图3 炭化深度测量截面(单位：mm)

最终测得的各组试件炭化深度平均值如下：R60组试件迎火面炭化深度为15.48 mm，侧火面炭化深度为13.88 mm；R80组试件迎火面炭化深度为15.47 mm，侧火面炭化深度为14.20 mm.由于迎火面炭化深度大于侧火面炭化深度，故为了保守考虑，取迎火面炭化深度来验证炭化深度计算方法的适用性.

1.4 受剪试验

常温及受火后受剪试验采用同样的加载方式及测量方案.

为保证试件在加载过程中，墙体与楼板只存在一个方向的相对平动，设计如图4(a)所示的加载装置.墙体在对穿丝杆作用下被固定于钢板底座与反力梁之间，墙体的面外转动主要靠厚钢板约束；楼板Z向加载依靠千斤顶实现.单调加载静力试验参照文献[13]中的加载方式，配合使用机械千斤顶与位移计实现单调位移加载，加载速率取为5 mm/min[14].

图4(a)中，位移计1用于记录楼板沿加载方向(Z向)的位移；位移计2、3用于观测楼板加载过程中面外的转动，即记录X向和Y向的位移.试件沿加载方向的荷载-位移曲线见图5.

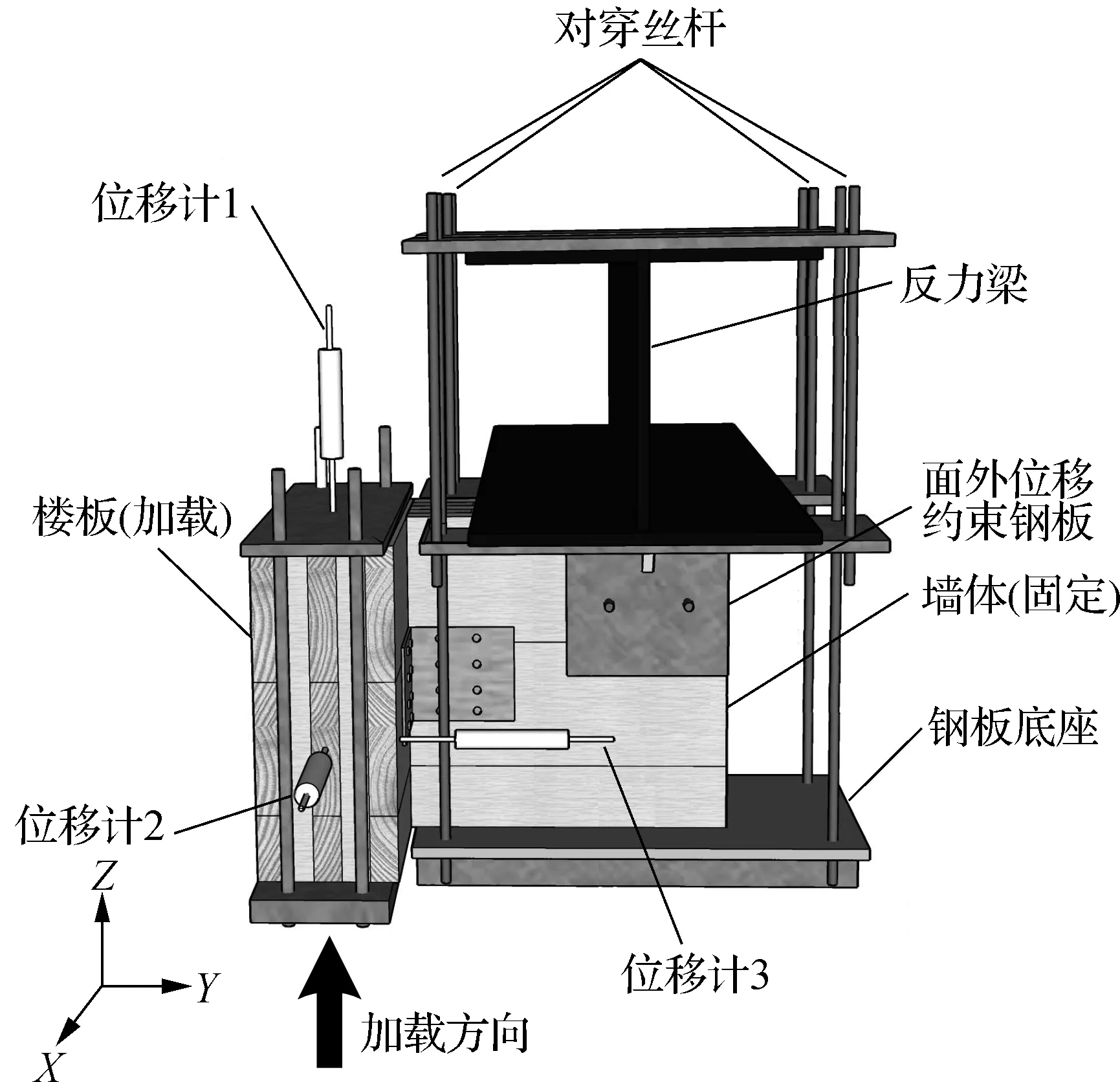
(a) 试验加载装置

(b) 试验现场

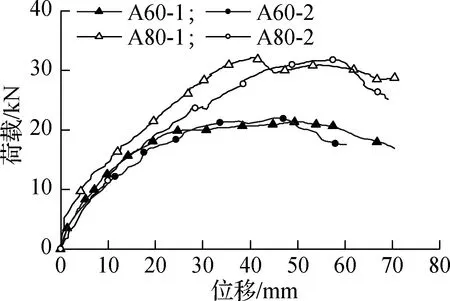
(a) 常温试件

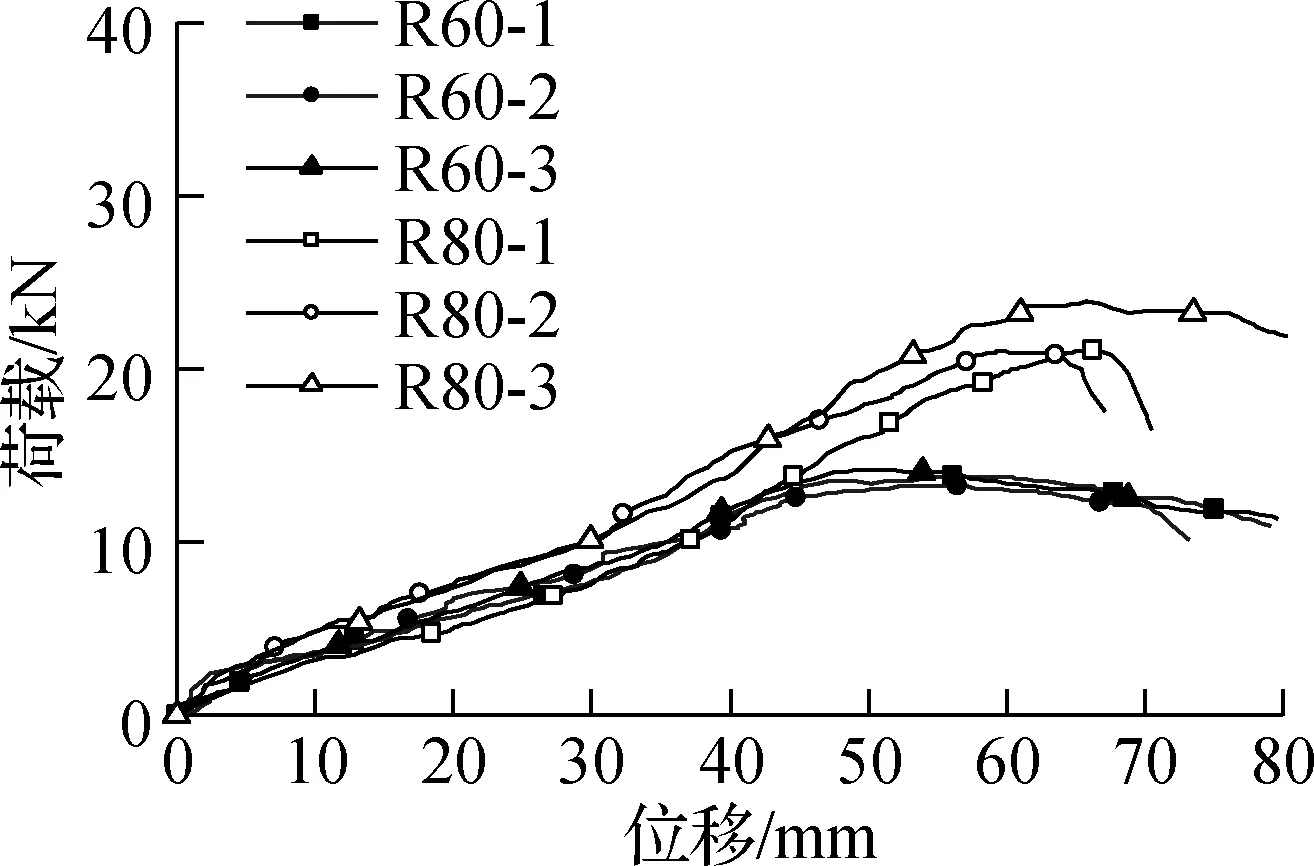
(b) 受火后试件

采用欧洲标准EN 12512—2001[14]中的力学特征值分析方法，对图5中的荷载-位移变化曲线进行计算，得到各组试件的平均初始刚度K、平均屈服荷载Fy、平均屈服位移Vy、平均极限位移Vu和平均延性系数d，结果列于表3.

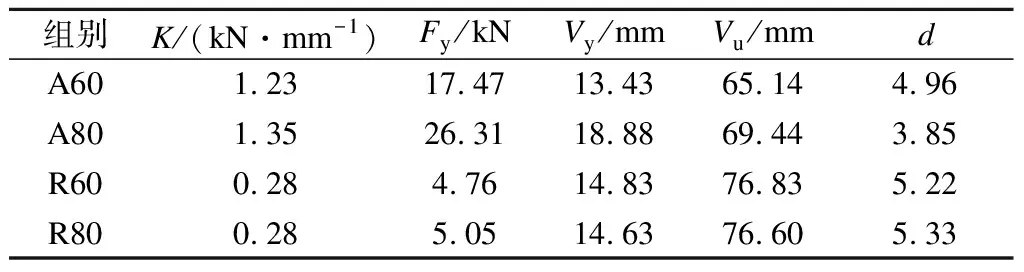
表3 试件力学性能参数

由表3可知，对于常温试件，A80组试件的平均初始刚度为1.35 kN/mm，为A60组试件的1.10倍；A80组试件的平均屈服荷载为26.31 kN，为A60组试件的1.51倍；A80组试件的平均延性系数为3.85，为A60组试件的0.77倍.由此可知，将60 mm长的自攻螺钉增加至80 mm，能有效提高试件的初始刚度和受剪承载力，但会降低延性.

对于受火后试件，R60组与R80组试件的平均初始刚度均为0.28 kN/mm；R80组试件的平均屈服荷载为5.05 kN，为R60组试件的1.06倍；R80组试件的平均延性系数为5.33，为R60组试件的1.02倍，两者相差不明显.因此，将自攻螺钉的长度由60 mm增至80 mm，对受火后试件的初始刚度、屈服荷载以及延性的提高基本无影响.

对比试件受火前后的力学性能可知，R60组试件与A60组试件相比，初始刚度降低了77%，屈服荷载降低了73%，延性系数提高了5%；R80组试件与A80组试件相比，初始刚度降低了79%，屈服荷载降低了81%，延性系数提高了38%.故试件受火后，初始刚度和屈服荷载会大幅降低，但延性会有所提高.

2 CLT墙体-楼板节点受火后受剪承载力计算方法

基于CLT层板销轴类紧固件常温受剪承载力计算方法，本文提出了一种用于计算CLT墙体-楼板角撑连接节点受火后受剪承载力的计算方法，其计算步骤如下：

①对钢材受火后力学性能进行定量折减；

②求解CLT层板受火后的非持力层厚度；

③确定销轴类紧固件受剪承载力计算公式中的等效销槽承压长度和轴向承载力计算公式中的有效钉入长度；

④采用考虑附加弯矩影响的受剪承载力计算公式来计算节点受火后的受剪承载力.

2.1 钢材受火后力学性能折减

为了简化处理，本文认为受火时自攻螺钉所经历的最高温度与受火时的环境温度相同，且自攻螺钉温度沿钉轴分布均匀.根据受火时间及ISO834标准火灾升温曲线，可以确定受火时钢材所经历的最高温度，进而确定钢材屈服强度的折减系数.一般钢材高温后的屈服强度折减系数可以参考文献[15]取值；不锈钢高温后的屈服强度折减系数可依据文献[16]确定.

2.2 CLT层板非持力层

木材受火时的截面区域通常分为常温层(20 ℃)、过渡层(20～300 ℃)及炭化层(>300 ℃).本文对这3个区域提出了如下假设：①常温层为有效截面区域.②炭化层完全无法承载，为非持力层.③100～300 ℃的过渡层区域在恢复至常温后，材性会发生一定的劣化；20～100 ℃的过渡层区域在恢复至常温后，材性能完全恢复[4].故本文认为20～100 ℃的过渡层区域为有效截面区域，即不折减区；100～300 ℃的过渡层区域为折减区.将折减区的材性折减转化为厚度折减，将折减区等效为零强度层与全强度层，其中零强度层为非持力层，全强度层为有效截面区域.④非持力层包含炭化层和折减区零强度层.

2.2.1 炭化层厚度

基于美国木结构设计规范[17]采用的木材平均炭化速率公式，提出炭化层厚度的计算公式为

dchar=βtt=2.15βnt-0.187t=2.15βnt0.813

(1)

式中，βt为木材的平均炭化速率；βn为木材1 h的名义线性炭化速率，此处取为0.635 mm/min；t为受火时间.

根据式(1)求得试件角钢连接区域下CLT的炭化深度，并与实测值进行比较，结果见表4.由表可知，炭化深度计算值与实测值吻合良好，且偏于保守.

表4 炭化层厚度实测平均值与计算值对比

2.2.2 折减区厚度

将木材简化考虑为半无限体，则受火后过渡层内木材温度T的分布规律可表示为[18]

(2)

式中，Ti为环境温度；Tp为木材开始炭化的温度；x为过渡层内离炭化层边缘的距离；a为过渡层厚度，此处取为35 mm.

为确定过渡层中折减区的厚度，将Ti=20 ℃，Tp=300 ℃，T=100 ℃代入式(2)中，计算得到x=16.3 mm.如图6所示，过渡层内靠近炭化层的 16.3 mm厚的部分为折减区，其余部分为有效截面区.

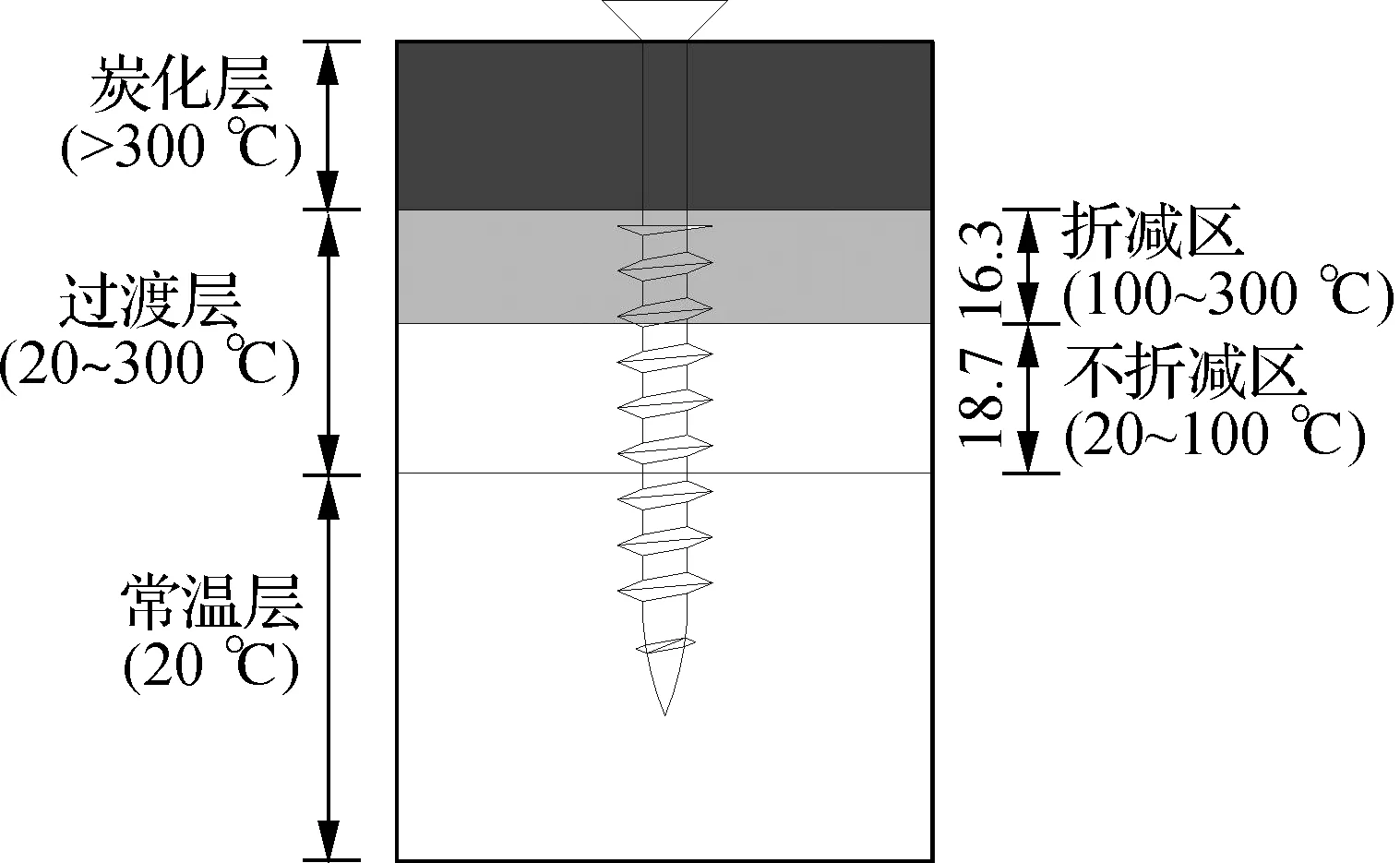
图6 折减区与不折减区示意图(单位：mm)

2.2.3 全强度层等效厚度

按自攻螺钉作用方向，折减区可分为顺纹受力层与横纹受力层.令Th为木材所经历的最高温度，在100～250 ℃之间取值；th为木材在最高温度下所经历的时间，在15～45 min之间取值.文献[19]给出了不同Th与th组合下的木材顺纹层与横纹层的抗压强度计算式.本文补充了如下假定：①300 ℃时木材的强度折减系数为0；②250～300 ℃区间内木材高温后的强度折减系数呈线性变化.则高温后木材顺纹受力层和横纹受力层的抗压强度折减系数分别为

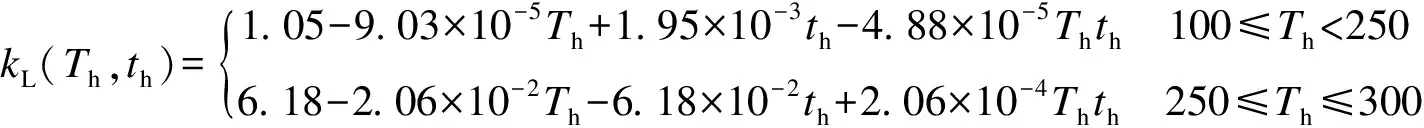
(3)

(4)

令Th=T，将式(2)分别代入式(3)和(4)中，并取th=20 min，Ti=20 ℃，Tp=300 ℃，a=35 mm，则顺纹受力层抗压强度折减系数kL(x)和横纹受力层抗压强度折减系数kR(x)分别为

(5)

(6)

参考美国木结构设计规范[17]中将顺纹、横纹销槽承压强度修正转换为销槽承压长度修正的处理方法，将受火后折减区的材性折减近似转换为厚度折减，将折减区等效为零强度层与全强度层.其中，全强度层厚度包括顺纹受力层等效厚度hL,e与横纹受力层等效厚度hR,e，其计算公式分别为

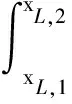
(7)

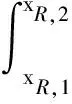
(8)

式中，xL,1、xL,2分别为炭化层与顺纹受力层的最近距离和最远距离；xR,1、xR,2分别为炭化层与横纹受力层的最近距离和最远距离.

则全强度层等效厚度he为

he=hL,e+hR,e

(9)

2.2.4 非持力层厚度

非持力厚度hinv的计算公式为

hinv=dchar+(16.3-he)

(10)

式中，16.3-he的几何含义为零强度层厚度.

2.3 等效销槽承压长度及有效钉入长度

受火后自攻螺钉在CLT中的等效销槽承压长度hc的计算公式为

hc=hini-hinv

(11)

式中，hini为受火前销槽承压长度，取受火前CLT厚度和紧固件穿入深度中的较小值.

有效钉入长度lef取自攻螺钉螺纹长度和等效销槽承压长度与钉尖长度差值中的较小值.

2.4 考虑附加弯矩的受剪承载力计算式改进

欧洲规范EN 1995-1-1中常温下木-金属连接件的受剪承载力计算公式包含Johansen屈服理论承载力项[20]以及绳索效应承载力提高项.

CLT墙体-楼板角撑连接节点受火后会在角钢连接件与层板之间产生非持力层，导致在自攻螺钉上产生一个附加弯矩.考虑受附加弯矩影响，应对常温下木-金属连接件的受剪承载力计算式中的Johansen屈服理论承载力项进行修正.该非持力层的存在也会导致自攻螺钉有效钉入长度的减少，因此由绳索效应提高的承载力也应予以修正.

2.4.1Johansen屈服理论承载力项修正

基于Johansen屈服理论承载力计算方法，给出以下假设[4]：①销槽承压和销承弯的应力-应变关系为理想刚塑性本构模型.②不考虑构件在剪切面之间的摩擦.③钢板不会发生销槽承压屈服，钢板对销的剪力作用在剪切面上，且以钢板厚度与销直径的相对关系区分薄厚钢板.④为薄钢板时，钢板对销转动无约束能力，钢板边缘只可能发生销刚体转动屈服以及侧构件单个塑性铰屈服；为厚钢板时，钢板对销的转动存在足够的钳制作用，销的塑性铰只会发生在钢板边缘，即剪切面上只可能发生主构件销槽承压屈服、主构件单个塑性铰屈服以及双塑性铰屈服.

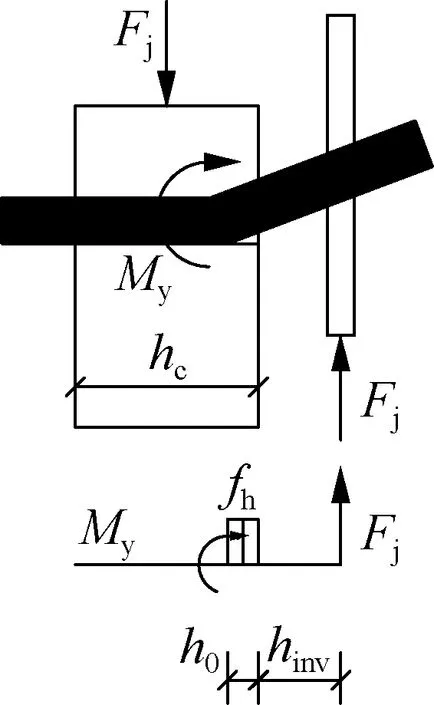
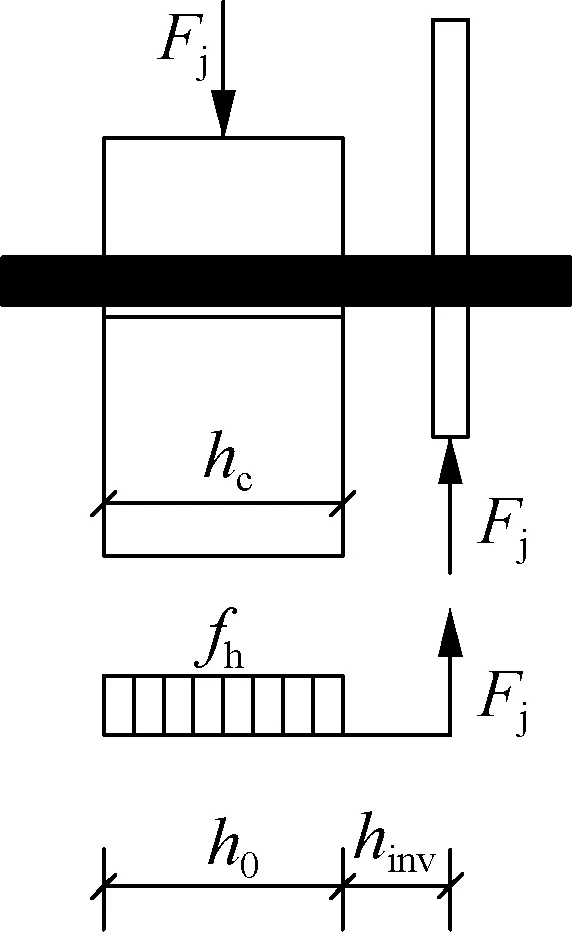
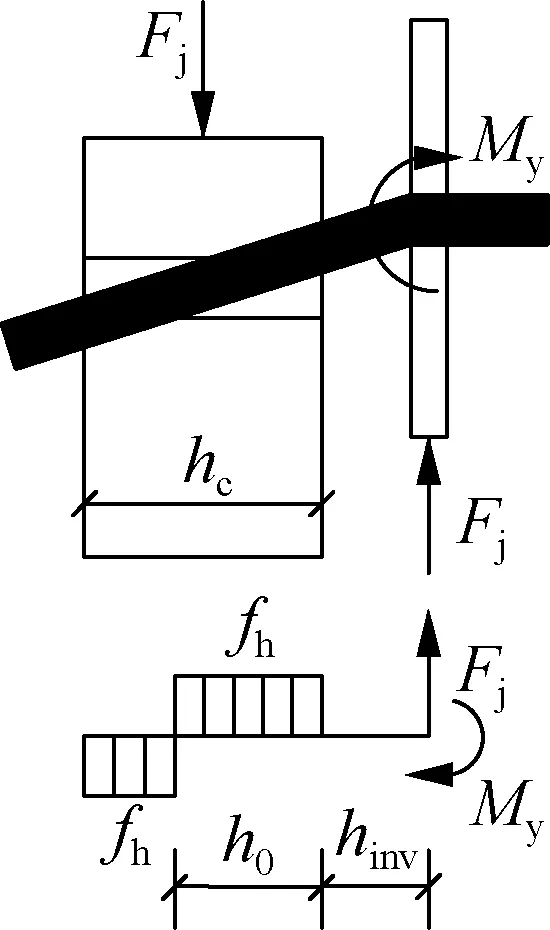
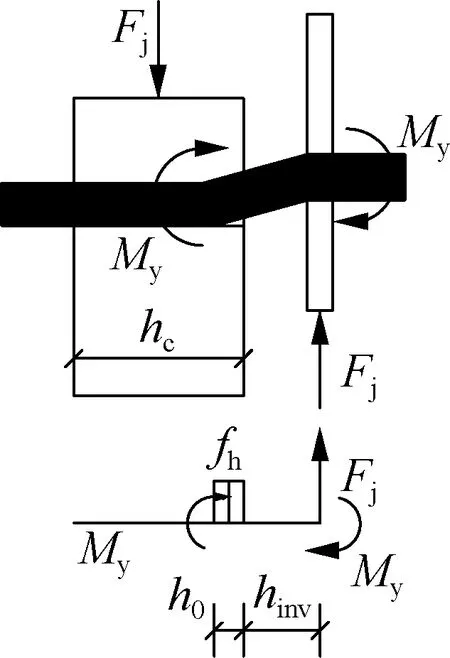
图7为考虑附加弯矩作用时各屈服模式下木-金属连接件的应力分布图.图中，Fj为Johansen屈服理论承载力；My为钢销轴的屈服弯矩；fh为木材销槽承压强度；h0为木材中靠近剪切面的应力分布长度；def为钢销轴的有效直径，对于螺钉应考虑螺纹部分的效应，取值为螺纹内径的1.1倍.

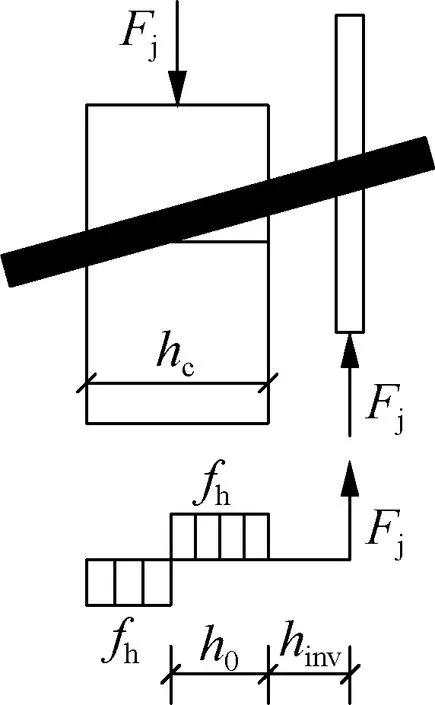
(a) 销刚体转动屈服

(b) 侧构件单个塑性铰屈服

(c) 主构件销槽承压屈服

(d) 主构件单个塑性铰屈服

(e) 双塑性铰屈服

销刚体转动屈服时(见图7(a))，薄钢板无法约束销转动，钢板边缘不存在弯矩，由钢板边缘力矩平衡可得

(12)

计算可得

(13)

由剪力平衡可得

Fj=[h0-(hc-h0)]fhdef=

(14)

侧构件单个塑性铰屈服时(见图7(b))，薄钢板无法约束销转动，钢板边缘不存在弯矩，由钢板边缘力矩平衡可得

(15)

计算可得

(16)

由剪力平衡可得

(17)

主构件销槽承压屈服时(见图7(c)),由剪力平衡可得

Fj=fhdefh0=fhdefhc

(18)

主构件单个塑性铰屈服时(见图7(d)),厚钢板对销存在足够的钳制作用，塑性铰出现在钢板边缘，由钢板边缘力矩平衡可得

(19)

计算可得

(20)

由剪力平衡可得

Fj=[h0-(hc-h0)]fhdef=

(21)

双塑性铰屈服时(见图7(e)),厚钢板对销存在足够的钳制作用，塑性铰出现在钢板边缘，另一塑性铰出现在木材内，由钢板边缘的力矩平衡可得

(22)

计算可得

(23)

由剪力平衡可得

(24)

2.4.2 绳索效应承载力提高项修正

欧洲规范EN 1995-1-1认为，在侧构件单个塑性铰屈服、主构件单个塑性铰及双塑性铰屈服的破坏模式下，需要考虑绳索效应所提供的承载力，其大小为紧固件抗拔承载力的1/4，且不大于Johansen屈服理论承载力.

紧固件采用自攻螺钉且钉于CLT中，其抗拔承载力Fax的计算公式为[5]

(25)

式中，d为自攻螺钉外径;ε为自攻螺钉轴线与木纹的夹角，垂直钉入时取ε=90°;ρk为CLT密度.

2.5 受火后受剪承载力计算公式

2.5.1 单剪模型承载力

节点采用薄钢板连接件(即钢板厚度小于等于0.5def)时，其受火后单剪承载力计算公式为

(26)

式中，My应考虑受火后钢材的力学特性折减.

节点采用厚钢板连接件(钢板厚度等于大于def)时，其受火后单剪承载力计算公式为

(27)

节点采用厚度介于薄板与厚板之间的连接件时，其受火后单剪承载力应在薄板与厚板的承载力之间采用线性插值法计算得到.

2.5.2 自攻螺钉群效应

对于垂直钉入CLT层板的多个自攻螺钉，认为其有效个数nef与实际个数相同，即总的受剪承载力Fv,ef等于各个单剪紧固件承载力之和[5].

2.6 算例验证

基于实测炭化深度，采用2.5节方法计算试件受火后受剪承载力.由于试件采用的钢板厚度介于0.5def～def之间，应采用式(26)和(27)分别计算薄钢板和厚钢板的受火后单剪承载力.按薄钢板计算时，节点发生侧构件单个塑性铰屈服；按厚钢板计算时，节点发生双塑性铰屈服.试件受火后受剪承载力通过对单剪承载力按钢板厚度进行线性插值，并乘以nef得到，相应计算结果列于表5中.

由表5可知，R60组与R80组试件受剪承载力计算值与试验值的相对误差不超过7.6%，证明该计算方法具有较好的精度.此外，2组计算值相同，说明自攻螺钉长度的增加对受火后受剪承载力基本无影响，与试验结果一致.究其原因在于，2组试件的非持力层厚度、屈服弯矩、等效直径及销槽承压强度基本相同，仅等效销槽承压长度不同.由式(17)、(24)和(25)可知，当发生侧构件单个塑性铰屈服和双塑性铰屈服时，等效销槽承压长度不影响理论屈服承载力，仅影响绳索效应承载力提高项.但由于2组试件的绳索效应提供的承载力超出了理论屈服承载力，绳索效应承载力提高项最终根据理论屈服承载力进行取值，从而导致2组试件的受剪承载力计算值相同.

表5 试件受火后的受剪承载力计算值与试验值对比

实际工程中，利用实测炭化深度计算受剪承载力不具操作性，因此应采用式(1)计算炭化深度.在炭化深度实测值与计算值吻合良好的前提条件下，重新采用炭化深度计算值来计算受剪承载力，并与试验值进行对比，结果见表6.

表6 基于炭化深度计算值的试件受剪承载力计算值与试验值对比

由表6可知，R60组与R80组试件的受剪承载力计算值与试验值的误差不超过6.3%，计算精度较高，故建议采用炭化深度计算值计算节点受火后受剪承载力.

3 结论

1)将自攻螺钉长度由60 mm增至80 mm，节点的常温屈服荷载升为原来的1.51倍，延性系数降为原来的0.77倍.受火20 min后，对于自攻螺钉长度分别为60和80 mm的节点，屈服荷载分别降低73%和81%，延性系数分别提高5%和38%.

2) 试验结果和计算结果说明，靠提升自攻螺钉长度的方法来提高受火后受剪承载力是基本无效的.究其原因在于，试件受火后易发生侧构件塑性铰屈服及双塑性铰屈服，这2类屈服模式的承载力与自攻螺钉长度无关.

3) 与常温CLT层板销轴类紧固件常温受剪承载力计算方法相比，本文提出的节点受火后受剪承载力计算方法考虑了自攻螺钉抗弯强度的折减以及受火后CLT层板的炭化层和零强度层的承载失效.采用本文方法计算得到的受火后受剪承载力误差不超过7.6%，与试验结果较为吻合，从而验证了该方法的正确性与适用性.

4) 由NDS2018得到的炭化深度计算值与实测炭化深度吻合较好，基于该炭化深度计算节点受火后受剪承载力时计算值与试验值的误差不超过6.3%，故建议在承载力计算中采用计算炭化深度代替实测炭化深度.