非饱和弱膨胀土土-水特征曲线拟合与渗透系数模型预测

丁小刚，余云燕，蔺文博，金依蕊

(兰州交通大学土木工程学院，甘肃兰州，730070)

兰新(兰州—乌鲁木齐)高速铁路的建成运营为我国西部地区经济核心区的形成及“丝绸之路经济带”的构建奠定了坚实基础，该线路沿线(新疆哈密段)在联调联试前期出现多处地基膨胀上拱病害，查阅原地勘及设计资料和试验取样分析发现，该地区膨胀土系典型侏罗系沉积岩，含微量蒙脱石等强亲水性黏土矿物，具有胀缩性、裂隙性和超固结性等膨胀特性[1]，水环境的改变往往引起膨胀土的干缩或湿胀，决定膨胀土路基的变形程度，影响线路的安全运营。水分在非饱和土中的迁移使得土体的渗透性、膨胀性呈现动态变化[2]，量测非饱和膨胀泥岩的土水特性、渗透特性，可以将泥岩的膨胀特性与渗透特性相互联系起来以评估地基的服役状态。因此，有必要对该地区膨胀土的土水特性及渗透特性进行相关研究。

土的骨架变形规律和流体的流动规律构成了非饱和土力学的基本框架[3]，土骨架系统包括固相和气液交界面(收缩膜)。为研究土骨架结构的改变对土水特性的影响，张唐瑜等[4-5]通过压汞试验及扫描电镜试验探究了压实作用对膨胀土微观孔隙结构的影响，李同录等[6-8]分析了孔隙结构的改变对土水特征曲线的影响。吸力的变化体现在土体的强度特征，反映于土体骨架结构，而流体系统中的气相和骨架间的相互作用使得土体的非饱和土渗透特性复杂化。考虑到直接测量土体的渗透系数对实验条件要求高，且耗时费力，多数学者采用间接方法计算得到土体的非饱和渗透系数，其中，由CHILDS 等[9]基于孔隙分布函数和Darcy定律提出的Childs &Collis-George 模型(CCG 模型)，由将Brooks-Corey 土水特征曲线模型代入Burdine 模型建立的BCB 模型和将土水特征曲线VG 模型代入Mualem 模型建立的VGB 模型[10-11]以及陶-孔模型[12]，均可对非饱和土的渗透系数进行预测。其中，CCG 模型在膨胀土领域应用广泛[13-14]，在取得土水特征曲线的基础上分别采用Childs&Collis-Geroge模型求得不同地区非饱和膨胀土的渗透系数、含水率、基质吸力的关系，预估不同性质膨胀土的非饱和渗透系数发展规律。然而，地区差异对土体非饱和特性影响不可忽略，且鲜有考虑压实作用引起的土骨架变形对其非饱和渗透特性的影响，因此，有必要针对具体特定地区的土体非饱和特性进行研究。

针对上述问题，本文作者采用压力板仪(0～0.5 MPa)和滤纸法(0.01～40 MPa)试验进行土-水特征曲线试验，基于压汞试验测试压实作用对新疆哈密地区重塑弱膨胀土孔隙结构的影响，采用室内变水头法试验测定土体饱和渗透系数发展规律，并基于Fredlund &Xing 模型[15]和Childs &Collis-Geroge模型[9]对非饱和重塑弱膨胀土的渗透系数进行预测，并结合不同地区膨胀土CCG 模型渗透系数进行对比分析，以探究孔隙结构、孔隙分布的改变对土-水特征曲线及土体饱和渗透系数的影响及其发展规律。

1 试验土样

试验土样取自新疆哈密地区沿线上拱病害地段，采用钻机钻芯取样，取样深度为8～13 m，系典型侏罗系沉积岩，呈泥状结构，泥质胶结，遇水易软化崩解，其基本特性见表1。该区毗邻天山山脉，主要水源为雪山融水，由附近植被及地下水渗出情况可知，该地带有丰富的地下水源。

表1 膨胀土试样基本物理力学指标Table 1 Basic physical and physical indicators of expansive soil samples

2 试验过程

2.1 压力板法试验

试验采用美国GCTS 所产SWCC-150 Fredlund土水特征压力仪，该压力仪由垂直气动加载装置、压力板仪组件、控制面板和水体积测量系统4部分组成。

使用液压千斤顶制取初始干密度分别为1.4，1.6 和1.8 g/cm3的环刀样，试验选用进气值为500 kPa 的陶土板，试验开始前，分别对陶土板和环刀试样进行浸水饱和，再进行逐级加压排水试验。吸力路径为20 kPa→40 kPa→60 kPa→80 kPa→100 kPa→200 kPa→400 kPa，期间不间断读数。每次读数前用洗耳球排空气泡，并于两侧水体变管稳定后进行下级加压，每级吸力平衡需10 d左右。

2.2 滤纸法试验

滤纸法试验遵循热力学平衡原理，其采用滤纸和环刀样直接接触法，通过滤纸与土体在水分传递上达到平衡测量基质吸力；非接触试验方法能够通过滤纸与空气中的水分达到平衡测量总吸力。试验原理图如图1所示。

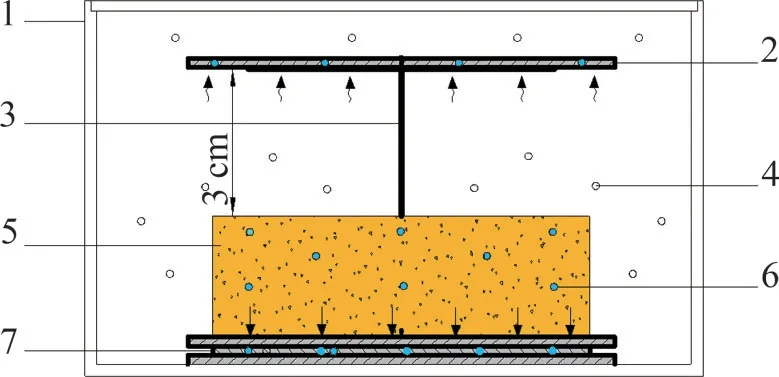
图1 滤纸法试验原理示意图Fig.1 Schematic diagram of principle of filter paper test

采用国产“双圈”牌No.203 型慢速滤纸测量基质吸力，由下列滤定曲线方程[16]进行分析：

式中：ψ为土体基质吸力，kPa；wfp为滤纸质量含水率，%。

试验步骤如下：

1)将“双圈”滤纸置于烘箱烘干12 h备用。

2)将土样碾细并过2 mm筛，置于恒温烘箱恒温105 ℃烘干8 h。

3)使用环刀制样器和液压千斤顶制备初始干密度分别为1.4，1.6 和1.8 g/cm3的3 组直径为61.8 mm、高为20 mm 的环刀样，以4%含水率为初始含水率，2%含水率为梯度，配制10组不同含水率的土样，并制备平行试样。

4)试验采用圆形密封盒作为试验容器，在盒底放置3张滤纸，其中两侧滤纸为保护滤纸，其直径略大于环刀直径；中间滤纸为接触法测量滤纸，其直径同环刀直径。

5)使用配套的密封垫圈进行密封处理并置于恒温25～27 ℃的试验箱中平衡10 d。

6)采用精度为0.000 1g的电子天平迅速测量滤纸含水率。

2.3 压汞试验

压汞法(mercury intrusion porosimetry,MIP)是基于水银对固体表面的不可湿润性，假设多孔材料是由大小各异的圆筒型毛细管构成，根据毛细管内液体升降原理量测材料的微观孔结构。根据WASHBURN 方程[17]得到水银所受压力p和毛细管半径R的关系如下：

式中：p为压入水银压力，N·m2；σ为水银的表面张力，取σ=0.485 N/m；α为所测多孔材料与水银的湿润角，试验取α=130°；R为毛细管半径，m。

试验分别制作初始干密度为1.4，1.6和1.8 g/cm3的3组重塑土样，采用冷冻干燥法干燥试样。

2.4 饱和渗透试验

饱和渗透系数试验采用TST-55渗透仪变水头法进行测定，依据TB10102—2010“铁路工程土工试验规程”进行试验。分别制作初始干密度(ρd)为1.4，1.5，1.6，1.7和1.8 g/cm3的5组重塑土样，并制备平行试样，试验结果取均值。

3 结果分析和评价

3.1 土-水特征曲线

采用压力板试验(吸力范围为0～0.50 MPa)和滤纸法试验(吸力范围为0.01～40.00 MPa)得到不同初始干密度(ρd)下新疆非饱和弱膨胀土的土-水特征曲线(SWCC)，如图2所示。由图2可知：在不同初始干密度下，膨胀土土-水特征曲线均近似呈“S”形，在相同初始干密度下，膨胀土基质吸力均随体积含水率增加而呈非线性减小；而在相同体积含水率下，膨胀土基质吸力随初始干密度增加而呈现不同程度的增加。

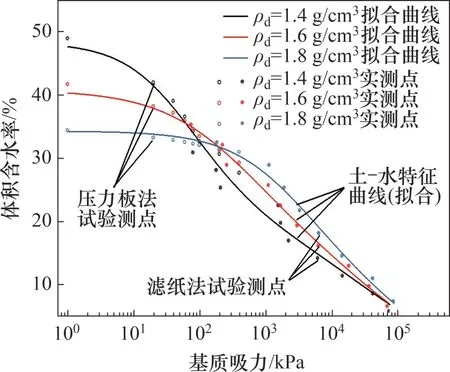
图2 新疆非饱和弱膨胀土的土-水特征曲线Fig.2 Soil-water characteristic curves of Xinjiang unsaturated weakly expansive soil

为得到不同初始干密度对新疆非饱和弱膨胀土基质吸力和土-水特征曲线发展规律的影响，分别采用3种典型SWCC模型(Van Genuchten模型(VG 模型)、Fredlund &Xing 模型(F-X 模型)(见式(3)和(4))和Gardner 模型)，对试验所得不同初始干密度下基质吸力与体积含水率的土水-特征曲线进行拟合。经拟合发现，Fredlund &Xing 模型的拟合系数R2均达到0.980 以上，其拟合效果比V-G 和Gardner 模型的优，更适用于新疆非饱和弱膨胀土吸力拟合分析，其拟合参数如表2所示。

表2 F-X模型拟合SWCC参数Table 2 F-X model fitting SWCC parameters

1)Fredlund&Xing模型：

式中：θ为体积含水率，%；θs为饱和体积含水率，%；C(ψ)为修正函数；Cr为残余基质吸力，kPa；e为自然对数常数，取2.718 28；a，m和n为拟合参数。

2)Van Genuchten模型：

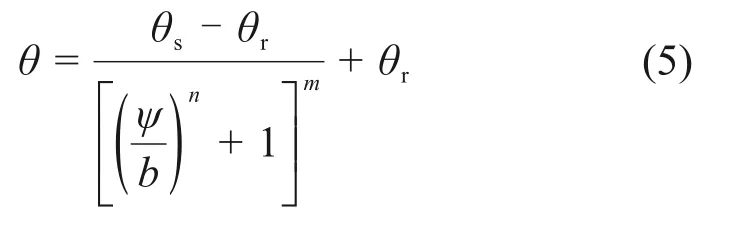
式中：b，m，n为拟合参数，m=1-1/n。

3)Gardner模型：

3.2 孔径分布曲线

由压汞试验得到孔隙直径与累计汞压入体积关系，绘制3组不同初始干密度下新疆非饱和弱膨胀土的孔径分布曲线(pore size distribution,PSD)，如图3所示。

压汞法孔径分布曲线反映不同压实程度下膨胀土微观孔径分布规律。由图3可知：试样的孔隙直径分布在6～106nm 之间，膨胀土孔径分布曲线呈初始三峰状分布并逐渐趋于双峰状过渡，对应的孔径范围分别为6～77 nm(峰Ⅰ)、550～3 900 nm(峰Ⅱ)和6 800～91 683 nm(峰Ⅲ)。随压实程度增加，中、小孔隙部分孔隙分布曲线峰值和峰宽波动较小，大孔隙部分峰值降幅显著且明显左移，峰宽略有减小，孔径分布曲线逐渐趋于双峰状。

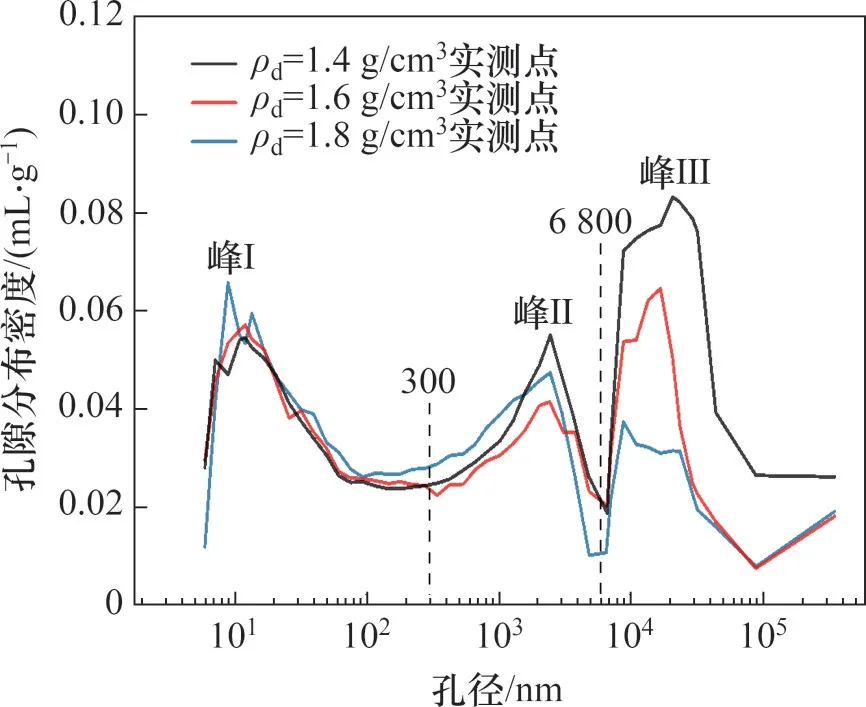
图3 新疆非饱和弱膨胀土的孔径分布曲线Fig.3 Pore size distribution curves of unsaturated weakly expansive soil in Xinjiang

参照张英等[18]对孔径的分类方法，将孔径(d)划分为小孔(6＜d≤300 nm)、中孔(300＜d≤6 800 nm)和大孔(d＞6 800 nm)。按划分的孔径分别进行不同区间孔隙体积统计，如图4所示，得到压实作用使得土体内部孔隙总体积累计减少量为28.09%，大、中和小孔隙总体积累计减少量分别为60.00%，12.36%和-3.16%，且小孔隙体积分数呈增加趋势，压实作用对膨胀土孔隙分布、孔隙体积及体积分数影响显著。

图4 初始干密度对孔隙体积影响Fig.4 Influence of initial dry density on pore content

3.3 饱和渗透系数

变水头渗透试验渗透系数参照试验依据TB10102—2010“铁路工程土工试验规程”进行，测得渗透仪出水口处水温为18 ℃。实验以20 ℃为标准温度，水的动力黏度比(ηt/η20)取值为1.050。得到重塑弱膨胀土饱和渗透系数计算结果如表3所示。

表3 饱和弱膨胀土渗透仪系数ks测试结果Table 3 Saturated permeabilities of loess in tests

为分析初始干密度对饱和渗透系数的影响，基于最小二乘法对试验数据进行拟合，如图5所示。

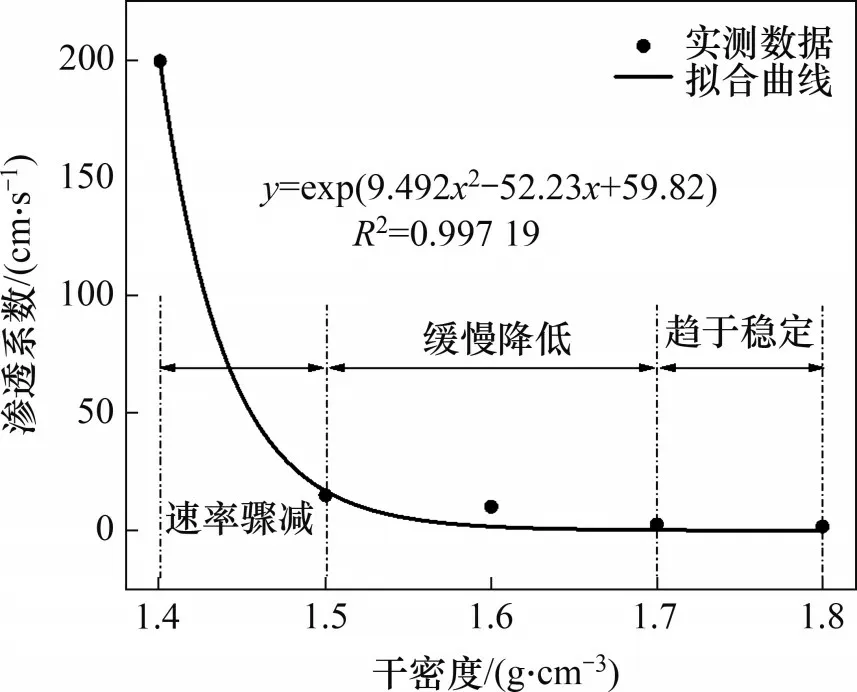
图5 饱和渗透系数与干密度关系Fig.5 Relationship between saturated permeability coefficient and dry density

从图5可知：重塑弱膨胀土的饱和渗透系数随初始干密度增加而呈现非线性降低趋势；在初始干密度为1.4～1.5 g/cm3之间时，重塑土渗透系数快速下降；在初始干密度大于1.5 g/cm3时，重塑土渗透系数缓慢减小，尤其是在1.7～1.8 g/cm3之间时重塑土渗透系数变化很小，趋于稳定，即膨胀土的饱和渗透系数经历渗透系数骤减、缓慢降低和趋于稳定3个阶段。

3.4 土体孔隙结构对土-水特性的影响

结合土-水特征曲线(图2)和孔隙分布曲线(图3)可知：重塑非饱和弱膨胀土的土-水特征曲线符合孔隙分布曲线三峰态分布规律，半对数坐标下SWCC 走势呈台阶状，结果与PSD 曲线三峰状分布相符合。土的土-水特性受孔隙分布控制，膨胀土基质吸力均随体积含水率增加而呈非线性减小，随压实程度增加而呈现不同程度增加。结合PSD曲线可认为：当初始干密度较小时，土颗粒之间的孔隙较发育，大孔隙体积占比大；随初始干密度增加，土骨架被破坏，压实、重组甚至填充，大孔隙体积减小，小孔隙数量增加明显且土体总孔隙数量增加，因此，土体基质吸力增加。

结合试样孔隙结构特点和饱和渗透系数发展规律(图5)可知：随着初始干密度增加，峰Ⅲ的峰值、峰宽降幅明显，试样中部分大孔隙被破坏、压实、填充密实或转化成其他更小直径的孔隙，总孔隙、大孔隙体积明显减小。土体渗流主要依靠连通的大孔隙，因此，土体饱和渗透系数随之减小；当土体初始干密度较大、孔隙体积趋于稳定时，再增大初始干密度、减小孔隙比，饱和膨胀土的渗透系数变化不大。

4 非饱和弱膨胀土渗透系数预测

当土体中同时存在水、气两相时，气相对水相的运动将产生阻滞或推动作用，使得非饱和土中水相渗透规律较饱和土更为复杂和多变。渗透系数取决于土体的体积含水率θ，θ反映于土体吸力ψ，ψ受土体微观孔隙结构的控制。CHILDS等[9]利用充水孔隙空间的形状提出了预测渗透系数的Childs &Collis-Geroge 模型，该模型被KUNZE等[19]进行了多次修改，结合土水特征曲线Fredlund&Xing 拟合模型，建立任意孔径分布基础上的非饱和土渗透系数预测模型，将利用F-X模型得到的土水特征曲线沿体积含水率轴等分为N份，以每份中点的基质吸力计算相对渗透系数kr(ψ)。

某一特定体积含水率下的渗透系数k(θi)是将相应于θi及低于θi的体积含水率的基质吸力求和。相对渗透系数的积分形式为

式中：kr(θ)为相对渗透系数；θL为最低容积体积含水率。

若任意土体吸力ψ所对应的渗透系数是以饱和渗透系数ks为参考，则渗透系数k(ψ)为

对于所有种类的土体而言，与零含水率对应的总吸力本质是相同的，且该值约为106 kPa，并且通过各种土壤的试验和热动力学研究得到了试验验证。Fredlund＆Xing 提出了一个描述整个吸力范围(0～106 kPa)内的土-水特征曲线的一般方程式(见式(3))，因此，基于F-X土-水特征曲线模型，结合修正的Childs&Collis-Geroge模型可得到土体相对渗透系数表达式如下：

式中：b1=ln(106)；ψaev为进气值；y为吸力对数的积分虚拟变量；θ′为式(3)的导数。

式(9)可采用数值积分方法来计算，假设a1和b1分别为积分的上、下限，则

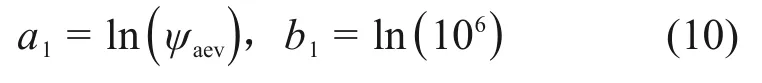
将[a1,b1]等分成N段，用Δy表示分段的长度，则

对于在进气值ψaev和106 kPa 之间的任何吸力ψ，ln(ψ)均介于a1和b1之间。假定ln(ψ)在第j个区间[yi,yi+1]中，则式(9)可以简化为

式中：yi为第i个区间[yi,yi+1]的中点；ln(ψ)对应于第j个区间[yj,yj+1]。

根据Childs&Collis-Geroge 模型，结合土-水特征曲线F-X模型，将土水特征曲线按体积含水率分为20 等分，并将各等分中点对应的基质吸力代入式(13)，计算得到非饱和渗透系数k(ψ)，见表4。

表4 新疆非饱和重塑弱膨胀土渗透系数Table 4 Permeability coefficient of unsaturated remolded weak expansive soil in Xinjiang

通过弱膨胀土的土-水特征曲线，建立非饱和渗透系数与体积含水率、基质吸力的关系如图6所示，并对渗透规律进行拟合分析，得到初始干密度 分 别 为1.4，1.6 和1.8 g/cm3时lgk(ψ)-θ和lgk(ψ)-ψ的对应关系，如式(14)～(19)所示。

图6 不同初始干密度下新疆非饱和弱膨胀土渗透系数Fig.6 Unsaturated permeability coefficient of weak expansion soil in Xinjiang at different initial dry densities

当初始干密度为1.4 g/cm3时，

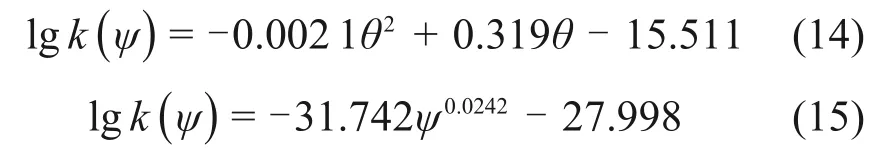
当初始干密度为1.6 g/cm3时，

当初始干密度为1.8 g/cm3时，

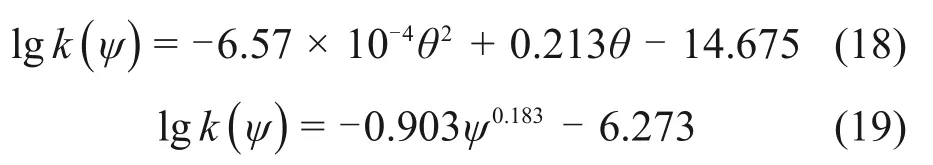
由图6可知：lgk(ψ)与基质吸力和含水率的关系可分别通过二次多项式和指数函数形式表示，R2均大于0.98，拟合关系显著。结合表4中渗透系数与体积含水率的关系可知：土体的渗透性参数随吸力或含水率增加而呈非线性变化，重塑膨胀土的渗透系数随初始干密度增加而降低，随岩土体基质吸力增加而减小，随含水率增大而增加。

非饱和土中水体流动主要是重力水(或弱结合水)参与，水的流动均受重力作用控制。对于不同粒径的非饱和土体，在减饱和过程中，相同吸力增量的大孔隙优势土层所能排出水的体积远比小孔隙优势土层的大。结合图2中孔隙分布曲线可知，压实作用使得土中峰Ⅲ(大孔径孔隙)体积累计降低60%，且土体原本连通的大孔隙被不断破坏、填充或转化为更小直径的孔隙，孔隙间连通性降低，因此，随初始干密度增加，土颗粒间孔隙被进一步压缩、填充，大孔隙体积减小，孔隙间连通性下降，小孔隙优势增加，在相同吸力增量下，土体排水能力降低，土体渗透系数减小。

5 不同地区膨胀土CCG 模型预测结果对比分析

许多学者采用Childs&Collis-Geroge对不同地区膨胀土渗透系数进行了计算分析，分别考虑初始干密度和土体膨胀能力差异对非饱和土渗透系数发展规律的影响，本文选取文献[13,20-21]中典型Childs&Collis-Geroge 模型结果进行对比分析，如图7所示。

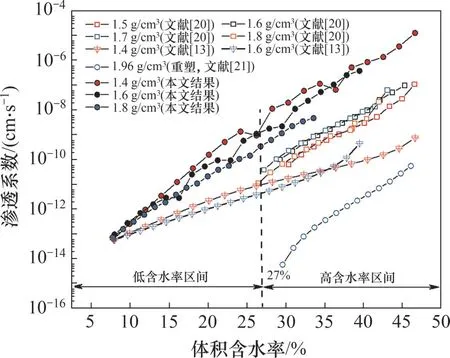
图7 不同地区膨胀土CCG模型预测对比Fig.7 Comparison of CCG model predictions for expansivesoils in different regions

为提高渗透系数计算结果的准确性，采用压力板试验(0～0.5 MPa)和滤纸法试验(0.01～40 MPa)对新疆哈密地区高速铁路弱膨胀土分别测量低、高吸力范围的土-水特征曲线，并基于Fredlund&Xing 和CCG 模型得到不同初始干密度下的重塑弱膨胀土非饱和渗透规律。由图7可知：该地区非饱和弱膨胀土的渗透系数随基质吸力增大(体积含水率降低)而呈现非线性减小趋势；在相同体积含水率下，土体渗透系数随初始干密度增大而减小；在不同初始干密度下，渗透系数发展趋势(曲线斜率)基本一致，且相邻两干密度间隔内渗透系数曲线波动在1个数量级内。

贺雷等[20-21]通过压力板法试验，分别对湖北宜昌和广西宁明地区重塑弱膨胀土低吸力范围(0～0.5 MPa)土-水特征曲线进行测试，并基于Van Genuchten 模型和CCG模型得到不同初始干密度下的重塑弱膨胀土非饱和渗透系数。由图7还可知：湖北宜昌地区弱膨胀土渗透系数受土体初始干密度影响较小，且不同初始干密度下渗透系数发展趋势(曲线斜率)基本一致；广西宁明地区初始干密度为1.96 g/cm3的弱膨胀土渗透系数均小于本文结果(新疆哈密地区)和湖北宜昌地区中干密度为1.8 g/cm3的渗透系数，半对数坐标中曲线位置更低，且该渗透系数曲线发展趋势(曲线斜率)与新疆、湖北地区中的基本一致。戴张俊等[13]借助陶土板进气值为1.5 MPa的压力板仪，通过水体积变化系数的变化规律，得到河北地区非饱和中膨胀土的渗透系数发展规律。由图7可知：该地区土体体积含水率小于10%时，土体渗透系数接近本文同条件下土体的渗透系数，随体积含水率增加，渗透性曲线逐渐靠近干密度更大的土体渗透性曲线；在半对数坐标下，文献[13]中，中膨胀性土体各初始干密度下试样的渗透性曲线斜率均小于弱膨胀土曲线斜率，并基于此推断强膨胀性土体渗透性曲线斜率小于中或弱膨胀土曲线斜率，与文献[13]中结论相符合。

为探究土体渗透特征与其初始干密度和土体膨胀潜势的关系，采用控制变量原理分别对两因素影响下的土体渗透系数进行对比分析，结合本文土体孔隙结构分析可知：在相同膨胀潜势、不同初始干密度下，压实作用使得土体孔隙总体积减小，大孔隙数量降低，小孔隙占比增加，孔隙间连通性降低，使得在相同基质吸力下，随着土体初始干密度越大，土体进气值越大，非饱和渗透系数越小，土体表现出更好的持水性能，且不同地区土体性质差异等因素的影响使得相同密度状态下渗透系数存在一定程度的波动；在相同初始干密度、不同膨胀潜势下，半对数坐标下渗透系数曲线斜率均小于相同初始干密度下弱膨胀土体曲线斜率，其原因为土体次生黏粒矿物(蒙脱石、伊利石和高岭石)含量的差异使得中膨胀性土体在吸湿过程中体积变化比弱膨胀性土体更剧烈，土体内部大孔隙被不断压缩、破坏甚至填充，大孔隙体积减少，孔隙连通性逐渐降低，因此，在相同初始干密度条件下，其渗透系数比弱膨胀土增长更缓慢，土体持水性能更好。

6 结论

1)膨胀土孔径分布曲线基本呈三峰状分布，随初始干密度增加，膨胀土总孔隙体积减少约28.09%，中、小孔隙体积维持稳定，占比增加，大孔隙体积明显减小，膨胀土孔径分布曲线逐渐趋于双峰状分布。

2)利用压力板仪、滤纸法试验测得膨胀土0～40 MPa吸力范围的土-水特征曲线，基质吸力随含水率增加呈非线性减小趋势，随初始干密度增大，土体进气值与残余基质吸力均增大。

3)非饱和重塑弱膨胀土渗透系数与土体孔隙结构、体积含水率和基质吸力均有密切关系。随初始干密度的增大，土骨架结构发生变化，大孔隙体积降低，孔隙连通性下降，小孔隙体积增加，土体吸力增大，渗透系数减小。对于膨胀土，吸湿膨胀亦会导致土骨架压缩变形，引起吸力和渗透系数增减。

4)土体非饱和渗透系数受干密度和膨胀潜势的共同影响，初始干密度越大，土体密实程度越高，孔隙结构越紧密，渗透系数越小；膨胀潜势越强，土体渗透曲线斜率越小，土体持水性能越好。