基于状态反馈解耦控制的含DFIG电力系统低频振荡抑制研究
于淼,李京霖
(1.北京建筑大学机电与车辆工程学院,北京 100044;2.北京市建筑安全监测工程技术研究中心,北京 100044;3.清华大学电力系统及发电设备安全控制和仿真国家重点实验室,北京 100084)
0 引言
国内外学者对风电并网低频振荡进行了深入研究。文献[1]提出一种均值方差映射算法进行控制器参数协调优化,可有效提高系统的区域阻尼并改善动态性能。文献[2]建立了考虑锁相环与虚拟惯量控制的双馈风电机组并网互联系统小干扰模型,采用解析方法从机理上分析锁相环与虚拟惯量共同作用下系统的小干扰稳定性。文献[3]提出了基于离散线性二次调节器(LQR)和基于卡尔曼滤波的状态估计的广域阻尼控制(WADC)方法,应用于区域间实时阻尼风力综合电网振荡,该算法可有效衰减区域间模态。文献[4]针对系统模型辨识误差因素进行了模型建模和阻尼控制器设计,基于递推最小二乘法与Vinnicombe距离理论,提出一种迭代辨识方法的阻尼控制器设计,能有效地抑制风电接入系统的低频振荡。文献[5]使用中心频率法、测试信号法,设计了电力系统稳定器(PSS)和附加直流功率调制器(DCM)。文献[6]对DFIG静态同步补偿器-静态同步串联补偿器(STATCOM-SSSC)和转子侧变换器进行协调设计,使得转子侧变换器(RSC)通过开关控制DFIG有功功率和无功功率。文献[7]利用功率振荡阻尼联合可控性和可观测性的最大概率值,确定WADC下电力在任意工作点的最佳输入和输出,提出的自适应控制器很好地保持了风电系统预期的鲁棒性和阻尼性能。文献[8]针对典型风电电压源型并网变流器提出一种频率耦合阻抗模型,考虑互补频率耦合效应和外环控制,进一步构建并网系统的整体阻抗模型。文献[9]提出一种鲸鱼优化算法(WOA),对目标函数进行改进来调整控制器的变量,采用模态可观测性确定合适功率阻尼振荡器输入信号,从而在风电系统中获得较好的低频振荡控制效果。文献[10]提出一种在DFIG和弱电网之间阻尼控制策略,利用区域极点配置混合H2/H∞控制抑制低频振荡。
利用凸多面体的不同工作点作为凸多面体的顶点,确保在更大工作范围内的适用性,使得系统允许保持良好的阻尼性能。在风机存在不确定性的情况下,可补偿DFIG的无功功率,提高系统振荡阻尼。文献[11]提出在DFIG中配置电力系统稳定器(PSS),改善风电系统阻尼。文献[12]提出一种基于矢量裕度法的风电并网电力系统低频振荡分析方法,该方法可以计算多台DFIG同时接入电网时,各自对系统低频振荡模式的影响,并通过二维复平面图示化分析使得结果更加清晰直观。文献[13]提出一种基于自抗扰控制器的广域阻尼控制器协调优化策略,利用人工蜂群算法对自抗扰控制器和广域阻尼控制器进行协调优化,以增强系统的稳定性。文献[14]提出一种基于凸多面体的鲁棒阻尼控制器,不仅能够为系统次同步振荡模式提供足够的阻尼,而且风电功率在较大范围内变化的情况下,控制器也具有较好的控制效果。文献[15]提出了频率阻尼控制方案,在转子电流环中加入利用锁相环获得的频率作为控制信号,明显抑制弱电网DFIG低压穿越期间的系统振荡,提高系统阻尼比,改善了系统小信号稳定性。
上述研究没有考虑DFIG接入电网引起电力系统角速度偏差变化、功角变化、阻抗变化以及三者之间的耦合作用对低频振荡的影响。因此,本文根据已有的闭环电力系统状态空间模型,提出将DFIG视为一个单输入双输出的反馈控制器,对其传递函数进行状态反馈解耦控制,通过在DFIG中引入输入变换阵F和状态反馈阵K,使得反馈控制器传递函数阵变为非奇异对角矩阵,实现对同步发电机注入DFIG的变量的一对一控制。然后根据耦合系数与阻尼比之间的关系,通过改变阻尼比进而抑制低频振荡,保证电力系统稳定性。
1 系统模型
1.1 电力系统状态空间模型

电力系统稳态运行时,DFIG向电力系统注入的有功功率和无功功率如图1所示。

图1 含DFIG的电力系统Fig.1 Power system with DFIG
图中:Pω+j Qω=Pω0+j Qω0+ΔPω+jΔQω,其中ΔPω,ΔQω分别为DFIG注入电力系统之间的有功功率和无功功率变化。
选择Pω和Qω作为DFIG到电力系统的控制信号,建立不含DFIG电力系统状态空间模型[18]。

式中:Δδ,Δω分别为同步发电机功角、角速度的偏差矢量;ΔZ为从同步发电机到电力系统中其他状态变量矢量;bP2,bP3,bQ2,bQ3分别为与有功功率和无功功率有关的控制向量;Cg1,Cg2,Cg3分别为功角、角速度和阻抗的耦合参数;dg1,dg2分别为有功功率和无功功率变化反馈参数;ΔVω为风电机公共连接点处的电压幅值偏差。
1.2 含DFIG电力系统闭环模型

DFIG响应随公共节点电压ΔVω变化,在电力系统中,通常限制由ΔVω引起DFIG的动态响应。因此DFIG引入的动态交互作用将会受到限制。式(2),(4)共同构成含DFIG电力系统闭环控制模型,如图2所示。

图2 含DFIG电力系统闭环控制模型Fig.2 Closed-loop control model of power system with DFIG
2 基于状态反馈解耦方法
2.1 状态反馈解耦
状态反馈解耦可实现系统一对一控制,保证了各单入单出系统单独运行,实现对解耦变量的单独控制[24]。本文主要通过解耦方法对DFIG并网带来的多变量耦合作用系统进行一对一控制,从而实现一个多入多出系统解耦的充要条件,即系统的传递函数矩阵能化为对角矩阵。
对角阵的转换通常利用状态反馈加输入变换阵的结构形式,状态反馈解耦控制的状态空间结构如图3所示。图中:K为状态反馈阵,为2×2阶常数阵;F为2×2阶输入变换阵[19]。
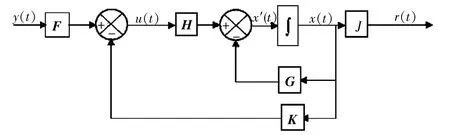
图3 状态反馈解耦控制状态空间结构图Fig.3 State space structure diagram of state feedback decoupling control



2.2 DFIG对阻尼转矩幅值的影响
电力系统产生的Δδ,Δω,ΔZ通过功角耦合参数Cg1、角速度耦合参数Cg2以及阻抗耦合参数Cg3耦合作用于PCC,它们会引起节点电压的变化[18],PCC电压幅值ΔVω的变化会引起DFIG输出功率幅值变化,进而影响阻尼力矩幅值变化,即电力系统的输入发生变化。在电力系统中,正常情况下ΔVω的动态变化是有限的,因此DFIG的动态响应也是有限的。
但是由于Δδ,Δω,ΔZ 3个偏差变量共同作用于PCC电压,这使ΔVω受到1~3个变量的影响,任何一个偏差变量超出峰值,都可能引起ΔVω的动态变化超出限制[22],这就可能导致系统发生低频振荡,产生不利后果。由DFIG输出功率可得到同步发电机机电振荡回路贡献的传递函数矩阵为

由式(12)可以看出,阻尼力矩与PCC节点电压ΔVω成正比。因此,可以通过应用阻尼力矩幅值(DTA)来分析DFIG引入对节点电压ΔVω幅值的影响[17],[18]。
2.3 基于状态反馈解耦控制方法
本文将DFIG视为一个单输入双输出的反馈控制器,提出对其传递函数阵GωP(s)和GωQ(s)进行状态反馈解耦控制,通过在DFIG中引入输入变换阵F和状态反馈阵K,使得DFIG传递函数阵变为非奇异对角矩阵,即可实现对Δδ,Δω,ΔZ的一对一控制。然后根据耦合系数Cg1,Cg2,Cg3与阻尼比之间的关系,调节耦合系数Cg1,Cg2,Cg3的数值,改变阻尼比进而抑制低频振荡,保证电力系统稳定性。具有DFIG并网的电力系统的闭环控制系统解耦模型如图4所示。图中:Fij(i=1,2;j=1,2)为输入变换阵F中的元素;Kij(i=1,2;j=1,2)为状态反馈阵K中的元素;Gij,Hij,Jij(i=1,2;j=1,2)为DFIG状态空间表达式系数矩阵中的元素。

图4 含DFIG电力系统的闭环控制系统解耦模型Fig.4 Decoupling model of closed-loop control system with DFIG power system
由图4可以分别写出阻尼力矩ΔT对Δδ,Δω,ΔZ整个系统闭环传递函数为φδ(s),φω(s),φZ(s)。然后将此传递函数模型进行模型降阶,降为二阶模型与其他阶次模型形式,以Δδ为例,假设其降阶后模型为

由式(14)可知,通过减小参数Cg1可以提高整个系统的阻尼比。同时,经仿真验证,减小Cg1值,还能降低Δδ变化对阻尼力矩幅值的影响。
2.4 基于状态反馈解耦控制设计步骤
本文基于状态反馈解耦控制提高阻尼比的具体流程如图5所示。

图5 基于状态反馈解耦控制提高阻尼比流程图Fig.5 Flow chart of improving damping ratio based on state feedback decoupling control
3 仿真验证
本文以风电接入四机两区域系统作为算例仿真进行验证,在Matlab/Simulink环境中建立仿真模型,如图6所示。

图6 风电接入四机两区域系统模型Fig.6 Four-machine and two-area of wind power system model
通过设置一个二阶传递函数进行模拟验证参数控制阻尼比,并同时降低阻尼力矩幅值变化效果。图中:区域1含有两台容量为900 MW同步发电机G1,G2和一台DFIG,DFIG经长距离输电线路接入母线6;区域2含有两台900 MW同步发电机组G3,G4和一台DFIG,DFIG经长距离输电线路接入母线10。具体参数设定如下。

参考DFIG阻尼特性[24],计算参数Cg1,Cg2,Cg3对应阻尼的数值如表1所示。
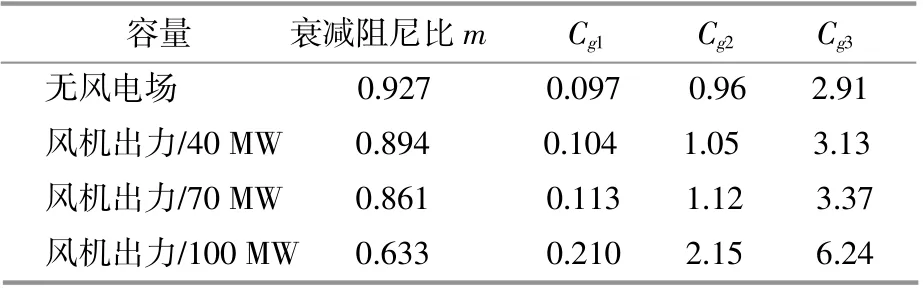
表1 不同风机出力条件下阻尼比对应C g1,C g2,C g3的数值Table 1 The values of damping ratio corresponding to Cg1,Cg2,Cg3 under different fan output conditions
系统阻尼比随参数Cg1,Cg2,Cg3变化仿真曲线如图7所示。

图7 阻尼比随C g1,C g2,C g3变化曲线Fig.7 Variation curve of damping ratio with Cg1,Cg2,Cg3
由图7可以看出,随着参数Cg1,Cg2,Cg3增大,系统阻尼减小,阻尼比与参数Cg1,Cg2,Cg3成反比。因此,可以通过减小参数的方式来提高系统阻尼比。
本文将Cg1,Cg2,Cg3代入仿真算例系统模型,并与传统状态观测器方法进行对比。
(1)Cg1和Cg2解耦后阻尼力矩幅值变化
基于本文提出的算法,再根据本节使用的算例,得出功角和角速度解耦后阻尼力矩幅值变化,如图8所示。

图8 功角和角速度解耦后阻尼力矩幅值变化Fig.8 Amplitude changes of the damping torque after decoupling of the power angle and frequency
由图8可知:在相同激励条件下,功角和角速度通过状态反馈解耦控制与传统状态观测器相比,对阻尼力矩振幅抑制明显;通过状态反馈解耦控制,使得Cg1作用下阻尼力矩振幅为[-0.007,0.172]N·m,Cg2作用下阻尼力矩振幅为[-0.053,0.612]N·m,而且振幅逐渐减小;而通过传统方法加入状态观测器,Cg1作用下阻尼力矩振幅约为[-0.221,0.588]N·m,Cg2作用下阻尼力矩振幅为[-0.401,0.731]N·m,而且振幅时常跳变。
因此,本文所述方法在功角和角速度作用于阻尼力矩幅值时,其振幅有所减小,而且逐步趋于稳定。
(2)Cg3和Cg1解耦后阻尼力矩幅值变化
基于本文提出的算法,再根据本节使用的算例,得出阻抗和功角解耦后阻尼力矩幅值变化,如图9所示。

图9 阻抗和功角解耦后阻尼力矩幅值变化Fig.9 Amplitude changes of the damping torque after decoupling of impedance and the power angle
由图9可知:在相同激励条件下,阻抗和功角通过状态反馈解耦控制与加入状态观测器相比抑制明显;状态反馈解耦控制使得Cg3作用下阻尼力矩振幅为[-0.60,0.62](N·m),Cg1作用下阻尼力矩振幅为[-0.13,0.36](N·m);而传统方法加入状态观测器,Cg3作用下阻尼力矩振幅为[-0.707,2.426](N·m),Cg1作用下阻尼力矩振幅为[-0.427,1.86](N·m)。两种方法虽然都未使阻尼力矩幅值趋于平稳,但状态反馈解耦方法对阻尼力矩振幅抑制作用更优越,而且幅值跳变明显小于传统方法。
(3)Cg2和Cg3解耦后阻尼力矩幅值变化
基于本文提出的算法,再根据本节使用的算例,得出角速度和阻抗解耦后阻尼力矩幅值变化图,如图10所示。

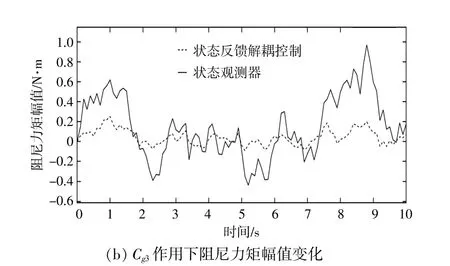
图10 角速度和阻抗解耦后阻尼力矩幅值变化Fig.10 Amplitude changes of the damping torque after decoupling of frequency and impedance
同样,由图10可知,在相同激励条件下,角速度和阻抗通过状态反馈解耦控制与加入状态观测器相比,状态反馈解耦控制作用对阻尼力矩振幅抑制更明显,作用结果与图9类似,不再赘述。
由图8~10可知,本文所提方法对阻尼力矩幅值抑制更强,式(11)已分析阻尼力矩与PCC节点电压ΔVω成正比,因此PCC节点电压ΔVω幅值得以抑制,从而可以保证含风电四机两区域间低频振荡控制稳定。
本文控制方法对低频振荡的功角和角速度抑制效果如图11所示。

图11 本文方法对低频振荡抑制效果Fig.11 Suppressing effects of low frequency oscillation by the method in this paper
由图11可知,使用本文方法后,同步发电机的功角和角速度幅值抑制效果显著,可以快速平息低频振荡现象。
4 结论
对含DFIG电力系统可能造成的区域低频振荡问题,本文提出一种基于状态反馈解耦控制的提高阻尼比方法,并给出算法设计流程。根据DFIG传递函数数学模型得出其状态空间表达式,并引入输入变换阵F和状态反馈阵K,将DFIG传递函数阵化为非奇异对角矩阵,将系统变为单输入单输出系统。在风电接入四机两区域上进行仿真验证,仿真结果表明,本文方法与传统状态观测器法相比,不仅能提高阻尼比,而且对功角Δδ、角速度Δω、阻抗偏差变量ΔZ变化引起的PCC节点电压ΔVω幅值变化抑制明显,ΔVω曲线逐步趋于平稳。因此,本文方法可以有效地改善含DFIG电力系统所引起的阻尼比衰减问题,同时实现对PCC节点电压ΔVω幅值抑制,可有效地抑制含DFIG电力系统低频振荡,为其他工程实践提供借鉴。

