关注建模过程 发展核心素养——以人教版数学教材“图形与几何”领域为例

浙江舟山绿城育华学校（316000） 洪 飞

数学模型是用数学语言概括地描述现实世界万事万物的特征、数量关系和空间形式的一种思维形式。在数学课堂中，教师要根据学生的思维特点，让他们像数学家那样进行探索和创造，关注学生对数学概念的建模过程，引导他们经历数学知识的具象和抽象过程，从而有效培养学生的模型意识，发展他们的核心素养。

一、模型意识在“图形与几何”领域中的应用

在认识图形的特征时，学生经历了以下的建模过程：先从实物模型中抽象出数学模型，再从数学模型中抽象出模型的本质属性。在人教版数学教材“图形与几何”领域渗透模型意识的教学，我们对内容进行梳理，具体如下（见表1）。

表1 人教版数学教材“图形与几何”领域渗透模型意识的内容

（续表）

从上表中可以看出，渗透模型意识是引导学生经历对数学知识的再创造和数学化的过程。教师要引导学生在动手操作和举例比较中概括出相应的数学模型，帮助学生沟通数学与生活之间的联系。

二、模型意识在“图形与几何”领域教学中的渗透

数学课堂中，教师要选择合适的内容渗透模型意识，既要让学生感受到数学模型可以用来解决一类数学问题，是数学应用的基本途径，又要让学生认识到生活中的许多问题都与数学有关，可以把生活问题转化为数学问题，用数学知识和数学模型解决实际生活中的问题。

1.创设生活情境，渗透模型意识

数学源于生活，用于生活，高于生活。在“图形与几何”领域教学中，教师可根据学生的实际生活，创设生活情境，引导学生通过观察发现蕴含其中的数学规律。这样不仅能降低学生数学学习的难度，还能让学生经历从生活原型中抽象出数学模型的全过程。

例如，教学人教版数学教材四年级下册《三角形的认识》后，教师设计了一节“一共要多少根火柴棒”的数学思维课。课堂上，教师先让学生观察，然后数一数摆一个三角形需要多少根火柴，再引导学生用字母表示三角形个数和火柴棒根数之间的数量关系，最后让学生用字母表示长方形个数和可坐人数之间的数量关系。

活动（1）：用字母表示三角形个数和火柴棒根数之间的数量关系（出示图1）

图1

①数一数：摆1个三角形需要多少根火柴棒？摆2个三角形需要多少根火柴棒？摆3个三角形需要多少根火柴棒？②想一想：摆n个三角形需要多少根火柴棒？

师：同学们，请你们先数一数摆1个、2个、3个三角形需要多少根火柴棒，再想一想摆n个三角形需要多少根火柴棒。

（学生先独立思考，再在小组里分享自己的思考过程）

师：谁来说一说，摆出题中这三个图形分别需要多少根火柴棒？

生1：摆1个三角形需要3根火柴棒，摆2个三角形需要5根火柴棒，摆3个三角形需要7根火柴棒。

师：那么，摆n个三角形需要多少根火柴棒呢？你能用含有n的字母表达式写一写吗？

生2：我发现摆1个三角形需要3根火柴棒，摆2个三角形需要5根火柴棒，摆3个三角形需要7根火柴棒，也就是多摆1个三角形需要2根火柴棒，所以摆n个三角形需要3+2×n根火柴棒。

生3：不对。因为n=1时，摆1个三角形就需要3+2×1=5（根）火柴棒了。因此，字母表达式里不能是n，应该换成n-1，即摆n个三角形需要3+2×（n-1）根火柴棒。

师：我们一起来验证一下。如果n=1时，摆1个三角形需要3+2×（1-1）=3（根）火柴棒；如果n=2时，摆2个三角形需要3+2×（2-1）=5（根）火柴棒……你们还能想出其他的数量关系吗？

生4：我发现摆1个三角形需要3根火柴棒，摆2个三角形需要3×2=6（根）火柴棒，但实际上合起来摆2个三角形却少了1根火柴棒；摆3个三角形需要3×3=9（根）火柴棒，但实际上合起来摆3个三角形却少了2根火柴棒，所以摆n个三角形需要3×n-（n-1）根火柴棒。

……

活动（2）：用字母表示长方形个数和可坐人数之间的数量关系

出示题目（见图2）：（1）每张长方形桌子坐4人，2张长方形桌子坐多少人？3张长方形桌子坐多少人？（2）想一想，n张长方形桌子坐多少人？

图2

师：同学们先独立思考，再小组交流。

生5：2张长方形桌子坐6人，3张长方形桌子坐8人。我发现每增加1张长方形桌子，就多坐2人，所以n张长方形桌子坐4+2×（n-1）人。

生6：我发现原本2张长方形桌子可以坐4×2=8（人），但是2张长方形桌子拼起来后却少坐2人；3张长方形桌子可以坐4×3=12（人），但是3张长方形桌子拼起来后却少坐4人，所以n张长方形桌子坐……

上述教学，教师先引导学生从实际生活中抽象出数学模型，从简单的1个三角形、2个三角形、3个三角形中直观地发现其中的数量关系；再根据数量关系中的共性建立数学模型。这个数学建模的过程，有助于培养学生的数感，使学生发现其中的数学规律和数学知识本质。

2.借助操作活动，渗透模型意识

荷兰数学家弗莱登塔尔提出数学教育的三原则，即现实原则、数学化原则和再创造原则；同时，他认为“学习数学唯一正确的方法就是再创造，由学生自己把所要学习的数学知识发现或者创造出来”。

例如，教学人教版数学教材六年级上册《圆的周长》一课时，为了探究圆的周长计算公式的由来，教师引导学生从最初的用线测量圆的周长，到发现圆的周长与圆的直径有关，最终发现π的存在。

活动（1）：测量圆的周长

师：（出示一个圆）同学们，你们知道圆的周长是指哪一部分吗？请同学们指一指。（学生指着圆的最外面一圈）如果想知道这个圆的周长，你们有什么办法？

生1：可以在圆上固定一个点，从这个点开始，让它沿着直尺滚动一圈，回到这个固定点，就是这个圆的周长。

生2：可以找来一把卷尺，先从圆上某个固定点开始，卷尺绕着圆上再回到这个固定点，就能读出这个圆的周长了。

生3：可以准备一根线和一把直尺，先用线绕着圆的一周，再把这段线拉直放到直尺上，就能测量出这段线的长度了，也就是这个圆的周长。

师：刚才同学们想出了多种不同的测量圆周长的方法，但是它们在测量中都会产生误差。大家想一想，有什么办法可以计算出圆的周长？

……

活动（2）：计算圆的周长

师：老师为每个小组准备了3个大小不同的圆，请你们先想办法测量出圆的周长，再计算出每个圆的周长除以直径的商，并把计算结果填写在表格（见表2）里。

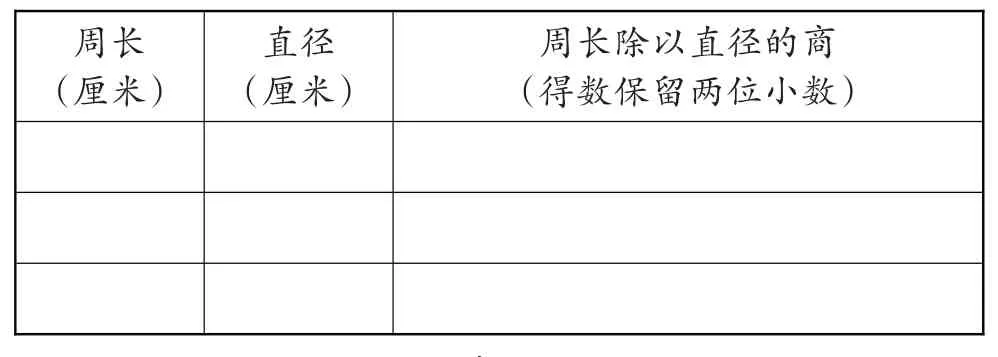
表2 圆的测量和计算探究

师：通过测量和计算，你们发现圆的周长和直径之间有什么关系？

生4：我发现圆的周长是直径的3倍多一点。

师：中国数学家祖冲之发现任何一个圆的周长除以直径的商都是一个固定值，叫作圆周率π。因此，圆的周长可以用C=πd或者C=2πr来计算。

……

上述教学，学生经历了测量圆的周长和计算圆的周长这两个过程。在动手动脑中，学生发现了圆的周长与直径之间的关系，自然地建立圆的周长公式模型。这样的探究活动，比教师的告知传授更能帮助学生理解圆的周长计算公式的由来。

3.借助猜想验证，渗透模型意识

数学课程标准要求学生会用数学的思维思考现实世界，形成重论据、有条理、合乎逻辑的思维品质，培养学生的科学态度与理性精神。猜想和验证是学生学习数学过程中应当具备的理性精神之一，所以教师在教学中应借助猜想和验证，向学生渗透模型意识。

例如，教学人教版数学五年级下册“表面涂色的正方体”时，教师先让学生猜测3面涂色、2面涂色、1面涂色和6面都不涂色的小正方体各有多少个，再让学生用n表示涂色小正方体的个数。

师：一个表面涂色的正方体，每条棱都平均分成2份，如果把它切开，能切成多少个同样大的小正方体？每个小正方体有几个面涂色？

生1：能切成2×2×2=8（个）同样大的小正方体，每个小正方体都有3个面涂色。

师：一个表面深色的正方体，每条棱都平均分成3份，如果把它切开，能切成3×3×3=27（个）同样大的小正方体，那么3面涂色、2面涂色、1面涂色的小正方体各有多少个？分别在什么位置？有6面都不涂色的小正方体吗？

（学生根据自己的思考猜测涂色的小正方体个数）

师：可以先把猜测的结果记录在学习单中，再验证自己的猜想。

生2：3面涂色的小正方体都在大正方体的顶点位置，一共有8个；2面涂色的小正方体都在大正方体每条棱的中间位置，一共有12个；1面涂色的小正方体都在大正方体每个面的中间位置，一共有6个。6面都不涂色的小正方体有27-8-12-6=1（个）。

师：一个表面深色的正方体，每条棱都平均分成4份，如果把它切开，能切成4×4×4=64（个）同样大的小正方体，那么3面涂色、2面涂色、1面涂色的小正方体各有多少个？分别在什么位置？

……

上述教学，面对较复杂的数学问题，教师带领学生经历了从猜想到验证的建模全过程，不仅教给学生数学学习的方法，还让他们感受到数学的严谨性和魅力。

三、模型意识在“图形与几何”领域中的价值

模型意识在“图形与几何”领域中有着较为广泛的应用，主要体现在以下两个方面。一是可让学生学会学习的方法。如果具备模型意识，学生就会在不重复的枚举中先数出具体的结果，再去思考为什么会出现这样的结果，然后用字母表达式表示出数量关系，最后用具体的数字检验含有字母的数量关系是否正确。这个过程可以转化为学生以后自己探究数学知识的方法，让学生终身受益。二是能给解题带来方便。学生可能不理解建立数学模型的意义，但是他们经历了从生活原型中抽象成数学模型、利用数学模型探究数学问题的全过程，在运用过程中能够体会到数学模型给解决问题带来的便利，感受到数学再创造的成就感，促进了他们数学核心素养的发展。

总之，教学“图形与几何”领域的内容时，教师要适时渗透模型意识，引导学生经历数学建模的完整过程。在这个过程中，不仅要加深学生对数学模型的理解，更要让学生体会到数学模型的应用价值，促进学生内化和丰富数学模型，而不是简单地套用数学模型解决问题，使学生形成良好的思维习惯和数学品格。