全概率公式及其应用

李文东

(广东省中山市中山纪念中学)

概率论是统计学在现实生活中应用的理论基础，它的特点是推理严谨和逻辑性较强，是学生比较难掌握的学科，尤其是正确应用全概率公式.概率论中的全概率公式是一个重要的公式，它不仅包括了事件的并和互斥的概念，而且包括概率的加法公式、概率的乘法公式以及条件概率公式等，它提供了一条有效的途径来计算复杂事件的概率，通常能使比较复杂事件的概率计算问题得到简化，应用较为广泛.条件概率是人教2004年版高中数学《选修2－3》第二章第二节的内容，全概率公式是人教社2017年A版高中数学选择性《必修3》的内容，全概率公式已经纳入了《普通高中数学课程标准(2017年版2020年修订)》中，2019年全国Ⅰ卷理科第22题间接考查了全概率公式，本文简单介绍全概率公式及其应用.

1 全概率公式

全概率公式:对一个样本空间Ω，设A1，A2，…，An是一组两两互斥的事件，A1∪A2∪…∪An＝Ω，且P(Ai)＞0(i＝1，2，…，n)，则对任一事件B⊆Ω，有

证明如图1所示，B＝(BA1)∪(BA2)∪…∪(BAn)，显然BA1，BA2，…，BAn也两两互斥.

图1

由概率的加法公式和概率的乘法公式得

全概率公式的基本思想:将事件B转化为n个两两互斥的事件之和，即B＝(BA1)∪(BA2)∪…∪(BAn)，其中A1，A2，…，An恰好构成样本空间Ω的一个划分，若我们可以求得条件概率P(B|Ai)(i＝1，2，…，n)，那么用全概率公式即可求得P(B).

例1盒中有黄球3个，蓝球7个，甲先从中任取2个，乙再从其余的8个中任取3个.甲、乙约定，取得黄球多者为胜，求甲胜的概率.

分析显然乙取出的黄球的个数受到甲取出的黄球个数的影响，分两步进行:第一步，看甲先取出的黄球个数，可能是0个，可能是1个，也可能是2个，我们分别把它们设为事件A0，A1，A2，显然A0，A1，A2两两互斥，且P(Ai)＞0(i＝0，1，2)，A0∪A1∪A2＝Ω;第二步，看乙取出黄球的个数，比较甲、乙两人谁取的黄球多，这类问题需要用全概率公式求解.

解设事件B:“甲取出的黄球比乙的多，甲胜”，A0:“甲取出的黄球个数为0个”，A1:“甲取出的黄球个数为1个”，A2:“甲取出的黄球个数为2个”.由题意可知

则由全概率公式可得

2 全概率公式在递推数列中的应用

在一些复杂的概率计算问题中，特别是涉及概率序列时，可以利用全概率公式得到概率序列的递推关系式，这是解决这类问题的难点.

例2某个质地均匀的正四面体玩具的4个面上分别标有数字0，1，2，3，将这个玩具抛掷n次，记第n次抛掷后玩具与桌面接触的面上所标的数字为an，数列{an}的前n项和为Sn.记Sn是3的倍数的概率为P(n).

(1)求P(1)，P(2);

(2)求P(n).

分析本例要求第n次抛掷后Sn是3的倍数的概率P(n)，概率与次数有关，这类问题需要利用全概率公式建立P(n)的递推关系，将概率问题转化为数列问题求解.由题意，Sn的结果有:“Sn为3的倍数”“Sn除以3的余数为1”“Sn除以3的余数为2”这3种，显然这3种结果所代表的事件是两两互斥的，而第n＋1次抛掷后的结果Sn＋1与an＋1，第n次抛掷后的结果Sn有关，即Sn＋1＝Sn＋an＋1，当Sn为3的倍数时，an＋1取值为0或3，则Sn＋1也为3的倍数;当Sn除以3的余数为1时，an＋1取值为2，则Sn＋1也为3的倍数;当Sn除以3的余数为2时，an＋1取值为1，则Sn＋1也为3的倍数;再利用全概率公式，可得到P(n)的递推关系式.

解(1)由题意，P(1)代表抛掷1次后，S1＝a1为3的倍数的概率.抛掷1次，一共有4种结果，出现0和3时符合要求，故同理，抛掷2次，一共有42＝16种结果，出现1＋2，2＋1，0＋0，3＋3，0＋3，3＋0时，符合要求，共计6种情况，故

(2)设An，Bn，Cn分别表示第n次抛掷后“Sn是3的倍数”“Sn除以3的余数为1”“Sn除以3的余数为2”，Sn除以3的余数为1的概率为P1(n)，Sn除以3的余数为2的概率为P2(n)，即P(n)＝P(An)，P1(n)＝P(Bn)，P2(n)＝P(Cn)，显然An，Bn，Cn两两互斥，且由全概率公式

注:也可以利用对立事件的全概率公式求解，由全概率公式有

例3一种掷骰子走跳棋的游戏如下:棋盘上标有第0站、第1站、第2站……第100站，共101站，设棋子跳到第n站的概率为Pn，一枚棋子开始在第0站，棋手每掷1次骰子，棋子向前跳动1次.若掷出奇数点，棋子向前跳1站;若掷出偶数点，棋子向前跳2站，直到棋子跳到第99站(获胜)或第100站(失败)时，游戏结束(骰子是用一种均匀材料做成的立方体形状的游戏玩具，它的6个面分别标有点数1，2，3，4，5，6).

(1)求P0，P1，P2;

(2)求该游戏获胜的概率.

分析第(2)问求该游戏获胜的概率，即棋子跳到第99站的概率，显然直接计算这个概率很复杂，需要通过全概率公式建立Pn的递推关系式来求解.由题意，当棋子跳到第n(n≥2)站时，它与上一次棋子所处的站点和掷骰子出现的点数有关.即棋子跳到第n(n≥2)站，它包含棋子跳到第n－1站的条件下且掷骰子出现的点数为奇数和棋子跳到第n－2站的条件下且掷骰子出现的点数为偶数这两种情形，因此引入互斥事件:Ai表示“棋子跳到第i站”，可以通过全概率公式建立Pn的递推关系式.

解(1)棋子开始在第0站是必然事件，所以P0＝1.

棋子跳到第1站，只有一种情形，第一次掷骰子出现奇数点，其概率为

棋子跳到第2站，包括两种情形，即第一次掷骰子出现偶数点，其概率为前两次掷骰子出现奇数点，其概率为

(2)设事件Ai表示“棋子跳到第i站”，则棋子跳到第i站的概率为Pi＝P(Ai)(i＝1，2，…，n)，显然A1，A2，…，An两 两 互 斥，且A1∪A2∪…∪An＝Ω，又

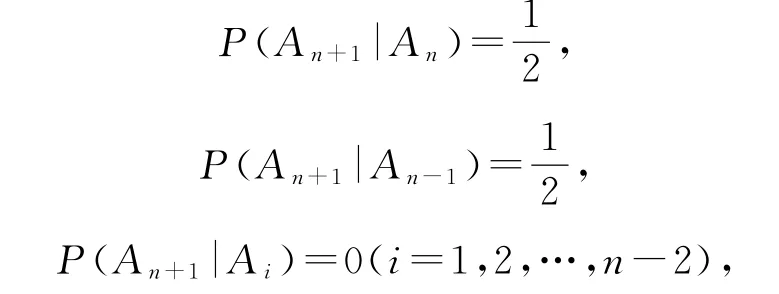
由全概率公式:

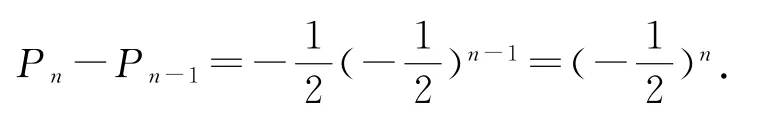
所以

例4(2019年全国Ⅰ卷理22)为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定:对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得－1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得－1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

(1)求X的分布列;

(2)若甲药、乙药在试验开始时都赋予4分，pi(i＝0，1，…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0＝0，p8＝1，pi＝api－1＋bpi＋cpi＋1(i＝1，2，…，7)，其中a＝P(X＝－1)，b＝P(X＝0)，c＝P(X＝1).假 设α＝0.5，β＝0.8.

(ⅰ)证明:{pi＋1－pi}(i＝0，1，2，…，7)为等比数列;

(ⅱ)求p4，并根据p4的值解释这种试验方案的合理性.

分析本题作为2019年高考数学压轴题，难点在于读懂题意，出题者为了降低难度，直接给出了递推式pi＝api－1＋bpi＋cpi＋1，这里我们重点分析该式的推导过程.由题意，甲药和乙药累计得分之和为8分，若最终认为甲药比乙药更有效，则最终甲药累计得分为8分，由于pi(i＝0，1，…，8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，也就是甲药的累计得分为i时，最终甲药累计得分为8分的概率.设A，B，C分别表示事件:一轮实验中“施以甲药的白鼠治愈且施以乙药的白鼠未治愈”“施以乙药的白鼠治愈且施以甲药的白鼠未治愈”“都治愈或都未治愈”，则A，B，C两两互斥且A∪B∪C＝Ω，P(A)＝P(X＝1)＝α(1－β)，P(B)＝P(X＝－1)＝(1－α)β，P(C)＝P(X＝0)＝αβ＋(1－α)(1－β)，M表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”，由全概率公式P(M)＝P(A)P(M|A)＋P(B)P(M|B)＋P(C)P(M|C)，其中P(M|A)表示在甲药的累计得分为i时第一轮试验中施以甲药的白鼠治愈且施以乙药的白鼠未治愈的条件下，最终认为甲药比乙药更有效的概率，此时甲药的累计得分为i＋1分，故P(M|A)＝pi＋1，同理P(M|B)＝pi－1，P(M|C)＝pi，于是pi＝api－1＋bpi＋cpi＋1＝α(1－β)pi＋1＋[αβ＋(1－α)(1－β)]pi＋(1－α)βpi－1.

解(1)由题意可知X所有可能的取值为－1，0，1，所以P(X＝－1)＝(1－α)β，P(X＝0)＝αβ＋(1－α)(1－β)，P(X＝1)＝α(1－β)，则X的分布列如表1所示.

表1

(2)因为α＝0.5，β＝0.8，所以a＝0.5×0.8＝0.4，b＝0.5×0.8＋0.5×0.2＝0.5，c＝0.5×0.2＝0.1.

(ⅰ)因为pi＝api－1＋bpi＋cpi＋1(i＝1，2，…，7)，即pi＝0.4pi－1＋0.5pi＋0.1pi＋1(i＝1，2，…，7)，整理得5pi＝4pi－1＋pi＋1(i＝1，2，…，7)，pi＋1－pi＝4(pi－pi－1)(i＝1，2，…，7)，所以{pi＋1－pi}(i＝0，1，2，…，7)是以p1－p0为首项，4为公比的等比数列.

p4表示最终认为甲药更有效的概率.由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8时，认为甲药更有效的概率为此时得出错误结论的概率非常小，说明这种试验方案合理.

对于一些比较复杂的计数问题，我们也借助全概率公式来求解，下面举例说明.

例5甲、乙、丙三个人相互传球，由甲开始发球，并作为第一次传球，经过n次传球后，球又回到甲手中，则不同的传球方法有多少种?

分析本题是经典的传球问题，显然每次传球都是随机的，即每次有两种传球方式，n次传球后，总的传球方式为2n种.设经过第n次传球后，球在甲手中的不同方法有an种，则第n次传球后球又回到甲手中的概率为第n次传球后球共有“球又回到甲手中”“球又回到乙手中”“球又回到丙手中”这3种结果，它们所代表的事件是两两互斥的，因此可以利用全概率公式建立an的递推关系式求解问题.

解设An，Bn，Cn分别表示第n次传球后“球又回到甲手中”“球又回到乙手中”“球又回到丙手中”，其概 率 分 别 为p(n)＝P(An)，q(n)＝P(Bn)，r(n)＝P(Cn)，显 然An，Bn，Cn两 两 互 斥 且An∪Bn∪Cn＝Ω，则由全概率公式

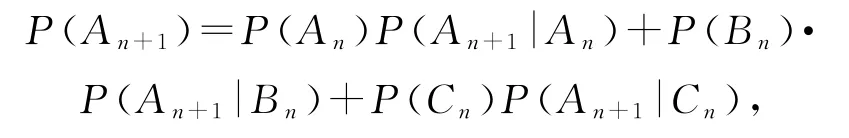
即

设经过n次传球后，球分别在甲、乙、丙手中的不同方法有an，bn，cn种，且有a1＝0，经过n次传球后共有2n种不同的传球方法，故an＋bn＋cn＝2n，代入式①得an＋1＝bn＋cn，从而an＋an＋1＝2n，由此可得

从以上问题可以看出，当涉及复杂的概率计算特别是事件在相关联的不同状态下的概率问题时，可以通过全概率公式找到相关联事件概率之间的关系来求解.