A100钢的热变形行为及加工图
张一帆,朱晓飞,周舸,和正华,张浩宇,陈立佳,王瑞春
A100钢的热变形行为及加工图
张一帆1,朱晓飞1,周舸1,和正华1,张浩宇1,陈立佳1,王瑞春2
(1. 沈阳工业大学 材料科学与工程学院,沈阳 110870;2. 潍坊科技学院 智能制造学院,山东 寿光 262700)
研究A100钢的热变形行为,确定热加工范围并优化工艺参数。使用Gleeble-3800热模拟实验机,对A100钢进行应变为0.6,变形温度为1073~1473 K,应变速率为0.01~10 s–1的等温热压缩实验。利用A100钢的热压缩实验数据,建立在不同变形温度、不同应变速率下的真应力-真应变曲线。建立A100钢基于唯象的本构模型与基于物理的本构模型以及基于Murty失稳准则的热加工图。当应变速率一定,温度升高或一定,应变速率下降时,A100钢的流变应力会减小,流变应力曲线上主要表现为动态再结晶的软化机制。构建的基于唯象的本构方程可以对A100钢在应变为0.6时的流变应力进行较好的预测,基于物理的本构方程可以反映出A100钢的物理特性,通过构建的基于Murty失稳准则的加工图可以得到A100钢的加工范围是温度为1173~1223 K,应变速率为0.01~0.1 s–1和温度为1323~1373 K,应变速率为0.05~ 0.15 s–1时。
A100钢;热变形;本构模型;加工图
近年来随着飞机行业的不断发展,对飞机上主要承受载荷的构件尤其是起落架在综合性能方面的要求也在不断提高。A100钢在经过热处理后,不仅抗拉强度可以达到1930 MPa以上,而且断裂韧性也可以同时达到110 MPa·m1/2以上,具有优良的综合力学性能,现在已经应用在部分飞机的起落架上[1-3]。在飞机上像起落架这种大型构件,通常是先用锻造的方法生产出整个构件的坯料,随后对坯料采用机械加工的方法进行精加工,在热加工过程中易产生偏析、晶粒粗大、流变失稳等问题[4]。任书杰等[5]对A100钢的流变应力曲线分别进行了摩擦力和温度的修正,构建了基于唯象的本构模型,具有较好的预测能力。YUAN等[6]通过对比A100钢的JC本构模型以及改进后的JC本构模型,发现改进后的JC本构模型是最佳的选择。任书杰等[7]对A100钢的动态再结晶行为进行研究,建立了晶粒大小的预测模型,预测的数值大小与实验结果匹配的效果较好。苗小浦等[8]通过研究发现A100钢在1193~1353 K发生热变形时,可以观察到明显的动态再结晶现象。
合理的热加工工艺可以改善组织性能,减少偏析,还可以通过动态再结晶而改善晶粒大小。对A100钢在不同应变速率和不同温度下进行热压缩实验,建立不同条件下A100钢的真应力-应变曲线,通过曲线可以直观地反映出流变应力的变化趋势,并对热变形的过程进行预测,进而构建加工图。基于热加工图可以设计A100钢的合理热加工范围和工艺参数,获得组织均匀,性能良好的产品。
1 实验
材料为A100钢,牌号为23Co14Ni11Cr3Mo[9]。在热压缩实验开始前,需要先将锻态的A100钢母材利用线切割的方法加工成高度为1.2 cm,半径为0.4 cm的小圆柱。采用Gleeble-3800热模拟实验机进行热压缩模拟实验,首先是用真空感应加热方式进行升温,将加热速度设置为10 ℃/s,当加热到事先设定好的实验温度后,需要保温5 min,以此使A100钢试样内部与外部表面的温度趋于一致。实验时应该在圆柱状试样的两端适当添加润滑剂,减少试样两端与机器之间的摩擦力,减轻因为摩擦力而出现的试样中间鼓起的程度。热压缩的温度为1073~1473 K,应变速率为0.01~10 s–1,应变控制在0.6。在温度分别为1073,1173,1273,1373,1473 K,应变速率分别为0.01,0.1,1,10 s–1时,绘制真应力-应变曲线并建立相关本构模型。
2 结果与分析
2.1 真应力-应变曲线
A100钢在不同热压缩条件下的真应力-应变曲线如图1所示。可以看出,流变应力会随着热压缩时变形温度的变化和应变速率的变化发生显著变化。从整体上看,当热压缩的温度固定时,流变应力会随着应变速率的升高而升高。当热压缩的应变速率固定时,流变应力会随着温度的升高而降低。具体来看,在刚开始变形时,应力会因为应变的增加而快速上升,这是因为在热压缩过程中,随着变形程度的增加发生了加工硬化。在增长到一定程度时,有的曲线上应力会随着应变的增加也增加,但是增加的速度变慢,例如图1a中当应变速率为0.1 s–1时,这是因为动态回复造成的软化作用有限。有的曲线上应力在增加到顶点后,随着应变的增加逐渐趋于平稳,例如图1c中当应变速率为0.1 s–1时,这是因为在试样内部出现了动态回复,动态回复造成的软化作用和材料变形造成的硬化作用基本是差不多可以相互抵消的状态。有的曲线上应力在到达最高点后会缓慢降低,例如图1e中当应变速率为0.01 s–1时,造成下降的原因是试样内部出现了动态再结晶,动态再结晶所造成的动态软化效果已经超过了加工硬化的效果,使应力逐渐缓慢下降。

图1 A100钢在不同条件下的真应力-应变曲线
2.2 本构模型
2.2.1 基于唯象的本构模型
构建A100钢热压缩时的本构方程,可以表达出热压缩过程中流变应力随着温度与应变速率的变化情况,从而可以对热变形的过程进行预测。目前,使用最广泛的是Arrhenius型双曲正弦函数本构模型,已经在多种合金中得到了应用[10],该方程表达式为[11]:









热变形激活能值可以通过式(7)得到,因为在热压缩的过程中,当温度固定不变,应变速率也恒定时,热变形激活能的值是可以看做固定的,根据式(3)可以得到:
微课是以互联网为平台进行教学的一种教学模式,具有短小精悍、突出重点的优势。以“统计分析”为例,教师可采用以下方法教学:首先,于课前为学生拍摄微课视频。视频的内容应包括“定义工资项目计算公式”,以及“设置所得税参数”等。视频制作完成后,需经QQ或E-mail,将视频发送给学生,要求其观看,并给予教师反馈。其次,课上教师应鼓励学生,说出针对微课知识所存在的疑问,而教师则应帮助学生解答问题。采用上述方法教学,能够提高课堂教学效率,且能够将课堂时间更多的留给学生进行讨论。长远来看,对会计电算化课程氛围的改善以及教学质量的提高具有积极意义。


将峰值应力代入式(8),以ln[sinh]为轴,1000/为轴,绘制线性回归后的关系曲线,如图2d所示。通过计算经线性回归后的曲线的斜率为10.0589。将图2c和图2d中的斜率代入式(7),可以求出热变形激活能=363 789.1715 J/mol。通过式(9)可以计算出ln=32.9901,则=2.1259×1014。将参数带入式(3)可以得到A100钢在应变为0.6时基于唯象的本构方程为:

为了表现出热压缩时的温度和应变速率对A100钢热变形行为的影响,引入一个温度补偿应变速率因子参数(Zener-Holloman参数):

对式(11)两边取对数可以得到:




图2 流变应力与不同变量之间的拟合关系

图3 ln Z-ln[sinh ασ]关系
对式(13)进行误差分析,将计算所得的峰值流变应力作为轴,将实验所得的峰值流变应力作为轴,可以得到图4,其中相关性=0.9718,平均相对误差AARE=4.6459%,说明相关性比较强,该本构模型可以对A100钢在应变为0.6时的流变应力进行预测。
2.2.2 基于物理的本构模型
建立A100钢基于物理的热变形本构模型,不仅可以反映A100钢在热压缩过程中流变应力的变化,还考虑了热压缩的温度对于弹性模量以及自扩散系数的影响,反映了A100钢的物理特性,其中(),()表达式为:




式(18)为幂函数方程的形式,式(19)为指数函数方程的形式,式(20)为双曲正弦函数方程的形式:


(20)

2.3 热加工图
2.3.1 热加工图的失稳判据
动态材料模型(DMM)是由Prasad和Gegel首先在20世纪80年代提出的[13],在多种合金中都得到了应用[14-16]。根据动态材料模型(DMM)的理论,在热压缩实验中,可以将发生热塑性变形的整个过程视为一个能量耗散系统。材料在热塑性变形过程中吸收的总能量为,主要由2种能量构成,其中一种称为能量耗散量,是材料发生变形所需要消耗掉的能量,另一部分称为能量耗散协量,是材料变形时组织发生了改变所耗散的能量。A100钢在热压缩时的能量耗散与分配可以表示为:

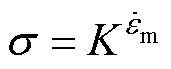

A100钢在应变为0.6时,如果变形温度也恒定,则有:

当=1时,因为此时材料能量耗散的状态是线性的,是比较理想的状态,此时的值恰好为/2,即达到最大值,所以能量耗散系数就可以写为:



系统不稳定,容易发生失稳,此时的失稳准则为:
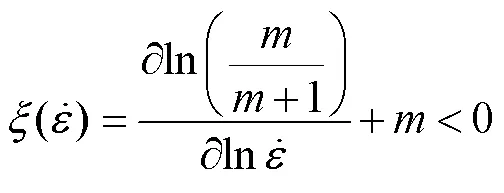
Murty等指出应变速率敏感性指数可能不是常数,有可能在应变速率改变时而随之变化[18],的值应该表示为:

此时的失稳准则为:

2.3.2 热加工图
构建A100钢在应变为0.6的热加工图,需要先构建出对应的能量耗散图以及流变失稳图,以及计算出相关的能量耗散参数、流变失稳参数。根据式(28)可以求出能量耗散参数,能量耗散图就是在应变为0.6时,当温度不同,应变速率发生变化时,能量耗散参数随之发生变化的曲线图,如图6a所示。根据式(29)可以求出流变失稳参数,流变失稳图就是在应变为0.6时,当温度不同,应变速率发生变化时,流变失稳参数随之发生变化的曲线图,如图6b所示。将2个图叠加起来,即可得到A100钢在应变为0.6的热加工图。图6c中阴影灰色的部分是会发生流变失稳的区域,空白的部分为不会发生流变失稳的区域。一般情况下,能量耗散参数越小越容易失稳。能量耗散参数越大材料的塑性越好,越有可能发生动态再结晶,较为适合在这样的区域进行热加工,从图6c可以看出,A100钢的失稳区域主要分布在应变速率较大的区域内,温度越低,失稳的区域会越大。还可以看出,当应变速率为0.01 s–1,温度为1143~ 1243 K时,以及当应变速率为0.1 s–1,温度为1273~ 1373 K时,能量耗散的数值较大,材料的塑性较好,可以在这个区域下进行A100钢热加工。

图6 A100钢在应变为0.6的加工图
3 结论
1)A100钢在热变形时,当变形温度增加时或应变速率减小时,流变应力会减小;动态软化的机制主要是动态再结晶。
2)建立了A100钢在应变为0.6时,基于唯象的本构模型,同时在本构方程中加入了参数,表征了热压缩时的温度和应变速率对A100钢热变形行为的影响,并将用含参数的公式表达,对其进行了误差分析,得到相关性=0.9718,平均相对误差AARE= 4.6459%,说明该本构模型可以较好预测A100钢的热变形行为。还建立了基于物理的本构模型,考虑了A100钢的相关物理参数以及0和0受温度变化的影响,反映出了A100钢的物理特性。
3)根据DMM理论,建立了A100钢在应变为0.6时,基于Murty失稳判据下的加工图,得到A100钢较适宜热加工的区域范围为温度为1173~1223 K、应变速率为0.01 s–1和在1323~1373 K、应变速率为0.1 s–1时,应尽量避免在应变速率大的区域加工。
[1] 冯永. 回火工艺对AerMet100超高强钢组织与力学性能的影响[J]. 热加工工艺, 2020, 49(22): 147-149.
FENG Yong. Effects of Tempering Process on Microstructure and Mechanical Properties of AerMet100 Ultra High Strength Steel[J]. Hot Working Technology, 2020, 49(22): 147-149.
[2] ZENG Hao-hao, YAN Rong, WANG Wei, et al. Analytical Modeling of the Heat-Affected Zone in Laser-Assisted Milling of AerMet100 Steel[J]. The International Journal of Advanced Manufacturing Technology, 2020, 109(9/10/11/12): 2481-2490.
[3] 胡愈刚, 王晓平, 周亮, 等. A-100钢材料起落架关键结构件车铣加工工艺研究[J]. 航空制造技术, 2014(8): 83-85.
HU Yu-gang, WANG Xiao-ping, ZHOU Liang, et al. Process Study of Milling for Landing Gear's Key Structures Made of A-100 Steel[J]. Aeronautical Manufacturing Technology, 2014(8): 83-85.
[4] 于梦晓, 李佳, 李卓, 等. 热处理对激光增材制造AerMet100超高强度钢动态力学性能的影响[J]. 中国激光, 2020, 47(11): 62-70.
YU Meng-xiao, LI Jia, LI Zhuo, et al. Effect of Heat Treatment on Dynamic Mechanical Properties of AerMet100 Ultra-High Strength Steel by Laser Additive Manufacturing[J]. Chinese Journal of Lasers, 2020, 47 (11): 62-70.
[5] 任书杰, 罗飞, 田野, 等. A100超高强度钢的流变应力曲线修正与唯象本构关系[J]. 材料工程, 2019, 47 (6): 144-151.
REN Shu-jie, LUO Fei, TIAN Ye, et al. Flow Stress Curve Correction and Phenomenological Constitutive Relationship of A100 Ultra-High Strength Steel[J]. Journal of Materials Engineering, 2019, 47(6): 144-151.
[6] YUAN Z W, LI F G, JI G L. A Modified Johnson Cook Constitutive Model for Aermet 100 at Elevated Temperatures[J]. High Temperature Materials and Processes, 2018, 37(2): 1-10.
[7] 任书杰, 罗飞, 田野, 等. A100超高强度钢的动态再结晶行为及组织演变研究[J]. 塑性工程学报, 2018(4): 149-157.
REN Shu-jie, LUO Fei, TIAN Ye, et al. Research on Dynamic Recrystallization Behavior and Microstructure Evolution of A100 Ultra-High Strength Steel[J]. Journal of Plasticity Engineering, 2018, 25(4): 149-157.
[8] RAN Xian-zhe, ZHANG Shu-quan, LIU Dong, et al. Role of Microstructural Characteristics in Combination of Strength and Fracture Toughness of Laser Additively Manufactured Ultrahigh-Strength AerMet100 Steel[J]. Metallurgical and Materials Transactions A, 2021, 52(4):1248-1259.
[9] 苗小浦, 赵张龙, 孙朝远, 等. Aermet100钢高温变形动态再结晶晶粒演变行为[J]. 精密成形工程, 2016, 8(3): 11-14.
MIAO Xiao-pu, ZHAO Zhang-long, SUN Chao-yuan, et al. High Temperature Deformation Behavior of Dynamic Recrystallization Grains Evolution in Aermet100 Steel[J]. Journal of Netshap Forming Engineering, 2016, 8(3): 11-14.
[10] WANG W, MA R, LI L P, et al. Constitutive Analysis and Dynamic Recrystallization Behavior of As-Cast 40CrNiMo Alloy Steel during Isothermal Compression[J]. Journal of Materials Research and Technology, 2020, 9(2): 1929-1940.
[11] 胡家齐, 王长军, 杨哲, 等. AM355不锈钢的热变形行为[J]. 金属热处理, 2020, 45(3): 50-59.
HU Jia-qi, WANG Chang-jun, YANG Zhe, et al. Hot Deformation Behaviors of AM355 Stainless Steel[J]. Heat Treatment of Metals, 2020, 45(3): 50-59.
[12] 柴传国, 冯雪磊, 武海军, 等. AerMet100钢动态剪切性能数值仿真研究[J]. 北京理工大学学报, 2014, 34(12): 1223-1228.
CHAI Chuan-guo, FENG Xue-lei, WU Hai-jun, et al. Numerical Simulation of Dynamic Shear Properties of AerMet100 Steel[J]. Transactions of Beijing Institute of Technology, 2014, 34(12): 1223-1228.
[13] PRASAD Y V R K, GEGEL H L, DORAIVELU S M, et al. Modeling of Dynamic Material Behavior in Hot Deformation: Forging of Ti-6242[J]. Metallurgical Transactions A, 1984, 15(10): 1883-1892.
[14] LI N, ZHAO C Z, JIANG Z H, et al. Flow Behavior and Processing Maps of High-Strength Low-alloy Steel During Hot Compression[J]. Materials Characterization, 2019, 153: 224-233.
[15] 任书杰, 王克鲁, 鲁世强, 等. TiAl合金的物理本构模型与加工图[J]. 中国有色金属学报, 2020, 30(6): 1289-1296.
REN Shu-jie, WANG Ke-lu, LU Shi-qiang, et al. Physical Constitutive Model and Processing Diagram of TiAl Alloy[J]. The Chinese Journal of Nonferrous Metals, 2020, 30(6): 1289-1296.
[16] KUMAR V A, GUOTA R K, MURTY S V S N, et al. Hot Workability and Microstructure Control in Co20Cr15W10Ni Cobalt-Based Superalloy[J]. Journal of Alloys and Compounds, 2016, 676: 527-541.
[17] SIVAKESAVAM O, PRASAD Y V R K. Characteristics of Superplasticity Domain in the Processing Map for Hot Working of As-Cast Mg-11.5Li-1.5Al Alloy[J]. Materials Science and Engineering: A, 2002, 323(1/2): 270-277.
[18] MURTY S V S N, RAO B N. On the Development of Instability Criteria during Hotworking with Reference to IN 718[J]. Materials Science and Engineering: A, 1998, 254(1/2): 76-82.
Hot Deformation Behavior and Processing Map of A100 Steel
ZHANG Yi-fan1, ZHU Xiao-fei1, ZHOU Ge1, HE Zheng-hua1, ZHANG Hao-yu1, CHEN Li-jia1, WANG Rui-chun2
(1. School of Materials Science and Engineering, Shenyang University of Technology, Shenyang 110870, China; 2. School of Intelligent Manufacturing, Weifang University of Science and Technology, Shouguang 262700, China)
The work aims to study the hot deformation behavior of A100 steel and determine the hot processing range and optimize the process parameters. Gleeble-3800 thermal simulation testing machine was used to carry out an isothermal compression test with a strain of 0.6, a deformation temperature of 1073~1473 K, and a strain rate of 0.01~10 s–1to the A100 steel. The data of hot compression test of A100 steel were adopted to establish the true stress-strain curve at different deformation temperature and different strain rates. Phenomenal-based constitutive model, physical-based constitutive model and hot processing map based on Murty instability criterion were established for A100 steel. When the strain rate was constant, the temperature increased or kept constant. When the strain rate decreased, the flow stress of A100 steel decreased, and the flow stress curve mainly showed the softening mechanism of dynamic recrystallization. The constructed phenomenal-based constitutive equation can better predict the flow stress of A100 steel at a strain of 0.6, and the physical-based constitutive equation can reflect the physical characteristics of A100 steel. Through the constructed processing map based on Murty instability criterion, it can be obtained that the processing range of A100 steel is temperature of 1173~1223 K and strain rate of 0.01~0.1 s–1and temperature of 1323~1373 K and strain rate of 0.05~0.15 s–1.
A100 steel; hot deformation; constitutive model; processing map
10.3969/j.issn.1674-6457.2022.02.014
TG142.41
A
1674-6457(2022)02-0088-07
2021-06-18
张一帆(1997—),男,硕士生,主要研究方向为金属材料及其应用。
朱晓飞(1979—),男,博士,副教授,主要研究方向为微纳尺度材料微观结构与力学性能。

