基于EEMD-SDCCⅠ-HMM的水电机组振动故障识别方法

胡 晓， 肖志怀,2， 刘 东， 赵文利， 王 海， 蒋文君

(1.武汉大学 动力与机械学院，武汉 430072；2.武汉大学 水力机械过渡过程教育部重点实验室，武汉 430072；3.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；4.国家能源集团新疆开都河流域水电开发有限公司，新疆 库尔勒 841000)

随着水电机组复杂化程度和电站智能化水平日益提高，水电机组故障诊断技术也越来越受到重视。故障诊断主要包括信号检测及预处理、故障信号分析及其特征提取、故障类型识别及故障处置决策四大部分[1]。由于水电机组多数故障都在振动信号中有所反映，因此对振动信号进行分析和特征提取是十分必要的[2]。一般情况下，可通过时频分析或图像处理[3]的方法得到故障信号特征，如幅值、频率、相角和轴心轨迹等。当前较为流行的时频分析方法包括小波变换、经验模态分解(empirical mode decomposition，EMD)等。其中，EMD作为一种自适应信号处理方法，避免了小波基和分解层数的选择，被认为是时频分析领域的重大突破[4-5]。然而，当信号间断或受干扰时，EMD分解中常出现模态混叠现象，严重影响信号的后续分析[6]。为此，Wu等[7]提出了集合经验模态分解(ensemble empirical mode decomposirion，EEMD),能够抑制信号分解过程中局部极值在短时间内的频繁跳动，从而解决了因间断事件引起的模态混叠问题。

若故障信号成分复杂或噪声较多，可将时频分析方法与其他检测指标相结合以获取信号中的有效信息，如许多学者采用奇异值、近似熵、样本熵等可以反映信号中某些变化特性的参数作为故障检测指标。得到故障特征后，可结合神经网络、支持向量机和随机森林等分类方法等进行模式识别。然而受模型自身限制，上述方法通常需要将原始振动信号划分成等长的数据片段，把每个片段视为单独的输入向量进行处理，可能忽略了相邻输入向量间的时序关系[8]，造成部分故障信息丢失。隐马尔科夫模型(hidden Markov model，HMM)能够对一个时间跨度上的信息进行统计建模和分类,是一种基于统计学理论的动态模式识别工具，对于非平稳和低重复性的信号，具有很强的模式分类能力。近年来HMM受到研究人员的广泛关注，已经被成功应用于模式识别的众多领域[9]。

为了充分挖掘水电机组振动信号中能反映机组状态的关键特征，本文结合信号处理领域的EEMD和图像识别领域中的编码理论，提出了一种新的水电机组故障特征提取方法。此外，考虑振动信号的时序关系，借助HMM的模式识别功能对编码所得特征向量分类，达到机组故障识别的目的，最后用试验验证了该方法的有效性。

1 水电机组振动信号的IMF特性

1.1 EEMD算法

Huang等通过对白噪声EMD分解的研究，发现EMD分解的作用类似于二进制滤波器，且白噪声的能量在其频谱上呈现均匀分布状态，故提出了基于噪声辅助分析的改进EMD方法，即EEMD。EEMD利用白噪声频谱均匀分布的特性，在待分析信号中加入白噪声来补充一些缺失的尺度，一方面使得不同时间尺度的信号自动映射到合适的参考尺度上去;另一方面，零均值高斯白噪声经过多次平均计算后会相互抵消，于是集成均值的计算结果可视作最终结果，且有效解决了EMD的模态混叠问题。

EEMD算法步骤如下[10]。

步骤1在目标信号x(t)中加入随机白噪声(由噪声等级确定)n(t)，得到待处理信号s(t)

s(t)=n(t)+x(t)

(1)

步骤2对合成信号s(t)进行EMD分解，得到各阶本征模态函数(intrinsic mode functions,IMF)

(2)

式中:m为IMF的个数;ci(t)和rm(t)分别为IMF和残差。

步骤3重复n(n定义为总体平均数)次步骤1和步骤2，每次加入不同的白噪声。

步骤4将得到的各阶IMF的均值作为最终结果。

(3)

研究表明，噪声等级和总体平均数分别取经验值0.2和100时，EEMD分解效果较好[11-12]。此外，在EMD分解中，信号两端点不一定是极值点，直接利用样条函数计算包络线会产生端点效应，使分解结果中出现与信号无关的分量，造成信号失真，故本文在步骤2中采用线性外推法进行端点延拓来抑制端点效应。

1.2 IMF的标准差特性

在现代机械故障诊断领域，频谱分析是常用于判断故障类型的方法，其本质是捕捉信号中特征频率的幅值变化。由EMD的原理可知，EMD分解所得IMF是一系列窄带分量，且每个分量具有不同的频率成分和带宽。同时，当被分解信号存在差异时，其相同阶数的IMF的截止频率和带宽也不相同。由此推断，IMF的特征参数，如标准差(standard deviation，SD)等可以体现出信号中频率成分的变化情况，进而成为判断故障的依据。

为研究IMF的标准差特性，构造如式(4)所示的一般信号，设定采样频率为1 024 Hz，采样时间为1 s。如图1所示,该信号的标准差是幅值(a)、频率(f)和相角(b)的函数。从图1(a)、图1(b)可以看出，标准差的大小由信号幅值决定，不随频率和相角的改变发生变化。在图1(c)中，当幅值为常数0.03时，相角对标准差的影响比频率大，但是标准差的变化范围很小，相比图1(a)、图1(b)可以忽略不计。

(c) 不平衡状态测试样本在各HMM上的输出值

(b) 碰磨状态测试样本在各HMM上的输出值

(a) 正常状态测试样本在各HMM上的输出值

(a) 当b=0时，SD与a和f的关系

y=asin(2πfx+b)

(4)

基于以上分析，进一步研究水电机组振动信号IMF的标准差特性。根据文献[13]可知水电机组振动频率与故障原因及机组参数相关，据此可构建不同故障状态的水电机组振动信号。仿真水电机组参数，机组故障原因与频率成分的关系分别如表1和表2所示。

表1 仿真机组参数表

表2 水电机组故障原因与频率成分关系表

构造该机组4种不同故障状态下含有噪声时的振动仿真信号如式(5)～式(8)所示。其中:A1为尾水管低频涡带引起的振动故障;A2为推力轴瓦不平引起的振动故障;A3为转轮叶片开口不均引起的振动故障;A4为导叶开口不均引起的振动故障。

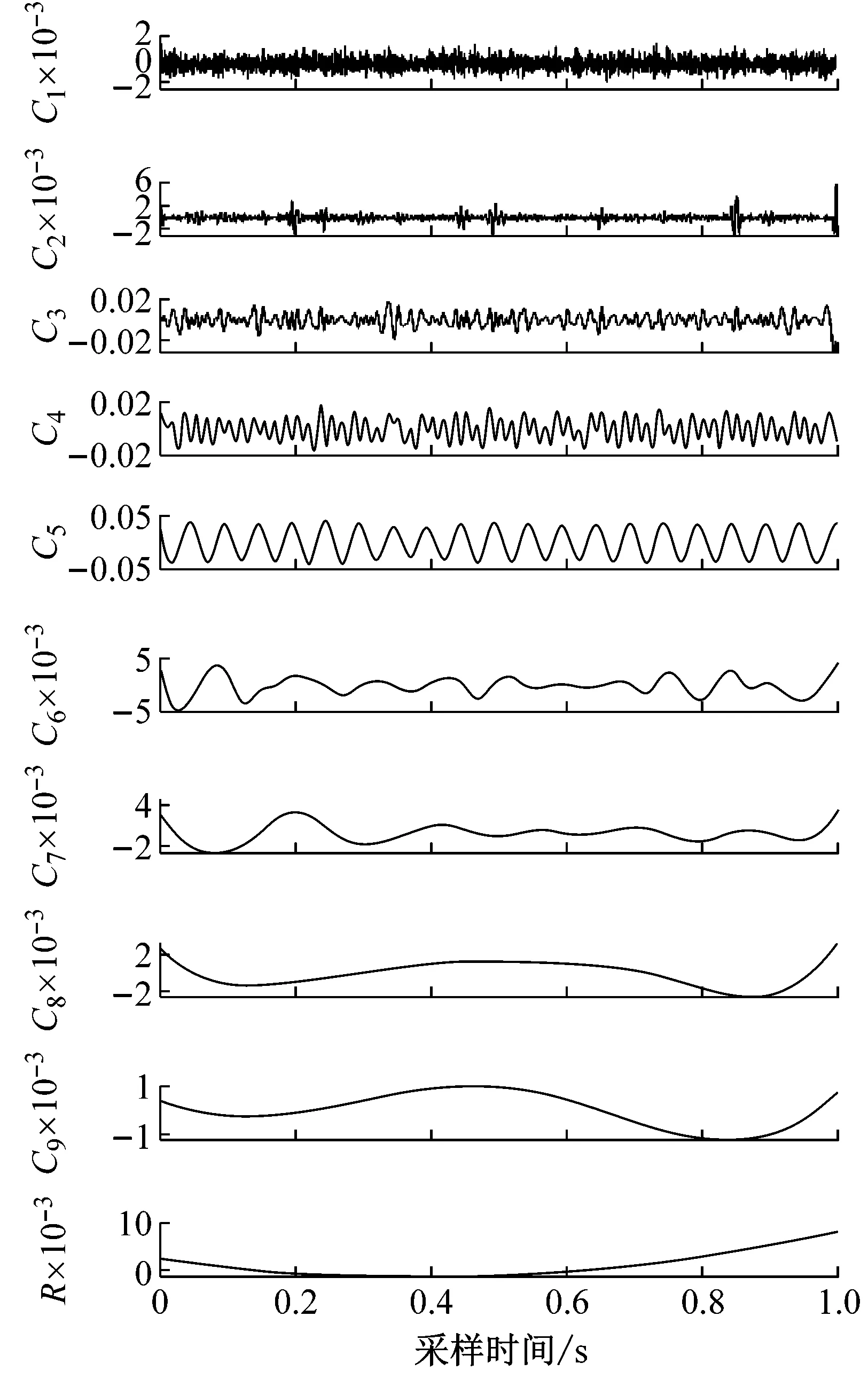
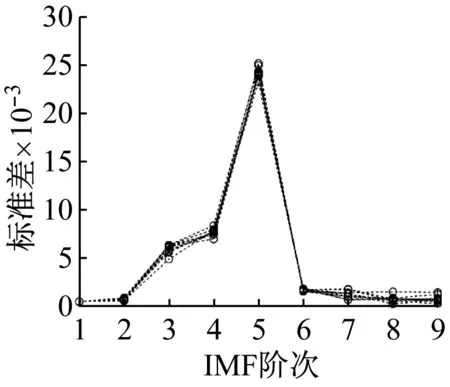
式中:S1(t)，S2(t)，S3(t)，S4(t)为含噪振动仿真信号;b1(t)，b2(t)，b3(t)，b4(t)为高斯白噪声成分。S1(t)，S2(t)，S3(t)，S4(t)的振动波形,如图2所示。应用改进EEMD对其进行10层分解，计算前9阶IMF的标准差得到标准差曲线，如图3所示。

(a) 尾水管低频涡带引起的振动故障

从图3可知，不同故障状态振动信号各阶IMF的标准差和其阶数的关系存在明显差异，可作为区分故障类别的特征参数。

图3 各阶IMF标准差和其阶数的关系曲线

2 隐马尔科夫模型

隐马尔科夫模型(HMM)是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列I=(i1,i2,…,iT)，再由各个状态生成一个观测而产生观测随机序列O=(o1,o2,…,oT)的过程，序列的每一个位置又可以看作是一个时刻[14]。一个HMM通常由以下几个参数来描述：

(1) 马尔科夫链隐状态数N。所有可能状态的集合记为Q={q1,q2,…,qN}。

(2) 在各个隐状态下所有可观测值数M。所有可能观测的集合记为V={v2,v2,…,vM}。

(3) 隐状态间状态转移概率矩阵

A=[aij]N×N,

aij=P(it+1=qj|it=qi),

i=1,2,…,N;j=1,2,…,N

式中，aij为在时刻t处于状态qi的条件下在时刻t+1转移到状态qj的概率。

(4) 观测概率矩阵

B=[bj(k)]N×M,

bj(k)=P(ot=vk|it=qj),

k=1,2,…,M;j=1,2,…,N

式中，bj(k)为在时刻t处于状态qj的条件下生成观测vk的概率。

(5) 初始状态概率分布矢量

πi=P(i1=qi),i=1,2,…,N

式中，πi为时刻t=1处于状态qi的概率。λ=(A,B,π)被称为隐马尔科夫模型的三要素。

3 基于EEMD-SDCCⅠ-HMM的故障识别方法

3.1 HMM模型在故障识别中的应用

HMM应用于设备故障识别的方法可归纳为：首先，对训练数据进行特征提取和标量量化，其次建立具有相应隐状态数和观测值数的HMM，然后利用该模型计算待测数据与训练数据的相似概率，根据相似概率的差异判断信号状态的变化，最终实现模式分类。考虑实际应用需求，本文采用参数少，训练快的离散型隐马尔科夫模型(discrete hidden Markov model，DHMM)，其输入的观测值为离散值，需要对特征向量进行离散化处理，常用的离散化处理方法包括矢量量化和基于Lloyds算法的标量量化等[15-16]。在实际情况中，信号的幅值会因所处环境改变而发生变化，故IMF的标准差幅值也可能随之改变。因此直接使用每个IMF标准差幅值的量化值作为故障特征是不合适的。而标准差曲线的变化趋势包含了由故障机理所决定的信号内在特性，受信号幅值变化的影响很小，可利用编码的方法对趋势进行记忆并以此作为故障特征。基于以上分析，本文提出一种曲线趋势编码(curve trend coding,CC)方式用于将信号IMF分量标准差值离散化。

3.2 标准差曲线趋势编码

由有限点连接而成的曲线，如图3中的标准差曲线，是由多个线段组成的。可以看出，线段有3种趋势：上升、水平和下降。若使用不同的整数(如0，1，2)表示这3种趋势，则按线段排列顺序可得一串数字码，称为该曲线的线码。假设使用0，1，2进行编码，则能写出总计6种不同的编码方式，如表3所示。标准差曲线的每段由一个线码位表示，可通过此方法计算得出图3中标准差曲线相应的线码。

表3 曲线趋势的编码方式

实际中，理想的水平趋势几乎不可能存在。为解决其编码问题，本文引入趋势裕度(trend margin，TM)公式中为MT，放宽水平趋势的判定条件。假设对信号进行EEMD得到m个IMF，当采用编码方式一时，编码方式如图4所示，具体过程如下：

图4 编码方式示意图

(1) 计算标准差曲线最大值和最小值的差值Ad

Ad=max{DS1,…,DSm}-min{DS1,…,DSm}

(9)

(2) 由式(10)所示的判断条件，确定各线码位的值Ci

(10)

此处，MT为常数，由于MT过小时，无意义的平稳趋势可能被判定为上升趋势或下降趋势;而MT过大时，有意义的上升或下降趋势可能被判定为平稳趋势。这两种情况对于特征提取都是不利的，根据经验MT值取0.05～0.20较好。

(3) 将各线码位的值Ci按顺序连接，如式(11)所示。

CC=C1C2…Cm-1

(11)

3.3 编码方式分析

为选出最佳编码方式，利用转子正常、碰磨、不平衡和不对中共4种状态的振动信号进行分析，降噪后的振动信号如图5所示。

(a) 正常

采用EEMD对不同转子状态的振动信号进行10层分解。各状态分解所得IMF,如图6所示。可以看出，IMF的幅值随其阶数的增大呈现出先增大后减小的趋势，其中，正常和碰磨信号的IMF最大幅值均出现在第5阶IMF中，不平衡和不对中信号则出现在第4阶IMF中。计算4种状态各阶IMF的标准差得到对应标准差曲线，图7给出了每种转子状态下的10组IMF标准差曲线。

(a) 正常

由图7可知，同一转子状态的IMF标准差曲线具有相似性，不同转子状态的IMF标准差曲线有较大差异。根据3.2节所述编码方法，用表3中的6种编码方式对图7中4种转子状态对应的IMF标准差曲线进行编码，结果如表4所示。

(a) 正常

表4 不同转子状态的IMF标准差曲线编码

采用欧拉距离(d)来估计任意两条曲线的相似程度，以确定最好的编码方式，计算公式如式(12)所示。

(d) 不对中状态测试样本在各HMM上的输出值

(12)

式中:m为IMF总数;Ci,k和Cj,k分别为样本i和样本j第k个线码位的值。此处在确定各线码位的值时，MT取0.1。图8显示了来源于转子正常，碰磨和不对中状态的3组振动信号IMF标准差曲线，图9显示了两组待测样本的IMF标准差曲线，分别来源于转子碰磨和不对中状态。各样本的IMF标准差如表5所示。加粗的数据表示故障状态与正常状态曲线之间差别较大的部分。

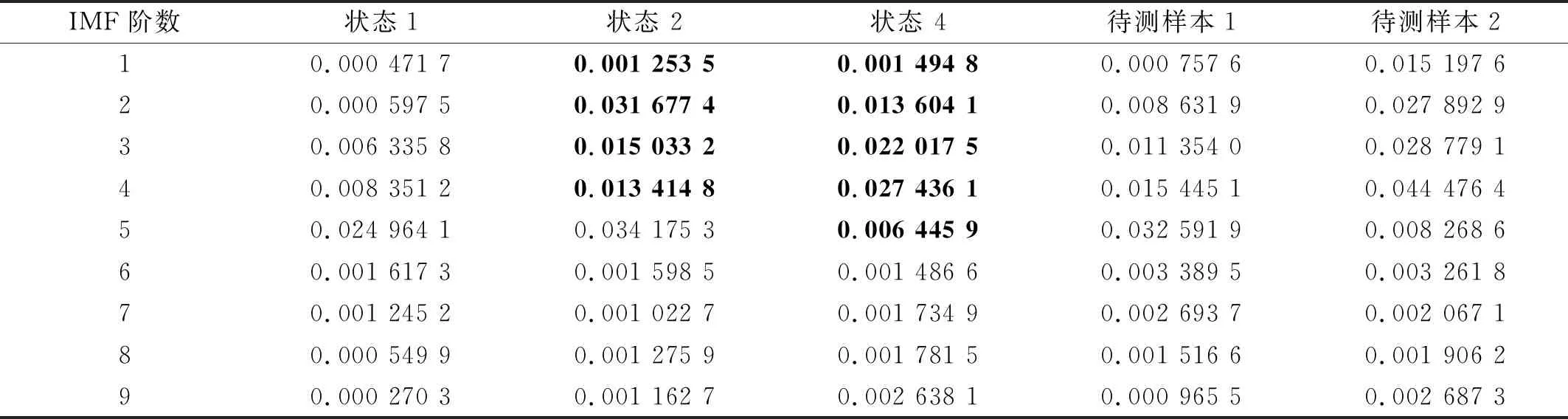
表5 图8和图9中振动信号各阶IMF标准差

(a) 状态1

(a) 待测样本1(属于状态2)

从表5、图7和图8可以看出，转子碰磨和正常的明显区别在于IMF标准差曲线的前3段，即第2～第4阶IMF标准差。转子不对中和正常的明显区别在于IMF标准差曲线的前4段，即第2～第5阶IMF标准差。而图9中待测样本与图8中相同状态样本的标准差曲线也存在差异。由对称性知，编码方式一和六、编码方式二和四、编码方式三和五具有相同的效果，故利用表3中前3种编码方式对图8和图9中信号的IMF标准差曲线进行编码，并计算图9中待测样本与图8中3种样本的欧氏距离，结果如表6所示。

由表6可知:编码方式一对于两个待测样本状态的分类是正确的;而编码方式二无法区分待测样本1是碰磨还是不对中;编码方式三将待测样本1误分类至正常和不对中。尽管3种编码方式对待测样本2的分类都是正确的，但从距离角度看，使用编码方式二、三得到的关于待测样本2和状态4的线码间距离要大于使用编码方式一所得到的对应距离，这表明使用编码方式一对转子正常状态和不对中故障的区分效果最好。

表6 图8和图9中不同IMF标准差曲线的编码结果及距离

综合以上实例可以得出结论：编码方式一在所有编码方式中对于转子故障状态识别效果最好。而从理论上分析，编码方式一应为最理想的编码方式，因为由编码方式一得到曲线上升和下降趋势的线码位与平稳趋势的线码位数值之差即距离相等，编码方式二和三的区别在于前者上升与平稳趋势之间的距离大于下降与平稳趋势之间的距离，后者则相反。因此，之后的分析均采用编码方式一(curve codeⅠ,CCⅠ)对IMF标准差曲线进行编码。

3.4 基于EEMD-SDCCⅠ-HMM的故障识别过程

综合3.2节和3.3节关于IMF标准差曲线趋势编码方式的研究结果,结合HMM在故障识别中的优势,本文提出了基于EEMD-SDCCⅠ-HMM(ensemble empirical mode decomposirion-standard deviation curve codeⅠ-hidden Markov model)的故障识别方法，图10为利用EEMD-SDCCⅠ-HMM进行故障识别的流程，详细说明如下。

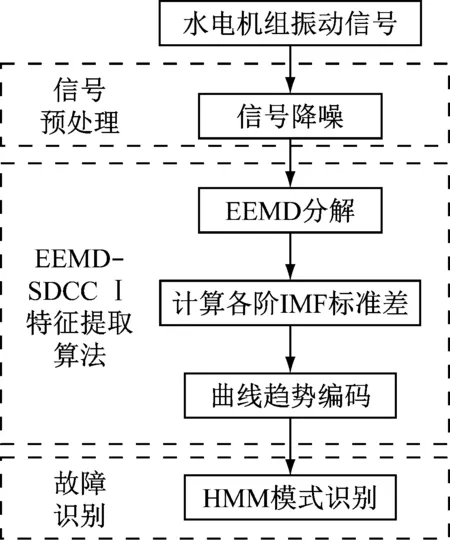
图10 基于EEMD-SDCCⅠ-HMM的故障识别流程

(1) 信号预处理。由于测量环境和机械振动的影响，测量信号中存在较高能量的噪声，为更加充分地提取故障信号中的有效信息，需要在信号分析前对带噪声信号进行一定程度的降噪处理。本文采用小波软阈值降噪去除原始信号中的噪声。

(2) 信号EEMD分解。对降噪后的信号进行EEMD分解得到IMF。

(3) 计算各阶IMF的标准差并编码。计算各阶IMF的标准差，并用3.3节所述CCⅠ编码方式对所有IMF标准差进行编码，将各线码位的值按顺序连接构成特征向量。

(4) 将各状态特征向量输入HMM进行模式识别。将各状态特征向量组成观测序列输入HMM，采用Baum-Welch算法训练各状态HMM[17]，得到模型参数λ=(A,B,π)。模型训练结束后，对于未知状态的数据，提取其特征向量后输入到各HMM中，采用前向-后向算法计算特征向量在各模型下的对数似然概率值，输出概率值最大的模型即为待测数据的原始模型。

4 试验及验证

为了验证基于EEMD-SDCCⅠ-HMM的水电机组故障识别方法的有效性，分别采用转子试验台模拟机组振动信号和水电机组实测振动信号进行试验，并设计了对比试验以说明所提方法的优越性。

4.1 转子振动试验台故障识别(实例一)

图11为本试验所采用的转子试验台系统，转子直径10 mm，长850 mm，安装有两个直径75 mm的转盘，两段转轴经联轴器连接，由4个轴承支撑，另有两个碰摩螺纹箱安装在系统支架上。转子由一台直流电机驱动，用DH5600转速控制器控制其转速。转子振动信号由传感器采集后传输给前置器，进行放大和滤波，最后传入计算机进行存储、显示和分析。利用该试验台分别模拟机组正常状态和碰磨，不平衡，不对中3种机组常见故障。其中，碰摩故障通过将碰摩螺栓旋入碰摩螺纹箱中，使其与转轴接触实现；不平衡故障通过将2 g的质量块旋入转盘边缘处的螺纹孔内实现；不对中故障则通过错置联轴器处两轴的位置实现。

图11 转子试验台系统

采集信号时，设定机组转速为1 200 r/min，采样频率为2 048 Hz。对4种机组状态分别采集100组数据，每组数据包含2 048个点。4种机组状态的振动信号如图12所示。

(a) 正常

对各机组状态振动信号进行预处理，降噪时选择“db8”小波进行3层分解。由于试验数据包含4种机组状态，故需建立4个HMM，分别代表机组正常，碰磨，不平衡和不对中状态。使用K-means聚类方法对经过EEMD-SDCCⅠ算法得到的特征向量聚类，以确定各HMM的隐状态个数，K值由Calinski-Harabaz指数确定。Calinski-Harabaz指数是聚类模型的常见评价指标，其定义如式(13)所示

(13)

式中:N为数据集样本数;k为簇类个数;tr(Bk)，Tr(Wk)分别为簇间散度矩阵和簇内散度矩阵的迹。Bk和Wk的计算公式如式(14)和式(15)所示。tr(Bk)为不同簇间的远离程度，迹越大，不同簇间的远离程度越大;tr(Wk)为同一簇类的密集程度，迹越小，同一簇类的数据集越密集。由以上定义可知，Calinski-Harabaz指数越高，聚类性能越好。

(14)

(15)

式中:nq为簇类q的样本数;cq为簇类q的中心;c为所有数据集的中心;Cq为簇类q的样本集。

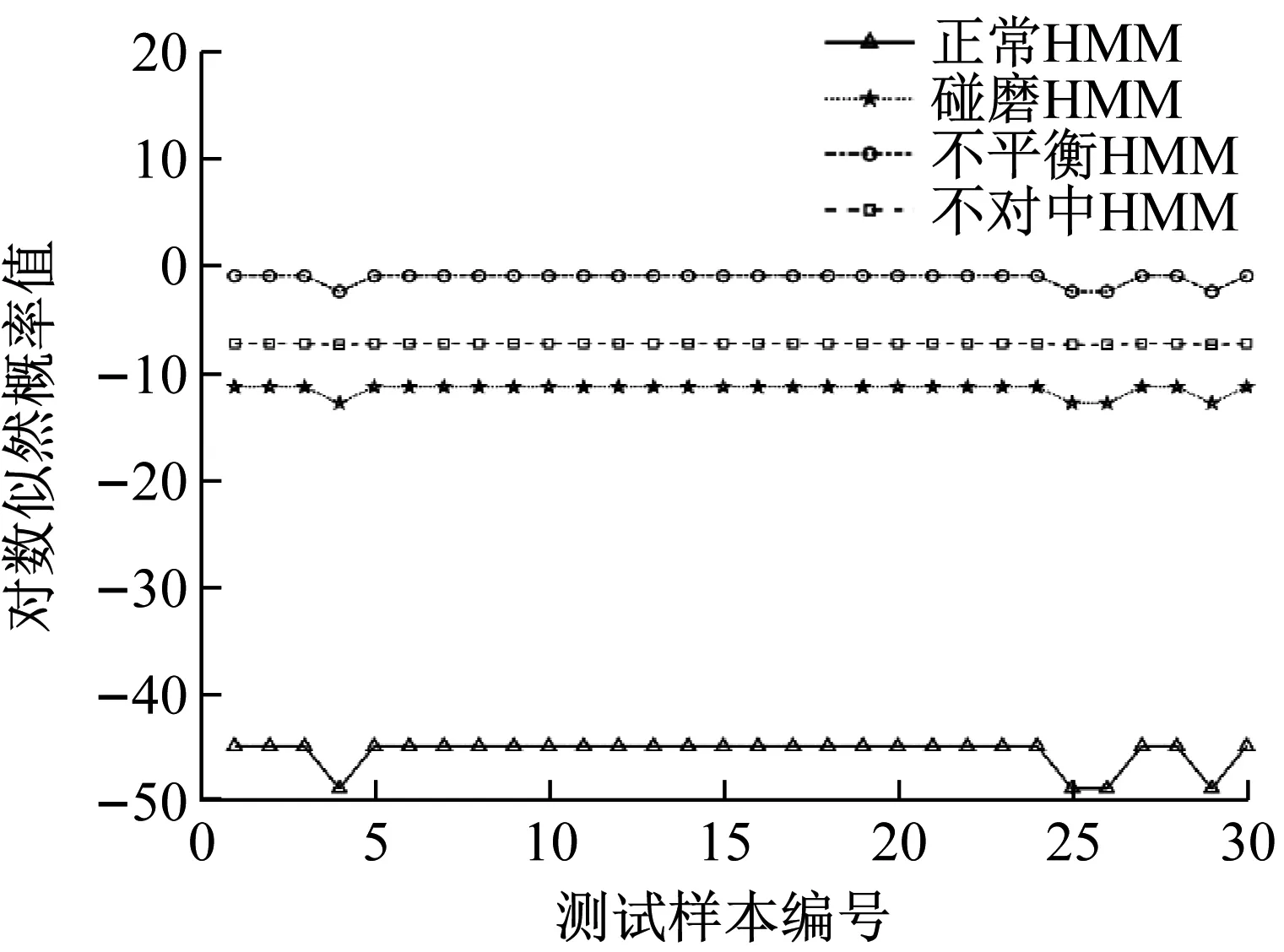
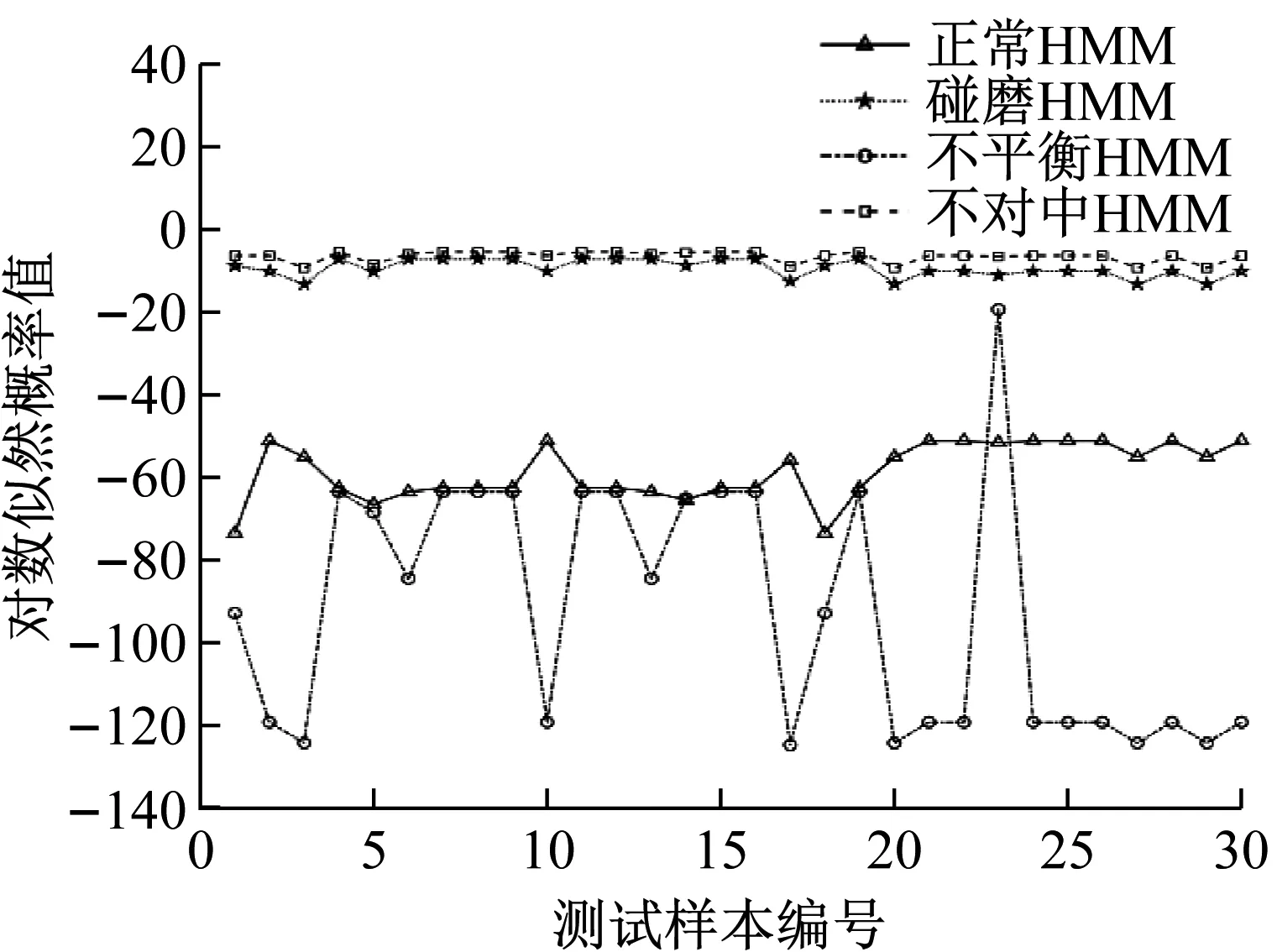
经过试验，确定机组正常，碰磨，不平衡和不对中的隐状态个数分别为6，3，6，3。由于观察矩阵的初值对模型性能影响较大，故在模型训练时采用多次随机初始化，选择得分最高的参数作为模型最佳参数。将4种机组状态前70组IMF标准差线码构成的特征向量作为训练数据，收敛误差设定为1×10-3。4种状态剩余30组IMF标准差线码作为测试数据，输入训练好的各HMM中，得到各HMM输出概率值P(O|λ)，如图13所示。

从图13可以看出，4种机组状态测试样本在各自对应的HMM模型输出概率值最大，分类准确率达到100%，表明EEMD-SDCCⅠ-HMM故障识别模型能有效识别机组正常，碰磨，不平衡和不对中状态，且识别准确率高。

为了对比验证该模型的识别效果，分别采用不同方法对相同的样本进行处理，比较识别结果，如表7所示。其中，编码方式 CCⅡ(curve codeⅡ)表示采用Lloyds算法进行标量量化。VMD-SD-KNN(ariational mode decomposition-standard deviations-k-nearest neighbor)对信号采用VMD分解，分解层数为6层，将信号6阶IMF分量标准差向量输入k近邻分类器(k-nearest neighbor，KNN)进行分类。WT-SampEn-KNN(wavelet transform-sample entropy-k-nearest neighbor)对信号采取小波变换，用MATLAB软件的小波函数wavedec和wrcoef进行分解和重构,小波基函数选择“db3”，分解层数为4层，得到一个小波近似系数和4个小波细节系数，计算各小波系数的样本熵，作为特征向量输入KNN进行分类。

表7 不同故障识别模型对比

将分类器分类类别与原始真实类别一一对应后，采用多分类准确率(P)和多分类召回率(R)评估模型性能。假定原始类别i对应的多分类器输出为i，类别数为K，P和R的计算公式分别如式(16)和式(17)所示。

(16)

(17)

式中:ni为多分类输出的类别为i的样本数量;nii为真实类别为ci且被分类器分类至类别i的的样本数量，即被正确分类的属于类别i的样本数量，njj同理。nij表示真实类别为ci却被分类器分类至类别j的的样本数量，i=1,2，…，K;j=1,2，…，K。为了平衡准确率与召回率的不同影响，采用多分类的F均值作为故障识别模型的综合评价指标。F均值定义如式(18)所示

(18)

当α=1时，F均值又称为准确率与召回率的调和均值，记作F1。

从表7可以看出，在训练样本集和测试样本集相同的情况下，信号分解方法，IMF的特征参数，编码方式和分类模型都会影响故障识别结果。在以上几种故障识别模型中，本文提出的EEMD-SDCCⅠ-HMM模型故障识别效果最佳，达到了100%，即能完全准确地识别机组正常，碰磨，不平衡和不对中状态。此外，对比特征提取所需时间可知， EEMD-SDCCⅠ-HMM模型耗时最短，因此也更有利于实现快速故障识别。

4.2 水电机组故障识别(实例二)

水电机组实测振动信号来源于S水电站的3号机组，水轮机型号为ZZA315-LJ-800，额定功率200 MW。巡检人员发现该机组在运行过程中上机架、水车室、蜗壳以及尾水管等处有明显异常声音，停机检查后发现机组转轮室中环钢板出现脱落，属于水力不平衡故障。事后从电站在线监测系统中获取机组正常运行和发生故障时的轴向振动数据，形成正常状态和故障状态样本各40组，如图14所示。

(a) 正常

各状态前20组数据用于训练，后20组用于测试。采用EEMD-StdCCⅠ计算水电机组实测振动信号的特征向量如表8所示。根据K-means聚类结果确定正常HMM的隐状态数目为4，故障HMM的隐状态数目为2。故障识别结果分别如图15和表9所示。

表8 水电机组实测振动信号特征向量

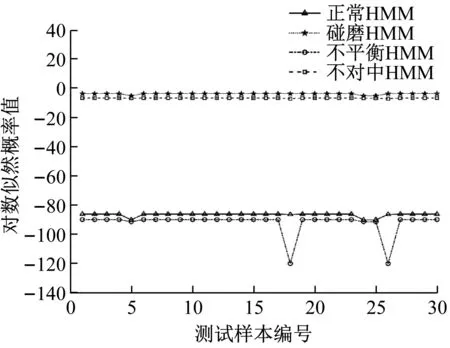
(a) 正常状态测试样本在各HMM上的输出值

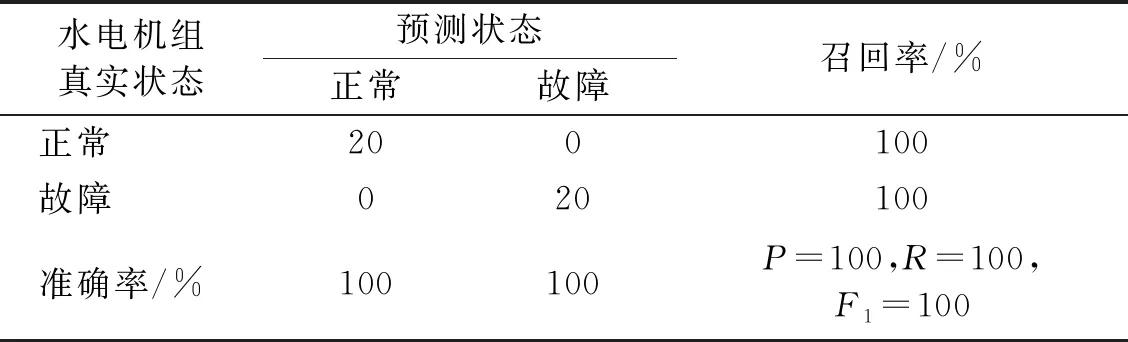
表9 EEMD-SDCCⅠ-HMM对水电机组的故障识别结果

从图15和表9的故障识别结果可以看出，测试样本的预测状态与其真实状态完全一致，表明基于EEMD-SDCCⅠ-HMM的故障识别方法对水电机组状态具有良好的分类性能。

5 结 论

本文提出了基于EEMD和SDCCⅠ的水电机组振动信号特征提取新方法，对水电机组振动信号的IMF标准差特性及曲线编码方式进行了分析，并给出了最佳编码方式。同时，鉴于HMM在模式识别方面的优越性，将其引入水电机组振动故障诊断过程，建立不同机组状态的HMM，实现了机组状态的识别。最后用转子振动信号和水电机组实测振动信号验证了所提方法的有效性，试验结果表明：

(1) 在不同机组状态下采集的振动信号，对其进行EEMD分解后，所得IMF标准差曲线的趋势特征存在差异，可作为机组状态特征向量。

(2) 选择CCⅠ编码方式对IMF标准差曲线的趋势进行编码能够提高状态分类准确率。与其他方法相比，基于EEMD-SDCCⅠ特征提取算法耗时短，得到的特征向量具有稳定性和良好的区分性，结合HMM进行故障识别的准确率较高。

(3) EEMD-SDCCⅠ-HMM是一种有效的水电机组故障识别新方法。随着大数据平台相关技术日趋成熟，获取水电机组故障数据的难度会逐渐降低，本文提出的基于EEMD-SDCCⅠ-HMM的故障识别方法具有敏感型强，模型训练简单的优势，因此可以预见，该方法在水电机组故障诊断领域有很大应用潜力。